Parametric Curve Reconstruction from Point Clouds using Minimization

Techniques

Oscar E. Ruiz

, C. Cort

, M. Aristiz

abal

, Diego A. Acosta

and Carlos A. Vanegas

Laboratorio de CAD/CAM/CAE, Universidad EAFIT, Carrera 49 No 7 Sur - 50, Medell

ın, Colombia

Grupo de Diseo de Productos y Procesos - DPP, Universidad EAFIT, Carrera 49 No 7 Sur - 50, Medell

ın, Colombia

City & Regional Planning, University of California, Berkeley, 228 Wurster Hall #1850, Berkeley, CA 94720-1850, U.S.A.

Keywords:

Parametric Curve Reconstruction, Noisy Point Cloud, Principal Component Analysis, Minimization.

Abstract:

Curve reconstruction from noisy point samples is central to surface reconstruction and therefore to reverse

engineering, medical imaging, etc. Although Piecewise Linear (PL) curve reconstruction plays an important

role, smooth (C

-, C

-,...) curves are needed for many applications. In reconstruction of parametric curves

from noisy point samples there remain unsolved issues such as (1) high computational expenses, (2) presence

of artifacts and outlier curls, (3) erratic behavior of self-intersecting curves, and (4) erratic excursions at

sharp corners. Some of these issues are related to non-Nyquist (i.e. sparse) samples. In response to these

shortcomings, this article reports the minimization-based ﬁtting of parametric curves for noisy point clouds.

Our approach features: (a) Principal Component Analysis (PCA) pre-processing to obtain a topologically

correct approximation of the sampled curve. (b) Numerical, instead of algebraic, calculation of roots in point-

to-curve distances. (c) Penalties for curve excursions by using point cloud to - curve and curve to point cloud.

(d) Objective functions which are economic to minimize. The implemented algorithms successfully deal with

self - intersecting and / or non-Nyquist samples. Ongoing research includes self-tuning of the algorithms and

decimation of the point cloud and the control polygon.

GLOSSARY

PL : Piecewise Linear.

PCA : Principal Component Analysis

: Unknown planar curve to be ﬁt.

S : {p

, p

,..., p

} noisy point sample of C

C(u) : Parametric planar curve approaching C

: {c

,...,c

} PL disjoint curves

approaching local portions of C

L : PL curve, which integrates S

P : [q

,...,q

] Control polygon of C(u).

µ : Stochastic component of S.

: Error of minimization process at

iteration k.

B(p,r) : Disk of radius r centered at p.

Λ(λ) : p + λ. ˆv Parametric line starting at point

p, with direction ˆv and parameter λ.

pca(S

): PCA of point set S

. Returns p, ˆv and

correlation coefﬁcient ρ.

: Residual associated to point p

∈ S

: Point on C(u) closest to cloud point p

d(p,S) : distance from point p to the point set S.

: set of points closest to p

1 INTRODUCTION

A considerable number of applications in CAD,

CAM, Medical Imaging and Geographic Information

Systems, deal with the sectioning of a non-self in-

tersecting shell (a 2-manifold ) in R

with cutting

planes. In Computer Axial Tomography (CAT), Co-

ordinate Measurement Machine (CMM) samples and

Magnetic Resonance Imaging (MRI), data sets (im-

ages, planar wire frames, cross cuts) planar curves

must be recovered from, i.e, noisy unordered point

samples.

Consider a planar curve C

sampled with a point

set S, which includes a stochastic noise with mean µ.

This article presents implemented algorithms to ﬁnd

the b-spline curve C, a parametric approximation for

. The curve C is determined by its control polygon

P. The problem is tackled by tunning control points in

P to minimize f =

∑

i=1

where r

is obtained using

the distances between the cloud points p

∈ S and the

curve C. Besides considering for C

the usual open

smooth curves, this article addresses self-intersecting

and non-Nyquist ones. The method devised includes

E. Ruiz O., Cortés C., Aristizábal M., A. Acosta D. and A. Vanegas C..

Parametric Curve Reconstruction from Point Clouds using Minimization Techniques.

DOI: 10.5220/0004283900350048

In Proceedings of the International Conference on Computer Graphics Theory and Applications and International Conference on Information

Visualization Theory and Applications (GRAPP-2013), pages 35-48

ISBN: 978-989-8565-46-4

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

saddle

point

(a) Saddle Point in 2-manifold M.

(b) Cross Cut at Saddle Point.

1st option: 1- manifold

non 1

- manifold

2nd option: 1- manifold

(d) Self-intersecting C and 1-manifold

Derivations.

Figure 1: Rationale for non-manifold curve reconstruction.

a pre-processing to ﬁnd a topologically faithful initial

guess for P, a re-sample of P to minimize the number

of decision variables, a simpliﬁcation of the calcula-

tion of distance p

to C and a calculation for r

that

includes distances to / from S to C.

1.1 Simple and Self-intersecting Curves

An open curve C : [a,b] ⊂ R → R

is simple if it does

not self - intersect, i.e., C(u

) = C(u

) ⇒ u

= u

for

all u

∈ [a, b].

A typical scenario for self - intersecting curve re-

construction appears when a shell M (Fig. 1(a)), is

cross sectioned by planes. When a plane Π cuts the

shell M the result is a set of (open or closed) planar

curves. In general, those curves do not self - intersect.

However (Fig. 1(b)), if a horizontal plane Π passing

very near or at the saddle point p

cuts M, (nearly) self

- intersecting curves C

are produced. If the curves

are point-sampled, the sampling noise blurs their ex-

act geometry and topology. In such conditions it is

irrelevant whether or not the plane Π exactly contains

the saddle point p

: the point sample indicates a self -

intersecting curve (Fig. 1(c)).

Because of this reason, the recovery of self - in-

tersecting curves is relevant. The algorithms imple-

mented in this article are able to recover a self - in-

tersecting curve C -via its control polygon P- that re-

sembles C

(Fig 1(d), upper). The mutation of C into

1-manifold curve or curves is simple, as shown in the

lower curves in Fig 1(d).

1.2 Non-Nyquist Samples

A fundamental assumption in curve / surface recon-

struction from samples is that the Shannon / Nyquist

principle of digital sampling is respected ((Nyquist,

1928), (Shannon, 1949)). This principle establishes

that the spatial sampling interval δ

cannot be larger

than half of the smallest detail to be reconstructed.

The designer decides which is the size of the physi-

cal detail to reconstruct, and such a decision ﬁxes the

min =

min

Figure 2: Examples of Nyquist / Non-Nyquist Shapes.

sampling interval δ

to use. Fig. 2 presents Nyquist

and non-Nyquist geometries. The left (croissant) one

has a very well deﬁned non-null minimal detail dis-

tance δ

min

. Therefore, the sampling interval δ

can

comply with δ

< δ

min

/2 for a curve reconstruction to

be able to recognize the gorge region. The central ﬁg-

ure (needle), on the contrary, presents δ

min

= 0. The

right ﬁgure (self - intersecting curve) also presents

min

= 0. Therefore, for the center and right geome-

tries the sampling interval must be 0 = δ

< δ

min

/2,

and therefore we would require an inﬁnitely tight

sample if the geometry and topology are to be fully

recovered. The self-intersecting curve (Fig. 2-right)

is obviously a non-manifold one. Notice that non-

manifoldness implies non-Nyquist. The contrary is

not true: a geometry may be manifold and yet non-

Nyquist (Fig. 2-center).

2 LITERATURE REVIEW

The problem of ﬁtting a parametric curve C(u) to a

point cloud S has been addressed by many authors in

recent decades. However, as seen in this section, there

are many open issues in the solutions for such a prob-

lem.

2.1 Objective Function

Eq.1 is the general representation of the objective

function in curve ﬁtting problems. Reference (Fl

ory

and Hofer, 2010) employs ﬁrst order residuals (w = 1)

while references (Wang et al., 2006; Liu et al., 2005;

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

alvez et al., 2007; Liu and Wang, 2008) use second

order residuals (w = 2).

f =

∑

i=1

(1)

Some references ((Wang et al., 2006; Liu et al.,

2005; Fl

ory and Hofer, 2008; Fl

ory and Hofer, 2010;

ory, 2009)) add a smoothing term f

to the objective

function in order to adjust the roughness of the curve:

f =

∑

i=1

+ λ f

. (2)

The term f

contains information on the curve’s

ﬁrst and/or second derivatives and λ determines its

inﬂuence, penalizing large curvatures. Notice that pe-

nalizing the curvature prevents curve ﬁtting for non-

Nyquist samples.

Some authors have explored constrained ap-

proaches. Reference (Fl

ory, 2009) presents con-

strained curve and surface ﬁtting to a set of noisy

points in the presence of regions that the curve or sur-

face must avoid. Reference (Fl

ory and Hofer, 2008)

considers the problem of curves that must lie on a

2-manifold (surface) with forbidden regions. These

procedures are implemented using a constrained non-

linear optimization strategy.

2.2 Distance Measurement

Eq.3 corresponds to the calculation of the distance d

which is usually used in the objective function in Eq.

1 as the residual r

. In curve ﬁtting algorithms norm b

is usually chosen to be b = 2 (i.e., Euclidean distance)

as in (Wang et al., 2006; Liu et al., 2005).

= min

C(u)∈C

C(u) − S

(3)

However, the exact calculation of d

is expensive,

since it is obtained by a minimization procedure at

each ﬁtting iteration. The procedure consists of ﬁnd-

ing the parameter u

which associates a point on the

curve C(u

) with the i-th cloud point p

such that d

a minimum. Namely,

C(u

) − p

= min

C(u)∈C

C(u) − p

(4)

The minimum distance is obtained by performing

an orthogonal projection of the point p

to the curve

C, which occurs when C

) · d

= 0 in Eq. 5.

g(u) =



(u) · (C(u) − p

)



(5)

To sort out this problem, one could solve for u in

g(u) = 0 using Newton’s Method ((Piegl and Tiller,

1997; Liu et al., 2005)), or minimize g(u) using nu-

meric methods ((Wang et al., 2006; Liu and Wang,

2008; Fl

ory and Hofer, 2010; Saux and Daniel, 2003))

or using genetic algorithms ((G

alvez et al., 2007)).

The mentioned approaches have drawbacks inher-

ent to numerical methods, such as the need of a good

initial guess, poor convergence and stagnation at lo-

cal minima. These may lead to poor approximations

of the distance d

yielding unsatisfactory results of the

ﬁtting procedure.

Different methodologies to measure the point-to-

curve distance have been proposed: (i) Point distance,

which preserves the Euclidean distance between the

cloud point and the paired point of the curve ((Wang

et al., 2006; Fl

ory and Hofer, 2008)), (ii) Tangent

distance, which only preserves the distance between

the cloud point and the tangent line projected at the

paired point (Blake and Isard, 1998), and (iii) Squared

distance, which is a curvature-based quadratic ap-

proximation of d

((Wang et al., 2006)). Reference

(Liu and Wang, 2008) presents a comparison of these

methodologies.

It should be noticed that using only point-to-curve

distances to calculate f allows the formation of spuri-

ous curls and outliers (Fig. 8). Because of this reason,

we include also curve-to-point distances in f . This

double estimation allows us to avoid curls and out-

liers.

2.3 Initial Guess

In the present article the term initial guess refers to

a PL or smooth curve which approximates (possibly

with errors) the global point cloud. Numerical opti-

mization strategies require an initial guess to set the

decision variables. This set of values are chosen to

produce a reasonably good value of the function to

optimize, to then start the iterations. A good initial

initial guess has the capacity to offset the difﬁculties

posed by non-convex functions. If the initial guess

falls in a neighborhood in which the function is lo-

cally convex and a solution exists, the minimization

algorithms will be able to reach such solution, regard-

less of non-convexities of the function elsewhere.

In the particular domain of self - intersecting curve

ﬁtting to noisy point clouds there are very few refer-

ences on how to ﬁnd a reasonable initial guess for the

curve that is to be determined mathematical program-

ming.

References (Fl

ory and Hofer, 2010; Wang et al.,

2006) start with a user - deﬁned initial guess of the

curve sought. On the other hand, reference (Wang

et al., 2006) proposes to compute the quadtree parti-

tion of the point cloud and then extracts a sequence

ParametricCurveReconstructionfromPointCloudsusingMinimizationTechniques

of points which approximates the target shape. These

points are then used as initial control points of the ﬁt-

ting curve. However, the autors do not report the im-

plementation of such method.

Ref. (Zhao et al., 2011) mentions the usage of

a 2D grid of uniform cells (i.e., not a quadtree), on

which the cloud points fall. The curve, therefore,

must lie on the set of cells which receive sampled

points. The centers of these cells are calculated and

interpolated to obtain the initial curve. However, the

strategy to order these center points is not presented.

It must be noted that the ﬁtting of a PL or smooth

curve is precisely the problem of introducing a total

order among points which are representative of local

neighborhoods (either quadtree-based or cell-based)

of the point sample. The total order issue is partic-

ularly pressing for self-intersecting and non-Nyquist

curves.

2.4 Complexity Analysis

The complexity analysis allows to theoretically es-

timate the resources needed (time and memory) to

solve a problem using a given algorithm. It is cus-

tomary to express the performance of an algorithm

in terms of either (a) number of elementary opera-

tions, or (b) velocity of convergence. In case (a), an

operation is proposed as elementary for the solution

of the problem (e.g. comparison, assignment, query)

and then the number such operations required to solve

the problem for large problem sizes is computed in

the form of a function of n, the size of the problem

(O(n)). In case (b), a positive real number ζ is given,

meaning that the error in iteration k + 1 decreases

exponentially with respect to the error in iteration k

(ε

k+1

= (ε

)

), with 0.0 ≤ ε

< 1.0. Notice that using

(a) or (b) performance criteria avoids measuring the

execution time, which is inﬂuenced by the particular

hardware at hand. Instead, mathematical expressions

for (a) or (b), inherent to the problem, are used. De-

spite that, in general, the reviewed literature does not

address the topic of computational complexity of op-

timized parametric curve ﬁtting, we will discuss some

considerations of several authors at this respect.

Liu et al. in (Liu and Wang, 2008) argue that the

computation of the Hessian using direct second order

derivatives of the parametric curve is a very expen-

sive operation. Because of this, they classify different

approaches to calculate the point-to-curve distance,

based on the usage or avoidance of the second deriva-

tives of C (see section 2.2). This reference does not

calculate the complexity of the different approaches

used. The other literature reviewed ((Park and Lee,

2007), (Fl

ory, 2009), (Fl

ory and Hofer, 2010), (Song

et al., 2009), (Liu et al., 2005), (Wang et al., 2006))

reports the execution times but does not conduct a for-

mal complexity discussion.

It is the case that pre-processings (e.g. initial

guess ﬁndings) are usually assessed in terms of O(n)

while minimizations are assessed in terms of ε

con-

vergence. In order to correctly estimate the com-

putational expenses for optimized curve ﬁtting to

point clouds, we require the description of the com-

putational expenses for: (i) pre-processing (initial

guess generation) and (ii) optimization, on the same

grounds (either convergence speed of ε

or complex-

ity O(n)). Such an integration is not a trivial task.

2.5 Conclusions Literature Review and

Contribution of this Article

According to the taxonomy conducted in this litera-

ture review, there are several issues that remain open

in optimized curve ﬁtting to point clouds. These as-

pects include: (a) Finding of topologically correct ini-

tial guesses to offset the fact that possibly f and / or

the minimization region are non - convex. (b) Usage

of a function f which efﬁciently ﬁts the point set, al-

lowing for self - intersections and non-Nyquist sam-

ples. (c) Decimation of the number of control points

for C given that m control points imply a minimiza-

tion space of dimension R

. (d) Formal assessment

of the computational time and space required for the

solution (e.g. O(n) analysis).

In response to the previous considerations, this

article reports the implementation of: (i) An initial

PCA-based initial guess for P and therefore C, which

is topologically faithful to the point set, being able to

follow self - intersections and non-Nyquist samples.

(ii) Decimation of excessive control points by the im-

plementation of a curvature-based re-sampling, to re-

duce the dimension of the search space. (iii) A dis-

crete calculation of the distance point-curve by using

a re-sampling of the curve. (iv) A double penalization

included in the objective function, based on the dis-

tances cloud-point-to-curve and curve-to-cloud-point,

therefore avoiding the existence of spurious curls and

outliers in C.

It must be pointed out that, although a signiﬁcant

amount of work is required in the study of computa-

tional complexity, we do not intend to make a contri-

bution in such an aspect.

3 METHODOLOGY

The methodology used comprises the following

stages: (1) data pre-processing and (2) optimization

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

procedure. Stage (1) leads to a PL approximation of

the data to obtain a topologically correct initial guess

of the b-spline control polygon. Stage (2) implements

a Gauss-Newton optimization algorithm to minimize

the distance between the curve and the points S using

a penalized objective function. Fig. 3 summarizes the

procedure.

Preprocessing

Curvature-based

Resampling

PL Segments

Integration

PL Segments

Reconstruction

Gauss-Newton Algorithm

Jacobian

calculation

Objective Function

Evaluation

Stop criteria

met?

Curve noisy

point sample

Disconnected

PL Segments

Connected PL approximation

of the cloud points

Initial guess of

control polygon

Control Polygon

Update

New b-spline

approximation

Yes

Final b-spline

approximation

of the input data

Objective Function

Evaluation

Jacobian of

residuals

Figure 3: Block diagram of the proposed methodology.

3.1 Data Preprocessing

Given the S point set, an initial guess L for P (and

hence for C) is required, which is a rough PL approx-

imation of the curve C sought. This initial guess is

fundamental for the success of the optimization algo-

rithm that seeks C. L has correct topology, although

might not have a precise geometry. This initial guess

is calculated by a PCA pre-processing stage of our al-

gorithm.

Our approach is an extension of the work by (Ruiz

et al., 2011). The algorithm in (Ruiz et al., 2011) es-

timates the tangent to C at a particular point p of C

by running a PCA (i.e., generalized linear approxi-

mation Λ(λ) = p

+ λ. ˆv with starting point at p

direction ˆv and parameter λ) on the sample points of

such neighborhood. Those points are the subset of

S contained in a small circular ball B(r, p) based on

p. The goodness of the PCA can be evaluated using

a variation of the linear regression correlation coef-

ﬁcient ρ. In a ’normal’ (i.e., 1-manifold conditions)

curve neighborhood, the linear approximation is very

good, and therefore ρ ≈ 1.0. In self - intersecting (i.e.,

non-manifold) or non-Nyquist curve neighborhoods,

the linearity falls and ρ ≈ 0. At such neighborhoods,

the support region choosing the points to participate

in the PCA mutates from circular into an elliptical

one. This is a key feature of the algorithm because

it permits to deal with self-intersections. The pro-

cess continues with the adjacent neighborhoods until

a dead end is found (i.e., no more points are available

in the current direction of search), and another region

is explored. The procedure is repeated until S is com-

pletely traversed, delivering a set of disconnected PL

curves, S

{

...,c

}

, which approximates S.

In the present article, we improve (Ruiz et al.,

2011) by adding a novel integration strategy for the

s to obtain a single connected approximation of C

deﬁned as L. Let c

be PL curve fragments

to be merged, which happen to have their endpoints

close to each other (see Fig. 4(a)). In this case, the

distance criterium is obviously insufﬁcient to decide

which curve fragments should join. Therefore, an ad-

ditional criterium is used, namely the similarity of

tangent vectors at the curve endpoints. Based on it,

it is concluded that the pairs to join are (c

) and

) for the example shown in Fig. 4(b). In the gen-

eral case, however, the c

curve fragments integrate

unambiguously.

The PL curve, L, integrating the c

s is topologi-

cally equivalent to C

, meaning that L has self inter-

sections if C

does. However, L is not a good approxi-

mation of C

in the geometrical sense (i.e., it does not

lie in the ’center’ of the point set S). Therefore, L by

itself does not solve the problem.

The initial guess of the control polygon P for C

is obtained by re-sampling L, since one wants to use

the bare minimum necessary control points that re-

tain the topology of C. The re-sample of L is con-

trolled by the curvature: low curvature (large curva-

ture radius) regions can be represented by fewer con-

trol points, and vice versa. Given a point p

of L, the

local radius of curvature, R

may be approximated

by the radius of the circumference deﬁned by three

adjacent point samples, p

i−1

, p

i+1

. The curvature,

is given by K

. The larger the K

, the

tighter of the re-sample of L. The initial and ﬁnal

points of L are always included in the resulting re-

sampling. This curvature-based re-sampling strategy

ParametricCurveReconstructionfromPointCloudsusingMinimizationTechniques

R= δ

(a) Geometrically close endpoints.

(b) Similar end-tangents.

Figure 4: Criteria for integration of curve fragments c

strongly contributes to lower the computation time in

the subsequent optimized ﬁtting since less variables

need to be estimated (see Fig. 5).

We name as P the re-sampled version of L. Also

to keep notation simple, we use P to note the different

instances of itself (P

, P

, .., P

, ...), formed as its ver-

tices are relocated during the optimization iterations

k. Notice also that P is the control polygon for curve

3.2 Optimization Problem

The control polygon P resulting from the data pre-

processing in section 3.1 determines the topology of

C. The geometrical quality of P is, as expected, poor.

This means, the parametric curve controlled by poly-

gon P is not a principal curve for the point set S (i.e.,

does not cross the ’center’ of S). Therefore, the con-

trol points of P must now be used as decision vari-

ables to minimize the summation of the squared dis-

tances from the cloud points (i.e., points in S) to the

candidate curve C(u). A Gauss-Newton algorithm is

used to minimize the f function which expresses the

distances between the point cloud S and its approxi-

mating curve C.

The minimization problem is stated as follows:

GIVEN: A noisy point sample S = {p

, p

,..., p

} of

a planar parametric smooth (possibly self-intersecting

and with non-nyquist neighborhoods) curve C

GOAL: To determine the control polygon P that pro-

duces a b-spline curve C, minimizing

f =

∑

i=1

(6)



where r

is the residual or distance between cloud

point p

and the curve C. Informally, r

depends on

the distances from the cloud points in S to the curve

C and on the distances from the curve C to the point

clouds in C. As discussed later, these distances dif-

fer. Depending on the deﬁnition of r

, two different

strategies to minimize f arise, as discussed next.

parametric

curve

curl

outlier

leg

C(u

)

point

cloud S

(a) Distances Cloud Point to Curve.

outlier

leg

C(u

)

C(u

)

parametric

curve

(b) Distances Curve to Cloud Point.

Figure 6: Distances Cloud Points to/from Curve.

3.2.1 Strategy 1. Distance from Cloud Point to

Curve

We deﬁne the residuals as

= ||p

−C(u

)|| (7)

, where u

is the parameter in the domain of C which

deﬁnes the point C(u

) closest to p

. The term r

rep-

resents the distance measured from each cloud point

to the curve C (see Fig. 6(a)). This calculation of

the distance between a point and an algebraic curve is

a very expensive proposition because it implies the

calculation of common roots of a polynomial ideal

(see (Ruiz and Ferreira, 1996), (Kapur and Laksh-

man, 1992)). Notice that the vector p

−C(u

) is nor-

mal to the curve C at the point C(u

). To avoid the

computational expenses of algebraic root calculation,

we approximate C(u) in PL manner and calculate r

simply by an iterative process. We sample the do-

main for C(u), ([0,1]) getting U = [0,∆

,2∆

,...,1.0]

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

0 2 4 6 8 10

−2

−1

(a) Initial control polygon using L.

0 2 4 6 8 10

−2

−1

(b) Re-sampled version of L.

Figure 5: Curvature-based control point decimation to estimate the initial control polygon.

and approximate the current C curve with the poly-

line [C(0),C(∆

),C(2∆

),...,C(1.0)]. Calculating an

approximation of C(u

) for a given p

simply en-

tails to traverse [C(0),C(∆

),C(2∆

),...,C(1.0)] to

ﬁnd the C(N∆

) closest to p

. This is an O(n) process

(n=number of points), less elegant but much cheaper

than solving an algebraic system of equations (O(e

n=number of polynomials, (Kapur and Lakshman,

1992)), and sufﬁciently accurate.

Fig. 6(a) displays the distance from a particular

(emphasized) cloud point p

to its closest point C(u

)

on the current curve C. Such a distance has inﬂuence

in f as per Equation 6. Notice, however, that p

and

C(u

) (and hence f ) do not change if large legs and

curls appear in the synthesized C. Therefore, con-

sidering only the distance from cloud points to the

curve in Equation 6 permits the incorrect formation

of outlier legs and curls. The following section cor-

rects such a shortcoming.

3.2.2 Strategy 2. Inclusion of Distance from

Curve to Cloud Point

This section discusses how to include in the r

resid-

uals the distances from the curve points C

to the

cloud points p

(see Fig. 6(b)) to penalize in f the

growth of spurious outlier legs and / or curls just de-

scribed. If one can make spurious legs and curls to

inﬂate the objective function f , the minimization of

f avoids them. For any point p ∈ R

, the distance of

this point to S is a well deﬁned mathematical function:

d(p,S) = min

∈S

(||p − p

||). For the current discussion

the points p are of the type C(u

) (i.e., they are points

of curve C). The u

parameters to use are the sequence

U = [0, ∆

,2∆

,...,1.0], already mentioned.

Notice that d(p,S) = ||p

− p|| for some cloud

point p

∈ S. Let us deﬁne the point set A

(on the

curve C) as:

= {C(u) | u ∈ U ∧ d(C(u),S) = ||p

−C(u)||}

(8)

The set A

contains those points in the sequence

[C(0),C(∆

),C(2∆

),...,C(1.0)] that are closer to the

point p

∈ S than to any other point of S. We note with

the cardinality of A

. Observe that some Z

might

be zero, since p

could be far away from be curve C

and no point on the curve would have p

as its closest

in S. The set of all A

s could also be understood as a

partition of the curve C.

With the previous discussion, a new deﬁnition of

the residuals r

, to be used in Eq. 6, is possible:

= ||p

−C(u

)|| + (

) Σ

∈A

||C

− p

|| (9)

The ||p

− C(u

)|| in Eq. 9 considers the dis-

tance from cloud points in S to the curve C. The

term (

) Σ

∈A

||C

− p

|| expresses distances from the

curve C to the cloud points in S. This term penalizes

the length of the curve, by increasing f .

Figure 7: Clusters of Distances form Curve to Cloud Points.

Fig. 7 presents a simpliﬁed materialization of the

situation. The previous discussion applied to Fig. 7

implies the calculations shown in Table 1. Observe

that C

= C(u

), the point on C closest to p

is not the

exact one but the approximation mentioned in previ-

ous paragraphs (using a tight PL approximation of C).

3.2.3 Jacobian in the Gauss-Newton Method

The Gauss Newton method uses the Hessian approx-

imation H ≈ J ∗ J

, which works well in the cases in

which the function or region Ω are not convex. Be-

cause in our case f is not convex, we choose this

ParametricCurveReconstructionfromPointCloudsusingMinimizationTechniques

Table 1: Calculations using curve to cloud-point distances for example in Fig. 7.

C(u

) r

} 4 C

||p

−C

|| +

(||p

−C

|| + ||p

−C

+||p

−C

|| + ||p

−C

||)

} 3 C

||p

−C

|| +

(||p

−C

|| + ||p

−C

+||p

−C

||)

{} 0 C

||p

−C

} 2 C

||p

−C

|| +

(||p

−C

|| + ||p

−C

||)

} 2 C

||p

−C

|| +

(||p

−C

|| + ||p

−C

||)

} 2 C

||p

−C

|| +

(||p

−C

|| + ||p

−C

||)

} 3 C

||p

−C

|| +

(||p

−C

|| + ||p

−C

+||p

−C

||)

method for the minimization. The Gauss - Newton

method presents better convergence with small resid-

uals r

. Because of this reason, we use an good quality

initial guess (in this case, a PCA-based one), which

indeed produces low values in the residuals.

The Gauss-Newton optimization procedure em-

ploys an approximation to the Hessian matrix H. The

calculation of H implies several aspects: (i) it is ex-

pensive, (ii) it is actually a discrete approximation,

(iii) its usage in the search algorithm may mislead

it. Because of these reasons, for the present article

the Hessian matrix will be approximated as H ≈ J

where J is the Jacobian of the residuals with respect to

the decision variables. This approximation produces a

faster convergence of the decision variables to a local

minima than using the exact Hessian. The variables

to tune f are the x and y coordinates of the control

points (q

= (x

)) contained in the control polygon

P = [q

,...,q

]. The Jacobian of residuals is cal-

culated as follows:

J =







∂r

∂x

∂r

∂y

∂r

∂x

∂r

∂y

···

∂r

∂x

∂r

∂y

∂r

∂x

∂r

∂y

··· ··· ··· ··· ···

··· ··· ··· ··· ··· ··· ···

∂r

∂x

∂r

∂y

∂r

∂x

∂r

∂y

···

∂r

∂x

∂r

∂y







(10)

The dimension of the J matrix is (n × 2m) where

n = number of cloud points and m = number of points

in the control polygon. The calculation of each com-

ponent of the Jacobian is made numerically, using the

approximation of the partial derivative

∂r

∂x

∆r

∆x

. No-

tice that the variation of all decision variables are the

same ∆x.

The transformation of the control polygon is made

using the Jacobian of the residuals with the expression

k+1

= X

−





−1

r (11)

The dimensions associated with Eq. 11 are: X

(2m × 1), r (n × 1). X = [x

,...,x

]

just a convenient form for writing P. Notice that r =

,...,r

]

3.2.4 Criteria for Algorithm Termination

The Gauss-Newton procedure will continue ﬁnding

new control polygons until either of the following

conditions is met: (a) the variation of the objective

function from iteration k to k + 1 falls under a thresh-

old (| f

k+1

− f

| ≤ f

), (b) the values of the decision

variable do not signiﬁcantly change between iteration

k and k + 1 (|X

− X

k+1

| < δ

min

), (c) the iterations ex-

ecuted surpass a limit: (N

iter

> N

max

4 RESULTS AND DISCUSSION

4.1 Case Study 1. Simple Curves

4.1.1 Strategy 1. f based on Distance

Cloud-to-curve

The input data in this case of study corresponds to

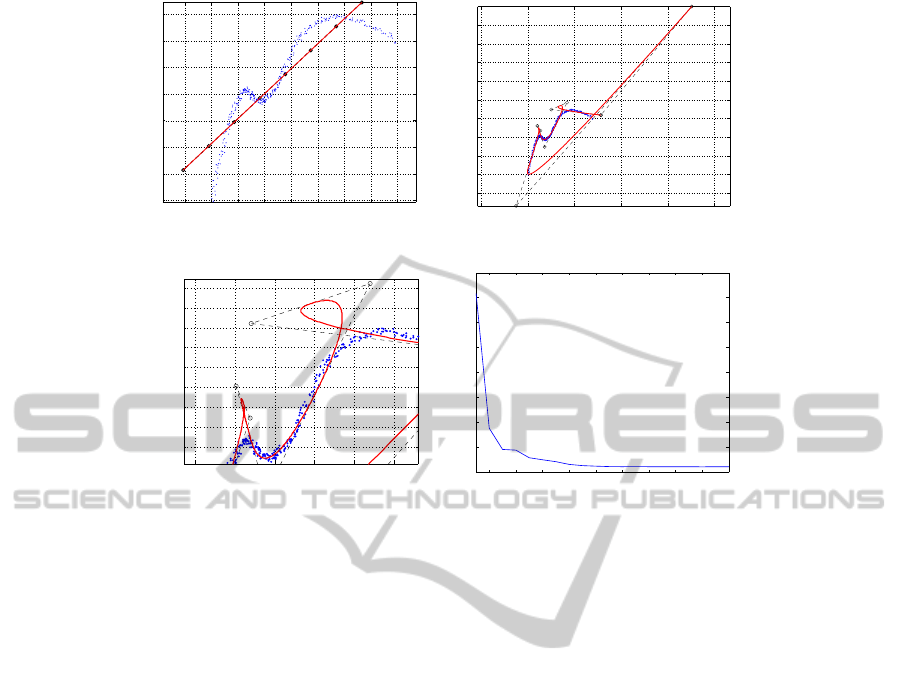
a simple curve, as per Fig. 8(a). The initial (naive)

guess for the control polygon P is a straight segment.

It is obtained from an overall linear regression using

all cloud points. A sequence of points is sampled on

such a straight segment which constitutes the initial

control polygon P. The rationale for this initial guess

is that the optimization process will, progressively, re-

locate the control points, until the parametric curve C

resulting from P, approximating C

is achieved. The

mathematical problem solved has the form discussed

in section 3.2.1.

Notice that the case currently discussed uses the

simple form of the f function, in which only distances

from S to C are considered (excluding distances from

C to S), as per Eq. 7. The results, in Fig. 8(b), show

that the b-spline curve tends to follow the shape of the

cloud points at some regions, but its endpoints are lo-

cated far away from their correct positions and some

curls appear. As discussed before in section 3.2.1 and

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

−1 0 1 2 3 4 5 6 7

(a) Point Cloud and Naive Initial P guess.

−5 0 5 10 15 20

−2

(b) Synthesized C with curls and Outlier Legs.

0 1 2 3 4 5

4.5

5.5

6.5

7.5

2 4 6 8 10 12 14 16 18 20

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

Iteration

(d) Objective Function f as function of iteration num-

ber.

Figure 8: Case Simple Curve C. Optimization uses naive initial guess and adds curve-to-cloud distance factor.

displayed in Fig. 6(a), such curls and otulier legs ap-

pear because the extent of C is not penalized in Eq.

4.1.2 Strategy 2. f Suplemented with Distance

Curve-to-cloud

With point set S as per Fig. 9(a), the minimized curve

ﬁtting is carried out now by adding curve-to-cloud

distances to the f objective function, as speciﬁed by

Eq. 9. This run uses the naive initial guess for P (i.e.,

sequence of colinear points). The resulting curve C is

correct, suppressing the curls and keeping the curve

attached to the ends of the input data. It is observed

that very few iterations are needed to yield satisfac-

tory results, showing fast convergence.

4.2 Case Study 2: Self-intersecting

Curve

The point set for this run series appears in Fig. 10(a).

As seen, it comes from a self - intersecting curve C.

The goal of this section is to evaluate the effects of a

smart initial guess for P, on the curve reconstruction

results. From now on, the form of the f function fo

minimize is the one in Eq. 9. This means, the dis-

tances cloud-to-curve and curve-to-cloud are used.

4.2.1 Naive Initial Guess for P

Fig. 10(a) shows the naive initial guess for the con-

trol polygon P (i.e., sequence of colinear points). No-

tice that a sufﬁcient number of points must be sam-

pled on the segment. Too few sampled points ob-

viously prevent following the topological evolutions

of the curve. Too many control points considerably

degrade the performance of the minimization algo-

rithm, since this number of points equals the dimen-

sion of the solution space. Fig. 10(b) shows that with

this naive guess, the reconstruction of C

dramatically

fails, even if a sufﬁcient number of control points are

provided on the straight segment of Fig. 10(a). Fig.

10(c) shows the evolution of f along the iterative pro-

cess.

4.2.2 PCA-based Initial Guess for P

The goal of this run is to test the effect of having a

topologically correct initial guess for P, the control

polygon of C. Fig. 11(a) shows the point set sam-

pled on a self-intersecting C. This ﬁgure also shows

an initial guess for the control polygon P found by the

PCA-based pre-processing. Observe that this initial P

captures the correct topology, although not the right

geometry, of C. Therefore, one requires a minimiza-

tion stage to relocate the vertices of P. The resulting

ParametricCurveReconstructionfromPointCloudsusingMinimizationTechniques

−1 0 1 2 3 4 5 6 7

(a) Point Cloud and Naive Initial P guess.

−1 0 1 2 3 4 5 6 7 8

(b) Final control polygon P and its ﬁt curve C.

2 4 6 8 10 12

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0.45

Iteration

ber.

Figure 9: Case Simple Curve C. Optimization uses naive initial guess and adds curve-to-cloud distance factor.

−2 0 2 4 6 8 10

−2

−1

(a) Point Cloud and Naive Initial P guess.

−2 0 2 4 6 8 10

−3

−2

−1

(b) Final control polygon P and its ﬁt curve C.

2 4 6 8 10 12

0.5

1.5

2.5

3.5

4.5

Iteration

number.

Figure 10: Open Curve with Self - intersection. C ﬁt without PCA pre-processing.

control polygon P and its corresponding curve C ap-

pear in Fig. 11(b). Fig. 11(c) shows the history if f

as the iterations take place.

4.3 Case Study 3: Sharp-cornered

Curve

Fig. 12(a) presents a point sample for a curve that has

only C

continuity. The Nyquist principle ((Shannon,

1949),(Nyquist, 1928)) applied to geometry sampling

requires that at this point the sampling distance raises

to inﬁnity and the sampling interval drops to zero,

implying that an inﬁnitely tight sample would be re-

quired to recover all the geometric information of the

original curve C

. The obvious compromise indicates

that, since only a ﬁnite sample is available, part of

the needle is amputated in the curve-reconstruction.

Unfortunately, even accepting such an amputation, is

very likely that in such cases (of non-Nyquist sam-

ples), the topology of the curve cannot be recovered.

The present example represents a very difﬁcult (non-

Nyquist) data set.

Fig. 12(a) presents the initial guess for the con-

trol polygon P originated using PCA. Fig. 12(b) dis-

plays the C the parametric curve ﬁnally achieved by

the minimization algorithm. Fig. 12(c) shows the his-

tory of the minimized f as function of the iteration.

As seen, since the application of PCA pre-processing

is able to correctly recover the topology of the curve

C, it is relatively straightforward for the minimization

process to tune up the vertices of P for the correct

placement of C. This efﬁciency is evident from the

fast convergence in very early iterations in Fig. 12(c).

4.4 Discussion

4.4.1 Initial Guess and Globality

The Hessian matrix for the problem in Eq. 6 is:

H =







∂

∂x

∂

∂x

∂y

∂

∂x

···

∂

∂x

∂y

∂

∂y

∂x

∂

∂y

∂

∂y

∂x

···

∂

∂y

··· ··· ··· ··· ·· ·

∂

∂y

∂x

∂

∂y

∂

∂y

∂x

···

∂

∂y







(12)

with the minimum search domain Ω being a subset

of R

. If the eigenvalues of H are all positive in Ω,

one would be in presence of an overall convex func-

tion f and the minimization algorithm would rapidly

ﬁnd the solution, guaranteed to be a global minimum.

Unfortunately, f as per Eq. 6 is not globally convex.

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

0 2 4 6 8 10

−2

−1

(a) Point cloud S and PCA-based initial control

polygon P

0 2 4 6 8 10

−2

−1

(b) Final control polygon P and its ﬁt curve C.

1 2 3 4 5 6 7 8 9 10

0.02

0.03

0.04

0.05

0.06

0.07

0.08

Iteration

number.

Figure 11: Open Curve with self-Intersections. C ﬁt using a PCA-based initial guess.

0 2 4 6 8 10 12

(a) Point cloud S and PCA-based initial control

polygon P.

0 2 4 6 8 10 12

(b) Final control polygon P and its ﬁt curve C.

2 4 6 8 10 12 14 16 18

0.03

0.04

0.05

0.06

0.07

0.08

0.09

0.1

0.11

0.12

Iteration

number.

Figure 12: Non-Nyquist point set. C ﬁt using a PCA-based initial guess.

local

minimum

global

minimum

PCA-based

initial

uess

naive initial

uess

Figure 13: Need of sensible guess with non-convex f .

Notice that H in Eq. 12 is not available and we use

H ≈ J

J instead. This replacement obviously does

not change the non-convexity of f .

Fig. 10 illustrates the effect of not having a glob-

ally convex function f . The initial guess for the poly-

gon P is not a sensible one, which means that the ini-

tial location in the Ω space is far from the minimum.

A poor initial guess for P produces a worng ﬁtting

result, as shown in Fig. 10(b). This wrong result ex-

plains our need of the PCA-based pre-processing. Fig

10(c) shows that the solution is a local minimum. f

is indeed minimized in a wrong neighborhood, and

the solution for P (and C) is equally wrong. Fig. 13

shows that, precisely because the non-convexity of f ,

an intelligent initial guess for P is required for the

minimization algorithm to ﬁnd a global minimum for

f . We claim here that the PCA-based pre-processing

improves the chances for an initial guess sufﬁciently

close to the global minimim and therefore partially

offsets the inherent difﬁculty represented by the non-

convexity of f .

4.4.2 Distance Curve to Point Cloud

As mentioned, the minimization using Eq. 7 per-

mits the formation of curls and leg outliers as per Fig.

8(b). This calculation of f includes only the distance

from the cloud points p

to the curve C. To prevent

these spurious formations we include in the f func-

tion the distance from the curve C to the point clouds

. The distance cloud-point-to-curve and curve-to-

cloud-point are not the same. Including the second

one (Eq. 9) makes f increase when outliers and curls

appear. This is a preventive rather than corrective

strategy, which ensures a correct topology and geom-

etry of the curve C.

4.4.3 Comparative Convergence

Fig. 14 displays, for a simple curve, a comparison

between convergence speeds achieved using only dis-

tance cloud-point-to-curve (Eq. 7) versus including

also distances curve-to-point-cloud (Eq. 9). The

two cases are called without and with penalization,

ParametricCurveReconstructionfromPointCloudsusingMinimizationTechniques

0 2 4 6 8 10 12 14 16 18 20

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0.45

Iteration

With penalization

Without penalization

(a) Double-distance Inﬂuence. Simple Curve.

0 2 4 6 8 10 12 14 16 18 20

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

Iteration

Relative delta f

With penalization

Without penalization

(b) Double-distance Inﬂuence. Simple Curve.

Convergence Speed.

Figure 14: Simple Curve Case. f as a function of iteration count. Inﬂuence of double-distance penalization.

0 2 4 6 8 10 12 14

0.5

1.5

2.5

3.5

4.5

Iteration

With PCA

Without PCA

(a) Initial Guess Inﬂuence. Self - intersecting

curve.

0 2 4 6 8 10 12 14

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

Iteration

Relative delta f

With PCA

Without PCA

(b) Initial Guess Inﬂuence. Self - intersecting

curve. Convergence speed.

Figure 15: Self - intersecting Curve case. f as a function of iteration count. Inﬂuence of PCA-based initial guess.

respectively. Fig. 14(a) shows that using the two

distances produces a faster reduction of the f fac-

tor. Fig. 14(b) indicates that the reduction in f

values more monotonous when penalization is used.

In other words, the optimization algorithm converges

faster to the solution. Notice that the convergence

when double-distance penalization is used (blue line),

the number of iterations required is 60% of the ones

required when only distance cloud-point-to-curve is

used (green line).

Fig. 15 illustrates, for a self - intersecting curve,

the comparison of convergence speeds by (1) using

PCA-based initial guess for the control polygon P and

by (2) abstaining from it. Fig. 15(a) indicates that, for

self - intersecting curves, the usage of a PCA-based

initial guess dramatically improves the convergence

speed of the optimization algorithm. Fig. 15(b) also

shows that the trend of the convergence is deﬁnitely

more monotonous when a PCA-based initial guess is

used. As in the discussion related to usage of double-

distance penalization of f , in this case (blue line) the

usage of PCA-based initial guess has an number of

iterations being 71% of the one required (green line)

when no sensible initial guess is used.

5 COMPLEXITY OF THE

ALGORITHM

Pre-processing. In Fig. 3, this stage refers to the

ﬁnding of an initial quess for P (and therefore C). A

sensible initial guess is found by (a) applying a PCA

algorithm to ﬁnd PL fragments c

, (b) joining the dis-

connected c

fragments into one (L), and (c) re - sam-

pling the L to obtain a PL approximation for P. If we

assume that the number of cloud points is n, the com-

plexity of the ellipse-based PCA is O(n

) ((Ruiz et al.,

2011)). This complexity is dominant and therefore in-

cludes the integration of PCA-based curve fragments

and the curvature-based re-sample of the initial guess

for P.

Optimization. In Fig. 3, this stage refers to the

minimization of the f function by tunning the deci-

sion variables (i.e., control points of P) so that C ﬁts

the point cloud S. This algorithm is controlled by a

while loop that stops when ε reaches a low value.

The calculation of the Jacobian, the update (which

implies a PL approximation) of the curve C and the

update of the function f together cost O(n

). There-

fore, the optimization stage costs O(g(ε) ∗ n

). Since

typically, g(ε) ∝ 1/(ε

), the complexity of the opti-

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

mization stage is O((n/ε)

According to the previous discussion, the over-

all complexity of the algorithm in Fig. 3 is O(n

(n/ε)

) = max(n

,(n/ε)

). Additional work is re-

quired to determine which one of n

and (n/ε)

dominant. A valid question to be posed is whether the

pre - processing might be removed, and its computa-

tional cost (O(n

)) spared. The answer is negative,

since a good quality initial guess for P is essential for

the optimization algorithm to converge to a topologi-

cally and geometrically valid solution. Fig. 10 illus-

trates the result for a run lacking a good quality initial

guess for P.

In the previous discussion, it must be pointed out

that the complexities considered are worst case ones.

Therefore, we present here a very conservative esti-

mation. For complexity estimation expected values

are also used.

6 CONCLUSIONS AND FUTURE

WORK

This article has presented the implementations of al-

gorithms to synthesize a parametric planar curve C as

an optimized ﬁt for a point cloud S sampled from an

unknown initial curve C

. The curve C is therefore an

approximation for C

The implemented method presents several nov-

elties with respect to the existing contributions by

other authors: (1) It is successful in recovering

self-intersecting and non-Nyquist curves. (2) It

implements a Principal Component Analysis pre-

processing which ﬁnds a topologically faithful PL ap-

proximation for P, the control polygon of C. (3) This

initial guess for P is optimized in the sense of using a

very reduced number of vertices, which are chosen

according to the local curvature of P. (4) The al-

gorithm avoids the expensive calculation of distance-

point-curve, which implies algebraic roots, by calcu-

lating a PL approximation of curve C in each iteration

and solving the distance-point-curve with this proxy

approximation. (5) The algorithm penalizes f by con-

sidering not only the distances of cloud points p

∈ S

to C but also the distances from curve points C

to S.

Since C is ﬁnite, theses distances are not equal. By

doing so, the implemented method avoids the genera-

tion of spurious curls and outlier legs. Finally, (6) the

implemented algorithms lower the computation time

required to solve the problem by introducing features

(2), (3), (4), above.

Ongoing work includes exploration of other mini-

mization algorithms (Quasi-Newton for large values

of residuals), usage of different objective functions

to obtain faster convergence, improvement in self-

tunning of the algorithms, usage of unequal weights

in the residuals of Eq. 9 and a more aggressive strat-

egy to minimize the number m of the control points of

P. Since the search space is R

, lowering m consid-

erably cuts the computing time for the minimization

of f .

REFERENCES

Blake, A. and Isard, M. (1998). Active contours: the ap-

plication of techniques from graphics, vision, control

theory and statistics to visual tracking of shapes in

motion. Springer.

ory, S. (2009). Fitting curves and surfaces to point clouds

in the presence of obstacles. Computer Aided Geo-

metric Design, 26(2):192–202.

ory, S. and Hofer, M. (2008). Constrained curve ﬁtting on

manifolds. Computer-Aided Design, 40(1):25–34.

ory, S. and Hofer, M. (2010). Surface ﬁtting and registra-

tion of point clouds using approximations of the un-

signed distance function. Computer Aided Geometric

Design, 27(1):60–77.

alvez, A., Iglesias, A., Cobo, A., Puig-Pey, J., and Es-

pinola, J. (2007). B

ezier curve and surface ﬁtting

of 3d point clouds through genetic algorithms, func-

tional networks and least-squares approximation. In

Proceedings of the 2007 international conference on

Computational science and Its applications-Volume

Part II, pages 680–693. Springer-Verlag.

Kapur, D. and Lakshman, Y. (1992). Elimination Methods:

An Introduction, pages 45–88. Academic Press.

Liu, Y. and Wang, W. (2008). A revisit to least squares

orthogonal distance ﬁtting of parametric curves and

surfaces. In Chen and Juttler, editors, Advances in

Geometric Modeling and Processing, volume 4975 of

Lecture Notes in Computer Science, pages 384–397.

Springer Berlin / Heidelberg.

Liu, Y., Yang, H., and Wang, W. (2005). Reconstructing b-

spline curves from point clouds–a tangential ﬂow ap-

proach using least squares minimization. In Proceed-

ings of the International Conference on Shape Mod-

eling and Applications 2005, pages 4–12. IEEE Com-

puter Society.

Nyquist, H. (1928). Certain topics in telegraph transmission

theory. Bell System Technical Journal.

Park, H. and Lee, J. (2007). B-spline curve ﬁtting based

on adaptive curve reﬁnement using dominant points.

Computer-Aided Design, 39(6):439–451.

Piegl, L. and Tiller, W. (1997). The NURBS book. Springer

Verlag.

Ruiz, O. E. and Ferreira, P. (1996). Algebraic Geometry

and Group Theory in Geometric Constraint Satisfac-

tion for Computer Aided Design and Assembly Plan-

ning. IIE Transactions. Focussed Issue on Design and

Manufacturing, 28(4):281–204. ISSN 0740-817X.

ParametricCurveReconstructionfromPointCloudsusingMinimizationTechniques

Ruiz, O. E., Vanegas, C. A., and Cadavid, C. (2011).

Ellipse-based principal component analysis for self-

intersecting curve reconstruction from noisy point

sets. The Visual Computer, 27(3):211–226.

Saux, E. and Daniel, M. (2003). An improved hoschek in-

trinsic parametrization. Computer Aided Geometric

Design, 20(8-9):513–521.

Shannon, C. (1949). Communication in presence of noise.

IRE, 37:10–21.

Song, X., Aigner, M., Chen, F., and J

uttler, B. (2009).

Circular spline ﬁtting using an evolution process.

Journal of computational and applied mathematics,

231(1):423–433.

Wang, W., Pottmann, H., and Liu, Y. (2006). Fitting

b-spline curves to point clouds by curvature-based

squared distance minimization. ACM Transactions on

Graphics (TOG), 25(2):214–238.

Zhao, X., Zhang, C., Yang, B., and Li, P. (2011). Adaptive

knot placement using a gmm-based continuous opti-

mization algorithm in b-spline curve approximation.

Computer-Aided Design.

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications