Hill Climbing versus Genetic Algorithm Optimization in Solving

the Examination Timetabling Problem

Siti Khatijah Nor Abdul Rahim

1,2

, Andrzej Bargiela

3,4

and Rong Qu

School of Computer Science, University of Nottingham (Malaysia Campus), Jalan Broga, 43500, Semenyih,

Selangor, Malaysia

Faculty of Computer and Mathematical Science, Universiti Teknologi MARA (Perak), 32610, Seri Iskandar,

Perak, Malaysia

School of Computer Science, University of Nottingham Jubilee Campus, Wollaton Road, Nottingham, NG8 1BB, U.K.

Institute of Informatics, Cracow Technical University, Kraków, Poland

Keywords: Slots Permutations, Hill Climbing (HC), Genetic Algorithm (GA).

Abstract: In this paper, we compare the incorporation of Hill Climbing (HC) and Genetic Algorithm (GA)

optimization in our proposed methodology in solving the examination scheduling problem. It is shown that

our greedy HC optimization outperforms the GA in all cases when tested on the benchmark datasets. In our

implementation, HC consumes more time to execute compared to GA which manages to improve the

quality of the initial schedules in a very fast and efficient time. Despite this, since the amount of time taken

by HC in producing improved schedules is considered reasonable and it never fails to produce better results,

it is suggested that we incorporate the Hill Climbing optimization rather than GA in our work.

1 INTRODUCTION

Timetabling can be defined as a process of creating

schedules that will list events and times at which

they are planned to occur. In many organizations or

institutions, timetabling is an important challenge

and considered a very tedious and time consuming

task. Normally, the personnel involve in preparing

the timetables will do it manually and in most cases

using a trial and error approach.

There are various areas of timetabling which

includes educational timetabling, sports timetabling,

transportation timetabling, nurse scheduling and etc.

Among the broad areas of these timetabling

problems, educational timetabling is one of the most

studied and researched area in the timetabling

literature. This is due to the requirement of preparing

the timetables periodically (quartely, annually and

etc).

Educational timetabling includes school

timetabling (course-teacher timetabling), university

course timetabling, university examination

timetabling and etc. In this work, our focus is the

university examination timetabling problem. For this

timetabling problem, in most universities nowadays,

the students are given the flexibility to enroll for

courses across faculties. This makes this kind of

timetabling problem more challenging to solve.

Numerous approaches or methods have been

proposed since the year 1960s which have attracted

reseachers form the Operational Research and

Artificial Intelligence area (Qu et al., 2009). To date,

the number of approaches or methods proposed to

solve the examination timetabling problems is

increasing. The example of the methods proposed

are graph based sequential techniques, constraint

based techniques, local search based techniques,

population based algorithms, hyper heuristics,

hybridisations and etc. (Gueret et al., 1995); (Taufiq

et al., 2004); (Dowsland and Thompson, 2005);

(Asmuni et al., 2009); (Burke et al., 2010c) and etc.

The strong inter-dependencies between exams

due to the many-to-many relationship between

students and exams has made the examination

timetabling a very challenging computational

problem. The general objective of the examination

timetabling is to generate schedule which is feasible

by making sure all exams are scheduled and that all

students can sit for the exams that they enrolled on

without any problems. Two types of constraints

defined in the timetabling literatures are:

a) Hard Constraints

241

Rahim S., Bargiela A. and Qu R..

Hill Climbing versus Genetic Algorithm Optimization in Solving the Examination Timetabling Problem.

DOI: 10.5220/0004286600430052

In Proceedings of the 2nd International Conference on Operations Research and Enterprise Systems (ICORES-2013), pages 43-52

ISBN: 978-989-8565-40-2

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

These constraints must be fulfilled at all times. The

basic hard constraint is that the exams with a

common student cannot be scheduled in the same

period. Another important hard constraint that needs

to be obeyed is the room capacity; i.e. there must be

enough space in a room to accommodate all students

taking a given exam. A timetable which fulfils all

the hard constraints is called a feasible timetable.

b) Soft Constraints

Soft Constraints are not very crucial but their

satisfaction is advantageous to students and/or the

institution. An example of a soft constraint is to

space out exams taken by individual students so that

they have adequate revision time between their

exams. Normally it is impossible to satisfy all soft

constraints therefore there is a need for a

performance function measuring the degree of

fulfilment of these constraints.

Our approach in producing feasible timetables

starts by performing datasets retrieval, pre-

processing of student-exam data, followed by

allocating exams to time-slots and next performing

optimization process to improve the quality of the

schedules. Greater explanations will be given in the

next section.

1.1 Overview of the Proposed Method

The steps of our proposed work in creating feasible

and quality examination schedules are datasets

retrieval, pre-processing, scheduling and lastly

timetable optimization as illustrated in Figure1.

Figure 1: The Work Flow in This Research.

Datasets retrieval can be defined as a task to

populate the four sets in the timetabling problem as

defined by (Burke et al., 2004). The 4 sets are the

times (T), resources (R), meetings (M) and

constraints (C). The task involves the process of

retrieving the datasets that are freely made available

to the public over the internet. In this research, we

have retrieved benchmark datasets that are widely

tested by many researchers from the University of

Nottingham and University of Toronto. These

benchmark datasets contain information or files

pertaining to students, exams, enrollments and other

data and constraints.

In the next step, which is the pre-processing

stage, a more meaningful information and higher

level data will be generated. This stage will be

underpinned by the methodology of Granular

Computing of generating semantically meaningful

information granules and their experimental

validation (Bargiela and Pedrycz, 2008). The

aggregated data will supply us with the important

information that is needed in order to create

timetables that are feasible which satisfy the basic

constraints. One example of the information

obtained from the pre-processing is the identification

of the clashing exams. By identifying this

information, later during the scheduling, we will be

able to schedule timetables that will fulfill the hard

constraint; for instance there should not be one

student having two exams simultaneously. In other

conventional approaches, this is not the case.

Without the pre-processing stage, the clashing

information is implicit in data, thus a lot of

permutations requiring a lot of time need to be done

in order to create a feasible timetable. This problem

can be avoided in our approach. Hence our approach

deals only with feasible solutions. The pre-

processing is explained in detail in (Rahim et al.,

2009).

Scheduling will be done next by using the

derived information from the previous process. The

scheduling is done by allocating exams with the

highest conflicts first to the available timeslots and

followed by exams with lower conflicts. Splitting

and merging of timeslots were done for exams in a

slot that can be reassigned to other slots consisting

non-conflicting exams. The allocation process has

been elaborated in detail in (Rahim et al., 2012). The

timetable generated at this stage is based on the pre-

processed data therefore it will always fulfill the

hard constraints.

The arrangements of the exams in the schedule

generated earlier might not fulfill many of the soft

constraints. Therefore, in order to improve the

quality of the exam schedules generated, we have

employed an optimization process. The optimization

consists of three procedures: i) Minimization of

Total Slot Conflicts, ii) Permutations of exams slots

and iii) Reassignments of exams between slots.

(Rahim et al., 2012). Please note that all the

ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems

242

optimization procedures mentioned here are done in

sequence but they are independent of each other.

In this paper, we will not be discussing about

these procedures in detail (it can be found in (Rahim

et al., 2012)), but will be looking at the possibility of

improving the quality of the schedules by

substituting the second step of optimization: the

permutations of exams slots which is a local search

procedure with a more effective procedure.

Realizing that our existing method (permutations

of exams slots), is a local search procedure, we

would like to incorporate a global search procedure

in order to see whether it could generate better

quality schedules. For this purpose, we have

implemented Genetic Algorithm (GA) to substitute

the permutations of exams slots in the optimization

process.

Genetic algorithm has been chosen as an

alternative approach to our implementation because

it has been proven a good way of producing good

examination timetables (Burke et al., 1994a); (Burke

et al., 1994b); (Gyori et al., 2001); (Ulker et al.,

2007). Besides, it has been mentioned that the

hybridisations of GA with some local search have

led to some success in this area. (Qu et al., 2009).

Figure 2: Scheduling and Optimization Steps Before and

After GA Substitution.

Above we presented the diagram (Figure 2) to

illustrate a summary of the work done in our

research (Rahim et al., 2012) which shows the

sequence of every process involve and the part that

will be substituted by GA. Please note that the whole

set of optimizations is done twice, therefore first and

second order optimization can be seen in the

diagram.

2 OPTIMIZATION METHODS

Normally, the cost of the initial timetables generated

by the allocation method mentioned earlier is a bit

high. This is because the ordering of exams to slots

might not satisfy many of soft constraints. An

example is the gap between conflicting exams is not

spaced out equally. The cost of the schedules is

measured by objective function proposed by Carter

(Carter et al., 1996) as below:





pi| - pj|

(1)

where N is the number of exams, sij is the

number of students enrolled in both exam i and j, pj

is the time slot where exam j is scheduled, pi is the

time slot where exam i is scheduled and T is the total

number of students. According to this cost function,

a student taking two exams that are | pj - pi | slots

apart, where | pj - pi | ={1, 2, 3, 4, 5 }, leads to a cost

of 16, 8, 4, 2, and 1, respectively.

The lower the cost obtained, the better is the

quality of the schedule, since the gap between two

consecutive exams allows students to have

additional revision time.

2.1 Hill Climbing Optimization

In this optimization process, the permutations of

exam slots in the spread matrix (Rahim et al., 2009),

(Rahim et al., 2012) are done. This process involves

shuffling of slots or columns and so as block shifting

and swapping. The procedure started by reading a

spread matrix which is a matrix indicating how

many students taking an exam from slot ‘i’ and ‘j’.

The permutations in the spread matrix involved

swapping of slots and repetitions of block shifts.

Each slot will be swapped with another slot. This is

done by doing provisional swapping and the Carter

cost will be evaluated first. If the cost is reduced, the

swap will be remembered and the exam proximity

matrix will be updated according to this swap. Due

to this, we call this kind of optimization as a greedy

Hill Climbing (HC). The term greedy here refers to

the fact that we always take the best value whenever

HillClimbingversusGeneticAlgorithmOptimizationinSolvingtheExaminationTimetablingProblem

243

we found one. A number of repetitions of block shift

and swapping are done in order to ensure the search

space is explored in different directions so that

global optimum of the solutions can be found.

2.2 Genetic Algorithm Optimization

Genetic algorithm is a search heuristic that mimics

the process of natural evolution. It simulates the

inheritance of living beings and it is a widely used

method to solve optimization and search problems.

Genetic algorithm is a procedure used to find

approximate solutions to search problems by

mimicking the evolutionary biological process. It

operates on a population of solutions represented by

some encoding. Each member or unit of the

population consists of a number of genes,

representing a unit of information. This procedure

begins by creating an initial population (normally

randomly generated). Next the solution members are

evaluated by computing their fitness (or quality).

The selection procedure than reproduce more copies

of individuals with higher fitness values. The

selection procedure influences the search direction

towards promising areas. Genetic operators such as

crossover (mating two parents) and mutation (slight

random changes) are used to create new populations.

The important parameters include the population

size, crossover rate and mutation rate.

In our Genetic Algorithm implementation, we

defined the original parent as P0, which is a data

structure with the initial ordering of slots (1 …. N)

where N is the number of slots. GA creates a new

parent by moving position of the rows in blocks to

the new position, then appends it to array P. A

member of <npar> parents will be generated.

Generation of the new parents is just by shifting the

rows which in the end is the new representation of

the original parent with a magnitude maximum

distance of npar – 1. Therefore, if it is just a window

shift, there will be identical parents.

We then generated the new offspring. The

number of offspring to be generated is equals to npar

x npar -1. Each of the parents will be crossed over

with all other parents at a certain point R. The result

will be added to “o” which is the overall population.

The best parent will be automatically selected to

become one of the next generation parent. Then the

next best parent with the lowest cost will be

selected. The parent will be included in the next

population and the process continues for certain

number of generations.

3 COMPUTATIONAL RESULTS

AND DISCUSSION

The experiment in this work was performed on all

13 datasets in the Toronto benchmark repository

[ftp://ftp.mie.utoronto.ca/pub/carter/testprob] and

also on the Nottingham dataset

[http://www.cs.nott.ac.uk/~rxq/files/Nott.zip]. For

the sake of comparability with other studies in the

literature, these problems are considered here as an

uncapacitated scheduling problem. Uncapacitated

means the total room capacity in each time slot is

not considered.

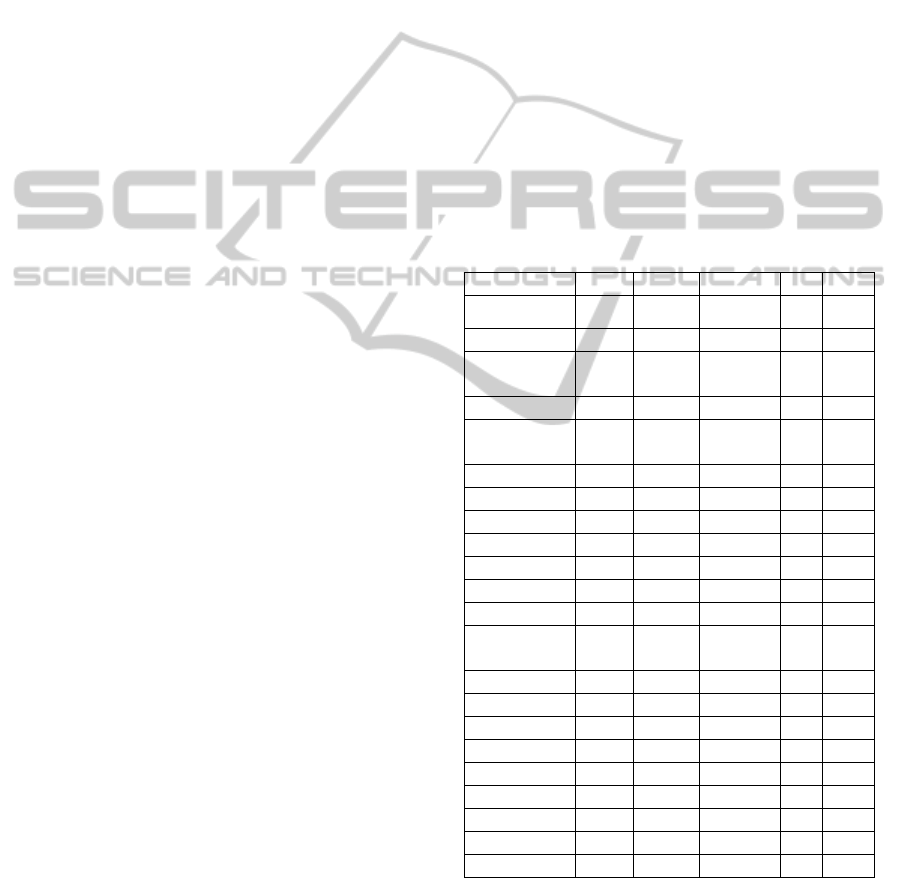
The characteristics of all the datasets are listed in

Table 1. For the Toronto datasets, based on the

survey made by (Qu et al., 2009), 8 out of 13

problem instances exist in 2 versions. We will use

version I of the datasets which are extensively tested

by other researchers.

Table 1: The characteristics of the Datasets.

(a) (b) (c) (d) (e) (f)

nott (a/b) 800 7896 33997 23 0.03

car-s-91 (I) 682 16925 56877 35 0.13

car-s-91 (II) 682 16925 56242/

56877

35 0.13

car-f-92 (I) 543 18419 55522 32 0.14

car-f-92 (II) 543 18419 55189/

55522

32 0.14

ear-f-83(I) 190 1125 8109 24 0.27

ear-f-83(II) 189 1108 8014 24 0.27

hec-s-92(I) 81 2823 10632 18 0.42

hec-s-92(II) 80 2823 10625 18 0.42

kfu-s-93 461 5349 25113 20 0.06

lse-f-91 381 2726 10918 18 0.06

pur-s-93 (I) 2419 30029 120681 42 0.03

pur-s-93 (II) 2419 30029 120686/

120681

42 0.03

rye-f-92 486 11483 45051 23 0.07

sta-f-83(I) 139 611 5751 13 0.14

sta-f-83(II) 138 549 5689 35 0.14

tre-s-92 261 4360 14901 23 0.18

uta-s-92(I) 622 21266 58979 35 0.13

uta-s-92(II) 638 21329 59144 35 0.13

ute-s-92 184 2749 11793 10 0.08

yor-f-83 (I) 181 941 6034 21 0.29

yor-f-83 (II) 180 919 6012 21 0.29

(a)Name of Dataset; (b) No of Exams; (c) No of Students;

(d) No of Enrollments; (e) Required No of Slots; (f)

Conflict Density.

We have shown the results obtained by using

Hill Climbing and Genetic Algorithm optimization

ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems

244

on the initial feasible schedule generated by our

allocation method before performing other

optimization process (Rahim et al., 2012) in Table 2

to Table 15. For the Hill Climbing, we recorded the

worse and the best cost during the process

(permutations of slots), and for the Genetic

Algorithm, we presented the cost produced after

Generation 1 (Gen 1) and Generation 15 (Gen 15).

The best cost produced for each type of

optimization is accepted and the ordering of slots

were rearranged accordingly before doing further

optimization : reassignment of exams between slots

(Rahim et al., 2012) and later repeating the whole set

of the optimization process until there is no

improvement in the schedule cost (Rahim et al.,

2012). The accepted cost together with the CPU time

taken for each process can be seen in these tables.

Table 2: Results obtained by optimization for nott.

Dataset

Initial

Cost

Accepted

Cost

CPU Time

(seconds)



Hill Climbing

Worse

cost

Best

cost

nott

31.95 10.94

10.94 187.27

38.99

Genetic Algorithm



Gen 1 Gen 15



28.03 14.74 14.74 3.39

Table 3: Results obtained by optimization for car-f-92(I).

Dataset

Initial

Cost

Accepted

Cost

CPU Time

(seconds)



Hill Climbing

Worse

cost

Best

cost

car-f-92

(I)

8.89 5.36

5.36 268.97

9.43

Genetic Algorithm



Gen 1 Gen 15



8.07 6.68 6.68 5.11

Table 4: Results obtained by optimization for car-s-91(I).

Dataset

Initial

Cost

Accepted

Cost

CPU Time

(seconds)



Hill Climbing

Worse

cost

Best

cost

car-s-91

(I) 10.43 6.26

6.26 351.39

11.77

Genetic Algorithm



Gen 1 Gen 15



9.37 8.10 8.10 5.99

Table 5: Results obtained by optimization for ear-f-83(I).

Dataset

Initial

Cost

Accepted

Cost

CPU Time

(seconds)



Hill Climbing

Worse

cost

Best

cost

ear-f-83

(I)

62.57 40.45 40.45 136.77

72.69

Genetic Algorithm



Gen 1 Gen 15



53.51 48.99 48.99 1.78

Table 6: Results obtained by optimization for hec-s-92(I).

Dataset

Initial

Cost

Accepted

Cost

CPU Time

(seconds)



Hill Climbing

Worse

cost

Best

cost

hec-s-92

(I)

22.55 12.52

12.52 27.52

22.83

Genetic Algorithm



Gen 1 Gen 15



19.39 14.14 14.14 2.30

HillClimbingversusGeneticAlgorithmOptimizationinSolvingtheExaminationTimetablingProblem

245

Table 7: Results obtained by optimization for kfu-s-93.

Dataset

Initial

Cost

Accepted

Cost

CPU Time

(seconds)



Hill Climbing

Worse

cost

Best

cost

kfu-s-93 29.89 16.06 16.06 40.36

37.79

Genetic Algorithm



Gen 1 Gen 15



26.81 20.06 20.06 2.48

Table 8: Results obtained by optimization for lse-f-91.

Dataset

Initial

Cost

Accepted

Cost

CPU Time

(seconds)



Hill Climbing

Worse

cost

Best

cost

lse-f-91 22.42 14.63 14.63 26.59

23.77

Genetic Algorithm



Gen 1 Gen 15



19.40 17.20 17.20 2.25

Table 9: Results obtained by optimization pur-s-93(I).

Dataset

Initial

Cost

Accepted

Cost

CPU Time

(seconds)



Hill Climbing

Worse

cost

Best

cost

pur-s-93

(I)

14.27 6.69 6.69 321.05

14.91

Genetic Algorithm



Gen 1 Gen 15



11.94 8.47 8.47 7.97

Table 10: Results obtained by optimization for rye-f-92.

Dataset

Initial

Cost

Accepted

Cost

CPU Time

(seconds)



Hill Climbing

Worse

cost

Best

cost

rye-f-92 28.55 12.68 12.68 73.17

31.50

Genetic Algorithm



Gen 1 Gen 15



19.04 16.46 16.46 3.25

Table 11: Results obtained by optimization sta-f-83(I).

Dataset

Initial

Cost

Accepted

Cost

CPU Time

(seconds)



Hill Climbing

Worse

cost

Best

cost

sta-f-83 193.47 158.43 158.43 10.28

201.95

Genetic Algorithm



Gen 1 Gen 15



172.80 163.12 163.12 0.52

Table 12: Results obtained by optimization for tre-s-92.

Dataset

Initial

Cost

Accepted

Cost

CPU Time

(seconds)



Hill Climbing

Worse

cost

Best

cost

tre-s-92

13.25 9.84 9.84 66.34

14.81

Genetic Algorithm



Gen 1 Gen 15



12.76 11.70 11.70 3.17

ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems

246

Table 13: Results obtained by optimization utas-s-92(I).

Dataset

Initial

Cost

Accepted

Cost

CPU Time

(seconds)



Hill Climbing

Worse

cost

Best

cost

uta-s-92

(I)

6.59 4.23

4.23 455.94

7.30

Genetic Algorithm



Gen 1 Gen 15



6.19 5.22 5.22 6.54

Table 14: Results obtained by optimization for ute-s-92.

Dataset

Initial

Cost

Accepted

Cost

CPU Time

(seconds)



Hill Climbing

Worse

cost

Best

cost

ute-s-92 43.25 31.79 31.79 2.91

56.97

Genetic Algorithm



Gen 1 Gen 15



35.77 32.96 32.96 1.30

Table 15: Results obtained by optimization for yor-f-83(I).

Dataset

Initial

Cost

Accepted

Cost

CPU Time

(seconds)



Hill Climbing

Worse

cost

Best

cost

yor-f-83

(I)

56.31 43.36

43.36 46.99

59.04

Genetic Algorithm



Gen 1 Gen 15



50.77 47.50 47.50 0.75

Based on the results presented in Table 2 to

Table 15, it can be seen clearly that our proposed

greedy Hill Climbing (HC) method has

outperformed GA in all cases during the

optimization when tested on the benchmark datasets.

All the results produced by GA for all the datasets

after generation 15 (Gen 15) were not able to

outperform results produced by HC.

It is worth highlighting here that the cost

obtained by GA for all datasets at generation 1 (Gen

1) are quite encouraging, where they are much lower

than the worse cost obtained by HC. However, all of

them failed to outperform the cost obtained by HC

after generation 15 (Gen 15).

Using the data gathered from the experiments on

all the datasets, we have plotted graphs for the cost

(1) versus the Total Slot Conflicts as in Figure 3 and

Figure 4. Figure 3 and 4 show the graphs for the

cost(1) versus the Total Slot Conflicts plotted for all

benchmark datasets tested. Diagram (a1), (b1), (c1),

(d1), ….. (n1) are the graphs (line-graphs) when HC

optimization used where as diagram (a2), (b2), (c2),

(d2),…… (n2) are the graphs (dotted-graphs) plotted

when GA optimization used. The diagrams in these

figures are arranged according to the sequence of

datasets from Table 2 to Table 15.

Based on the graphs presented, the horizontal

line constructed from the second data point to third

data point in diagram (a1) to (n1) is due to reduction

of cost via permutations of exams slots (greedy HC)

which did not involve any augmentation of total

slots conflicts (Rahim et al., 2012). The dotted line

from the first data point to the second data point in

each diagram (a2) to (n2) is constructed based on the

GA optimization discussed earlier in this paper.

The dotted lines in this stage showed that a

significant reduction in terms of the initial cost has

been achieved by performing the GA optimization.

These lines also showed that our GA implementation

managed to substitute the HC implementation and

was incorporated successfully in the whole set of our

optimization process. (Rahim et al., 2012).

One of the obvious thing that can be seen in the

graphs is that the line constructed by GA

optimization is not always horizontal. This is

because, the crossover and mutation of exam slots in

the GA optimization process had changed the

assignments of some exams to slots to ensure the

feasibility of the schedules, thus changing the

existing number of total slots conflicts. This is not

the case duirng HC optimization where by the total

exam-slot conflict does not change because the

individual exams to slots remain as before

permutations. (Rahim et al., 2012).

An interesting point to note is the computational

time taken to execute both methods. Even though

GA did not surpass HC in all cases, however the

time taken to execute the process was incredibly fast

compared to our HC implementation. We have

managed to implement a simple, straightforward and

quite effective GA which consumed very little

HillClimbingversusGeneticAlgorithmOptimizationinSolvingtheExaminationTimetablingProblem

247

5 10 15 20 25 30 35 40

8.2

8.4

8.6

8.8

9.2

9.4

9.6

9.8

Tot al s lot conf lict * 1000

Carter cost

(a1)

5 10 15 20 25 30 35 40

7.5

8.5

9.5

10.5

Carter cost

Total slot conflic t * 1000

(a2)

4 5 6 7 8 9 10

12.2

12.4

12.6

12.8

13.2

13.4

13.6

13.8

Carter c ost

Total slot conflic t * 1000

(b1)

5 5.5 6 6.5 7 7.5 8 8.5 9 9.5

12.2

12.4

12.6

12.8

13.2

13.4

13.6

13.8

Carter cost

Total sl ot confl ict * 1000

(b2)

5 6 7 8 9 10 11 12

16.5

17.5

18.5

Carter cost

Total slot c onflict * 1000

(c1)

6 7 8 9 10 11 12

16.5

17.5

18.5

19.5

Carter cost

Tota l s lot conf li ct * 1000

(c2)

35 40 45 50 55 60 65 70 75

3.54

3.56

3.58

3.6

3.62

3.64

3.66

3.68

3.7

3.72

3.74

Carter cost

Total s lot confl ict * 1000

(d1)

45 50 55 60 65 70 75

3.55

3.6

3.65

3.7

3.75

3.8

Carter cost

Total slot c onflict * 1000

(d2)

10 12 14 16 18 20 22 24

1.26

1.26 1

1.26 2

1.26 3

1.26 4

1.26 5

1.26 6

1.26 7

Carter cost

Total slot c onflict * 1000

(e1)

12 14 16 18 20 22 24

1.24

1.245

1.25

1.255

1.26

1.265

1.27

1.275

Carter cost

Total sl ot confl ict * 1000

(e2)

10 15 20 25 30 35 40

4.5

4.6

4.7

4.8

4.9

5.1

5.2

5.3

Carter cost

Total slot c onflict * 1000

(f1)

15 20 25 30 35 40

4.6

4.7

4.8

4.9

5.1

5.2

5.3

5.4

Carter cost

Total sl ot confl ict * 1000

(f2)

10 12 14 16 18 20 22 24

3.7

3.75

3.8

3.85

3.9

3.95

4.05

4.1

4.15

4.2

Carter cost

Total slot c onflict * 1000

(g1)

15 16 17 18 19 20 21 22 23 24

3.65

3.7

3.75

3.8

3.85

3.9

3.95

4.05

4.1

4.15

Carter cost

Total s lot confl ict * 1000

(g2)

Figure 3: Cost (1) vs. the Total Slot Conflicts for

Benchmark Datasets (Using Hill Climbing (a1)-(g1) vs

Genetic Algorithm (a2)-(g2)).

4 6 8 10 12 14 16

Carter cost

Total slot c onflict * 1000

(h1)

5 6 7 8 9 10 11 12 13 14 15

Carter cost

Total s lot confl ict * 1000

(h2)

5 10 15 20 25 30 35

7.1

7.2

7.3

7.4

7.5

7.6

7.7

7.8

Carter cost

Total slot c onflict * 1000

(i1)

10 15 20 25 30 35

6.7

6.8

6.9

7.1

7.2

7.3

7.4

7.5

7.6

7.7

Total s lot c onflic t * 1000

Carter cost

(i2)

155 160 16 5 170 175 180 185 190 195 200 205

1.5045

1.50 5

1.5055

1.50 6

1.5065

1.50 7

Carter cost

Total slot c onflict * 1000

(j1)

160 165 170 175 180 185 190 195 200 205

1.5

1.505

1.51

1.515

1.52

1.525

1.53

1.535

Carter cost

Total slot confli ct * 1000

(j2)

8 9 10 11 12 13 14 15

4.25

4.3

4.35

4.4

4.45

4.5

4.55

4.6

4.65

4.7

4.75

Carter cost

Total slot c onflict * 1000

(k1)

9 10 11 12 13 14 15

4.35

4.4

4.45

4.5

4.55

4.6

4.65

4.7

4.75

4.8

Carter cost

Total slot c onflict * 1000

(k2)

3.5 4 4.5 5 5. 5 6 6.5 7 7. 5

14.8

15.2

15.4

15.6

15.8

16.2

16.4

16.6

16.8

Carter cost

Total slot c onflict * 1000

(l1)

4 4.5 5 5. 5 6 6.5 7 7. 5

15.2

15.4

15.6

15.8

16.2

16.4

16.6

16.8

Carter cost

Total s lot confl ict * 1000

(l2)

25 30 35 40 45 50 55 60

1.14

1.16

1.18

1.2

1.22

1.24

1.26

Carter cost

Total s lot confl ict * 1000

(m1)

25 30 35 40 45 50 55 60

1.14

1.16

1.18

1.2

1.22

1.24

1.26

1.28

1.3

Carter cost

Total sl ot confl ict * 1000

(m2)

40 42 44 46 48 50 52 54 56 58 60

3.25

3.3

3.35

3.4

Carter cost

Total slot c onflict * 1000

(n1)

42 44 46 48 50 52 54 56 58 60

3.24

3.26

3.28

3.3

3.32

3.34

3.36

3.38

3.4

3.42

3.44

Carter cost

Total s lot confl ict * 1000

(n2)

Figure 4: Cost (1) vs. the Total Slot Conflicts for

Benchmark Datasets (Using Hill Climbing (h1)-(n1) vs

Genetic Algorithm (h2)-(n2)).

ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems

248

amount of time to improve the initial feasible

schedule, although majority researchers claimed that

the GA took a very huge time in order to solve the

scheduling problem (for example claimed by

(Abramson, 1992)).

This advantage (minimal time requirement)

could offer even more advantage, because based on

the results presented earlier we can predict that

addition to the number of iterations or generations

(with the aim to generate better offsprings) to the

GA execution will add only little more

computational time that would definitely be very

acceptable.

However, unfortunately this is not the case. The

increase in the number of generations has not given

any benefit to the reduction of the cost of the exam

schedule generated. We have experimented 15

generations, but it seems like the highest number of

generations that manage to reduce the cost is

generation 12 (car-f-92(I)). Recall that we have

mentioned previously, a second round of

optimization was done in order to test whether it

could reduce the cost further. Therefore, after

performing reassignment of exams on the schedules

obtained by the GA optimization (Rahim et al.,

2012), we have repeated the GA optimization one

more time. As can be seen in Table 16, the highest

number of generations that could reduce the

schedule cost is generation 11 (rye-f-92) even

though 15 generations was tested.

The second round has improved the cost(1) for

most of the datasets (exceptional for nott, carf92,

kfus93, purs93, and utes9) and this is illustrated in

diagram (a2) until (n2) by the third data point to the

fourth data point.

The final results obtained by HC and GA

methods which later were further improved by

reassignments of exams (Rahim et al., 2012) were

compared and can be found in Table 17. It can be

seen clearly that HC outperforms GA in all cases,

though the execution time recorded was a bit high in

comparison to GA, but the amount of time taken was

still reasonable which is only a few hundreds

seconds CPU time.

4 CONCLUSIONS

In conclusion, it is shown that GA has been proven

to be a good method to reduce the cost of the initial

feasible timetable. With a robust implementation, it

managed to explore the search space efficiently and

produce good quality timetable with an incredibly

fast execution time.

Table 16: Number of Generations That Could Improve the

Schedule Cost During GA Optimization.

Dataset

First Order

Optimization:

Cost Improved

Until Iteration

Second Order

Optimization:

Cost Improved

Until Iteration

notts 7 0

carf92 12 0

cars91 9 2

earf83 7 6

hecs92 6 7

kfus93 10 0

lsef91 8 4

purs93 11 0

ryef92 8 11

staf83 6 4

tres92 8 5

utas92 10 4

utes92 3 0

yorf83 6 3

Table 17: Final Cost Produced Using HC versus GA

Optimization.

Dataset

Final Cost

Produced after All

Optimizations

Processes For HC

(Rahim et al.,

2012)

Final Cost

Produced after All

Optimizations

Processes For GA

notts 7.34 7.62

carf92 4.49 5.18

cars91 5.19 6.03

earf83 37.57 45.08

hecs92 11.47 12.90

kfus93 14.36 17.27

lsef91 11.90 15.11

purs93 4.88 5.57

ryef92 9.8 10.63

staf83 158.25 161.13

tres92 8.74 9.86

utas92 3.58 4.01

utes92 27.37 29.35

yorf83 41.10 43.52

However, the good cost obtained through the

experiment with GA did not manage to outperform

the results obtained by utilizing our proposed greedy

HC. Although the computational time taken by GA

execution is very much lower than HC, but an

additional reasonable amount of time taken to obtain

HillClimbingversusGeneticAlgorithmOptimizationinSolvingtheExaminationTimetablingProblem

249

qood quality schedules is considered very worth

while. Since HC managed to improve the initial

feasible schedule without fail for all datasets and

always surpass the GA results, therefore it is

suggested that the proposed HC is incorporated and

used in our whole set of optimization process.

Through the findings of this research, it makes it

more understandable to us the claim made by (Ross

et al., 1998) that sometimes GA is not a very good

approach in solving problems.

In the future work, we will try to implement

other types of search procedures to be incorporated

with our proposed method for example the Late

Acceptance Hill Climbing method which has been

proven to be very effective in producing

encouraging results to the examination scheduling

problem. (Bykov et al., 2008); (Bykov et al., 2009).

REFERENCES

A. J. Abramson D. 1992. A parallel genetic algorithm for

solving the school timetabling problem.

Asmuni H., E. K. Burke, J. M. Garibaldi, and Barry

McCollum. 2005. Fuzzy Multiple Heuristic Orderings

for Examination Timetabling. In E. K. Burke and M.

Trick, editors, Practice and Theory of Automated

Timetabling V (PATAT 2004, Pittsburg USA, August

2004, Selected Revised Papers), volume 3616 of

Lecture Notes in Computer Science, pages 334–353,

Berlin, 2005.Springer.

Asmuni H, E. K. Burke, J. M. Garibaldi, B. McCollum

and A. J. Parkes. 2009. An investigation of fuzzy

multiple heuristic orderings in the construction of

university examination timetables. Comput. Oper.

Res.,vol. 36, pp. 981-1001, 2009.

Bargiela, A. Pedrycz, W., 2008. Toward a theory of

Granular Computing for human-centred information

processing. IEEE Trans. on Fuzzy Systems, vol. 16, 2,

2008, 320-330, doi:10.1109/TFUZZ.2007.905912.

Bykov Y., Burke E. K. 2008. A late acceptance strategy in

hill-climbing for exam timetabling problems. PATAT

2008 Conference. Montreal, Canada.

Bykov Y., E. Ozcan, M. Birben. 2009. Examination

timetabling using late acceptance hyper-heuristics.

IEEE Congress on Evolutionary Computation.

Burke E. K., Elliman D. G., and Weare R. F. 1994a. A

Genetic Algorithm for University Timetabling. AISB

Workshop on Evolutionary Computing, University of

Leeds, UK.

Burke E. K., Elliman D. G., and Weare R. F. 1994b. A

Genetic Algorithm Based University Timetabling

System. AISB Workshop on Evolutionary Computing,

University of Leeds, UK.

Burke E. K., Bykov Y., Newall J. and Petrovic S. 2004. A

Time-Predefined Local Search Approach to Exam

Timetabling Problems. IIE Transactions on Operations

Engineering, 36(6) 509-528.

Burke E. K., Pham N, Yellen J. 2010c. Linear

Combinations of Heuristics for Examination

Timetabling. Annals of Operations Research DOI

10.1007/s10479-011-0854-y.

Carter M. and Laporte G. 1995. Recent developments in

practical examination timetabling. Lecture Notes in

Comput. Sci., vol 1153, pp.1-21, 1996 [Practice and

Theory of Automated Timetabling I, 1995].

Carter M., Laporte G. and Lee S. 1996. Examination

Timetabling: Algorithmic Strategies and Applications.

Journal of Operations Research Society, 47 373-383.

Dowsland K. A. and Thompson J. 2005. Ant colony

optimization for the examination scheduling problem.

Journal of Operational Research Society, 56: 426-438.

Gueret,. Narendra Jussien, Patrice Boizumault, Christian

Prins. 1995. Building University Timetables Using

Constraint Logic Programming. First International

Conference on the Practice and Theory of Automated

Timetabling, PATAT’ 95, pp. 393-408, Edinburgh.

Gyori S., Z. Petres, and A. Varkonyi-Koczy. Genetic

Algorithms in Timetabling. A New Approach. 2001.

Budapest University of Technology and Economics,

Department of Measurement and Information Systems.

Qu. R, Burke E. K., B. McCollum, L. T. G. Merlot, and S.

Y. Lee. 2009. A Survey of Search Methodologies and

Automated System Development for Examination

Timetabling. Journal of Scheduling, 12(1): 55-89,

2009. doi: 10.1007/s10951-008-0077-5.

Rahim, S. K. N. A., Bargiela, A., & Qu, R. 2009. Granular

Modelling Of Exam To Slot Allocation. ECMS 2009

Proceedings edited by J. Otamendi, A. Bargiela, J. L.

Montes, L. M. Doncel Pedrera (pp. 861-866).

European Council for Modeling and Simulation.

doi:10.7148/2009-0861-0866.

Rahim, S. K. N. A., Bargiela, A., & Qu, R. 2012. Domain

Transformation Approach to Deterministic

Optimization of Examination Timetables. Accepted

for publication in Artificial Intelligence Research

(AIR) Journal. Sciedu Press.

Ross P., Hart E. and Corne D. 1998. Some observations

about GA-based exam timetabling. In: E.K. Burke and

M.W. Carter (eds) (1998). Practice and Theory of

Automated Timetabling: Selected Papers from the 2nd

International Conference. Springer Lecture Notes in

Computer Science, vol. 1408. 115-129.

Taufiq Abdul Gani, Ahamad Tajudin Khader and Rahmat

Budiarto. 2004. Optimizing Examination Timetabling

using a Hybrid Evolution Strategies. IN: Proceedings

of the Second International Conference on

Autonomous Robots and Agents (ICARA 2004), 13-

15 December 2004, Palmerston North, New Zealand,

pp. 345-349.

Ulker O., Ozcan E. and E. E. Korkmaz. 2007. Linear

linkage encoding in grouping problems: applications

on graph coloring and timetabling. In: E.K. Burke and

H. Rudova (eds) (2007) Practice and Theory of

Automated Timetabling: Selected Papers from the 6th

International Conference. Springer Lecture Notes in

Computer Science, vol. 3867, 347-363.

ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems

250