Simple, Fast, Accurate Melanocytic Lesion Segmentation

in 1D Colour Space

F. Peruch

, F. Bogo

, M. Bonazza

, M. Bressan

, V. Cappelleri

and E. Peserico

Dip. Ing. Informazione, Univ. Padova, Padova, Italy

Dip. Medicina, Univ. Padova, Padova, Italy

Keywords:

Segmentation, Dermatoscopy, Melanoma, Melanocytic Lesion, Naevus.

Abstract:

We present a novel technique for melanocytic lesion segmentation, based on one-dimensional Principal Com-

ponent Analysis (PCA) in colour space. Our technique is simple and extremely fast, segmenting high-

resolution images in a fraction of a second even with the modest computational resources available on a

cell phone – an improvement of an order of magnitude or more over state-of-the-art techniques. Our technique

is also extremely accurate: very experienced dermatologists disagree with its segmentations less than they

disagree with the segmentations of all state-of-the-art techniques we tested, and in fact less than they disagree

with the segmentations of dermatologists of moderate experience.

1 INTRODUCTION

Malignant melanoma is an aggressive form of skin

cancer whose incidence is steadily growing world-

wide (Rigel et al., 1996). Early diagnosis promptly

followed by excision is crucial for patient survival.

Unfortunately, in its early stages malignant melanoma

appears very similar to a benign melanocytic lesion

(a common mole). However, malignant melanoma

can often be recognized even in its early stages by

a trained dermatologist, particularly when observed

through a dermatoscope – an instrument providing

magniﬁcation and speciﬁc illumination.

The ﬁrst step in the visual analysis of a

melanocytic lesion is segmentation, i.e. classiﬁcation

of all points in the image as part of the lesion or of

the surrounding, healthy skin. While segmentation is

typically studied in the context of automated image

analysis, it is a ﬁrst, necessary step even for human

operators who plan to evaluate quantitative features of

a lesion such as diameter or asymmetry – e.g. in the

context of epidemiological studies correlating those

features to lesion benignity (Stolz et al., 1994).

The most important aspect of a segmentation tech-

nique is accuracy. Accuracy is usually evaluated in

terms of divergence from the segmentation provided

by one or more human “experts”. The most widely

used metric is simply the number of misclassiﬁed pix-

els normalized over the size of the lesion (Joel et al.,

2002). A crucial observation is that even expert der-

matologists differ in their assessment of a lesion’s

border (see Figure 1), since lesions are often fuzzy

and there exists no standard operative deﬁnition of

whether a portion of skin belongs to a lesion or not

– dermatologists rely on subjective judgement devel-

oped over years of dermatoscopic training. The area

of the disagreement region is typically 10 − 20% of

the area of the lesion itself (Silletti et al., 2009; Bel-

loni Fortina et al., 2011); this is obviously the mini-

mum divergence that an automated system can be ex-

pected to have when evaluated against human experts.

Figure 1: A dermatoscopically imaged melanocytic le-

sion (left) and two widely divergent segmentations obtained

from two experienced dermatologists (right).

The second crucial aspect of an automated seg-

mentation technique is its computational efﬁciency.

A slow segmentation slows down any system based

on it, meaning such a system cannot be used by a

dermatologist performing real-time diagnosis. This

191

Peruch F., Bogo F., Bonazza M., Bressan M., Cappelleri V. and Peserico E..

Simple, Fast, Accurate Melanocytic Lesion Segmentation in 1D Colour Space.

DOI: 10.5220/0004289601910200

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 191-200

ISBN: 978-989-8565-47-1

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

is particularly important for hand-held, portable sys-

tems operating with limited computational resources.

This work presents a novel technique for the au-

tomated segmentation of dermatoscopically imaged

melanocytic lesions. Our technique is extremely ac-

curate: very experienced dermatologists disagree with

its results less than they disagree with those of derma-

tologists of moderate experience. It is also extremely

fast, segmenting high-resolution images in a fraction

of a second even with the modest computational re-

sources available on a cell phone – an order of magni-

tude faster than the fastest techniques in the literature.

The rest of this work is organized as follows. Sec-

tion 2 provides a brief review of the state of the art

on melanocytic lesion segmentation. Section 3 intro-

duces our novel approach, based on one-dimensional

Principal Component Analysis (PCA) of the colour

space of the image. Section 4 presents an experimen-

tal comparison of our technique with other segmen-

tation approaches, in terms of accuracy and computa-

tional efﬁciency. Finally, Section 5 summarizes our

results and discusses their signiﬁcance.

2 RELATED WORK

Numerous methods have been proposed for lesion

segmentation in dermatoscopic images. According

to a classiﬁcation commonly adopted in image seg-

mentation (Szeliski, 2010), we can separate them into

three main classes.

The ﬁrst class aims at identifying lesion bound-

aries by use of edges and smoothness constraints.

A good representative of this class is GVF Snakes

(Erkol et al., 2005). The accuracy in border identiﬁ-

cation may strongly depend on an initial segmentation

estimate, on effective preprocessing (e.g. for hair re-

moval) and on morphological postprocessing (Celebi

et al., 2009; Silveira et al., 2009).

The second class includes “split and merge” tech-

niques. These approaches proceed either by recur-

sively splitting the whole image into pieces based on

region statistics or, conversely, merging pixels and re-

gions together in a hierarchical fashion. Represen-

tatives of this class include Modiﬁed JSEG (Celebi

et al., 2007), Stabilized Inverse Diffusion Equations

(SIDE) (Gao et al., 1998), Statistical Region Merg-

ing (SRM) (Celebi et al., 2008), Watershed (Wang

et al., 2010). These algorithms are very sensitive to

correct tuning of a large number of parameters, lead-

ing to highly variable performance (Gao et al., 1998;

Silletti et al., 2009).

The third class of segmentation techniques for

melanocytic lesions discriminates between lesion and

healthy skin on the image’s colour histogram. Af-

ter a preprocessing phase, these approaches classify

each colour as healthy skin or lesional tissue. This

separation is mapped back onto the original image,

from which morphological postprocessing then elim-

inates small, spurious “patches”. Representatives of

this class include Mean-shift (Melli et al., 2006)

and Fuzzy c-means (Schmid, 1999; Cucchiara et al.,

2002; Silletti et al., 2009). Our approach belongs to

this third class.

3 A FIVE-STAGE TECHNIQUE

Our technique proceeds in ﬁve stages.

The ﬁrst stage (Subsection 3.1) is optional and

simply preprocesses the image with an automated hair

removal software. The second stage (Subsection 3.2)

performs a Principal Component Analysis (PCA) of

the colour histogram and reduces the dimensional-

ity of the colour space to 1. The third stage (Sub-

section 3.3) applies a blur ﬁlter to the image pro-

jected on the 1D space, in order to reduce noise. The

fourth stage (Subsection 3.4) separates the pixels into

two clusters, segmenting the image into regions cor-

responding to lesional and healthy skin. The ﬁfth and

ﬁnal stage (Subsection 3.5) morphologically postpro-

cesses the image to remove spurious “patches” and to

identify lesional areas of clinical interest.

3.1 Preprocessing

The presence of hair represents a common obstacle

in dermatoscopic analysis of melanocytic lesions. Al-

though our approach is relatively resilient to the pres-

ence of hair (see Section 4), in some cases automated

hair removal signiﬁcantly improves the ﬁnal result.

Thus, when necessary, we perform automated hair re-

moval with VirtualShave (Fiorese et al., 2011).

3.2 PCA in Colour Space

PCA (Abdi and Williams, 2010) is a standard mathe-

matical tool for statistical analysis of observations in

a multi-dimensional space.

We employ PCA to cluster the colours of the im-

age into two classes according to their projection on

the ﬁrst principal component of the colour histogram

(where each point in the RGB space has a “mass”

equal to the number of pixels with that colour). Using

only one dimension runs against the common wisdom

of melanocytic lesion segmentation through PCA: all

work in this area suggested one should use not only

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

192

the ﬁrst, but also the second principal component of

the colour histogram.

In practice, we perform PCA on an m-pixel RGB

image in four steps. First, we compute the mean R,

G and B values of the image – the barycentre of the

colour histogram. Then, we compute the 3 × 3 au-

tocorrelation matrix C = M

M, where the i

row

= hr

i of the m × 3 matrix M represents the

three colour components of the i

pixel, each compo-

nent normalized by subtracting the mean value of that

colour in the image. Effectively we have:

C =

∑

(1)

so that C can be easily computed by “streaming” the

image pixel by pixel, subtracting the mean R, G, and

B values, computing the 6 distinct products of the

pixel’s colour components, and adding each of those

products to the corresponding product for all other

pixels (note that C is characterized by 6 elements

rather than 9 since it is symmetrical).

Then, we compute the eigenvectors of C and take

the dominant one, i.e. the ﬁrst principal component

of M. This takes a negligible amount of time since

it only requires computing the roots of a 3

degree

polynomial (the characteristic polynomial of C) and

inverting a 3× 3 matrix.

Finally, we project each row of M onto the princi-

pal component obtaining a one channel grayscale im-

age. Again, this can be achieved by “streaming” the

image and performing only a few arithmetic opera-

tions for each pixel. Thus, the cost of the whole pro-

cedure is essentially that of scanning the image from

main memory three times (once for the average, once

for the covariance, once for the projection).

We noticed an extreme similarity between the

dominant eigenvectors of different melanocytic lesion

images. In a set of 60 images of different lesions from

different patients, for any pair of dominant eigenvec-

tors v and u, we found |v · u| > 0.99.

We then decided to experiment with a simpliﬁed

version of our technique, where instead of comput-

ing all eigenvectors of each image, one simply takes

the (precomputed) average of the ﬁrst eigenvector of

a small “training set” of images. Throughout the rest

of the article, we refer to this simpliﬁed version as

static 1D-PCA. Section 4 shows that this crude ap-

proximation still yields surprisingly good results and,

by completely bypassing the PCA portion of the com-

putation, allows signiﬁcant speedups.

Static 1D-PCA has another important advantage.

Since the 1D colour space on which the image is pro-

jected is independent of the image, one could utilize

the simpliﬁed technique with (cheaper) grayscale im-

age acquisition equipment paired with an appropri-

ately tuned (physical) colour ﬁlter. This could allow

considerable cost savings when developing biomedi-

cal equipment to e.g. evaluate size, growth patterns or

asymmetry of melanocytic lesions.

3.3 Noise Reduction

In order to reduce noise, we blur the grayscale im-

age corresponding to the projection on the ﬁrst princi-

pal component. More precisely, we replace the value

of each pixel with the average colour in the 11 × 11

pixel square surrounding it. This ﬁlter provides re-

sults comparable to those of a Gaussian ﬁlter, but is

far more computationally efﬁcient, requiring a single

scan of the image and no ﬂoating point operations.

3.4 Colour Clustering

Operating on the colour histogram h(·) that associates

to each colour c the number of pixels h(c) of that

colour, we separate colours (and thus pixels) into two

clusters corresponding respectively to healthy skin

and lesional tissue. This stage can be divided into a

preprocessing phase and two main phases.

The preprocessing applies to the histogram a

square root operator, followed by a moving average

operator over a window of 11 points. More precisely,

we have:

(x) =

h(x) h

(x) =

x+5

∑

y=x−5

(y) (2)

The square root operator enhances smaller val-

ues, which is useful when the percentages of healthy

skin and lesional tissue differ widely. The averaging

smooths out small ﬂuctuations.

The second phase clusters colours in two steps.

First we ﬁnd the positions M

of two local max-

ima in h

(·) that can be assumed as “centres” of, re-

spectively, the lesion cluster and the healthy skin clus-

ter. Then, we determine a frontier point F ∈ [M

]

separating the two clusters in the histogram.

The position M

of the ﬁrst cluster centre corre-

sponds to the position of the global maximum in h

(·)

(see Figure 2). This cluster cannot be classiﬁed as le-

sion or healthy skin until the second centre position

is found: lesion area may be larger or smaller than

healthy skin area. The second cluster centre M

computed as:

= argmax



(x)(h

) − h

))



, x 6= M

(3)

where h

) is the minimum of h

(·) between x

and M

. The two terms in the product being max-

imized (h

(x) and h

) − h

)) are meant to

Simple,Fast,AccurateMelanocyticLesionSegmentationin1DColourSpace

193

Figure 2: Identiﬁcation of clusters centres M

and M

in the

colour histogram.

favour, in the choice of M

, a colour that is “well-

represented” (yielding a high h

(x)) and at the same

time is “sharply separated” from M

(yielding a high

) − h

)). Remembering that lesional skin is

darker than healthy skin, M

and M

are then:

= min(M

), M

= max(M

) (4)

Finally, we choose the separation point between

skin colour and lesion colour as:

F = argmax



) − h

(x)





x − M

− M



(5)

where γ ∈ R

is the single “tuning” parameter of our

technique – the smaller γ, the “tighter” the segmenta-

tions produced. Informally, the ﬁrst term in the prod-

uct favours, as a separation point, a colour that is not

well-represented and that thus yields a sharp sepa-

ration between the two clusters. The second term,

whose weight grows with γ, favours a colour closer

to that of healthy skin; this attempts to reproduce the

behaviour of human dermatologists, who tend to clas-

sify as lesion regions of the image that are slightly

darker than the majority of the healthy skin, even

when those regions are considerably lighter than the

“core” of the lesion. Figure 3 illustrates how the clus-

tering results vary as γ increases from 0.8 to 1. On

our dataset, we obtained good results for all values of

γ in [1,1.4]. Note that the fractional exponentiation in

equation 5 is carried out at most once for each of the

256 points of the colour histogram, incurring an over-

all computational cost that is virtually negligible (see

Section 4).

Figure 3: Identiﬁcation of the separation point between

skin colour and lesion colour for γ = 1 (green) and γ = 0.8

(black). Higher values of γ favour colours closer to that of

healthy skin.

3.5 Postprocessing

Mapping the segmentation from colour space back

onto the original image produces a binary mask,

where each pixel is classiﬁed as lesional or healthy.

The postprocessing stage makes this classiﬁcation

more accurate. First, it corrects several local artefact

“patches” due to a pixel in the image being slightly

darker or lighter than its neighbours. Second, it iden-

tiﬁes all the connected components that, although

classiﬁed as healthy, are entirely surrounded by le-

sional pixels; these components usually correspond to

large air bubbles or regressions in a pigmented lesion,

and should therefore be classiﬁed as lesional.

Our postprocessing involves two phases (see Fig-

ure 4). We ﬁrst “downsample” the image in order to

easily identify the boundaries of each lesional compo-

nent through a simpliﬁed (and faster!) version of the

technique described in (Suzuki et al., 2003). Then,

we remove all boundaries delimiting connected com-

ponents that are “too small”. We now describe each

phase in greater detail.

Denote by p

i j

the pixel located at row i and col-

umn j in an image, and by v(p

i j

) its value. For any

pixel, we consider its 4-way and 8-way neighbour-

hood – informally, the 4 pixels adjacent to it hori-

zontally or vertically, and the 8 pixels adjacent to it

horizontally, vertically or diagonally. More formally,

for each internal (i.e. non-edge and non-corner) pixel

i j

of an image:

Deﬁnition 1. The 4-way neighbourhood of p

i j

con-

sists of the 4 pixels p

such that |i − k| + |l − j| = 1.

Deﬁnition 2. The 8-way neighbourhood of p

i j

con-

sists of the 8 pixels p

6= p

i j

such that |i − k| ≤ 1 and

|l − j| ≤ 1.

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

194

(a) (b)

(e)

Figure 4: The postprocessing stage. (a) Initial binary mask.

(b) Binary mask after downsampling. (c) Boundary pix-

els. (d) D-rows. (e) Single boundary encircling “sufﬁcient”

area.

We deal with pixels on the edges or corners of the

image by surrounding the image with a 1-pixel-wide

strip of non-lesional pixels so that the pixels of the

original image correspond to the internal pixels of the

expanded image.

In the downsampling phase, we partition the (ex-

panded) image into boxes of 3 × 3 pixels; each pixel

in a box takes the value of the central pixel in the box:

v(p

i j

) , v(p

) with k = 3





+ 1 , l = 3





+ 1

(6)

Then, we identify the boundary pixels in the image:

Deﬁnition 3. A boundary pixel is a lesional pixel

whose 4-way neighbourhood contains exactly 3 le-

sional pixels.

It would be tedious but straightforward to ver-

ify that, due to the downsampling phase, the 8-way

neighbourhood of any boundary pixel contains ex-

actly 2 boundary pixels.

If we consider any boundary pixel as a vertex of

degree 2 connected by an edge to its two adjacent

boundary pixels, then we obtain a set of disjoint cy-

cle graphs in the image, corresponding to the actual

boundaries of all (putative lesional) connected com-

ponents. This makes it extremely easy to “walk” a

boundary, starting from any of its pixels, following

the edges between adjacent vertices. Note that, up

to this stage, no explicit label has been assigned to

any pixel since those satisfying the boundary deﬁni-

tion are simply marked as “boundary pixels” without

any distinction between different contours; this is the

crucial simpliﬁcation of our scheme compared to that

of (Suzuki et al., 2003).

In the second step, we compute the area of all con-

nected components of “sufﬁcient” height – we can ex-

pect a minimum height for any lesion of clinical inter-

est of 5% of the image’s height. More formally:

Deﬁnition 4. Consider an image of r rows, numbered

from 1 to r starting from the top, and a parameter

d (1 ≤ d ≤ r). We say the i

row is a d-row if i

mod d = 0.

Only boundary pixels belonging to a d-row serve

as “starting points” to follow the corresponding

boundary. From the boundary, we can easily obtain

the area of the connected component, as follows. Let

be the i

boundary pixel of the connected compo-

nent on a generic row; then the pixels of the connected

component in that row are those between any two con-

secutive boundary pixels b

and b

i+1

with i odd.

Every component with height at least d is

“caught” by our technique, while smaller components

may be missed (if no d-row intersects them) – but

these “small” components are of no interest to us.

d-rows allow considerable speedups as long as d is

larger than 5− 10; while d values equal to (or smaller

than) 5% of the image’s height catch all lesions of

clinical interest. Thus, we set d as 5% of the image’s

height.

In the last step, all boundaries delimiting areas

smaller than one ﬁfth that of the largest connected

component are removed. This takes care of both small

dark patches in healthy skin, and small light patches

within a lesion.

Note that, even if there are many known tech-

niques to identify connected components in a binary

image (Chang et al., 2004; Park et al., 2000; Martin-

Herrero, 2007), they are not suitable for our purposes.

Classic techniques (Chang et al., 2004; Park et al.,

2000) are in general computationally expensive, re-

quiring at least two scans of the image and/or the in-

troduction of additional data structures; in contrast,

our technique requires a single sequential pass plus a

small number of additional accesses to a limited num-

ber of image pixels. Even the optimized, single-pass

approach of (Martin-Herrero, 2007) requires approx-

imately 30% more time than ours; and requires addi-

tional effort to “match” portions of the lesion or of the

skin that do not belong to the same connected compo-

nent.

Simple,Fast,AccurateMelanocyticLesionSegmentationin1DColourSpace

195

4 EXPERIMENTAL EVALUATION

We evaluated our segmentation technique by compar-

ing it to three different state-of-the-art techniques. Af-

ter brieﬂy describing our experimental setup (Subsec-

tion 4.1), we present the evaluation results in terms

of both accuracy (Subsection 4.2) and computational

efﬁciency (Subsection 4.3).

4.1 Experimental Setup

60 images of melanocytic lesions were acquired at

768 × 576 resolution using a Fotoﬁnder digital

dermatoscope (FotoFinder Systems Inc., 2012). 12

copies of each image were printed on 13cm × 18cm

photographic paper. A copy of each image and a spe-

cial marker pen were given to each of 4 “junior”, 4

“senior” and 4 “expert” dermatologists (having re-

spectively less than 1 year of experience, more than 1

year but no dermatoscopic training, more than 1 year

and dermatoscopic training). Each dermatologist was

then asked to independently draw with the marker the

border of each lesion. The images (and borders) were

scanned and realigned to the same frame of reference.

Finally, the contours provided by the markers were

extracted and compared. This allowed the identiﬁca-

tion, for each pixel of each original image, of the set

of dermatologists classifying it as part of the lesion or

of the surrounding, healthy skin.

We developed a Java implementation of our seg-

mentation technique. In order to evaluate its efﬁ-

ciency on a wide range of devices, from desktops to

hand-helds, we tested it on three different platforms:

a Samsung Galaxy S cell phone with a 1 GHz ARM

Cortex A8 processor, an ASUS Transformer Prime

tablet with a 1.3 GHz Nvidia Tegra 3 processor, and a

desktop PC with a 3.07 GHz Intel Core i7-950 proces-

sor. To provide a clearer evaluation of the strengths

and limitations of our technique, none of our tests

made use of the optional digital hair removal phase

(see Subsection 3.1).

We compared our technique with three differ-

ent state-of-the-art approaches, selecting a represen-

tative technique for each of the three classes in-

troduced in Section 2. We chose techniques with

publicly available implementations. For the ﬁrst

class, we considered the EdgeFlow algorithm (Ma

and Manjunath, 2000) (http://vision.ece.ucsb.

edu/segmentation/edgeflow/software). Recent

work (Celebi et al., 2009; Silveira et al., 2009) has

already shown how simple active contours methods

(like GVF Snakes) perform quite poorly in terms of

accuracy; we therefore chose to test a method, like

EdgeFlow, which aims at detecting edges more ro-

bustly – unifying the active contour model with tex-

ture segmentation techniques. For the second class,

we tested the Statistical Region Merging (SRM) algo-

rithm (Celebi et al., 2008). For the third class, we

implemented a Java version of the 2D-PCA algorithm

proposed in (Silletti et al., 2009).

SRM does not work properly on lesions adjacent

to the image’s borders. Thus, for its evaluation, we re-

moved from our dataset all such images, testing it on a

reduced dataset of 40 images. Our own technique pro-

duces more accurate segmentations on this reduced

dataset than on the full one (see Subsection 4.2) so

we effectively gave SRM an advantage by allowing it

to run on an “easier” dataset.

EdgeFlow produces a set of segmented regions,

but does not include a decisional step to determine

which regions should be marked as part of the lesion.

Again, we chose to make the comparison as biased as

possible against our own technique, allowing Edge-

Flow a perfect, instantaneous decisional step. More

precisely, we assumed the decisional step would take

zero time, and would choose as output for EdgeFlow

the set of regions maximizing the segmentation accu-

racy (see Figure 5 and the following Subsection).

Figure 5: Melanocytic lesion segmentation using Edge-

Flow. White contours identify the output of the algorithm.

Blue contours identify the area considered lesional in our

evaluation of EdgeFlow.

4.2 Accuracy

We measured the accuracy of a generic segmenta-

tion S by comparing it to a “ground truth” reference

segmentation R, and counting the number TP of true

positive pixels (classiﬁed as lesion by both segmen-

tations), the number FP of false positive pixels (clas-

siﬁed as lesion by S but not by R), the number FN

of false negative pixels (classiﬁed as lesion by R but

not by S) and the number TN of true negative pix-

els (classiﬁed as lesion by neither segmentation). We

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

196

Expert Senior

Junior 1D-PCA

Figure 6: Melanocytic lesion segmentation performed by

human dermatologists and 1D-PCA.

Expert SRM

EdgeFlow 1D-PCA

Figure 7: Melanocytic lesion segmentation performed by

expert dermatologists, SRM, EdgeFlow and 1D-PCA.

then computed the divergence of S from R as:

FP + FN

T P + FN

i.e. as the ratio between the area of the misclassi-

ﬁed region (FP+FN) and the area of the lesion itself

according to the ground truth reference segmentation

(TP+FN) (Hance et al., 1996).

We evaluated the different techniques by compar-

ing their segmentations with those produced by the

4 expert dermatologists (see Table 1). 1D-PCA ob-

tained, on average, a 12.35% divergence from expert

dermatologists. In the spirit of (Silletti et al., 2009),

we also evaluated the 4 senior and 4 junior derma-

tologists using as ground truth the segmentations pro-

duced by the 4 expert dermatologists, and each expert

Table 1: Divergence d

(average and standard deviation)

from expert dermatologists in the segmentation performed

by different dermatologists and automated techniques. For

the SRM algorithm, results refer to the reduced dataset (40

images).

Group d

(avg) d

(std)

Experts 10.40% 6.86%

Seniors 13.57% 9.54%

Juniors 17.24% 15.53%

1D-PCA 12.35% 6.98%

1D-PCA static 12.45% 7.16%

1D-PCA static w/o NR 13.44% 8.21%

2D-PCA 15.58% 7.19%

SRM 15.15% 8.65%

EdgeFlow 16.75% 8.06%

dermatologist using as ground truth the segmentations

produced by the remaining 3 expert dermatologists.

The average divergence of junior dermatologists from

the experts, of the senior dermatologists from the ex-

perts, and of the experts from the other experts, was

respectively 17.24%, 13.57% and 10.40%.

Thus, our 1D-PCA technique achieved a disagree-

ment with expert dermatologists that was lower than

that achieved by junior and senior dermatologists, and

very close to the disagreement of expert dermatolo-

gists between themselves (see Figure 6). This makes

it essentially optimal in terms of accuracy, since dis-

agreement between experts can be viewed as an in-

trinsic, inevitable level of “noise” in the evaluation of

melanocytic lesion border (Silletti et al., 2009).

Quite surprisingly, we observed that some simpli-

ﬁcations applied to 1D-PCA lead to only modest re-

ductions in accuracy. Using the simpliﬁed static 1D-

PCA (Section 3.2) resulted in a negligible 0.1% loss

in accuracy; eliminating the noise reduction step (see

Subsection 3.3) similarly produced a very small loss

in accuracy – only 1% (see Table 1). As we shall

see in the following Subsection, these small accuracy

losses can be traded for fairly signiﬁcant speedups.

All other automated techniques exhibited worse

accuracy. EdgeFlow provided the worst results, with

an accuracy comparable to that of junior dermatol-

ogists, despite our “generous” evaluation which, for

each image, considered lesional the set of regions

minimizing divergence from the ground truth (see

Subsection 4.1). The accuracy of SRM, too, was

worse than that of senior dermatologists, again de-

spite a “generous” evaluation on the easier, reduced

dataset (by means of comparison, our technique im-

proved its divergence from 12.35% to 11.87% when

moving from the full dataset to the reduced one). Per-

haps most surprisingly, even 2D-PCA was less accu-

rate than 1D-PCA; this difference may be due in part

to the fact that the second principal component intro-

Simple,Fast,AccurateMelanocyticLesionSegmentationin1DColourSpace

197

duces more noise than information, and in part to the

fact that operating on a 1D colour histogram allows

one to take a slightly more sophisticated approach

to the identiﬁcation of the colour cluster centres and

boundaries.

As a ﬁnal note, we remark that our technique

is also extremely robust. Many of the photographs

exhibited a number of defects making segmentation

harder. 1D-PCA is surprisingly resistant to minor im-

perfections like small air bubbles in the anti-reﬂective

gel or shadows cast by the dermatoscope; we ob-

served an average divergence of only 11.09% on these

images (12 in total). However, images with many pix-

els occluded by dark hair, with large air bubbles cast-

ing deep shadows, or with incorrectly framed lesions

“overﬂowing” from the image, lead to larger diver-

gences (15.36% on average, on a total of 14 such im-

ages). While digital hair removal (Fiorese et al., 2011)

is a solution to the ﬁrst problem, the latter two clearly

stress the importance of taking good photographs in

the ﬁrst place.

4.3 Computational Resources

Our segmentation technique is extremely fast. Seg-

menting any one of our test images in memory took

less than 0.02 seconds on the Core i7 desktop and

only 0.7 seconds on the Galaxy S cell phone (this

does not account for the possible cost of preprocess-

ing with a hair-removing tool).

Tables 2 and 3 show how the execution time can be

further trimmed down by skipping some computation-

intensive operations that do not signiﬁcantly improve

the accuracy of the segmentation.

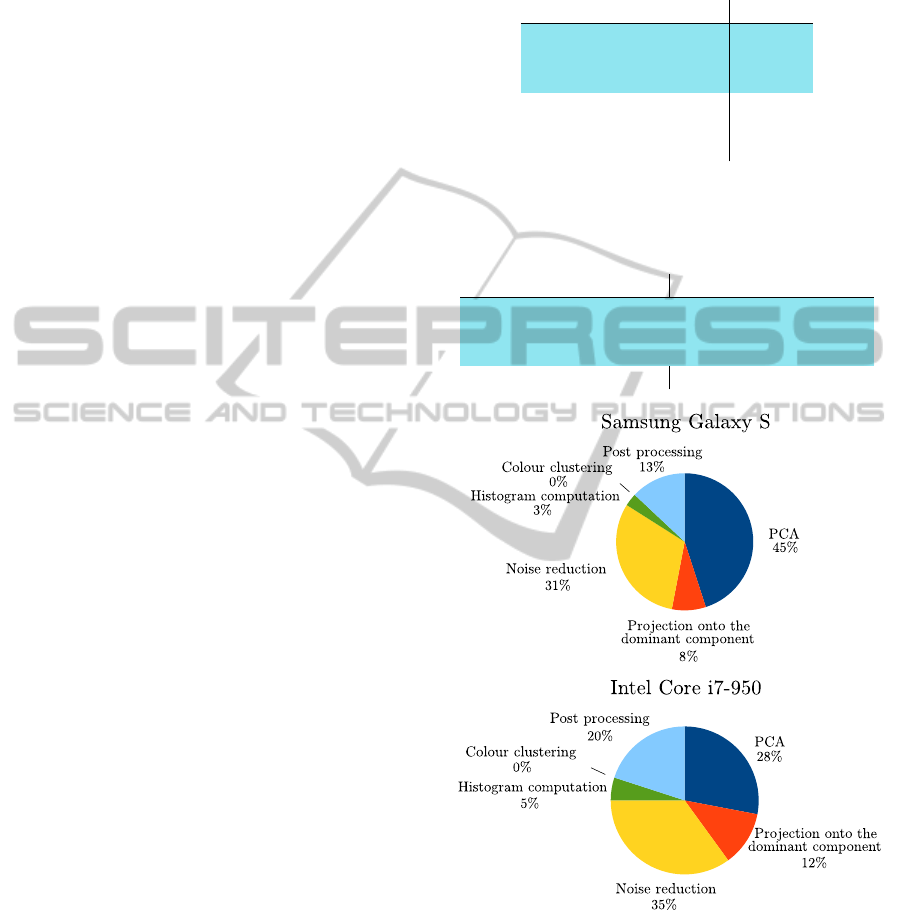
Static 1D-PCA required 30% less execution time

than 1D-PCA – while providing virtually identical

accuracy. Devices with lower computational power

beneﬁt even more from this simpliﬁcation: on the

the Galaxy S static 1D-PCA required 45% less time

than 1D-PCA. Similarly, skipping the noise reduc-

tion phase (and thus worsening accuracy by a mod-

est 1%) reduced execution time by 30 − 40% (and

by 50 − 55% in the case of static 1D-PCA). Figure

8 summarizes the computational costs of each phase.

In contrast with the (1D and 2D) PCA implemen-

tations, which are written in Java for portability, SRM

and EdgeFlow are written in C (generally more efﬁ-

cient). Thus, we could test them only on the Core i7

platform (see Table 2). 1D-PCA outperformed both

SRM and 2D-PCA by over an order of magnitude in

terms of running time; and EdgeFlow by several or-

ders of magnitude (even though we “charged” Edge-

Flow no time costs for the choice of the lesional re-

gion set – see Subsection 4.1).

Table 2: Execution time in milliseconds of 1D-PCA, static

1D-PCA with and without noise reduction, 2D-PCA, SRM

and EdgeFlow on a desktop PC mounting an Intel Core i7-

950 processor.

Core i7

1D-PCA 17

1D-PCA static 12

1D-PCA static w/o NR 7

2D-PCA 199

SRM 189

EdgeFlow 104789

Table 3: Execution time in milliseconds of 1D-PCA, static

1D-PCA with noise reduction disabled or enabled and 2D-

PCA on a Samsung Galaxy S cell phone and on an ASUS

Transformer Prime tablet.

Galaxy Transformer

1D-PCA 733 411

1D-PCA static 407 286

1D-PCA static w/o NR 185 120

2D-PCA 5986 2778

Figure 8: Time cost breakdown of our technique on a Sam-

sung Galaxy S cell phone and on a desktop PC mounting an

Intel Core i7-950 processor.

The main reason for the extreme computational

performance of 1D-PCA is the fact that the 1D colour

histogram can be processed extremely quickly: only a

handful of simple operations are required for each of

its 256 points, without any need of costly iterations.

And since PCA, colour histogram creation, and mor-

phological postprocessing all boil down to “stream-

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

198

ing” the image while performing a few simple opera-

tions on each of its pixels, the total cost of segmenting

the image is essentially that of scanning it a few times.

5 CONCLUSIONS

Our simple technique for melanocytic lesion segmen-

tation is extremely fast. A Java implementation of it

can segment a large dermatoscopic image in the time

required to simply scan the image a handful of times –

a fraction of a second even on hand-held devices with

modest computational resources. This represents an

improvement of an order of magnitude or more over

state-of-the-art techniques.

At the same time, our technique does not sacriﬁce

accuracy. It appears more accurate than state-of-the-

art techniques. Perhaps more importantly, it appears

almost as accurate as any segmentation technique can

be, since expert dermatologists disagree with it only

slightly more than they disagree between themselves

– and less than they disagree with dermatologists of

little, or even moderate, experience.

Finally, our technique is extremely robust. It does

not require careful hand-tuning; a single parameter

controls how “tight” the segmentation is. It tolerates

very well small photographic defects, such as small

air bubbles or uneven lighting. It is only slightly less

robust in the face of hair (which could be easily re-

moved, physically or through digital preprocessing),

larger air bubbles, or improper lesion framing. In fact,

our technique is so robust that one can achieve almost

as accurate results with a crude simpliﬁcation of it

which, instead of projecting the colour space of each

image onto its principal component, projects it onto a

precomputed space independent of the image – allow-

ing even faster processing, as well as use of (cheaper)

monochromatic image acquisition equipment.

ACKNOWLEDGEMENTS

This work was supported by Univ. Padova un-

der strategic project AACSE. F. Peruch, F. Bogo,

M. Bressan and V. Cappelleri were supported in part

by fellowships from Univ. Padova. The authors would

thank the Dermatology Unit of Univ. Padova for its

invaluable help.

REFERENCES

Abdi, H. and Williams, L. J. (2010). Principal component

analysis. WIREs Comp. Stat., 2(4).

Belloni Fortina, A., Peserico, E., Silletti, A., and Zattra, E.

(2011). Where’s the naevus? Inter-operator variability

in the localization of melanocytic lesion border. Skin

Res. and Tech., 18(3).

Celebi, M. E., Aslandogan, Y., and Van Stoecker, W.

(2007). Unsupervised border detection in dermoscopy

images. Skin Res. and Tech., 13(4).

Celebi, M. E., Iyatomi, H., Schaefer, G., and Stoecker, W. V.

(2009). Lesion border detection in dermoscopy im-

ages. Comput. Med. Imaging Graph., 33(2).

Celebi, M. E., Kingravi, H. A., Iyatomi, H., Aslandogan,

Y. A., Van Stoecker, W., Moss, R. H., Malters, J. M.,

Grichnik, J. M., Marghoob, A. A., Rabinovitz, H. S.,

and Menzies, S. W. (2008). Border detection in der-

moscopy images using statistical region merging. Skin

Res. and Tech., 14(3).

Chang, F., Chen, C.-J., and Lu, C.-J. (2004). A linear-time

component-labeling algorithm using contour tracing

technique. Comput. Vis. Image Underst., 93(2).

Cucchiara, R., Grana, C., Seidenari, S., and Pellacani, G.

(2002). Exploiting color and topological features for

region segmentation with recursive fuzzy c-means.

Machine Graph. and Vision, 11(2/3).

Erkol, B., Moss, R. H., Stanley, R. J., Van Stoecker, W.,

and Hvatum, E. (2005). Automatic lesion boundary

detection in dermoscopy images using gradient vector

ﬂow snakes. Skin Res. and Tech., 11(1).

Fiorese, M., Peserico, E., and Silletti, A. (2011). Virtual-

Shave: Automated hair removal from digital dermato-

scopic images. In Proc. of IEEE EMBC.

FotoFinder Systems Inc. (2012). Fotoﬁnder dermoscope.

http://www.fotoﬁnder.de/en.html.

Gao, J., Zhang, J., Fleming, M. G., Pollak, I., and Cognetta,

A. B. (1998). Segmentation of dermatoscopic images

by stabilized inverse diffusion equations. In Proc. of

ICIP.

Hance, G. A., Umbaugh, S. E., Moss, R. H., and Stoecker,

W. V. (1996). Unsupervised color image segmentation

with application to skin tumor borders. In Proc. of

IEEE EMBC.

Joel, G., Schmid-Saugeon, P., Guggisberg, D., Cerottini,

J. P., Braun, R., Krischer, J., Saurat, J. H., and Mu-

rat, K. (2002). Validation of segmentation techniques

for digital dermoscopy. Skin Res. and Tech., 8(4).

Ma, W.-Y. and Manjunath, B. S. (2000). EdgeFlow: a tech-

nique for boundary detection and image segmentation.

IEEE Trans. on Image Processing, 9(8).

Martin-Herrero, J. (2007). Hybrid object labelling in digital

images. Machine Vision and Applications, 18(1).

Melli, R., Grana, C., and Cucchiara, R. (2006). Compari-

son of color clustering algorithms for segmentation of

dermatological images. In Proc. of SPIE.

Park, J.-M., Looney, C. G., and Chen, H.-C. (2000). Fast

connected component labeling algorithm using a di-

vide and conquer technique. In Proc. of ISCA 15th

Conference on Computers and Their Applications.

Rigel, D. S., Friedman, R. J., and Kopf, A. W. (1996).

The incidence of malignant melanoma in the United

States: issues as we approach the 21st century. JAAD,

34(5, Part 1).

Simple,Fast,AccurateMelanocyticLesionSegmentationin1DColourSpace

199

Schmid, P. (1999). Segmentation of digitized dermato-

scopic images by two-dimensional color clustering

comparison. IEEE Trans. on Medical Imaging, 18(2).

Silletti, A., Peserico, E., Mantovan, A., Zattra, E., Peserico,

A., and Belloni Fortina, A. (2009). Variability in hu-

man and automatic segmentation of melanocytic le-

sions. In Proc. of IEEE EMBC.

Silveira, M., Nascimento, J., Marques, J., Marcal, A., Men-

donca, T., Yamauchi, S., Maeda, J., and Rozeira, J.

(2009). Comparison of segmentation methods for

melanoma diagnosis in dermoscopy images. Selected

Topics in Signal Processing, 3(1).

Stolz, W., Merkie, T., Cognetta, A., Vogt, T., Landthaler,

M., Bilek, P., and Plewig, G. (1994). The ABCD rule

of dermatoscopy. JAAD, 30(4).

Suzuki, K., Horiba, I., and Sugie, N. (2003). Linear-time

connected-component labeling based on sequential lo-

cal operations. Comput. Vis. Image Underst., 89(1).

Szeliski, R. (2010). Computer vision: algorithms and ap-

plications. Springer.

Wang, H., Chen, X., Moss, R. H., Stanley, R. J., Stoecker,

W. V., Celebi, M. E., Szalapski, T. M., Malters, J. M.,

Grichnik, J. M., Marghoob, A. A., Rabinovits, H. S.,

and Menzies, S. W. (2010). Watershed segmentation

of dermoscopy images using a watershed technique.

Skin Res. and Tech., 16(3).

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

200