Interactive Rendering of Complex 3D-Treemaps with a Comparative

Performance Evaluation

Matthias Trapp, Sebastian Schmechel and J

urgen D

ollner

Hasso-Plattner-Institut, University of Potsdam, Potsdam, Germany

Keywords:

3D-Treemaps, Real-time Rendering, Performance Evaluation.

Abstract:

3D-Treemaps are an important visualization technique for hierarchical views. In contrast to 2D-Treemaps,

height can be used to map one additional attribute of the data items. Using the Treemap technique in com-

bination with large datasets (more than 500k) a fast rendering and interaction techniques that are beyond

collapsing/uncollapsing nodes is still one of the main challenges. This paper presents a novel rendering tech-

nique that enables the image synthesis of geometrical complex 3D-Treemaps in real-time. The fully hardware

accelerated approach is based on shape generation using geometry shaders. This approach offers increased

rendering performance and low update latency compared to existing techniques and through it enables new

real-time interaction techniques to large datasets.

1 INTRODUCTION

Motivation The concept of treemaps is an im-

portant tool for visualization of large hierarchical

datasets. Its extension to the third dimension enables

a number of applications, like metaphor-based visual-

ization that support the user’s mental model creation

of abstract datasets and through it the memorability

of items as shown in InformationPyramids (Andrews

et al., 1997) and CodeCity (Wettel and Lanza, 2008).

However, the additional dimension comes with ad-

ditional concerning the geometric representation and

image-synthesis. In particular, this introduces chal-

lenges for the interactive rendering of complex 3D-

Treemaps. Complex 3D-Treemaps are described by a

large number of treemap items, e.g., more than 500k

(Fig. 1), and diverse attribute mappings to color and

height of these items.

Basically the interaction in 3D-Treemaps can be

grouped in three main tasks: (a) Navigational tasks

(e.g., Zooming and Panning), (b) Explorational tasks

(e.g., implicit and explicit visualization of nodes at-

tributes and informations), and (c) Data-Modiﬁcation

tasks (adding or removing nodes). While naviga-

tion and exploration tasks are independent from the

complexity of the underlying layout algorithm, Data-

Modiﬁcation tasks result in a recomputation of the

layout. Nevertheless the degree of user experience

for layout-independent tasks are highly connected to

the rendering run-time (Correa et al., 2003). Bladh

Figure 1: An example of a complex 3D-Treemap with

614k items rendered with the presented shape generation

approach in real-time. It comprises over six million render-

ing primitives.

et al. present a visualization techniques that support

interactive (real-time) image synthesis and allow nav-

igation and exploration tasks through animated transi-

tions (Bladh et al., 2005). In addition to that, a change

or update of mappings on rendered treemap artifacts,

require a high update performance.

Rendering of Complex 3D Scenes. To summarize,

despite the performance of the layout algorithm and

dynamic update of treemaps, the efﬁcient rendering

remains a challenge. The efﬁcient interactive render-

ing of complex 3D-Treemaps depends on the follow-

165

Trapp M., Schmechel S. and Döllner J..

Interactive Rendering of Complex 3D-Treemaps with a Comparative Performance Evaluations.

DOI: 10.5220/0004290101650175

In Proceedings of the International Conference on Computer Graphics Theory and Applications and International Conference on Information

Visualization Theory and Applications (GRAPP-2013), pages 165-175

ISBN: 978-989-8565-46-4

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

ing three aspects concerning the rendering techniques

as well as the underlying data representation:

Rendering Performance. The run-time complexity

for the rendering of a single frame must be small

enough to support interactive frame rates for a

high number of treemap items. The rendering per-

formance often depends on the geometric repre-

sentation of the datasets.

Update Performance. The update performance is

determined by the number of changes in treemap

representation required for a speciﬁc visualiza-

tion. Thus, increasing the update performance

contributes to the available per-frame rendering

budget.

Memory Consumptions. The memory consump-

tions (both in main and video memory) of a 3D-

Treemap representation determines the maximum

amount of 3D-Treemap items that can be rendered

without using out-of-core mechanisms, which in-

troduce additional IO operations and more com-

plex implementations. Therefore, the space com-

plexity of a representation should be as compact

as possible.

Thus, the main goals of a rendering technique that

facilitate the interactive rendering of complex 3D-

Treemaps are the reduction of rendering, update, and

storage costs.

Contributions. Concerning the challenges stated

above, this paper presents a novel, fully hardware-

accelerated rendering technique that is capable of per-

forming real-time image-synthesis for complex 3D-

Treemaps within a single rendering pass. The ap-

proach is based on server-side shape generation, i.e.,

the geometry of 3D-Treemap items is created on

graphics hardware. This reduces bandwidth and in-

creases uptime performance, as well as enables a

compact representation of a 3D-Treemap with a min-

imal memory footprint. Its implementation is based

on OpenGL and the OpenGL Shading Language (Se-

gal and Akeley, 2012); an API which is of broad use

within scientiﬁc visualization. The presented con-

cepts can also be transfered to D3D compatible ap-

plications. To summarize, this paper makes the fol-

lowing contributions to the community:

1. Presents a novel rendering technique especially

suitable for rendering complex 3D-Treemaps in

real-time. This technique is especially suitable for

interaction metaphors without recomputing the

treemap layout.

2. Describes the implementation of different concur-

rent rendering techniques for the interactive ren-

dering of complex 3D-Treemaps.

3. Evaluates and compares these rendering tech-

niques with respect to rendering performance, up-

date performance, and memory consumptions.

The remainder of this paper is structured as follows.

Section 2 reviews related and previous work with re-

spect to 3D-Treemaps and rendering approaches. Sec-

tion 3 describes the shape generation approach and

existing techniques suitable for the interactive render-

ing of complex for 3D-Treemaps. Section 4 gives

implementation details. Section 5 presents a perfor-

mance analysis and comparison of the rendering tech-

niques. Finally, Section 6 concludes the paper.

2 RELATED WORK

Treemaps are a common used technique for space-

restricted visualization in the last two decades. The

original algorithm presented by Shneiderman recur-

sively splits parent nodes alternating in horizontal and

vertical direction by their child nodes (Shneiderman,

1992). One major disadvantage of the Slice’n Dice

algorithm is the creation of unfavorable aspect ratios

of the node representations. Bruels et al. as well as

Bederson and Shneiderman counter the problem with

Squariﬁed- (Bruls et al., 2000) and Strip-Treemap

(Bederson et al., 2002) layouts. Fekete and Plaisant

use treemaps to visualize datasets with about one mil-

lion nodes. In addition to visualize the structure of the

hierarchy, the items’ attributes were also visualized

by mappings onto size and color (Fekete and Plaisant,

2002). The increasing number of items in large hier-

archies leads to perceptional questions about Treemap

visualizations, e.g., how much effect does the width of

a nodes’ border have on the ability to extract the hier-

archical structure of the underlying data (Kong et al.,

2010).

The ﬁrst extension of 2D-Treemap layout algo-

rithms to the third dimension are presented in the

StepTree by Bladh et al.. They extend the initial

algorithm by stacking the graphical representations

of subdirectories on top of its parent’s one (Bladh

et al., 2004). In a comparative study between the

StepTree and its corresponding 2D-Treemap users

signiﬁcantly performed better in tasks of interpretat-

ing the hierarchical structure, while preserving per-

formance in other interpretational and navigational

tasks. Wettel and Lanza use 3D-Treemaps to create

a metaphorical view on software system artifact hi-

erarchies with CodeCities (Wettel and Lanza, 2008)

by mapping additional information to the height of

leaf nodes. This leads to a treemap-based layout

with graphical representations of software system ar-

tifacts as high and low “buildings” grouped in areas

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

166

Figure 2: Comparison of different rendering pipelines for client-side (CPU) shape generation (top) and our server-side shape

generation (bottom).

of the “software city”. Several other publications ad-

dresses the use of 3D-Treemaps in Software Visual-

ization in depth (Liggesmeyer et al., 2009; Bohnet

and D

ollner, 2011). Bohnet and D

ollner also men-

tioned that the use of realistic rendering effects, e.g.,

shadowing, in 3D-Treemaps support the users’ per-

ception of the elements as distinguished ones (Bohnet

and D

ollner, 2011). All of the aforementioned pub-

lications uses 3D-Treemaps by extruding the nodes,

calculated with a 2D-layout algorithm, by one addi-

tional attribute mapping. In addition to this classical

approach there exist a variety of modiﬁcations and ex-

tensions, e.g., 3D-Polar Treemaps, Treecube or Col-

lector’s Box Treemap (Schulz et al., 2011), one can

categorize by four attributes (a) containment relation-

ship, (b) used graphics primitives, (c) layout method

and (d) alignment (Schulz et al., 2007).

Even though the visualization of a wide range

of large hierarchical datasets, e.g., software sys-

tems, economy data, is frequently studied, the inter-

action techniques used in this ﬁeld are straightfor-

ward. Appearing techniques in 3D-Treemaps are the

selection of nodes and leafs, as well as the color-

ing/highlighting of nodes (Wettel and Lanza, 2008).

Sud et al. present a solution to provide interactive

rendering, navigation and animation of dynamically

changing 2D-Voronoi-Treemaps by using a GPGPU-

based rendering technique (Sud et al., 2010).

With an increasing amount of nodes the geomet-

rical complexity of treemap grows directly, resulting

in the need of general computer graphical techniques

to create an interactive visualization. One way to

achieve a lower memory footprint and a faster ren-

dering is the algorithm for triangle strip optimization

shown by Evans et al. (Evans et al., 1996).

3 RENDERING TECHNIQUES

The rendering techniques in this paper is a combina-

tion of standard forward rendering and deferred shad-

ing (Liktor and Dachsbacher, 2012). Despite interme-

diate rendering (also know as the obsolete interme-

diate mode in former OpenGL speciﬁcations), three

types of techniques are suitable for the interactive ren-

dering of complex 3D-Treemaps: (1) using (indexed

and non-indexed) vertex buffer objects (Section 3.3),

geometry instancing variants (Section 3.4), as well as

a novel server-side shape generation approach (Sec-

tion 3.2).

For clariﬁcation, Figure 2 shows a comparison of

the different, simpliﬁed pipelines suitable for render-

ing geometrical complex 3D-Treemaps. The illustra-

tion on top shows classical forward rendering pipeline

as used for the existing rendering approaches. The ge-

ometry required for the rendering of 3D-Treemaps is

generated on the client side (CPU). This implies the

the generated geometry must be transfered to server

every time the representation changes, e.g., due to

changes in the layout or in the thematic mapping. We

denote this pipeline model as client-side shape gener-

ation. In contrast thereto, the illustration on the bot-

tom shows the rendering pipeline for the presented

server-side shape generation. The advantage of this

approach lies in the deferred shape generation on the

graphics board (GPU) for only items that are visible

in the current view frustum.

3.1 Preliminaries

All rendering techniques make the following assump-

tions on the structure and visualization of a 3D-

Treemap. A 3D-Treemap can be considered as a spe-

cial case of 2.5D virtual environment. Such VE is

usually not viewed from below, thus, we do not con-

sider the bottom faces of a treemap item important.

Further, for the simpliﬁcation of the geometric

representation, it is assumed that 3D-Treemap items

are aligned with world space coordinate axis. Fur-

thermore, we assume that attributes for thematic map-

pings vary usually per treemap item as well as that

thematic mappings vary more often than the layout of

a 3D-Treemap changes.

InteractiveRenderingofComplex3D-TreemapswithaComparativePerformanceEvaluation

167

Layout & Thematic Mapping. There are several

layout approaches for 2D-Treemaps (e.g., squariﬁed

(Bruls et al., 2000) or strip layouts (Bederson et al.,

2002)). For simple 3D-Treemaps the layout costs

are usually higher than the rendering costs. Since,

3D-Treemaps are basically 2D-treemaps with an ad-

ditional height value per item, existing layout ap-

proaches can be used. Thus, the layout-dependent at-

tributes of a 3D-Treemap item are 2D position (hor-

izontal and vertical) and 2D dimensions (width and

height).

However, changes in the layout caused by modi-

ﬁcation of the underlying data can be separated from

changes in the visual appearance due to altering the-

matic mappings (layout-independent attributes): both

can occur at different frequencies. Consequently, but

depending on the respective applications, one can as-

sume that separate handling of layout-depended and

layout-independent attributes has inﬂuence on the

update performance and thus, the rendering perfor-

mance.

Figure 3: Comparison of the geometric representation for a

2D (left) and a 3D- treemap item (right).

3D-Treemap Items. The additional dimension in-

troduces additional geometric complexity, i.e., geo-

metric primitives. A 3D-Treemap item requires three

to ﬁve (depending on the use of backface-culling)

times more geometry than a 2D equivalent. In con-

trast to 2D-Voronoi-Treemaps (Balzer and Deussen,

2005), classical 2D-Treemaps (Bruls et al., 2000)

have a squared footprint that can be geometrically

represents using two triangles (Fig. 3 left). Extending

the 2D-Treemap concept to the third dimension intro-

duces at minimum ﬁve times more geometric primi-

tives (Fig. 3 (right)).

For complex 3D-Treemaps an important goal is

to provide a minimal representation, with a small-

as-possible memory footprint on client. The size of

the item representation determines the update perfor-

mance. Further, memory alignment should support

fast client-server updates.

In contrast, to Voronio or cicurlar treemap ele-

ments, a standard treemap item is represented using

a 3D box. A treemap item T of a treemap T can

be expressed as: T = (P, D,C, id, F). The position

P = (x, y, z) ∈ R

represents the origin of the cube, the

extends by dimension D = (w, h, d) ∈ R

, the color

C ∈ [0, 1] ⊂ R

. In addition thereto, a treemap item

can store a number of ﬂags F, describing properties

such as the hierarchy depth or if it is a leaf node. The

unique object identiﬁer id enables the usage of indi-

rections during rendering, i.e., if attributes changes:

no geometry update is required.

Based on the previous layout assumptions, the

presented concept uses two buffers that can be up-

dated separately to save bandwidth and update time

for animated treemaps (Section 4). One buffer rep-

resents the static layout-dependent information (i.e.,

x, y, w, h) while the other one contains the information

about possibly dynamic, layout-independent proper-

ties (i.e., z, d,C).

Compact Representation The major goal is to pro-

vide a compact representation of the 3D-Treemap that

is suitable for client and server storage by conveing

high frame rates at the same time. Figure 5 shows

the used geometry template for an indexed represen-

tation for a cube without a bottom face. It only re-

quires 8 vertices and 12 indicies to describe ten faces.

To summarize, the compact representation also en-

ables a lossless compression for 3D tree maps. For

example, table 1 compares the memory footprints for

n treemap items described by the number a of 32bit

ﬂoating point attributes, with a 4Byte representation

of each one. It achieves a compression ratio of 1:2.5

over and index vertex representations and a ratio of

1:3.75 over non-index vertex representations.

This form of lossless compressed representation can

especially be applied for transferring geometric data

using the world wide web. It can become especially

suitable for client-side rendering using WebGL, if ge-

ometry shader functionality will be supported in fu-

ture speciﬁcations.

3.2 Shape Generation Approach

This fully GPU accelerated, single-pass rendering ap-

proach is based on the idea of Instance Culling or In-

stance Cloud Reduction (R

akos, 2010), which origi-

nally comprises a culling pass and a rendering pass.

We modify the concept by omitting the culling pass

and by shifting the geometric representation and the

assembly of each geometric instance completely to

the geometry shader.

Figure 4 shows an simpliﬁed overview of the ren-

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

168

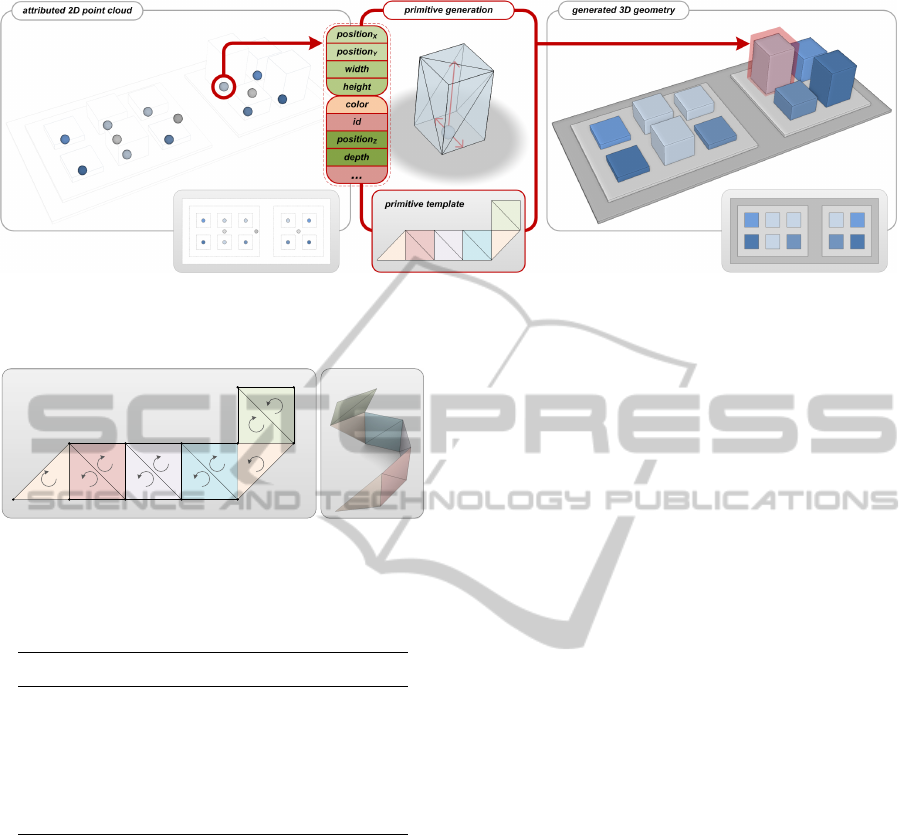
Figure 4: Simpliﬁed rendering pipeline for the shape generation approach presented in this paper. An attributed point cloud

is converted to cubes using a primitive template in the geometry shader stage. The insets shows the test datasets from a 2D

perspective.

+X -Z -X

treemap item triangle strip unrolled perspective view

Figure 5: Example of a primitive template: triangle strip for

representing a 3D-Treemap item on GPU.

Table 1: Comparing memory footprints of the rendering

techniques on VRAM in Byte.

Rendering Technique Memory Footprint

Shape Generation n · (a · 8) + 24 + 12

Indexed VBO n · (a · 8 + 12)

Non-Index VBO n · (a · 30)

Pseudo Instancing 8 + 12

UBO Instancing n · (a · 8) + 24 + 12

TBO Instancing n · (a · 8) + 24 + 12

dering pipeline for the proposed shape generation ap-

proach. Buffer objects encode all items as attributed

point cloud. The point position is the origin of the

3D-Treemap item. During a single draw call, a ge-

ometry shader converts a input point into a triangle

strip, representing the shape of the 3D-Treemap item,

using the indexed primitive template described in the

previous section.

3.3 Vertex Buffer Approaches

An alternative to the shape generation approach is the

rendering using server-side resources known as buffer

objects. Buffer objects is the general term for unfor-

matted linear memory, allocated by the graphics con-

text (Segal and Akeley, 2012). These can be used to

store vertex data. For comparison reasons, two GPU

representation variants for 3D-Treemaps are evalu-

ated:

Indexed Buffer Objects. Indexing, or indexed ver-

tex rendering, enables the reuse of vertices by

using an additional index buffer. In this way,

a treemap item can be represented using eight

vertices and 12 indices (Fig. 5). Indexed

vertex rendering also leverage the GPU’s post-

transform cache (post-T&L cache) (ca. 32 ver-

tices) that reuses already transformed vertices

(Hoppe, 1999).

Non-Indexed Buffer Objects. For reasons of com-

pleteness, we compare the shape generation ap-

proach with the non-indexed buffer object repre-

sentation. Here, a treemap item is represented us-

ing ten faces with three vertices. The represen-

tation does not utilize post-transform cache and

has the largest video memory footprint of all com-

pared rendering techniques.

In contrast to shape generation, such explicit buffer

representation exhibit higher memory consumptions

and increased update-time per treemap item, since the

shape generation is performed client side for the com-

pact treemap representation described in Section 3.1.

3.4 Geometry Instancing

Another important technique for the interactive ren-

dering of uniform geometry is geometry instancing

(Nguyen, 2007). It enables the rendering of a num-

ber of copies (instances) of a single geometric object

in a single draw call and thereby improves the poten-

tial runtime performance. This technique is primar-

ily used for objects such as trees (Bao et al., 2011),

grass, buildings, or objects which can be in general

represented as repeated geometry. Although vertex

data is duplicated across all instanced meshes, each

InteractiveRenderingofComplex3D-TreemapswithaComparativePerformanceEvaluation

169

instance can have differentiating parameters (per-

instance data). This paper evaluates three common

instancing techniques that mainly differ by the encod-

ing of per-instance data such as dimension, color, and

object identiﬁer.

Pseudo Instancing. encodes the instance data in the

shader constant registers. These registers are usu-

ally limited to 4k of ﬂoating point values. Pseudo

instancing requires most draw calls because of

the limited number of instances that can be rep-

resented.

Uniform-Buffer Instancing. stores instance data in

uniform buffer objects (UBO) (often with a max-

imum buffer size of 64k). The maximal size of

a uniform buffer determines number of instances

rendered with a single draw call, i.e., the num-

ber of draw calls required to render the complete

treemap.

Texture-Buffer Instancing. uses so called texture

buffer objects (TBO) that provide a 1D storage

as a texture. Similar, to uniform-buffer instanc-

ing, the maximum size of a texture buffer deter-

mines number of draw call. The instance data is

accessed using texel fetches during shader run-

time. The number of item attributes determines

the number of texel fetches required.

For a test machine equipped with a NVIDIA GTX

460, a 3D-Treemap data comprising 614,929 items

the per-instance data require 29,516,592 byte. Pseudo

instancing requires 1809 draw calls with 340 instance

per call, while uniform buffer instancing requires 453

draw calls with 1360 instances per call. Since buffer

textures can be substantially larger than equivalent

one-dimensional textures (up to 2

texels), texture

buffer instancing requires only a single draw call. The

performance impact of each technique is discussed

detailed in Section 5.

3.5 Culling Optimizations

The implementation of the rendering techniques de-

scribed above support the following three culling

techniques to improve rendering performance:

View-Frustum Culling. View-frustum culling per-

formed in the vertex stage is used to omit the

shape generation for treemap items outside the

current view frustum. A two-stage approach is

applied: ﬁrst; test only the origin point, if it is

out-side the current view frustum, each one of the

eight corner points are tested.

Size-Culling. If a 3D-Treemap item passes view-

frustum culling, the area of its projected shape in

viewport

treemap item

width w

item area A

width a

height h

height b

Figure 6: Parameters in screen-space coordinates required

for size culling a 3D-Treemap item.

screen space is tested. No geometry is emitted if

the size is below a threshold . This reduces raster-

ization costs.

Back-Face Culling. To further reduce rasterization

costs, back-face culling is enabled for 3D scenes

with opaque geometry.

The application of occlusion culling is not consid-

ered due to the low geometric complexity of the

3D-Treemap items, i.e., simple approximations of

treemap geometry have the same complexity, thus oc-

clusion culling wont give any beneﬁts. Further, user

mainly look from top-down or oblique perspectives,

thus, most items are visible and not overdrawn.

The size culling approach omits the rasterization

of treemap items which dimensions are too small to

be perceived on screen. This can signiﬁcantly re-

duces the load of the rasterization stage in the ren-

dering pipeline. We propose a screen-space metric in

combination with a threshold ε > 1 over the item area

A of a projected treemap item (Figure 6):

passSizeCulling(a, b, ε) =



1 a · b > ε

0 otherwise

The area A computes from the 2D hull (axis-

aligned bounding box) of the projected corner points

, . . . , p

of a 3D-Treemap item:

a = |max(p

, . . . , p

)| − |min(p

, . . . , p

b = |max(p

, . . . , p

)| − |min(p

, . . . , p

For a given viewport resolution of w width and h

height, we observed that ε ∈ [1, 2.5] the trade-off be-

tween performance improvement and visual artifacts

seems optimal.

4 IMPLEMENTATION DETAILS

To evaluate and compare the performance of the

rendering techniques described above, a prototypi-

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

170

Layout Attributes Thematic Mapping Attributes

Layout Buffer Thematic Mapping Buffer

Figure 7: The Split-buffer concept for layout and thematic

mapping information reduces update performance due to to

reduction of consumed bandwidth.

cal implementation using OpenGL (Segal and Ake-

ley, 2012) and GLSL is presented. The implemen-

tation uses modern GPU capabilities such as vertex

buffer objects (VBO), vertex array objects (VAO),

texture buffer objects (TBO), and uniform buffer ob-

jects (UBO). Assuming that the remaining techniques

are well documented, this section focus on implemen-

tation details for the shape generation approach.

Buffer Management. Based on the assumption that

changes in thematic mapping occur more often than

layout changes, we decided to use two buffer ob-

jects: one represents the 2D layout information (lay-

out buffer) and the other represents the thematic map-

ping (thematic mapping buffer) information (Fig. 7).

The buffer contents is organized in groups of four

32bit ﬂoat values to support memory alignment con-

straints of the GPU. The split buffer implementation is

only relevant for the shape generation, uniform-buffer

as well as texture buffer instancing approaches.

Shape Generation using Shader. For encoding the

primitive template, one can use the approaches sim-

ilar to encoding per-instance data (Section 3.4). We

encode the primitive template using shader constant

registers. Independent of the encoding, the size of

the primitive template (e.g., the number of primitives

represented) is effectively limited by the number of

vertices and attributes that can be emitted by the ge-

ometry shader: 4096 ﬂoat values.

The listing in Fig. 8 shows the OpenGL geome-

try shader implementation used for shape generation

stage. The geometry template is encoded using con-

stant shader registers for fast access. Shape genera-

tion is triggered only if the input point passes view-

frustum and size culling performed in the previous

vertex shader stage. The number of output vertices

of the geometry shader is capped to 12.

The ﬁrst loop scales each vertex of the template

with respect to the dimension of the 3D-Treemap

item. The scale vertex is then translated to the item

origin and than projected. The compiled (unrolled)

geometry shader requires only 120 assembly instruc-

tions for the respective geometry template.

3D-Treemap Stylization. Suitable styling of 3D-

Treemaps is essential for human perception. It

should support the differentiation between single

treemap items and facilitate the visual extraction of

the treemap hierarchy. Stylization is implemented as

a post-processing step in the rendering pipeline. Fig-

ure 9 shows an overview of the stylization stage and

participated components. The G-Buffer (Saito and

Takahashi, 1990) required for the deferred stylization

are generated using render-to-texture (RTT) (Wynn,

2002) in combination with multiple rendering targets

(MRT). The overhead in rendering performance intro-

duced by RTT varies between 1-3 milliseconds on a

NVIDIA GTX 560, depending on the screen resolu-

tion.

Figure 9 shows a comparison example for the used

stylization variants, ordered by the impact on the ren-

dering performance. Plain coloring and a single dis-

tance light (Fig. 9.A) performs best but makes it dif-

ﬁcult for a user to differentiate between the treemap

items (Bohnet and D

ollner, 2011). This can be par-

tially improved by implementing image-based edge-

enhancement (Nienhaus and D

ollner, 2003) (Fig.

9.2). For this stylization feature, per-face normal vec-

tors are required. The normal vector information is

not part of the treemap representation and generated

procedurally using a geometry shader. For a trian-

gle T = (V

) the normal N is simply computed

by N = normal(T ) = |V

− V

| × |V

− V

|. For the

shape generation approach the normal vectors are ex-

plicitly given for each emitted vertex using last pro-

voking vertex (Segal and Akeley, 2012).

5 RESULTS & DISCUSSION

This section presents a comparative performance

evaluation of the presented approach and discusses

limitations and ideas for future work.

in vec4 v4_Dimension_VS[1];

in float v1_Pass_VS[1];

const vec4 VERTEX[8] = vec4[](/* ... */);

const int INDEX[12] = int[](/* ... */);

void main(void){

if(v1_Pass_VS[0] > 0.0){ // pass view-frustum & size culling

vec4 VERTEX_TRANSFORM[8];

for(int i = 0; i < 8; i++) // Transform template vertices

VERTEX_TRANSFORM[i] = gl_ModelViewProjectionsMatrix *

(gl_PositionIn[0] + (VERTEX[i] * v4_Dimension_VS[0]));

for(int j = 0; j < 12; j++){ // Emit primitive

gl_Position = VERTEX_TRANSFORM[INDEX[j]];

EmitVertex();

}

Figure 8: GLSL geometry shader for the shape generation

approach using shader constant registers to represent the

primitive template.

InteractiveRenderingofComplex3D-TreemapswithaComparativePerformanceEvaluation

171

compositing

shading edges occlusion

final imageimage layer

depth normal identity color

Figure 9: Image-based stylization pipeline used for all presented rendering techniques. The G-Buffer for depth, normal,

identiﬁer, and color, are rendered within a single using multiple render targets. The compositing stage use this data to

synthesize various treemap stylization.

1234

Figure 10: Various stylization alternatives supported by the

stylization pipeline, without (A) and with static lighting (B).

From left to right shows the item color only (1), applied

edge-enhancement (2), unsharp masking (3), and unsharp

masking combined with edge enhancement (4).

5.1 Test Setup

The rendering technique was tested using four data

sets of different geometric complexity: 35.089,

96.658, 365.645, and 614.929 items. The perfor-

mance tests are conducted on three different test plat-

forms with different GPU generations: (1) NVIDIA

GeForce GTX 460 GPU with 1024MB video mem-

ory on an Intel Xeon W3530 CPU with 2,8GHz and

6GB of main memory; (2) NVIDIA GeForce GTX

480 with 1.5GB video memory on an Intel Xeon

W3520 2.67GHz and 24GB of main memory; and (3)

NVIDIA GeForce GTX 560 Ti with 2GB video mem-

ory on an Intel Xeon W3550 3.07GHz and 6GB of

main memory.

The test application runs in windowed mode at

high-deﬁnition resolution of 1280 × 720 pixels. The

complete scene is visible in the view frustum, thus

view-frustum culling is not applied. Further back-

face culling is activated and size culling is deacti-

vated. For each rendering technique, a total of 5000

consecutive frames are rendered and the respective

run-time performance in milliseconds is tracked. Af-

ter performance tracking, all records are averaged. To

determine to update performance, the time required

between committing a new data set to the rendering

techniques and the next frames rendered is measured

in milliseconds. Styling is turned off to measure ge-

ometry throughput only with the RTT overhead.

1999296 1555008 14235552 11072096 52652880 40952240 88548480

15439008 14994720 109930096 106766640 406597240 394896600 683791040

444288 0 3163456 0 11700640 0 19677440

CPU GPU CPU GPU CPU GPU CPU GPU

13.884 98.858 365.645 614.920

444288 444368 3163456 3163536 11700640 11700640 19677440 19677520

444368 444368 3163536 3163536 11700640 11700640 19677520 19677520

1999296 1555008 14235552 11072096 52652880 40952240 88548480 68871040

15439008 14994720 109930096 106766640 406597240 394896600 683791040 664113600

444288 0 3163456 0 11700640 0 19677440 0

100

1000

10000

100000

1000000

10000000

100000000

1E+09

byte

Figure 12: Memory footprint comparison of the presented

rendering techniques using four test datasets. The ver-

tical axis shows the amount of Bytes required for the

client-(CPU) and server-side (GPU) representation of 3D-

Treemaps using a logarithmic scale.

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

172

SG PI UI TI IV NV IM

35,089

1.68 3.11 2.29 2.3 2.12 3.85 13.42

98,858

2.25 6.58 4.53 4.53 3.88 9.48 36.52

365,645

6.77 22.94 15.78 15.68 13.24 33.15 133.08

614,920

13.51 38.1 26.04 26.04 21.98 56.15 237.59

100

1000

milliseconds

GTX 460

SG PI UI TI IV NV IM

35,089

1.23 3.12 1.96 2.01 1.38 2.21 15.37

98,858

1.02 7.48 4.07 3.91 1.81 4.74 38.78

365,645

3.11 29.55 15.93 15.23 6.25 17.24 146.78

614,920

7.7 46.68 24.21 23.42 10.79 28.61 243.89

100

1000

miliseconds

GTX 480

GPU

19677520

920

SG PI UI TI IV NV IM

35,089

1.28 2.64 1.91 1.91 1.57 3.37 12.45

98,858

1.51 7.74 3.43 4.01 2.87 8.09 33.65

365,645

4.89 23.47 13.48 13.42 9.60 28.81 131.54

614,920

10.03 42.01 22.24 22.41 16,15 48.17 212.87

100

1000

milliseconds

GTX 560

Figure 11: Comparison of the rendering performance for the presented rendering techniques on three different hardware

platforms using four test datasets of varying complexity. The vertical axis shows the run-time performance in milliseconds on

a logarithmic scale.

5.2 Performance Evaluation

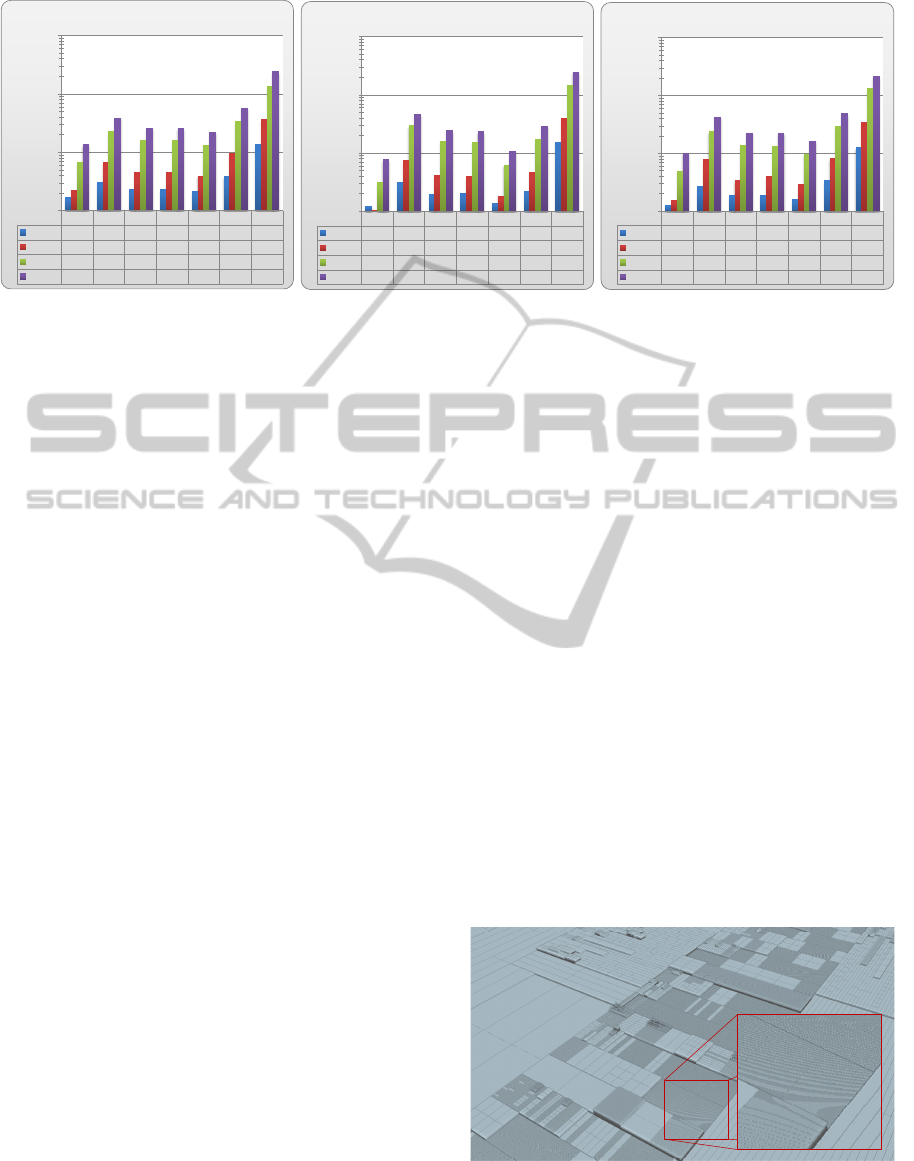
Figure 11 shows the results for the run-time per-

formance evaluation for the novel shape generation

(SG), pseudo instancing (PI), uniform-buffer instanc-

ing (UI), texture-buffer instancing (TI), index vertex

buffer (IV), non-indexed vertex buffer (NV), and in-

termediate approach (IM). Figure 12 shows the re-

spective memory consumptions important for com-

parison. The visualized values are computed based

on the functions presented in Table 1. The results

show that the presented server-side shape generation

approach outperforms the remaining rendering tech-

niques on all tested hardware platforms. Indexed

vertex- buffer rendering outperforms geometry in-

stancing but comes at the cost of a larger memory foot

print.

Uniform-buffer instancing outperforms pseudo-

and texture-buffer instancing. In comparison to

texture-buffer instancing, the number of required

draw calls are higher, but the data access (L1 for uni-

form buffers) is faster (L2 for texture buffers). The

performance of pseudo-instancing is CPU-bound be-

cause of the limited constant shader memory. The

memory footprint the server-side 3D-Treemap repre-

sentation of the instancing and shape generation are

almost the same.

Rendering in intermediate mode do not require

any video memory for the representation of a 3D-

Treemap but is CPU-bound and thus performs worst.

Non-indexed vertex buffer rendering performs worst

of all rendering techniques using server side storage.

5.3 Discussion & Future Work

To summarize, if video memory is a limiting fac-

tor, shape generation and instancing approaches are

preferable over vertex-buffer approaches. Based on

the average run-time performance, the estimated the-

oretical number of 3D-Treemap items that can be ren-

dered in real-time (assuming 12 frames-per-second)

is approximately 5 millions.

However, the presented approach and its imple-

mentation has some conceptual and technical limita-

tions. One major technical limitation concerns the

encoding of the primitive template. Its geometrical

complexity is limited to primitives and its attributes

that can be represented using 4096 ﬂoat values. (as

described in Section 4).

Figure 13 shows a rendering of a complex 3D-

Treemap. Due to static layout and border sizes,

the perspective projection introduces cluttering and

Moir

e effects. Further, single 3D-Treemap items can-

not be perceived anymore and complex 3D-Treemaps

of the presented extends are hard to read and to inter-

pret. To challenge these conceptual problems, some

aspects of the treemap layout should be altered dur-

ing rendering in a view-dependent or view adaptive

way. This requires effective level-of-detail or level-

Figure 13: Problems for rendering of complex 3D-

Treemaps: indistinguishable 3D-Treemap items (A) and

Moir

e effects (B) caused by perspective projection and high

zoom levels.

InteractiveRenderingofComplex3D-TreemapswithaComparativePerformanceEvaluation

173

Figure 14: Visualization of overdraw for a 3D-Treemap of

35k items using a slice’n dice layout. Dark areas show high

amount of overdraw (gamma-corrected).

of-abstraction approaches, which can be applied in

real-time during rendering.

Although, the rendering techniques are not ﬁll-

limited, overdraw can be a further topic to address

further performance increase (Sander et al., 2007).

The current data representation for the shape gener-

ation approach enables independent (height) scaling

of each item but exhibit a relatively large amount of

overdraw (Fig. 14). The average overdraw ratio of all

rendered fragment to all visible fragments for a data

set of 35k 3D-Treemap map items using a strip layout

and oblique viewing of (Fig. 14) orientation are 96

percent, i.e., almost every pixel is overdrawn once.

To reduce the overdraw ratio for possibly complex

fragment processing, we strive for representing the

3D-Treemap item origin and dimensions based (cur-

rently Fig. 15.A) on a function of the level within the

treemap hierarchy (Fig. 15.B).

For future work, we plan to focus on hardware

accelerated implementation of treemap layout algo-

rithms using parallel processors to enable true inter-

active 3D-Treemaps. We further strive towards a gen-

eralization of the rendering concept to support other

types of 3D-Treemaps, such as 3D Voronoi treemaps

(similar to (Choi et al., 2011)). Further, to deal for

3D tree maps with even higher geometric complexity,

we plan to combine our approach with dynamic spa-

tial data structures, such as the skip quad tree (Epp-

stein et al., 2005), and out-of-core rendering tech-

Figure 15: Side view for a possible approach to reduce un-

necessary overdraw (A) by computing the the origin and di-

mension of a 3D-Treemap item based on its hierarchy level

L (B).

niques. Furthermore, to increase the perception of

complex 3D-Treemaps we research to what extent

known level-of-detail (LoD) and level-of-abstraction

(LoA) approaches (e.g., for the visualization of vir-

tual 3D city models (Glander and D

ollner, 2007)) can

be transfered to the rendering and visualization of 3D-

Treemaps.

6 CONCLUSIONS

This paper presents a novel rendering technique that

enables real-time image synthesis of complex 3D-

Treemaps. It can be completely implemented using

consumer graphics hardware and outperforms exist-

ing rendering approaches. The presented technique

is suitable for interaction metaphors that does not re-

quire to recompute the treemap layout. Further, it en-

ables a compact, i.e., memory efﬁcient, geometry rep-

resentation of tree maps with large amount of items.

Furthermore, a throughly performance evaluation and

comparison is provided, that shows the superiority of

the presented approach over existing rendering tech-

niques.

ACKNOWLEDGMENTS

The authors would like to thank the anonymous

reviewers for their valuable comments. This

work was funded by the Federal Ministry of Ed-

ucation and Research (BMBF), Germany, within

the InnoProﬁle Transfer research group ”4DnD-

Vis” (www.4dndvis.de) and the Research School

on ”Service-Oriented Systems Engineering” of the

Hasso-Plattner-Institute.

REFERENCES

Andrews, K., Wolte, J., and Pichler, M. (1997). Informa-

tion pyramids (tm): A new approach to visualizing

large hierarchies. In Proceedings of the IEEE Visu-

alization97, pages 49–52.

Balzer, M. and Deussen, O. (2005). Voronoi treemaps.

In Information Visualization, 2005. INFOVIS 2005.

IEEE Symposium on, pages 49–56. Ieee.

Bao, G., Meng, W., Li, H., Liu, J., and Zhang, X. (2011).

Hardware instancing for real-time realistic forest ren-

dering. In SIGGRAPH Asia 2011 Sketches, SA ’11,

pages 16:1–16:2, New York, NY, USA. ACM.

Bederson, B., Shneiderman, B., and Wattenberg, M. (2002).

Ordered and quantum treemaps: Making effective use

of 2d space to display hierarchies. AcM Transactions

on Graphics (TOG), 21(4):833–854.

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

174

Bladh, T., Carr, D., and Kljun, M. (2005). The effect of

animated transitions on user navigation in 3d tree-

maps. In Information Visualisation, 2005. Proceed-

ings. Ninth International Conference on, pages 297–

305. IEEE.

Bladh, T., Carr, D., and Scholl, J. (2004). Extending tree-

maps to three dimensions: A comparative study. In

Computer Human Interaction, pages 50–59. Springer.

Bohnet, J. and D

ollner, J. (2011). Monitoring code qual-

ity and development activity by software maps. In

Proceeding of the 2nd working on Managing techni-

cal debt, pages 9–16. ACM.

Bruls, M., Huizing, K., and Van Wijk, J. (2000). Squariﬁed

treemaps. In Proceedings of the joint Eurographics

and IEEE TCVG Symposium on Visualization, pages

33–42. Citeseer.

Choi, J., Kwon, O.-h., and Lee, K. (2011). Strata treemaps.

In ACM SIGGRAPH 2011 Posters, SIGGRAPH ’11,

pages 87:1–87:1, New York, NY, USA. ACM.

Correa, W., Klosowski, J., and Silva, C. (2003). Visibility-

based prefetching for interactive out-of-core render-

ing. In Proceedings of the 2003 IEEE Symposium on

Parallel and Large-Data Visualization and Graphics,

page 2. IEEE Computer Society.

Eppstein, D., Goodrich, M. T., and Sun, J. Z. (2005). The

skip quadtree: a simple dynamic data structure for

multidimensional data. In Proceedings of the twenty-

ﬁrst annual symposium on Computational geometry,

SCG ’05, pages 296–305, New York, NY, USA. ACM.

Evans, F., Skiena, S., and Varshney, A. (1996). Optimizing

triangle strips for fast rendering. In Visualization’96.

Proceedings., pages 319–326. IEEE.

Fekete, J. and Plaisant, C. (2002). Interactive information

visualization of a million items. In Information Visu-

alization, 2002. INFOVIS 2002. IEEE Symposium on,

pages 117–124. IEEE.

Glander, T. and D

ollner, J. (2007). Cell-based generaliza-

tion of 3d building groups with outlier management.

In 15th International Symposium on Advances in Geo-

graphic Information Systems (ACM GIS). ACM Press.

Hoppe, H. (1999). Optimization of mesh locality for trans-

parent vertex caching. In Proceedings of the 26th

annual conference on Computer graphics and inter-

active techniques, SIGGRAPH ’99, pages 269–276,

New York, NY, USA. ACM Press/Addison-Wesley

Publishing Co.

Kong, N., Heer, J., and Agrawala, M. (2010). Perceptual

guidelines for creating rectangular treemaps. Visual-

ization and Computer Graphics, IEEE Transactions

on, 16(6):990–998.

Liggesmeyer, P., Heidrich, J., M

unch, J., Kalckl

osch, R.,

Barthel, H., and Zeckzer, D. (2009). Visualization of

software and systems as support mechanism for in-

tegrated software project control. Human-Computer

Interaction. New Trends, pages 846–855.

Liktor, G. and Dachsbacher, C. (2012). Decoupled deferred

shading for hardware rasterization. In Proceedings of

the ACM SIGGRAPH Symposium on Interactive 3D

Graphics and Games, I3D ’12, pages 143–150, New

York, NY, USA. ACM.

Nguyen, H. (2007). Gpu gems 3. Addison-Wesley Profes-

sional, ﬁrst edition.

Nienhaus, M. and D

ollner, J. (2003). Edge-enhancement -

an algorithm for real-time non-photorealistic render-

ing. In WSCG.

akos, D. (2010). Instance culling using geometry

shaders. http://rastergrid.com/blog/2010/02/instance-

culling-using-geometry-shaders/.

Saito, T. and Takahashi, T. (1990). Comprehensible ren-

dering of 3-d shapes. SIGGRAPH Comput. Graph.,

24(4):197–206.

Sander, P. V., Nehab, D., and Barczak, J. (2007). Fast tri-

angle reordering for vertex locality and reduced over-

draw. ACM Transactions on Graphics (Proc. SIG-

GRAPH), 26(3).

Schulz, H., Hadlak, S., and Schumann, H. (2011). The

design space of implicit hierarchy visualization: A

survey. Visualization and Computer Graphics, IEEE

Transactions on, (99):1–1.

Schulz, H., Luboschik, M., and Schumann, H. (2007). Ex-

ploration of the 3d treemap design space. Poster Com-

pendium of IEEE InfoVis07, pages 78–79.

Segal, M. and Akeley, K. (2012). The OpenGL Graphics

System: A Speciﬁcation (Version 4.2 (Core Proﬁle) -

April 27, 2012).

Shneiderman, B. (1992). Tree visualization with tree-maps:

2-d space-ﬁlling approach. ACM Transactions on

graphics (TOG), 11(1):92–99.

Sud, A., Fisher, D., and Lee, H. (2010). Fast dynamic

voronoi treemaps. In Voronoi Diagrams in Science

and Engineering (ISVD), 2010 International Sympo-

sium on, pages 85–94. IEEE.

Wettel, R. and Lanza, M. (2008). Codecity: 3d visual-

ization of large-scale software. In Companion of the

30th international conference on Software engineer-

ing, pages 921–922. ACM.

Wynn, C. (2002). OpenGL Render-to-Texture. In GDC.

NVIDIA Corporation.

InteractiveRenderingofComplex3D-TreemapswithaComparativePerformanceEvaluation

175