
A Low Cost Visual Hull based Markerless System for the Optimization of
Athletic Techniques in Outdoor Environments
A. El-Sallam
1
, M. Bennamoun
1
, F. Sohel
1
, J. Alderson
2
, A. Lyttle
2
and T. Warburton
2
1
School of Computer Science and Software Engineering, University of Western Australia, Perth, Australia
2
School of Sport Science, Exercise and Health, University of Western Australia, Perth, Australia
Keywords:
Visual Hull, Motion Analysis, Camera Calibration, Background Segmentation, Vicon, Kinetics.
Abstract:
We propose a low cost 3D markerless motion analysis system for the optimization of athletic performance
during training sessions. The system utilizes eight calibrated and synchronized High Definition (HD) cameras
in order to capture a video of an athlete from different viewpoints. An improved kernel density estimation
(KDE) based background segmentation algorithm is proposed to segment the athlete’s silhouettes from their
background in each video frame. The silhouettes are then reprojected to reconstruct the 3D visual hull (VH) of
the athlete. The center of the VH as an approximate representation of the body center of mass is then tracked
over a number of frames. A set of motion analysis parameters are finally estimated and compared to the ones
obtained by an outdoor state of the art marker-based system (Vicon). The proposed system is aimed at sports
such as javelin, pole vault, and long jump and was able to provide comparable results with the Vicon system.
1 INTRODUCTION
Motion analysis is one of the dominant and attrac-
tive fields in the area of sport biomechanics. Tradi-
tional motion analysis systems have relied on the use
of video-based techniques in the recent past mainly
in field settings and to derive kinematics. However,
with the the advent of 3D passive and active opto-
reflective systems which are regarded as the gold
standard, video-based techniques received little atten-
tion (Vicon, 2010; Roetenberg, 2006). Recent ad-
vances in Micro-Electro-Mechanical (MEMS) tech-
nology have also resulted in highly accurate and low
drift inertial sensors that attracted a large amount of
interest. 3D accelerometers have been applied in sport
analysis such as pole vault and swimming for single
or dual segment analysis, and achieved good correla-
tions with video-derived data (Callaway et al., 2009).
Opto-reflective systems have been extensively tested
in controlled indoor laboratory experiments and have
shown excellent performance compared to other sys-
tems, but have they several limitation when applied to
outdoor environments. For example, they only handle
limited field of views and require extensive setup time
and expertise for body marker placement (Roeten-
berg, 2006). Their accuracy also depends on the num-
ber of markers used (the more the markers the better
the results), similar to the idea of sampling a subject
to obtain a high resolution representation with e.g. a
3D mesh model. However, the addition of more sen-
sors can hinder the motion of the subjects (athletes). It
is not user friendly, and creates an escalating level of
complexity when orientating one sensor with respect
to another, leading to an increasing level of errors in
the outputs. Subsequently, the use of sensors alone
in motion analysis systems for example in the recon-
struction of the full body joint kinematics has been
reported to be insufficient (Roetenberg, 2006).
With the recent advancements of imaging sensors
and fast CPUs, many vision-based systems have re-
cently emerged for human action recognition. This
led Biomechanics’ researches to return to the vision
system based techniques and integrate them in motion
analysis systems. Similar to sensory based systems,
the newly developed vision based systems vary in
terms of (i) the number of cameras, (ii) camera config-
urations, (iii) the representation of the captured data,
(iv) the types of the tracking algorithms, and finally
(v) the use of subject-specific or full body models.
A survey of vision-based motion capture and analy-
sis systems is provided in (Moeslund et al., 2006).
Among the new vision system, markerless motion
analysis is currently regarded as one of the attractive
topics in sport science. Being markerless made it a es-
49
El-Sallam A., Bennamoun M., Sohel ., Alderson J., Lyttle A. and Warburton T..
A Low Cost Visual Hull based Markerless System for the Optimization of Athletic Techniques in Outdoor Environments.
DOI: 10.5220/0004291000490059
In Proceedings of the International Conference on Computer Graphics Theory and Applications and International Conference on Information
Visualization Theory and Applications (GRAPP-2013), pages 49-59
ISBN: 978-989-8565-46-4
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

pecially challenging task and one that has received lit-
tle attention due to the inherent challenges faced when
tracking an athlete’s motion in dynamic scenes.
In this work we propose a low cost markerless sys-
tem that can provide a valuable feedback to coaches
and athletes to monitor and optimize athletic tech-
niques. The system, in its current stage, can be used
in sports such as jumping, throwing, pole vault, and
javelin throw. It can also be used in other sports that
do not essentially require the tracking of the full body
joint kinematics rather require information extracted
from the tracking of the global body shape of the ath-
letes. Such information includes; the shape and its
centroid, the center of mass and its velocity, the take-
off data, and the maximum jumping height. These pa-
rameters are considered to be sufficient in the afore-
mentioned sports to provide significant feedback to
coaches and enable them to optimize athletic perfor-
mance (Bartlett, 2007).
In a typical sport training scenario, our system
uses a number of calibrated and synchronized cam-
eras to capture a video of an athlete from different
viewpoints. A background segmentation process is
then used to segment the athlete’s body from each
video frame in each camera view. The silhouettes
of the segmented body are then reprojected to recon-
struct an estimate of the 3D body shape of the athlete,
known as the visual hull (VH). The VH is then tracked
over a number of frames and a set of motion analysis
parameters are finally estimated and compared with
the ones estimated by an advanced, outdoor state of
the art and expensive marker-based system (Vicon).
Compared to gold standard systems, the developed
system is low cost compared with expensive 3D ac-
quisition systems, e.g., laser range finders or opto-
reflective systems. It does not require extensive setup
time, and is markerless. It is consequently more user
friendly,and does not require mark up expertise. Most
of the marker-based systems have a limited field of
view and their opto-reflective ones suffer from false
reflection problems known as the ghost problem. The
proposed system is tested in real training sessions and
achievedcomparable results compared to the ones ob-
tained by a Vicon system.
The paper is organized as follows; in Sec. 2 a brief
description of the overall markerless system is pro-
vided. In Sec. 3 and 4 we describe the off-line and
on-line phases of the system respectively supported
by some examples. In Sec. 5 we present the athletic
reconstruction and optimization techniques. In Sec. 6
we report and discuss our experimental results and a
conclusion is provided in Sec. 7.
2 THE OVERALL SYSTEM
The proposed system is divided into two main phases;
an off-line phase and an online phase as shown in
Fig. 1. In the off-line phase, a setup of all the cameras
of the markerless system and the vicon system is con-
figured in ordered to provide an optimal reconstruc-
tion of the athlete 3D shape and joint locations. The
cameras intrinsic and extrinsic parameters of the two
systems are then estimated and referenced to the same
world coordinates (Sec. 3.1). The markerless system
employs eight HD color cameras while the Vicon sys-
tem uses 24 opto-reflectivecameras. Finally, the opto-
reflective markers are attached to several anatomical
landmarks of the athlete’s body by an expert which
are tracked by the Vicon system and used as ground
truth. In the online phase, a trigger is used to synchro-
nize all of the markerless cameras. A background seg-
mentation algorithm is then applied (Sec. 4.1) to seg-
ment the athlete (foreground) from the background in
each video frame in all camera views. Image morph-
ing is then used to estimated the silhouettes of all the
segmented subject which are next used to reconstruct
the subject’s VH (Sec. 4.2). A set of motion analysis
parameters are then estimated from the centroid of the
VH and compared with the ones estimated by the Vi-
con system. The following section provides a detailed
description about each of the aforementioned process.
3 OFF LINE PHASE
This section presents the various processes that are
done off-line prior the sport testing sessions. It in-
cludes the camera configuration and calibration pro-
cesses, scene setup and hardware setup needed for the
data collection. The hardware includes, the marker-
based system (Vicon) which uses 24 infra-red cam-
eras, a Vicon server with fast CPUs, and over 60
markers per subject. The markerless system has eight
HD color cameras, eight fast nano-falsh recorders that
can save videos without compression, an electronic
trigger, and a circuit with LED trigger for video syn-
chronization.
3.1 Camera Configuration and
Calibration
In order to determine the 3D location of a point in
a scene, two or more calibrated cameras are needed.
However, in stereo triangulation for example, it is
well known that the position of one camera with re-
spect to the other impacts on the accuracy of the deter-
mined 3D location using their 2D projections. Tradi-
GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications
50

Figure 1: A block diagram which summarizes the overall system model.
tion camera calibration is done using a known calibra-
tion pattern or a cube. The most well known method
is the chess board based one which was developed by
Bouquet in (Bouguet, 2010). This method provides
accurate calibration results, however it is time con-
suming and not applicable to large scale outdoor envi-
ronments (where large chess board patterns would be
required). In this work we considered three different
phases in order to (i) achieve an optimal camera con-
figuration which is restricted by the size of the testing
area and to (ii) estimate accurate camera calibration
parameters for the considered large field of view. The
three phases depend on each other and are very essen-
tial for the estimation of an accurate 3D location of a
point in the scene.
3.1.1 Phase 1: Camera Configuration
In this phase, we configure a multi-view system uti-
lizing eight HD RGB cameras and globally opti-
mize their locations to cover a testing area of around
(5 ×8)m
2
. The global optimization is done using a
cube of size (2 ×2 ×2)m
3
. The location, pose and
zooming parameters of each camera are adjusted such
that the cube can be fully seen by all cameras when
placed in each corner of the considered testing area.
This configuration will be fine tuned once the camera
intrinsic and extrinsic parameters are estimated in the
following phases.
3.1.2 Phase 2: Estimation of Intrinsic
Parameters
As mentioned earlier, in large scale testing fields, it
is not convenient to use a large chessboard to cali-
brate the cameras. This process will be time con-
suming, impractical, and inaccurate. It requires the
chessboard to occupy a significant portion of the im-
ages captured by one of the cameras while at the same
time being seen by at least another camera in order to
e.g. use stereo calibration and refer all cameras to the
same origin. On the other hand, the use of a chess-
board for calibration is known to be accurate in small
fields. As a result, in this work we used a smaller
chessboard for the estimation of the intrinsic param-
eters only, we then used an automatic method for the
estimation of the extrinsic parameters. In order to do
that and estimate the intrinsic parameters, a video of a
moving chessboard with different pose, location and
orientation is captured by each camera independently.
During this process we attempted to make sure the
squares of the board nearly covered the entire image.
Depending on the type and the quality of each cam-
era, ten to 16 frames of each video were found to be
sufficient for the estimation of the intrinsic parame-
ters. The toolbox of (Bouguet, 2010) is then applied
for the estimation of the intrinsic parameters.
3.1.3 Phase 3: Estimation of Extrinsic
Parameters
In (Svoboda et al., 2005) a multiple camera self cali-
bration algorithm is proposed. It attempts to calibrate
several cameras at once using the 2D coordinates of a
number of corresponding points in the capture images
by all cameras. Consider m cameras and n 3D scene
points S
j
= (X
j
,Y
j
,Z
j
)
T
, j = 1,2,...,n are projected
to the 2D image point u
i
j
= (u
i
j
,v
i
j
), the pixel coordi-
nates of camera i as shown in Fig. 2. Using a pinhole
model of the camera (Hartley and Zisserman, 2004),
S
j
and u
i
j
are related by,
P
i
S
j
1
= λ
i
j
u
i
j
v
i
j
1
(1)
ALowCostVisualHullbasedMarkerlessSystemfortheOptimizationofAthleticTechniquesinOutdoorEnvironments
51

Figure 2: Point-based automatic camera calibration.
where P
i
= µ
i
K
i
R
i
t
i
of size (3×4) matrix, is the
i
th
camera projection matrix whose entries are the ex-
trinsic parameters that need to be estimated. µ
i
and λ
i
j
are two unknown nonzero constants, K
i
is a (3×3)
matrix whose entries are the camera intrinsic parame-
ters, R
i
and t
i
are the rotation and translation matrices
of size (3×3) and (3 ×1) respectively. In order to
estimate P
i
,i = 1,...,m, all camera models are con-
catenated into one matrix (since S
j
is a common point
seen by all cameras), i.e.
P
1
.
.
.
P
m
"
S
1
... S
n
1
#
=
λ
i
j
u
1
1
v
1
j
1
... λ
i
j
u
1
n
v
1
n
1
.
.
.
.
.
.
.
.
.
λ
i
j
u
m
1
v
m
j
1
... λ
i
j
u
m
n
v
m
n
1
(2)
In other words, one can represent the calibration prob-
lem use the global model,
PS = W (3)
where the matrix W refers to the information belong-
ing to the image points in all cameras. The solution to
the above equation was obtained by using a process
called Euclidean stratification (Hartley and Zisser-
man, 2004). It can provide the extrinsic parameters,
followed by a factorization of P
i
,i = 1,... ,m which
can then be used for the estimation of the intrinsic
parameters. This process attempts to find a nonlin-
ear, nonsingular full rank matrix H of size (4 ×4)
such that PS = PHH
−1
S and PH and H
−1
S are Eu-
clidean (Hartley and Zisserman, 2004). Their algo-
rithm has shown to give good results, however the
image points can only be collected in controlled dark
scenes using a laser/LED pointer. It also imposes cer-
tain geometrical constraints, assumes that some inter-
nal parameters of the cameras are identical and have
known aspect ratios, which is generally less robust
and may occasionally fail in the case of somehow un-
balanced input data (Svoboda et al., 2005). These
assumptions can lead to multiple solutions for the
same camera configuration given different initializa-
tions and in some cases the estimation becomes an
ill-posed problem and provide NaN values. In our
case and since our tests are normally carried out out-
doors, the use of a laser pointer and the need of a
dark scene is not practical. In addition it has been re-
ported in (Svoboda et al., 2005) that the calibration of
eight cameras requires the above aforementioned as-
sumptions plus an orthogonality assumption. It also
requires that all principal points are known, and that
the internal camera (unknown) parameters to be the
same for all cameras (at least for initialization). This
is not valid in our case or in general since a system
may use different cameras. As a result, we first es-
timate the cameras’ intrinsic parameters in Phase 2.
We then impose these correct values/constraints into
the Euclidean stratification process described in (Svo-
boda et al., 2005).
3.2 Calibration Results
In order to acquire the image points needed for cali-
bration, we tracked a wand with one or more tennis
balls of different colors from the background. The
balls are first segmented from the background. An
algorithm is then used to best fit a circle to the the
contour of the ball, then the center of the circle is
used as the image point. Fig. 3 illustrates the process
and a video is provided in the supplementary mate-
rials. The results of the camera calibration module
Figure 3: Tracking of the ball to determine the image points
needed for the calibration process.
with respect to the same world coordinate as the Vi-
con opto-reflective system are shown in Fig. 4. On
the other hand, the Vicon system has its own calibra-
tion wand and an expensive CPU server which auto-
matically estimates the calibration parameters of the
opto-reflective cameras and provide a guide about the
location of each of them. As mentioned earlier the
Vicon system normally uses many cameras and sen-
sors to compensate for occluded or noisy markers and
it has a smaller field of view (as their opto-reflective
based cameras has no zooming function compared to
the markerless system which uses vision cameras). If
GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications
52
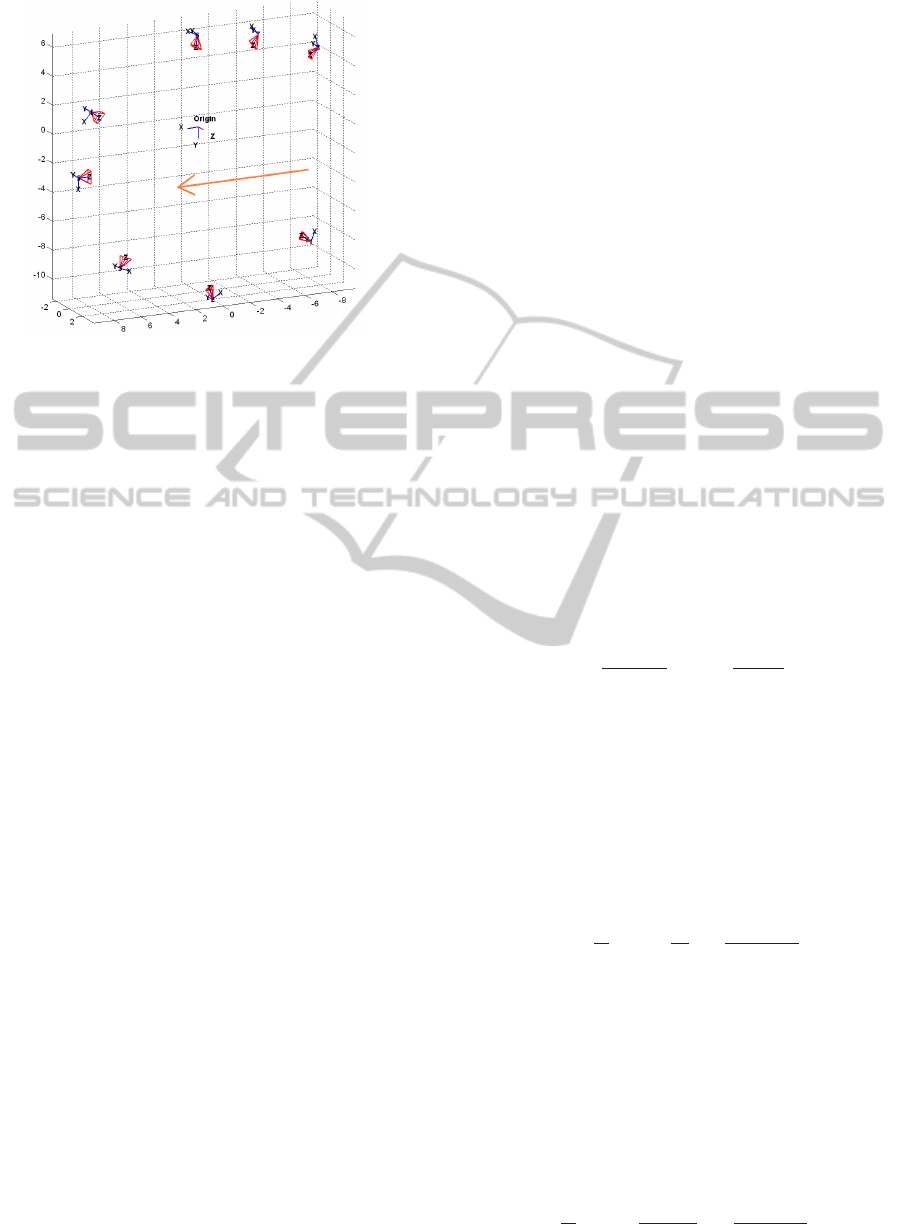
Figure 4: The final camera setup after calibration.
the Vicon cameras are placed far a apart to cover a
large field of view , a problem known as the ghost im-
age will be captured instead of the markers especially
when the light conditions vary frequently which re-
quires the system to be recalibrated.
4 ON-LINE PHASE
In this phase the system captures real-time multi-view
synchronized videos of the athlete while performing
an action. In order to minimize the 1/2 frame error
which is common in video synchronization, we used
an electronic triggering system and a LED as addi-
tional low cost option. A background, foreground
segmentation algorithm is then applied to segment the
foreground (athletes) and provides their silhouettes in
each video frame. The silhouettes of the eight views
are then reprojected to reconstruct the VH of each
frame. Finally, the center of the VH surfaces esti-
mated and tracked whereby the motion parameters are
found and compared with the ones obtained by the
marker system (Vicon).
4.1 Background Segmentation
Background Segmentations (BGs) is an important and
critical task in many computer vision applications.
There are many BGs algorithms in literature. Some
are developed to work with static scenes and oth-
ers to work with dynamic ones or both. Compar-
ative studies and surveys examined a wide-range of
BGS methods (Piccardi, 2004; Benezeth et al., 2008;
Radke et al., 2005). In the case of outdoor testing,
we face several dynamic variations including illumi-
nation changes, clouds, shadows, camera oscillations,
low and high-frequencies backgrounds (e.g. moving
subjects, tree branches). As a result, a multi modality
BGs algorithm that is capable of detecting slow to fast
background variations is required. Model-based ap-
proaches involving kernel density estimation (KDE)
functions are proven to effectively handle scenes with
varying backgrounds and are widely used in dynamic
background modeling. In this section we propose an
improved KDE-based BGS algorithm which uses a
compact weighted sum of Gaussian kernels. Gaussian
kernels are popular since they represent a generaliza-
tion of the GMM, but each single sample in this case
is considered to be a Gaussian distribution (Wand and
Jones, 1995). The improved algorithm will need to
capture and reflect past and recent information about
the background image sequence and update its model
parameters automatically and continuously.
First let us assume the samples or features
{p
1
,p
2
,...,p
N
} taken from a one distribution experi-
ment at time t. Our features in this work are the pixel
chromaticity components and their coordinates p =
(r,g,s) where r = R/(R+G+ B), g = G/(R+ G+ B),
and s = (R + G + B)/3, and R,G, and B are the
pixel’s RGB color components. We use the normal-
ized (r, g,s) color space due to its robustness to illu-
mination changes and shadows over the RGB space.
An estimate of the probability density function (pd f)
of the 3-variate pixel p at time t can be estimated us-
ing the kernel estimator,
f(p) =
1
N|H|
1/2
N
∑
n=1
K
p−p
n
H
1/2
(4)
where, K(u) is the kernel estimator function, and H
is a (3 × 3) symmetric positive definite bandwidth
(BW) matrix. A dynamic model is the one which
allows for the density function to be updated auto-
matically and follows any recent changes in the back-
ground, i.e. becomes less biased (Elgammal et al.,
2002). If one assumes that the color space compo-
nents are independent (Sheikh and Shah, 2005) then
the pdf of a pixel p at any instant t becomes
ˆ
f(p
t
) =
1
N
N
∑
n=1
3
∏
j=1
1
h
j
K
p
t
j
− p
n
j
h
j
(5)
where, p
t
= (p
t
1
, p
t
2
, p
t
3
, p
t
1
= r
t
, p
t
2
= g
t
, p
t
3
= s
t
and h
j
= H( j, j), j = 1 : 3 is a fixed BW estimator.
Several models consider the BW function to vary
with the observed pixels and the shape of the under-
lying density, i.e. adaptive. The first of these models
are called the balloon estimator. All kernels of that
model vary at each estimation point, are of the same
size and orientation and they are centered at each data
point (Sain, 2002), i.e.
ˆ
f(p
t
) =
1
N
N
∑
n=1
3
∏
j=1
1
h
j
(p
t
j
)
K
p
t
j
− p
n
j
h
j
(p
t
j
)
!
(6)
ALowCostVisualHullbasedMarkerlessSystemfortheOptimizationofAthleticTechniquesinOutdoorEnvironments
53

The other type of models is called sample-point es-
timators where a kernel is placed at each point and
with its own size and orientation regardless of where
the density to be estimated is,
ˆ
f(p
t
) =
1
N
N
∑
n=1
3
∏
j=1
1
h
j
(p
n
j
)
K
p
t
j
− p
n
j
h
j
(p
n
j
)
!
(7)
A newly observed pixel p at time t can be classified
as a foreground if the pdf
ˆ
f(p) is less than a certain
threshold T given the kernel BW h
j
and the number
of samples N. Usually, the threshold T is a global
threshold for all observed pixels/image that can be ad-
justed to achieve a desired level of false positives (El-
gammal et al., 2002). Since N can be controlled, the
estimation of the kernel BW h
j
has been the most re-
searched and critical part in this model (since it con-
trols the model accuracy). Theoretically, the opti-
mal estimates of h
j
should minimize the mean inte-
gral squared error (MISE) between the
ˆ
f(p) and the
true density f(p) (Turlach, 1993). The Rule of thumb
optimal solution assumes a reference distribution for
f(p), normally Gaussian, which asymptotically leads
to the optimal BW,
ˆ
h
j
= 1.06
ˆ
σ
j
N
−
1
5
(8)
where,
ˆ
σ
j
is the sample variance. Another approx-
imation is to assume that the local-in-time distribu-
tion is Gaussian, then the distribution for the devi-
ation (p
j
n
− p
j
n+1
) ∼ N(0,2h
2
j
) is also a symmet-
ric Gaussian. In this case the median m
j
of the
absolute deviations is equivalent to the quarter per-
centile of the deviation distribution, i.e. the probabil-
ity f
N(0,2h
2
j
) > m
j
= 0.25, leading to a BW
ˆ
h
j
=
m
j
0.68
√
2
(9)
As mentioned earlier, the BWs in Eqn. (8) and
Eqn. (9) are optimal under the asymptotical assump-
tion. They can therefore introduce a bias if the sam-
ple length is short or the BW is fixed. In this work
we consider an adaptive algorithm for the estimation
of the kernel BW. Our algorithm can use either of the
two Rule of thumb estimators in Eqn. (8) and Eqn. (9)
to build the background model, (which still require an
estimate of the sample variance). We use an adaptive,
fast and accurate estimator known as a running mean
and variance to track the variations of a pixel inten-
sity over time and reflect that in the KDE based back-
ground model. For simplicity let us omit the subscript
j and assume that the sample mean and variance at a
certain instant are µ
1
= µ, σ
1
2
= σ
2
. Then, when a
new observation arrives at a sample number t ∈Z, the
method computes the mean and variance adaptively
and adjusts the kernel BW using the recursivemethod,
ˆµ
t
=
ˆµ
t−1
+ (p
t
− ˆµ
t−1
)/t if p
t
∈ BG
ˆµ
t−1
if p
t
∈ FG
(10)
ˆ
σ
2
t
=
ˆ
σ
2
t−1
+ (p
t
− ˆµ
t−1
)(p
t
− ˆµ
t
) if p
t
∈ BG
ˆ
σ
2
t−1
if p
t
∈ FG
(11)
ˆ
h
t
= 1.06
ˆ
σ
t
N
−
1
5
, or
ˆ
h
t
=
ˆµ
t
0.68
√
2
(12)
Where BG means background and FG means fore-
ground. For Gaussian distributions the median equals
the mean value, i.e. m
t
= µ
t
. Using the above analysis,
the full background segmentation algorithm runs as
follows. Assume we have collected an offline N + M
sample images of the scene per camera. The N sam-
ple images are for the background and the M are for
a randomly moving subject in the scene. The N sam-
ples are used to build the KDE modeling and the M
samples will be used for validation and for the selec-
tion of an appropriate threshold T mentioned earlier.
T is selected such that our foreground detection rate
will achieve a desired percentage of false positives.
—————————————
Step 1: Use off-line N images of the background to estimate the sample
mean µ
N
j
and the sample variance σ
2
N
j
for each feature p
j
, j = 1 : 5 then
calculate their kernel BWs using Eqn. (8).
Step 2: Use the M validation images to select/adjust an appropriate global
threshold T for foreground detection, if
ˆ
f(p) < T then the pixel p must be
from the foreground, otherwise it is from the background.
Step 3: Initialize the running means and the running variances with the sam-
ple means and sample variances obtained in Step 1.
Step 4: When a new observation image is captured, apply the KDE model
and classify the FG and the BG pixels. If a pixel is classified as a BG esti-
mate the running means and running variances, then update the kernel BWs
following the adaptive procedure Eqn. (8) and Eqn. (9), and increase N by 1.
The learned N can also be used for prior testing to minimize false positive
detections.
Step 5: Repeat step 4 until the last frame of the observation.
—————————————
It should be noted that the accuracy of the model
increases over time (asymptotical assumption) since
the number of samples learned by the model also in-
creases. A BGS example for a javelin throw using the
proposed algorithm is shown in Fig. 5 (and a video
can be seen in the supplementary materials).
4.2 Visual Hull Reconstruction
The visual hull is a 3D geometric shape (surface) rep-
resentation of an object created using a shape-from-
silhouette reconstruction technique. It is the maximal
shape that gives the same silhouette as the actual ob-
ject for all views outside the convex hull of the object.
GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications
54

Figure 5: A KDE-based BG segmentation results in one of
our outdoors testing trials (Javelin).
This technique assumes that the foreground object or
the foreground mask (silhouette) which can be sepa-
rated from its background, is the 2D projection of the
corresponding 3D foreground object. Along with the
camera viewing parameters, the silhouette defines a
back-projected generalized cone that contains the ac-
tual object. Two or more of these silhouette cones can
be produced from the silhouette images taken from
different viewpoints. The intersection of these cones
produces a bounding geometry called a visual hull or
inferred visual hull. Although the VH is only an ap-
proximation and overestimates the true shape of the
object, it is guaranteed to enclose the object but its
size decreases monotonically with the number of im-
ages used (Laurentini, 2003). However, even when an
infinite number of images are used, not all concavities
can be modeled with a visual hull.
In this work we reconstruct the VH using silhou-
ettes of the athlete body which is segmented from the
synchronized video frames of eight calibrated cam-
eras with unsymmetrical intrinsic parameters. An ex-
ample to demonstrate the camera setup and a recon-
structed VH using the eight camera setup for an out-
door system can be seen in Fig. ??. Note that in
sports such as javelin or pole vault, the required field
of view for a complete testing trial is large . As a re-
sult, the system cameras were placed far apart from
each others to allow for the entire field of view to be
covered. The calibration of a large field of view is
a challenging task due to the vibrations of the setup
resulting from winds and the variations in light (espe-
cially when some cameras are fully or partially facing
the sun). As seen in the figure, the reconstructed VH
is representative but over/under estimates the shape
of the body due to the large field of view. However
this did not significantly impact on our results since
the sports we are considering only need the global 3D
shape of the athlete’s body.
5 ATHLETIC TECHNIQUES
RECONSTRUCTION
Our main aim is to estimate a number of motion para-
Figure 6: A large size field of view of size (4×8×2 m
3
) of
an outdoor camera setup with a top view of the VH.
rameters such as the location of the center of mass
and its velocity over time, or the maximum height of
a jump. Tracking these parameters over a number of
frames is considered effective in providing significant
kinetic feedback to the coaches to optimize athletes
performance. In this work, we investigate the use of
the center of the body shape to approximate the cen-
ter of mass. In order to do that, a female elite athlete
performed five different javelin throws. A visual hull
system using eight cameras was proposed to recon-
struct the VH to approximate the athlete body shape
in each frame in each trial. The VH centroid is tracked
over a number of frames then its coordinates and re-
sultant velocity is estimated and compare with a gold
standard system, the Vicon system. The sample fre-
quency of the proposed markerless system was 50Hz
(50 interlaced fps) where the Vicon system was per-
formed at 250Hz. For the Vicon on a residual anal-
ysis, a dual pass Butterworth filter was used but no
filtering of the markerless data was performed except
for the interpolation from 50Hz to 250Hz. Since the
results of other trails had similar results, we opted to
discuss only one of the the trials and show the chal-
lenges and propose future work. The 3D center of
the visual hull was compared to the calculated cen-
ter of mass (com) from the Vicon analysis. It should
be noted that the results of the markerless system in
this trial were the outputs of the direct analysis result-
ing from the automatic reconstruction of the VH from
the segmented foreground. No further post-analysis
refinement of the data was performed.
6 EXPERIMENTS AND RESULTS
In this section, we discuss experiments to investigate
our proposed markerless system. We also compare
its performance with a state of the art outdoor marker
based system (Vicon). In particular we aim to decide
on whether our developed markerless system can be
used as a stand-alone system for the 3D reconstruc-
tion and the optimization of the performance of the
athletes. In this example the center of the VH is used
as an approximation of the body com to track and
ALowCostVisualHullbasedMarkerlessSystemfortheOptimizationofAthleticTechniquesinOutdoorEnvironments
55

Figure 7: The ares of interest lies between frame (b) strike, and (d) release. The speed prior frame (a) and after frame (c) are
also needed for kinetic analysis. (Figure best seen in color).
Figure 8: The 3D coordinates in m of the of the center of the VH over the designated field of view wrt the markerless
coordinate system.
compare against the actual com estimated using the
Vicon system. The results of this test are shown in
Fig. 8, 9, 10 and 11 for the 3D coordinates of the
center of the Visual hull (x, y and z displacement), and
its resultant velocity respectively. From the figures, it
can be seen that the VH results across the three di-
rections especially the x-direction and z-direction are
comparable to the ones obtained by the marker-based
Vicon system. In practice the y-direction data is not
particulary useful but is shown here for completeness.
The maximum absolute error within the area of inter-
est was around 8cm which is about 0.08/4.05% er-
ror in the overall field length of 4.05m. The resultant
velocity shown in Fig. 12 which is more important
than the raw displacements (x,y,z) of our system fol-
lows (on-average) a similar behavior of the velocity
obtained by Vicon system with an absolute error of
around 1.26 m/s. It should be noted that the com-
pared results were performed in a very short duration
of 0.35 seconds (fast elite athlete) which is nearly 20
interlaced frames for the markerless system (i.e. 10
frames), and about 90 frames for the Vicon system.
GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications
56
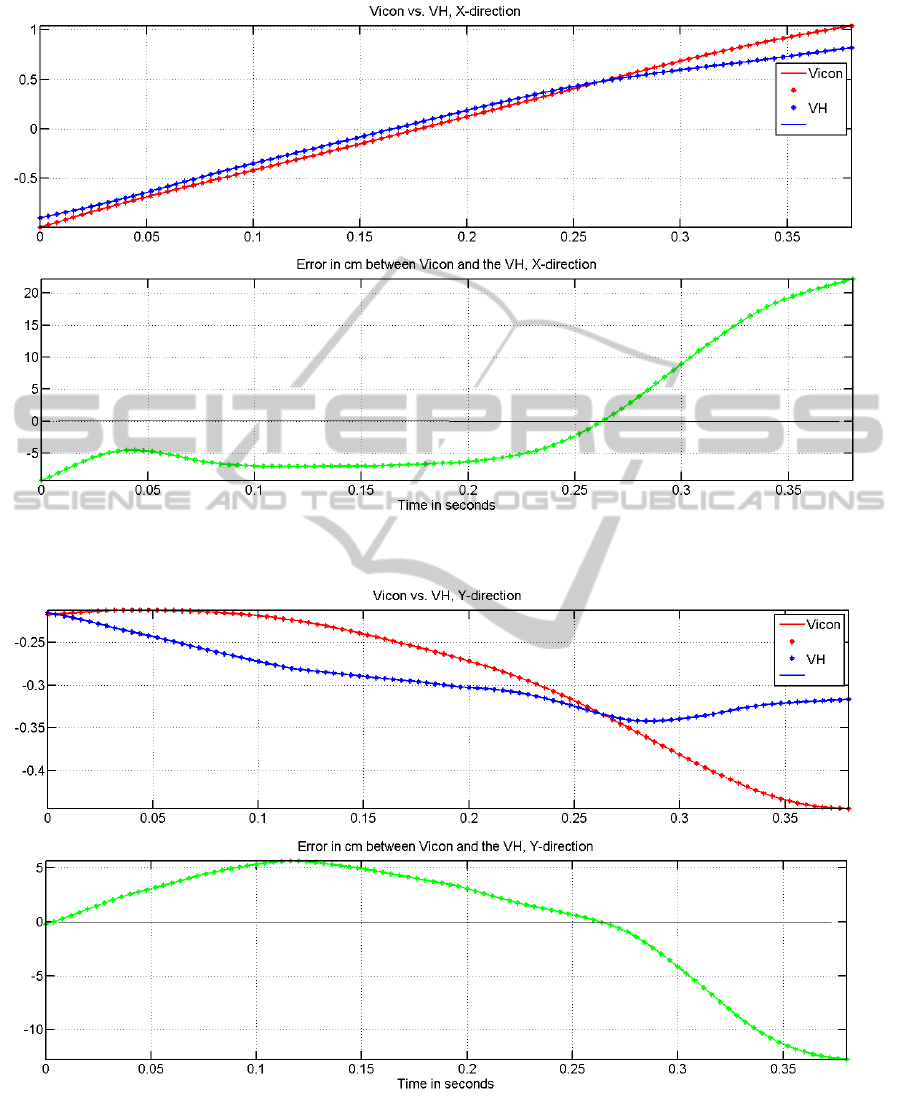
Figure 9: The horizontal displacement in m and the error in cm of the center of mass for the Vicon (red) vs the centroid of the
markerless (blue), error (green). (Figure best seen in color).
Figure 10: The width in m and the error in cm of the center of mass for the Vicon (red) vs the centroid of the markerless
(blue), error (green). (Figure best seen in color).
This short duration was a requirement of the coaches
which starts at approximately the back foot strike and
ends at the release of the arrow (javelin) (as shown in
Fig. 7). This short duration makes the tracking a dif-
ficult and a challenging task. However the results of
the markerless system were still adequate and shown
ALowCostVisualHullbasedMarkerlessSystemfortheOptimizationofAthleticTechniquesinOutdoorEnvironments
57
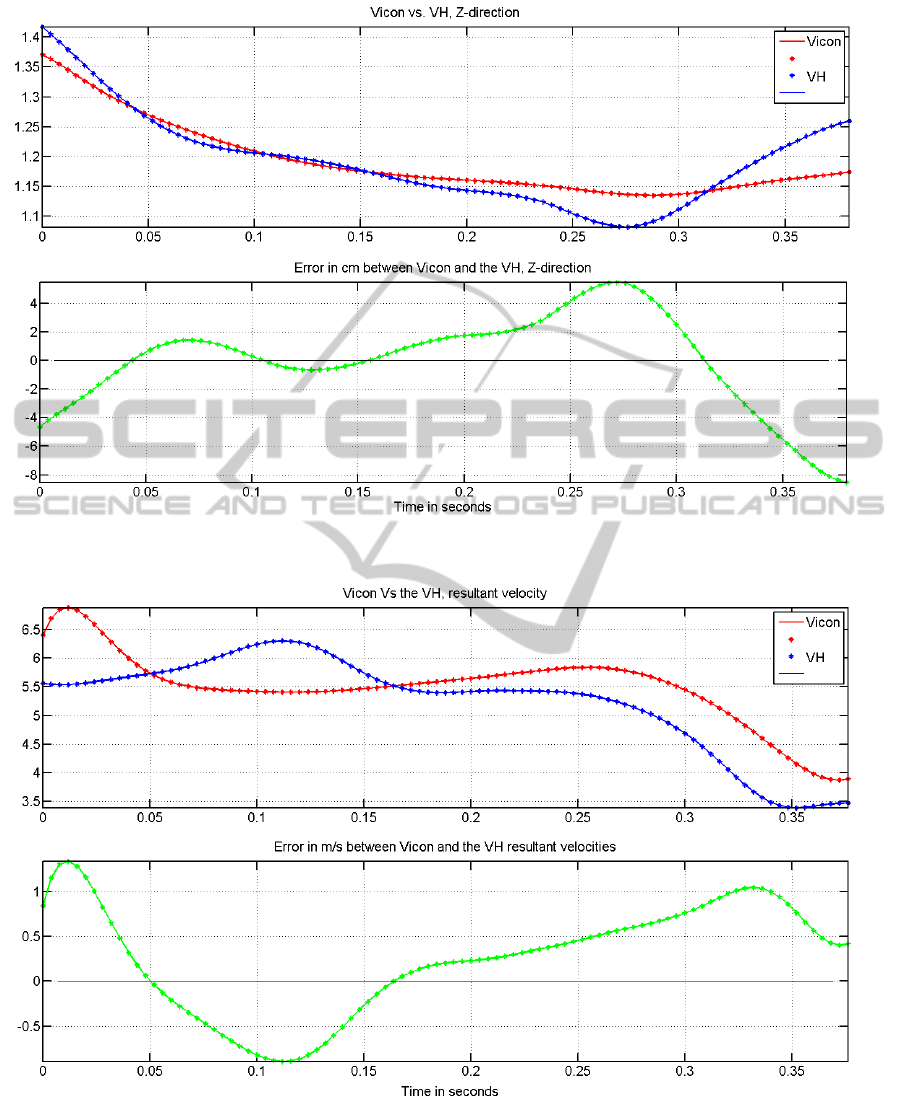
Figure 11: The height in m and the error in cm of the center of mass for Vicon (red) vs the centroid markerless (blue), error
(green). (Figure best seen in color).
Figure 12: The resultant velocity in m/s of the center of mass for Vicon (red) vs the centroid markerless (blue), error (green).
(Figure best seen in color).
a promising results that can be improved. The vari-
able errors seen at the end of the curves were due to
the non stationary background caused by moving peo-
ple and trees. In addition the results of the markerless
system include the weight of the javelin arrow itself
which was varying across the examined frames due to
GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications
58

its smaller dimension. Our future work includes giv-
ing the javelin a different color so that it can be easily
segmented and excluded the VH. We also aim to cor-
rect for the over/under estimated parts of the VH by
developing another adaptive KDE model for the fore-
ground in non stationary backgrounds and enhance
the proposed BGs model algorithm. Furthermore, to
achieve an accurate estimate and accurate tracking of
the center of mass using the vision alone, we aim in
our future work to align a scan of the body mass in-
formation known as DEXA (M. Rossi, 2012) with the
3D shape (mesh) of the athlete and use that to cal-
culate and use the shape with its registered mass to
determine more accurate center of mass. We will also
estimate the kinetics of the body and its different seg-
ments.
7 CONCLUSIONS
A low cost markerless system for the optimization of
athletes’ performance is proposed for outdoor envi-
ronments. The system utilizes multiple cameras to
capture the motion of an athlete from different view-
points and reconstruct their VH over a number of
frames. The center of the VH is used as an ap-
proximation of the center of the body mass, and es-
timated at each frame. A number of motion anal-
ysis parameters are finally calculated from the cen-
ter and compared with the ones obtained by an ad-
vanced and high cost marker-based system. Using
only eight cameras working at 25 frame per second
(de-interlaced) and no markers, the proposed marker-
less system achieved promising results compared to
the Vicon system which uses 24 opto-reflective cam-
eras and over 60 markers at 250fps (i.e. ten times
the frame rate of the markerless system). In addition
it is a user friendly and efficient system with respect
to setup and analysis time. Future work will be con-
sidered to improve the performance of the markerless
system, use body mass scans and full body joint kine-
matics to correct for the reported errors and provide
additional kinetic parameters for an improved analy-
sis.
REFERENCES
Bartlett, R. (2007). Introduction to sports biomechanics:
Analysing human movement patterns. Psychology
Press.
Benezeth, Y., Jodoin, P., Emile, B., Laurent, H., and
Rosenberger, C. (2008). Review and evaluation of
commonly-implemented background subtraction al-
gorithms. In Proc. 19th IEEE ICPR conf., pages 1–4.
Bouguet, J. (2010). Camera calibration toolbox for matlab,
2006. URL http://www.vision. caltech.edu/bouguetj.
Callaway, A., Cobb, J., and Jones, I. (2009). A compari-
son of video and accelerometer based approaches ap-
plied to performance monitoring in swimming. In-
ternational Journal of Sports Science and Coaching,
4(1):139–153.
Elgammal, A., Duraiswami, R., Harwood, D., and Davis,
L. (2002). Background and foreground modeling us-
ing nonparametric kernel density estimation for visual
surveillance. Proc. of the IEEE, 90(7):1151–1163.
Hartley, R. I. and Zisserman, A. (2004). Multiple View Ge-
ometry in Computer Vision. Cambridge University
Press, ISBN: 0521540518, 2nd edition.
Laurentini, A. (2003). The visual hull for understanding
shapes from contours: a survey. In Proc. 7th IEEE
ISSPA Conf., volume 1, pages 25–28.
M. Rossi, e. a. (2012). A novel approach to calculate body
segments inertial parameters from dxa and 3d scan-
ners data. 4th International Conference on Computa-
tional Methods (ICCM2012).
Moeslund, T., Hilton, A., and Kr¨uger, V. (2006). A sur-
vey of advances in vision-based human motion cap-
ture and analysis. Comp. vision and image under-
standing, 104(2):90–126.
Piccardi, M. (2004). Background subtraction techniques:
a review. In Proc. EEE SMC Conf., 2004, volume 4,
pages 3099–3104.
Radke, R., Andra, S., Al-Kofahi, O., and Roysam, B.
(2005). Image change detection algorithms: a system-
atic survey. IEEE Transactions on Image Processing,
14(3):294–307.
Roetenberg, D. (2006). Inertial and magnetic sensing of
human motion. PhD thesis.
Sain, S. (2002). Multivariate locally adaptive density es-
timation. Computational statistics & data analysis,
39(2):165–186.
Sheikh, Y. and Shah, M. (2005). Bayesian modeling of
dynamic scenes for object detection. IEEE PAMI,
27(11):1778–1792.
Svoboda, T., Martinec, D., and Pajdla, T. (2005). A con-
venient multicamera self-calibration for virtual en-
vironments. Presence: Teleoper. Virtual Environ.,
14(4):407–422.
Turlach, B. (1993). Bandwidth selection in kernel den-
sity estimation: A review. Institut f¨ur Statistik
und
¨
Okonometrie, Humboldt-Universit¨at zu Berlin,
19(4):1–33.
Vicon (2010). http://www.vicon.com.
Wand, M. and Jones, M. (1995). Kernel smoothing, volume
60 of monographs on statistics and applied probabil-
ity. Chapman Hall, New York.
ALowCostVisualHullbasedMarkerlessSystemfortheOptimizationofAthleticTechniquesinOutdoorEnvironments
59
