
A 2D Matching Method for Reconstruction of 3D Proximal Femur
using X-ray Images
Sonia Akkoul
1
, Adel Hafiane
2
, Rémy Leconge
1
, Eric Lespessailles
3
and Rachid Jennane
1
1
Laboratoire PRISME, Université d'Orléans, 12 rue de Blois, 45067 Orléans cedex 2, France
2
Laboratoire PRISME, ENSI de Bourges, 88 avenue Lahitolle, 18020 Bourges cedex, France
3
Institut 3MTO, Hôpital d'Orléans, 1 rue Porte Madeleine, 45032 Orléans cedex 1, France
Keywords: 3D Reconstruction, Low Dose X-ray Radiograph, Proximal Femur, Matching.
Abstract: The femur shape reconstruction from a limited number of 2D X-ray images is a challenging task but it is
desired as it lowers both the acquisition costs and the radiation dose. The aim of this paper is to use a small
number of 2D X-ray images to reconstruct a 3D proximal femur surface without any prior acknowledge of
the shape model. The proposed method combines a 2D binary contour points coordinates and their normals
to find the best matching between 2D point pairs. The obtained results are promising. The estimated error
shows that it is possible to rebuild the proximal femur shape from a limited number of radiographs.
1 INTRODUCTION
Three dimensional patient bone models play an
important role in pre-operative surgery planning and
improved guidance during surgery, modeling and
simulation. The pre-operative reconstruction of 3D
anatomical models can be achieved using the direct
3D imaging modalities such as Computed
Tomography (CT) (Gamage et al., 2011). However,
the use of such imaging is restricted to a minor
specific procedures; due to constraints placed by
cost, availability and radiation risk. Thus, the
diagnostics and planning of many interventions still
rely on two dimensional (2D) radiographic images,
where the surgeon has to mentally visualize the 3D
anatomy of interest. A direct 3D imaging must be
developed, as an alternative to current pure 2D
radiographs, in order to assist the clinicians on their
medical tasks (Gamage et al., 2011).
Literature on pre-operative reconstruction of
proximal femur based on information collected
through 2D imaging modalities can be divided into
two subgroups. The first group methodology is
based on 2D images and can be considered as
Silhouette Intersection for 3D model reconstruction
(Caponetti and Fanelli, 1993). The second group
contains methods based on a prior knowledge of the
anatomical structure as well as 2D images (Gamage
et al., 2011).
A majority of studies require prior knowledge of the
3D anatomy model to guide the reconstruction
process and to compensate the lack of information in
2D imaging modalities (Gamage et al., 2011). This
information can be provided by the integration of
one generic geometrical surface of the considered
bone structure (Laporte et al., 2003; Le Bras et al.,
2004), or by Statistical Shape Models (SSM) (Baka
et al., 2011; Zheng et al., 2009; Whitmarsh et al.,
2011).
Our aim is to study the accuracy of the 3D femur
reconstruction without using any 3D prior
information. Only, the mathematical projection
model and a limited number of 2D X-ray images are
employed for this purpose. Two successive
projections are used to compute the coordinates of a
3D contour.
The proposed scheme works as follows: after
extracting the contour of the proximal femur on the
2D X-ray images, comes the matching process. This
stage is a very important step for the 3D
reconstruction, because it impacts the accuracy of
the computed 3D coordinates. There exists several
works for contours matching (Park and Han, 1998;
Frenkel and Basri, 2003; Cui et al., 2009). For this
work we examine contour points matching using
merely the position and normal as features to
establish correspondences. The matching between
the points of two contours is performed with the
353
Akkoul S., Hafiane A., Leconge R., Lespessailles E. and Jennane R..
A 2D Matching Method for Reconstruction of 3D Proximal Femur using X-ray Images.
DOI: 10.5220/0004293403530357
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 353-357
ISBN: 978-989-8565-47-1
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

Euclidian 2D spatial distance then, the normals of
each point pairwise are used to filter the outliers.
This methods is simple and relatively efficient
allowing a good trade-off between accuracy and
computation complexity, which is important for our
application. The estimated point pairs are then used
to set up a set of 3D points. Since we are using
binary images, the correspondence of the contour 1
towards the contour 2 is not symmetric and may give
different results if contour 2 is used towards contour
1, thus the 3D reconstruction result may be different.
Here, we will discuss this issue and study its
influence on the 3D reconstructed models.
The obtained results, through the proposed
methodology, are benchmarked against real 3D CT
scan data to assess the accuracy of reconstruction.
The cadaver proximal femur was used as the
anatomy of interest throughout this study.
The paper is organized as follow: Section 2
presents the data. Follows the method and
experiments section that presents, the contours
extraction, contours matching, and estimating the 3D
coordinates.
2 MATERIALS
For this work we have used, a cadaver proximal
femur scanned with a resolution of 200µm by the
VISCOM X8060 NDT scanner. The bone was
placed on a rotating platform, between the x-ray
source and the sensor, and then 450 radiographs,
with a size of 1024×1024 pixels, were acquired on
360 degrees. Examples of the ex vivo proximal
femur radiographs are shown in Figure 1. Thanks to
these radiographs, and with the help of modern
computed tomography, the 3D mode allowed the
reconstruction of complete volumetric model of
911×806×711 voxels. Figure 2 shows the 3D model
of the reconstructed proximal femur. This model
serves as a ground truth to compare the
performances of the proposed algorithm.
In this study, eighteen 3D contours were
computed to reconstruct the 3D femur shape. Each
3D contour was estimated using 2 successive X-ray
images spaced by an angle of 8°. The step 8° was
chosen to realize the trade-off between the precision
and the matching process. In fact, if the two
projections are too close, this will generate more
errors for 3D coordinates estimation. And if the
projections are too far, a good matching between the
two contours will not be possible.
The next pair of X-ray radiographs was spaced
from the precedent one by an angle of 20°. This
way, we ensure including in the reconstruction a
minimum of information reflecting the different
forms of the proximal femur. The step 20
° between
two pairs of projections was chosen based on the
number of radiographs we wanted to use and to
improve the quality of the reconstruction.
0° 44°
92° 136°
220° 264°
292° 336°
Figure 1: X-ray images of the ex vivo proximal femur at
different angles.
3 METHOD AND EXPERIMENTS
Given few 2D X-ray images, our task is to establish
correspondence between the two input images. For a
given point of the edge identified in the first X-ray
image, the goal is to associate it to a point of the
edge identified in the second X-ray image. This
matching between points, on two different contours,
is realized using two criteria:
- The spatial distance: both associated points have to
be as close as possible to each other.
- Normals to the contours: the normals for both
associated points have to be in the same direction.
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
354

Figure 2: 3D ground truth of proximal femur used for the
test and reconstructed from 450 radiographs using X-ray
tomography reconstruction.
3.1 Bone Edge Extraction
The edge extraction is the first step of the 3D
reconstruction procedure. Despite that the good
contrast between the background and the femur in
the X-ray images, the accurate edge extraction is not
always a simple task. The nature of the x-ray
imaging makes the border fuzzy difficult to define
the real position of the edges. Whereas, the edge
localization determines the precision of the 3D
coordinates estimation. For that, various authors
have proposed semi-automatic or interactive
solutions to solve this problem (Laporte et al., 2003;
Le Bras et al., 2004).
To accurately detect the contour of a given
proximal femur, a morphology method is applied on
binarized X-ray images. The binarization step aims
at separating bone tissue (lighter) from pore and
background (darker) pixels. A standard binarization
method is applied (Chappard et al., 2008). This
method consists in determining a threshold based on
the local minimum between the two modes of the
histogram of each image.
Figure 3: Extracted edge corresponding to the image of
Figure 1.(0°) before applying the closing operation and a
zoom on the squared area in blue.
A morphological closing operation is then applied to
eliminate small contours considered as noise of the
segmentation step. The structuring element is a disk-
shaped of radius of 3 pixels. Figure 4 depicts an
example of the edge extraction.
Figure 4: Extracted edge corresponding to the image of
Figure 1.(0°) after applying the closing operation.
3.2 2D Matching Process
Let us denote the detected edge pixels in image1
(red edge, see Figure 5) as I1= {I
1
i
, i=0, 1... M-1}
and the detected edge pixels in image2 (green edge,
see Figure 5) as I2= {I
2
j
, j=0, 1, ..., N-1}, where M
and N are the number of the edge points detected in
image1 and in image2, respectively. Each point has
two features: the 2D coordinates (x, y) and the
normal vector at that position. The matching process
consists first in finding for each point in I1= {I
1
i
,
i=0, 1... M-1}, the closest one in I2, by computing
the Euclidean distance d as (1).
2
21
2
21
),(
jiji
yyxxyxd
(1)
The matching result is shown in Figure 5.
Figure 5: Matched points using the spatial distance and the
points coordinates.
As can be seen on Figure 5, many pairs of associated
points on the two contours have been found. To
improve the detection process, we propose to use an
additional criteria. For each retained pair of points,
the normals are estimated. If the normals are in the
same direction, these two points are retained,
otherwise they are rejected.
Figure 6 shows that using the distance and the
normals enable reducing the number of outliers
candidates pairs for the 3D reconstruction.
A2DMatchingMethodforReconstructionof3DProximalFemurusingX-rayImages
355
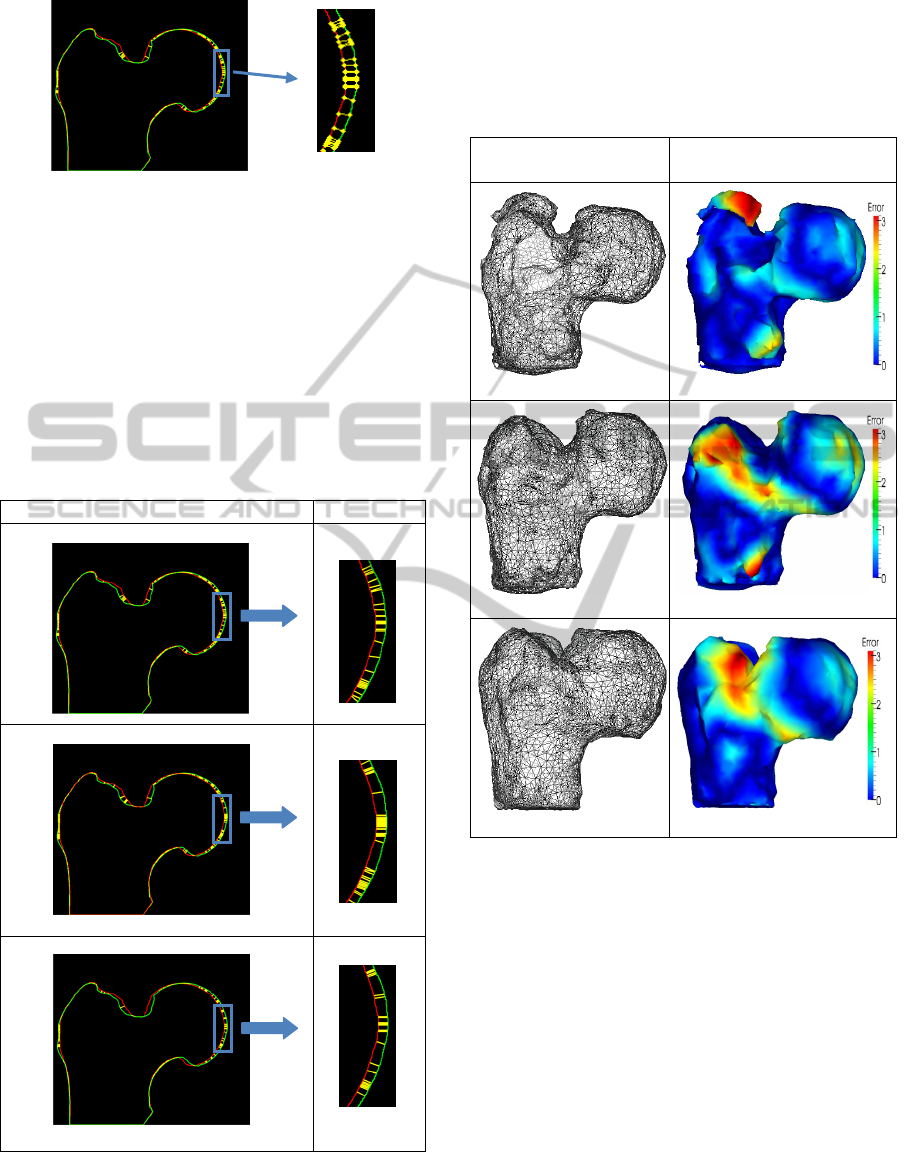
Figure 6: Matched points using the spatial distances and
the normals.
As mentioned in the introduction, since we are
dealing with binary images, the detected
corresponding points using the matching may differ
depending on the way of using the contours towards
each other. The matching is not symmetric.
Therefore, there are three cases of matching
directions:
(i) contour I1 toward contour I2,
(ii) contour I2 toward contour I1,
(iii) the intersection between the two directions.
Complete matching of all points Zoom
Figure 7: Matching after calculation of the distance and
the normals for the three cases. (i) edge I1 toward edge I2,
(ii) edge I2 toward edge I1, (iii) Intersection between (i)
and (ii).
The aim of the intersection technique is to keep the
pairs of points that are common in both matching
directions.
Figure 7 summarizes the obtained results for the
three cases.
Meshed shapes Errors comparing to the
ground truth
Figure 8: Meshed shapes and corresponding errors to the
ground truth. (i) edge I1 toward edge I2, (ii) edge I2
toward edge I1, (iii) Intersection between (i) and (ii).
Figure 8 presents the meshed shapes of the proximal
femur obtained from the reconstructed contours for
the three cases presented in Figure 7.
The estimated errors obtained in comparison to
the ground truth are presented too. These errors were
evaluated using the Metro tool for measuring error
on simplified surfaces (Cignoni et al., 1998). The red
and blue colors in the 3D reconstructed shapes
represent respectively the high and the low error
values. Errors are minimal in the case (c) where the
matching is performed in the two directions. This
demonstrates that the filtering of the outliers helps to
reduce the errors and increase the reliability of the
3D reconstruction technique.
(i)
(ii)
(iii)
(%)
(%)
(%)
(i)
(ii)
(iii)
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
356

4 CONCLUSIONS
This work shows that it is possible to recover the 3D
shape of the proximal femur from relatively small
number of X-ray projections. This was possible
thanks to x-ray stereo model, contour points
matching and combination of a round-trip scan to
exploit the different possibilities of estimating the
3D contours. As a prospect to this work, we would
like to reduce furthermore the number of the X-ray
images and improve the accuracy by exploring new
matching techniques as the Chamfer matching. The
incorporation of this whole system will help
providing enhanced 3D images for orthopedic
procedures and intra-operative assistance.
ACKNOWLEDGEMENTS
This work is part of the FRACTOS project
supported by the Region Centre (France). We
gratefully acknowledge the Region Centre for its
support.
REFERENCES
Baka, N., Kaptein, B. L., de Bruijne, M., van Walsum, T.,
Giphart, J. E., Niessen, W. J., Lelieveldt, B. P. F.,
2011. 2D-3D shape reconstruction of the distal femur
from stereo X-ray imaging using statistical shape
models. In Medical Image Analysis. 15(6):840-50.
Caponetti, L., Fanelli, A. M., 1993. Computed-aided
simulation for bone surgery. In IEEE Comput Graph
Appl. 13:86-92.
CGAL, Computational Geometry Algorithms Library.
http://www.cgal.org.
Chappard, C., Marchadier, A., Benhamou, C. L., 2008.
Side-to-side and within-side variability of 3d bone
microarchitecture by conventional micro-computed
tomography of paired iliac crest biopsies. Bone, Vol.
43, No. 1, Pages 203-208.
Cignoni, P., Rocchini, C., Scopigno, R., June 1998. Metro:
measuring error on simplified surfaces. In Computer
Graphics Forum, Blackwell Publishers, vol. 17(2), pp
167-174. Available at http://vcg.sf.net.
Cui, M., Femiani, J., Hu, J., Wonka, P., Razdan, A.,
January 2009. Curve matching for open 2D curves. In
Journal Pattern Recognition Letters. Volume 30 Issue
1, Pages 1-10.
Frenkel, M., Basri, R., 2003. Curve matching using the
fast marching method. Energy Minimization Methods
in Computer Vision and Pattern Recognition. Lecture
Notes in Computer Science Volume 2683, 2003, pp
35-51.
Gamage, P., Xie, S. Q., Delmas, P., Xu, W. L., 2011.
Diagnostic radiograph based 3D bone reconstruction
framework: Application to the femur. In Comput Med
Imaging Graph. 35(6):427-37.
Laporte, S., Skalli, W., De Guise, J.A., Lavaste, F.,
Mitton, D., 2003. A biplanar reconstruction method
based on 2D and 3D contours: application to the distal
femur. In Comput Methods Biomech Engin 6(1): 1-6.
Le Bras, A., Laporte, S., Bousson, V., Mitton, D., De
Guise, J.A., Laredo, J.D., Skalli, W., 2004. 3D
reconstruction of the proximal femur with low-dose
digital stereoradiography. In Comput Aided Surg 9(3):
51-7.
Park, J., S., Han J., H., 16 March 1998. Contour matching:
a curvature-based approach. In Image and Vision
Computing, Volume 16, Issue 3, Pages 181-189.
Whitmarsh, T., Humbert, L., De Craene, M., Del Rio
Barquero, L., M., Frangi, A., F., December 2011.
Reconstructing the 3D Shape and Bone Mineral
Density Distribution of the Proximal Femur From
Dual-Energy X-Ray Absorptiometry. In IEEE
Transactions on Medical Imaging, Vol. 30, No. 12.
Zheng, G., Gollmer, S., Schumann, S., Dong, X., Feilkas,
T., 2009. A 2D/3D correspondence building method
for reconstruction of a patient-specific 3D bone
surface model using point distribution models and
calibrated X-ray images. In Medical Image Analysis.
Volume 13, Issue 6, Pages 883–899.
A2DMatchingMethodforReconstructionof3DProximalFemurusingX-rayImages
357
