Planar Motion and Hand-eye Calibration using Inter-image

Homographies from a Planar Scene

arten Wadenb

ack and Anders Heyden

Centre for Mathematical Sciences, Lund University, Lund, Sweden

Keywords:

Visual Navigation, Planar Motion, SLAM, Homography, Tilted Camera.

Abstract:

In this paper we consider a mobile platform performing partial hand-eye calibration and Simultaneous Loc-

alisation and Mapping (SLAM) using images of the ﬂoor along with the assumptions of planar motion and

constant internal camera parameters. The method used is based on a direct parametrisation of the camera

motion, combined with an iterative scheme for determining the motion parameters from inter-image homo-

graphies. Experiments are carried out on both real and synthetic data. For the real data, the estimates obtained

are compared to measurements by an industrial robot, which serve as ground truth. The results demonstrate

that our method produces consistent estimates of the camera position and orientation. We also make some

remarks about patterns of motion for which the method fails.

1 INTRODUCTION

The development of algorithms for Simultaneous

Localisation and Mapping (SLAM) has been a ma-

jor focus in robotics research the past few decades.

Such algorithms aim at enabling a mobile platform to

explore and map its surroundings, while at the same

time maintaining accurate knowledge of its position.

Many types of sensors may be used to this end, and

are often combined to supplement each other.

For the mapping part of SLAM, a reconstruction

(broadly interpreted) must be created from the scene.

For some work on SLAM using visual sensors, see

for example (Davison, 2003), (Karlsson et al., 2005)

and (Koch et al., 2010). Scene reconstruction from

images is a well studied problem in computer vision,

and is still a very active research area. Since the intro-

duction of the fundamental matrix in (Faugeras, 1992)

and (Hartley, 1992), epipolar geometry has been the

foundation of many successful approaches to visual

reconstruction.

However, a planar or near-planar scene is well

known to be a degenerate or ill-conditioned case for

reconstruction based on the fundamental matrix and

similar approaches. Since planar scenes and objects

are very common in man-made or indoor environ-

ments, a navigation system intended to operate in

such environments must take care to avoid degener-

acy. Planar homographies, on the other hand, are par-

ticularly well suited to planar scenes, but are unable to

describe general 3D structure. This insight has been

utilised for visual navigation in (Liang and Pears,

2002) and (Hajjdiab and Lagani

ere, 2004), among

others.

In this paper we shall consider a single camera,

with square pixels and zero skew, moving at a con-

stant height above the ﬂoor. We will further assume

that the internal parameters of the camera are con-

stant, and that the camera orientation is ﬁxed except

for a rotation about the normal to the ﬂoor plane. Us-

ing inter-image homographies not only avoids the de-

generacy issue mentioned above, but in addition al-

lows us to use an explicit parametrisation of this par-

ticular kind of camera motion.

In the case where the inter-image homographies

describe a Euclidean (or, in general, an afﬁne) trans-

formation, the motion parameters are easily recovered

using the QR decomposition. This happens when the

image plane is parallel to the ﬂoor. In the presence of

a tilt, however, it is not as straightforward to extract

the motion information from the homographies. The

main contribution of this paper is a method to com-

pute both the tilt and the motion information from a

single homography.

Another reason for estimating the tilt is that only

rectiﬁed images may be stitched consistently into a

mosaic. A visual navigation system based on a sparse

feature based map of the ﬂoor plane also needs recti-

ﬁed images to construct the map. It is in general not

trivial to mount a camera with very high precision, so

164

Wadenbäck M. and Heyden A..

Planar Motion and Hand-eye Calibration using Inter-image Homographies from a Planar Scene.

DOI: 10.5220/0004293701640168

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 164-168

ISBN: 978-989-8565-48-8

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

avoiding the need for this would be useful.

Determining the tilt can also be seen as a partial

hand-eye calibration. The original formulation of the

hand-eye calibration problem was to recover the re-

lative orientation between a robot arm and a camera

mounted on the arm. Tsai and Lenz showed that with

known 3D feature points, known motion of the ro-

bot arm, and known transformations A and B, the un-

known relative orientation X can be determined from

the equation AX = XB (Tsai and Lenz, 1989). The

problem was later reformulated using quaternions to

parametrise rotations and 3 ×4 camera matrices in-

stead of classical transformation matrices (Horaud

and Dornaika, 1995).

2 CAMERA PARAMETRISATION

We assume that the camera is mounted rigidly onto a

mobile platform, and directed towards the ﬂoor. This

means that the position and orientation of the cam-

era can be parametrised by a translation vector t and

a rotation in the ﬂoor plane of an angle ϕ. The tilt

is described by the constant angles ψ and θ. Both

the translation and the three angles will be estimated.

The camera is assumed to move in the plane z = 0,

and the ground plane is taken to be at z = 1. This is

not a restriction, since it only reﬂects our choice of

the world coordinate system and global scale ﬁxation

(corresponding to the unknown focal length).

We will consider two consecutive images, A and

B, with associated camera matrices

= R

ψθ

[I | 0],

= R

ψθ

[I | −t].

(1)

Here R

ψθ

is a rotation of θ around the y-axis followed

by a rotation of ψ around the x-axis, and R

is a rota-

tion of ϕ around the z-axis (the ﬂoor normal).

Using (1), one can easily verify that the homo-

graphy H from A to B is

H = λR

ψθ

, (2)

for any non-zero λ ∈ R and with

T =





1 0 −t

0 1 −t

0 0 1





. (3)

3 TILT ESTIMATION

The presence of a tilt gives rise to perspective effects.

These distort the geometry perceived by the camera,

and prevent easy extraction of motion information. If

the tilt angles ψ and θ can be determined, one can

rectify the image and then use the QR decomposition

to retrieve the translation t and the free rotation ϕ.

To estimate ψ and θ, we derive equations that con-

tain these angles but which do not contain t and ϕ.

These equations will then be solved using an iterative

scheme.

3.1 Eliminating ϕ

Separating the tilt angles ψ and θ from the motion

parameters t and ϕ in (2), we get

ψθ

= λR

T. (4)

Here, one notes that R

can be eliminated by mul-

tiplying with the transpose from the left on both sides.

This results in the relation

ψθ

= λ

T, (5)

with (symmetric)

M =









= H

H. (6)

Since both sides of (5) are symmetric matrices,

one obtains six unique equations. Let L = R

ψθ

and R = λ

T be the left and right hand sides of

(5), respectively. Evaluating R , one obtains

R = λ





1 0 −t

0 1 −t

−t

1+ t





. (7)

3.2 Iterative Scheme

As described in Section 2, R

ψθ

= R

is a rotation

of θ around the y-axis followed by a rotation of ψ

around the x-axis. Direct multiplication of the ro-

tation matrices allows us to evaluate L (though this

margin is too narrow to contain the result), and one

ﬁnds that L is a fourth degree expression in c

cosψ, s

= sinψ, c

= cosθ and s

= sinθ.

Noting that R

, R

and R

are independent of t,

the equations for ψ and θ become



−L

= 0

. (8)

But instead of trying to solve (8) for both ψ and θ at

the same time, we will iteratively alternate between

solving for one angle, with the other held ﬁxed. This

reduces the problem of solving a fourth degree trigo-

nometric equation, so that we instead iterate and solve

a second degree equation in each iteration.

PlanarMotionandHand-eyeCalibrationusingInter-imageHomographiesfromaPlanarScene

165

Before explaining in detail how these equations

are solved, we ﬁrst outline in Algorithm 1 the iterat-

ive scheme which produces an approximation to R

ψθ

Since

ψθ

= R





0 −s

−s





(9)

it is trivial to ﬁnd ψ and θ from this approximation.

Algorithm 1: Iteratively approximate R

ψθ

. The steps on

line 6 and line 8 are detailed in Sections 3.2.1 and 3.2.2.

Since we “embed” into M the current approximation, we

may assume that the ﬁxed angle is zero when solving for

the free one.

Input: An inter-image homography H

Output: An approximation R of R

ψθ

M ← H

2: θ

← 0

3: R ← R

4: for j = 1, ..., N do

M ← R

j−1

6: Solve for ψ

M ← R

8: Solve for θ

9: end for

10: R ← R

···R

3.2.1 Solving for ψ

Since c

and s

cannot both be zero, (8) is equivalent











−L

= 0

. (10)

By letting

M = R

this can be written in matrix

form as





−

−2

−













= 0.

(11)

This means that (c

) lies in the null space of

the coefﬁcient matrix in (11). For the moment

, let us

assume that we expect a one dimensional null space.

Due to measurement noise this will not be the case, so

instead we use the singular vector v = (v

) cor-

responding to the smallest singular value as our null

vector.

This is true for most patterns of motion. Section 4.2

demonstrates some speciﬁc patterns of motions for which

this is fragile.

Provided the singular vector v one obtains ψ as

ψ =

arcsin

+ v

. (12)

3.2.2 Solving for θ

Now θ can be found in much a similar way as ψ.

Physical considerations imply that, at least for moder-

ately sized angles, R

has approximately the same

effect on the camera as R

. Examination of the

matrices conﬁrms this for small angles.

Therefore, if

M = R

, then











−L

= 0

, (13)

can be written in matrix form as





−













= 0. (14)

We ﬁnd, in the same way as in Section 3.2.1 that

the null vector v can be used to ﬁnd

θ =

arcsin

+ v

. (15)

4 EXPERIMENTS

In order to test how well the tilt estimation works in

practice, ﬁfty homographies of the form (2) were gen-

erated with random values for ψ, θ, ϕ and t. The true

angles and their corresponding estimates can be seen

in Figure 1.

4.1 Path Reconstruction

A simple path estimation has also been tried on both

synthetic and real data using the QR decomposition to

determine translation and planar rotation, after estim-

ating the tilt as described in Section 3. In the simu-

lation, noise of the magnitude corresponding to a few

pixels have been added to the points used to estim-

ate the homographies. Results for this experiment are

shown in Figure 2 and 3.

We have also carried out experiments with real

data. A camera mounted onto an industrial robot has

been used to take images, from which homograph-

ies were computed. The resulting reconstruction can

be seen in Figure 4. For comparison, we have ad-

ditionally estimated the non constant angle ϕ using

a method based on conjugate rotations, see (Liang

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

166

0 10 20 30 40 50

homography number

−15

−10

−5

θ (degrees)

estimated θ true θ

0 10 20 30 40 50

homography number

−20

−10

ψ (degrees)

estimated ψ true ψ

0 10 20 30 40 50

homography number

−150

−100

−50

100

ϕ (degrees)

estimated ϕ true ϕ

Figure 1: True and estimated values for ψ, θ and ϕ for ﬁfty

randomly generated homographies. As can be seen, the es-

timation works well in most instances.

0 5 10 15 20 25

homography number

−4.0

−3.5

−3.0

−2.5

−2.0

−1.5

−1.0

−0.5

0.0

ψ (degrees)

estimated ψ true ψ

0 5 10 15 20 25

homography number

2.5

3.0

3.5

4.0

4.5

5.0

5.5

6.0

6.5

θ (degrees)

estimated θ true θ

Figure 2: We see that the estimated values of ψ and θ are, on

average, close to the true values. Since ψ and θ are constant,

temporal ﬁltering could be used to get better estimates over

time.

−6 −5 −4 −3 −2 −1 0 1 2 3

true path estimated path

Figure 3: The simulated and the estimated paths. Procrustes

analysis has been carried out to align the path curves for

easy comparison.

and Pears, 2002) for details. This method computes

ϕ from the eigenvalues of the homography without

estimating the tilt. Figure 5 shows this estimate com-

100 200 300 400 500

x (mm)

−450

−400

−350

−300

−250

−200

−150

−100

y (mm)

true robot path

estimated robot path

Figure 4: True and estimated paths for the robot experiment.

At the lower part of the plot some erroneous estimates are

made, which results in the estimated path being deﬂected

away.

0 5 10 15

homography number

−15

−10

−5

ϕ (degrees)

proposed method

eigenvalue method

robot measurements

0 5 10 15

homography number

−2.5

−2.0

−1.5

−1.0

−0.5

0.0

0.5

1.0

error in ϕ (degrees)

proposed method

eigenvalue method

robot measurements

Figure 5: The upper plot shows the difference in orientation

between consecutive images, and the lower plot shows the

angular error. The plots show that our estimates of ϕ and the

eigenvalue-based estimates of ϕ are both close to the truth

(robot measurements).

Table 1: Mean, median and variance of the magnitude of

the angular error. For the eigenvalue-based method, meas-

urement 13 is considered an outlier and has been omitted.

Despite this, the proposed method is clearly seen to give

more accurate estimates.

Mean Median Variance

Proposed (QR) 0.2759 0.2467 0.0161

Eigenvalue 0.3947 0.4092 0.0403

pared to our estimate and the true value (as measured

by the robot). Both methods perform well, however

some statistical measures shown in Table 1 suggest

that tilt estimation followed by QR decomposition has

a slightly favourable performance.

PlanarMotionandHand-eyeCalibrationusingInter-imageHomographiesfromaPlanarScene

167

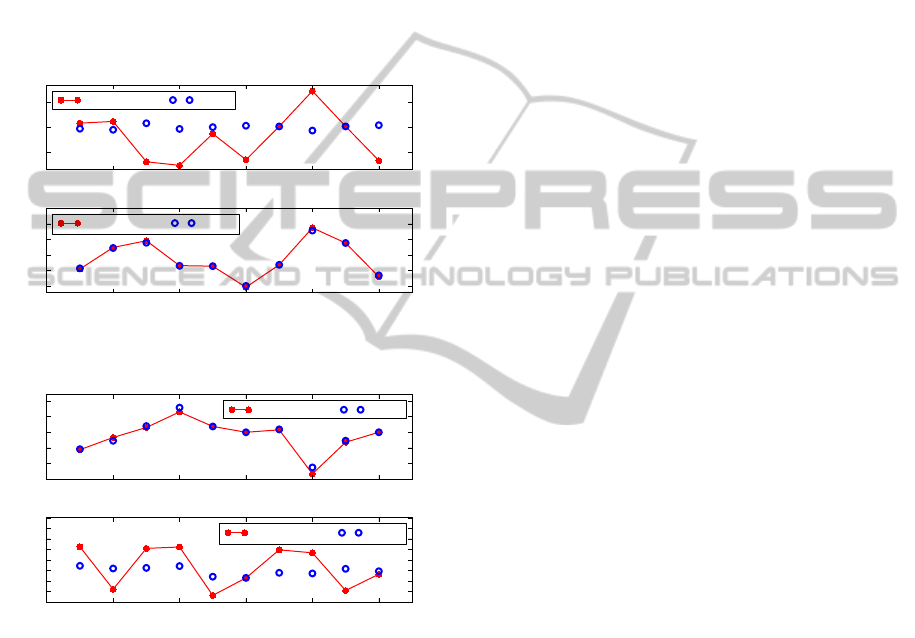
4.2 Ill-Conditioned Motion

Empirical evidence suggests that the instances where

the tilt estimation fails are the ones where the transla-

tion t is close to either a pure x-translation or a pure y-

translation. Randomly generating homographies with

this pattern of motion provides further evidence for

this. It can further be seen that a pure x-translation

gives rise to a poor estimate of ψ, while a pure y-

translation results in a poor estimate of θ. Results for

this experiment are presented in Figures 6 and 7. The-

oretical understanding of this will be necessary if the

instability is to be addressed.

0 2 4 6 8 10

homography number

−50

θ (degrees)

estimated θ true θ

0 2 4 6 8 10

homography number

−10

−5

ψ (degrees)

estimated ψ true ψ

Figure 6: When t is a pure x-translation, ψ seems to be

unreliably estimated.

0 2 4 6 8 10

homography number

−15

−10

−5

θ (degrees)

estimated θ true θ

0 2 4 6 8 10

homography number

−30

−20

−10

ψ (degrees)

estimated ψ true ψ

Figure 7: When t is a pure y-translation, θ seems to be un-

reliably estimated.

5 CONCLUSIONS

Tilt estimation is a prerequisite for constructing con-

sistent ﬂoor maps using images from a tilted camera.

In this paper we have presented an iterative scheme

for determining the tilt from a single homography.

Experiments with a simple path reconstruction have

been conducted, which show that if the tilt is rectiﬁed

then the correct Euclidean motion can be found using

the QR decomposition. Experiments using synthetic

data show that the estimated tilt angles are close to

the true tilt angles in most instances, however some

especially troublesome motions have been found.

ACKNOWLEDGEMENTS

This work has been funded by the Swedish Founda-

tion for Strategic Research through the SSF project

ENGROSS, http://www.engross.lth.se.

REFERENCES

Davison, A. J. (2003). Real-Time Simultaneous Localisa-

tion and Mapping with a Single Camera. In Proceed-

ings of the Ninth IEEE International Conference on

Computer Vision, volume 2 of ICCV ’03, pages 1403–

1410, Nice, France. IEEE Computer Society.

Faugeras, O. D. (1992). What can be seen in three dimen-

sions with an uncalibrated stereo rig? In Proceedings

of the Second European Conference on Computer Vis-

ion, volume 588 of ECCV ’92, pages 563–578, Santa

Margherita Ligure, Italy. Springer-Verlag.

Hajjdiab, H. and Lagani

ere, R. (2004). Vision-Based Multi-

Robot Simultaneous Localization and Mapping. In

CRV ’04: Proceedings of the 1st Canadian Confer-

ence on Computer and Robot Vision, pages 155–162,

Washington, DC, USA. IEEE Computer Society.

Hartley, R. I. (1992). Estimation of Relative Camera Po-

sitions for Uncalibrated Cameras. In Proceedings of

the Second European Conference on Computer Vision,

volume 588, pages 579–587, Santa Margherita Ligure,

Italy. Springer-Verlag.

Horaud, R. and Dornaika, F. (1995). Hand-Eye Calib-

ration. International Journal of Robotics Research,

14(3):195–210.

Karlsson, N., Bernardo, E. D., Ostrowski, J. P., Goncalves,

L., Pirjanian, P., and Munich, M. E. (2005). The

vSLAM Algorithm for Robust Localization and Map-

ping. In ICRA ’05: Proceedings of the 2005 IEEE In-

ternational Conference on Robotics and Automation,

pages 24–29, Barcelona, Spain. IEEE.

Koch, O., Walter, M. R., Huang, A. S., and Teller, S. J.

(2010). Ground Robot Navigation using Uncalibrated

Cameras. In ICRA ’10: IEEE International Confer-

ence on Robotics and Automation, pages 2423–2430,

Anchorage, Alaska, USA. IEEE.

Liang, B. and Pears, N. (2002). Visual Navigation using

Planar Homographies. In ICRA ’02: Proceedings of

the 2002 IEEE International Conference on Robot-

ics and Automation, pages 205–210, Washington, DC,

USA.

Tsai, R. and Lenz, R. (1989). A New Technique for Fully

Autonomous and Efﬁcient 3D Robotics Hand/Eye

Calibration. IEEE Transactions on Robotics and Auto-

mation, 5(3):345–358.

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

168