SODA: A Scalability-Oriented Distributed & Anticipative Model for

Collision Detection in Physically-based Simulations

Steve Dodier-Lazaro

1,3

, Quentin Avril

2,3

and Val

erie Gouranton

1,3

INSA de Rennes, Rennes, France

Universit

e de Rennes 1, Rennes, France

IRISA / INRIA, Rennes, France

Keywords:

Collision Detection, Physically-based Simulation, Distributed Systems, Scalability, Optimistic Computing.

Abstract:

In this paper, we propose a distributed and anticipative model for collision detection and propose a lead for

distributed collision handling, two key components of physically-based simulations of virtual environments.

This model is designed to improve the scalability of interactive deterministic simulations on distributed sys-

tems such as PC clusters. Our main contribution consists of loosening synchronism constraints in the collision

detection and response pipeline to allow the simulation to run in a decentralized, distributed fashion. To do

so, we setup a spatial subdivision grid, and assign a subset of the simulation space to each processor, made of

contiguous cells from this grid. These processors synchronize only with their direct neighbors in the grid, and

only when an object moves from one’s area to another. We rely on the rarity of such synchronizations to allow

anticipative computing that will also work towards improving scalability. When synchronizations occur, we

propose an arrangement of collision checks and rollback algorithms that help reduce the processing cost of

synchronized areas’ bodies. We show potential for distributed load balancing strategies based on the exchange

of grid cells, and explain how anticipative computing may, in cases of short computational peaks, improve

user experience by avoiding frame-rate drop-downs.

1 INTRODUCTION

Virtual reality [VR] researchers and industry users

have growing needs for the physically realistic sim-

ulation of large virtual environments. These include

detecting collision between simulated bodies. Colli-

sion detection [CD] consists of ﬁnding if, where and

when several objects may collide in a 3D virtual envi-

ronment (Ericson, 2005). It is a prerequisite of colli-

sion response [CR] that will provide the proper forces

or impulses to be applied on the bodies by means of

Constraint Solving [CS].

Considerable research effort has been put in col-

lision handling in general, and many algorithms and

frameworks exist for sequential and parallel collision

detection and constraint solving. Current parallel col-

lision detection or handling systems are based on the

traversal and update of tree structures (Tang et al.,

2009; Thomaszewski et al., 2008), the use of GPUs

for massively parallel processing (Kim et al., 2009;

Pabst et al., 2010), or ﬁne-grained scheduling strate-

gies (Hermann et al., 2009).

Coupled with powerful computers, these algo-

rithms already allow real-time large-scale simulation

of increasingly complex bodies. Besides, theoretical

grounds exist on the distribution of a virtual environ-

ment simulation (Fujimoto, 1999), and we are now

in a time where PC clusters are affordable for most

research centers and large companies, and are already

used for animation and rendering in VR systems (Raf-

ﬁn and Soares, 2006).

Nevertheless, little work has been done towards

collision handling on distributed systems. Current

research addresses collision detection between bod-

ies in high-latency networks (Chen and Verbrugge,

2010), rather than the fully distributed scheduling of

a collision pipeline. (Morgan and Storey, 2005) dis-

tributed collision handling in the past, but also with

a focus on avatars controlled by multiple users rather

than handling collisions distributedly without dupli-

cates. We argue this would beneﬁt the performance

of applications like distributed simulation of virtual

cities, or massively multiplayer online games with

more persistent and realistic physics.

Contributions. We present SODA, a model for colli-

337

Dodier-Lazaro S., Avril Q. and Gouranton V..

SODA: A Scalability-Oriented Distributed & Anticipative Model for Collision Detection in Physically-based Simulations.

DOI: 10.5220/0004293803370346

In Proceedings of the International Conference on Computer Graphics Theory and Applications and International Conference on Information

Visualization Theory and Applications (GRAPP-2013), pages 337-346

ISBN: 978-989-8565-46-4

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

sion detection on distributed systems with anticipative

computation. SODA aims for interactive physically-

based simulation on PC clusters. We propose loosely-

synchronized and anticipative simulation by dividing

space into areas called worlds. Each world is se-

quentially simulated on a stand-alone core (or multi-

core node). We allow anticipative computation (i.e.

simulating steps ahead of the current clock of other

worlds) when no data dependency prevents it. We

outline methods for synchronizing collision detection

and constraint solving when a dependency exists, and

we propose rollback algorithms that reduce the cost of

synchronizing a simulation step between worlds when

that step had been anticipatively computed. Finally,

we explain how anticipation can help improve user

experience by avoiding sharp decreases of frame-rate

when computationally expensive collisions occur.

Organization. In Section 2, we review some paral-

lel and distributed CD and particle simulation algo-

rithms, and explain our positioning. In Section 3, we

describe our distributed and anticipative virtual envi-

ronment simulation model. Section 4 presents ob-

servations made on a case study of collision detec-

tion. They may guide implementation choices for spa-

tial subdivision granularity and distributed CS design.

They also outline the beneﬁts of anticipation. Finally,

we conclude and propose leads for future research in

Section 5.

2 RELATED WORK

In this section, we present state-of-the-art CPU-based

parallel collision handling systems. We do not investi-

gate GPUs, used as massively parallel side processors

in both CD and CS, as they are not relevant to our in-

tent in SODA: assessing the feasibility of distributed

rather than centralized parallel collision detection.

We also outline the difference between existing

distributed CD methods and SODA, and introduce

distributed particle simulation algorithms. Finally, we

enumate the assumptions our model is based on.

2.1 Parallel Collision Handling

Parallel and distributed systems are nowadays targets

of choice for virtual reality applications with signiﬁ-

cant computing needs, and there is ﬂourishing litera-

ture on parallel collision handling. Yet, no distributed

approach has been proposed for consistent, determin-

istic CD. Many researchers have instead sought to

take better advantage of particular architectures such

as combinations of CPUs and GPUs (Hermann et al.,

2010; Kim et al., 2009; Pabst et al., 2010). The pa-

pers we present focus on lowering synchronization

and load balancing costs in a multi-CPU context, and

are the closest in philosophy with SODA.

(Hermann et al., 2009) explored the construction

of a task dependency graph for the collision handling

pipeline based on previous collisions, which allowed

them to schedule tasks among available processors

and eliminated the need for synchronization between

each pipeline stage. The graph is replayed among

several time frames to limit the overhead of load bal-

ancing. They reached close to optimal scalability for

particle simulation, but not for simulations containing

heterogeneous complex objects.

(Tang et al., 2009) proposed incremental parallel

BVTT traversal, measuring the workload per BVTT

branch to distribute the load between processors in

collision detection. They decompose BVTT traversal

as a pipeline mostly made of parallel steps, albeit with

synchronization between each stage. They achieved

a speedup up to 6 fold on an eight core CPU, after

which performance stopped increasing linearly. Be-

sides, tree-based spatial subdivisions need to be regu-

larly updated, which is difﬁcult in a distributed way.

Finally, (Kim et al., 2008) reached 7.3 speedup

on 8 CPUs over a single core, with their PCCD al-

gorithm which is based on dynamic task decomposi-

tion and assignment. They reach such scalability by

getting rid of as many data dependencies and synchro-

nizations as possible in their pipeline. They presented

the best scalability in the CD literature. For compari-

son, Hermann et al.’s physics simulation pipeline has

a slightly lower scalability when simulating heteroge-

neous rigid bodies on sixteen cores.

2.2 Distributed Collision Detection

Typical peer-to-peer applications include multiplayer

games, featuring a virtual environment in which

avatars may collide. These avatars are controlled on

different computers, which need to exchange infor-

mation in order to process collisions and keep the

state of the environment consistent. Deterministic CD

is not realistic in this high-latency network context

because packets may be lost or take hundreds of mil-

liseconds to reach all hosts.

Various strategies emerged for CD with remote

bodies, usually variants of Dead Reckoning [DR]

which predicts the motion of remote avatars until

they update their real position (Fujimoto, 1999). For

instance, Motion-Lock (Chen and Verbrugge, 2010)

predicts collisions and starts agreement with remote

hosts before the collisions occur, rather than once re-

mote hosts communicated updated body positions.

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

338

In SODA however, it is the simulation that is dis-

tributed on several cores and not the sources of user

interaction. We are interested in precise, determinis-

tic CD. SODA could be used for complex physically-

realistic virtual city simulations with one or several

agents. In contrast, previous work focuses on virtual

worlds where each node can process all physics con-

straints on its own.

2.3 Distributed Particle Simulation

Particle simulation researchers have common re-

search questions with the collision detection commu-

nity: they need to detect and process collisions be-

tween thousands of objects in a simulated environ-

ment. However, particles are typically represented as

points or spheres, rather than thousands-of-polygons

bodies. This allows the use of much simpler CD algo-

rithms, and signiﬁcantly simpler load balancing met-

rics. Therefore, particle simulation systems are usu-

ally run on clusters aggregating hundreds of cores.

(Li et al., 2007) proposed an event-driven parti-

cle collision system with a priority queue of events to

be processed for each particle. Speculative compu-

tations are performed on particles waiting for a prior

event to be processed. These speculative computa-

tions are kept if the states of particles they are per-

formed on have not been affected by prior events in

the queue. They also proposed a dynamic adjustment

of the amount of speculative computation to perform

depending on how many of these are invalidated, in

order to save storage and computation costs.

(Miller and Luding, 2004) proposed a spatial sub-

division based on a uniform grid, where each CPU

manages an area of contiguous, square-shaped cells

to best exploit spatial coherence. They add border

traversal events to their system to know when syn-

chronization between two areas is necessary. Finally,

they perform dynamic load balancing by splitting an

overloaded area, merging two underloaded areas, and

assigning one of the splitted sub-areas to the orphan

core.

2.4 Work Hypotheses

Scalability is limited in a parallel computing system

by the lack of task decomposition that prevents from

using all available nodes, or by recurrent synchroniza-

tions. The former problem may be solved by decom-

positing tasks further, and scheduling them according

to their dependencies. This has been largely done in

CD and CR.

The latter may be managed with optimistic com-

puting: if the slowest node’s tasks cannot be split

any further, other nodes will anticipate their work-

load to obtain speed improvements onto next compu-

tation steps. However this will bring beneﬁts only if

the slowest node is not always the same.

We argue that this condition may be veriﬁed in a

range of VR applications (e.g. those with constantly

moving bodies such as factory automated assembly

lines, or virtual cities with moving crowds). A dis-

tributed (inherently anticipative) system may improve

performance for such applications.

Asanovic et al. (Asanovic et al., 2006) advise re-

searchers to design systems that scale well on any

number of cores. In practice, simulations imply tem-

poral coherence and hence synchronization at some

point, which means they cannot scale inﬁnitely. Like-

wise, beneﬁts from optimistic computing are theoret-

ically bounded (Miller and Luding, 2004), on top of

additional memory cost (Fujimoto, 1999).

Knowing this, improving the performance of some

tasks of the collision handling pipeline (such as us-

ing GPUs to dramatically improve CD or CS) will

bring beneﬁts, but pushing further scalability limits of

the global pipeline by removing unnecessary synchro-

nizations may bring other, complementary beneﬁts.

3 THE SODA MODEL

In this section, we describe how space is distributed

and synchronization occurs in SODA. We also present

our approaches to I/O management, and a sketch of

distributed load balancing algorithm.

We propose to loosen synchronization constraints

between the main components of collision handling

pipelines, by dividing the simulation space and allow-

ing the computation of different simulation steps in

either of these areas. In contrast, current frameworks

never start a simulation step’s CD before CS and time

integration have been entirely performed for the pre-

vious step.

In SODA, each node processes a subset (referred

to as a world) of the simulation space, deﬁned by ad-

jacent cells in a spatial subdivision uniform 3D grid

(named territory). Each world communicates exclu-

sively with those managing areas adjacent to his own

(called neighbors, and the planes between distinct ar-

eas are called borders).

Worlds synchronize with neighbors when a body

overlap the border between their territories. Only

the CS stage on the simulation island of the border-

crossing body needs to be performed concurrently by

worlds. However, they also exchange data during CD

to identify common simulation islands.

Each world saves the results of simulation steps

SODA:AScalability-OrientedDistributed&AnticipativeModelforCollisionDetectioninPhysically-basedSimulations

339

Figure 1: A 2D simulation with three worlds. On the right,

a border traversal forces the top worlds to synchronize.

into a buffer. A process then reads entries correspond-

ing to the slowest world’s clock, to allow output to

users. User input can be managed by modifying the

world containing bodies with which the user interacts.

Rollback algorithms can be used to integrate user ac-

tions in the world’s buffer entries.

In this paper, we do not investigate issues linked

to user interaction or to predictability of body motion

which may impact ofﬂine computation of data struc-

tures or scheduling strategies. In SODA, initial terri-

tories are modiﬁed with time by load balancing.

3.1 Territories and Borders

3.1.1 Territory Deﬁnition

We deﬁne spatial subdivision in the form of a uniform

3D grid, which has the following advantages in a dis-

tributed context:

• cells can be described with just coordinates and

a world identiﬁer, allozing compact exchange of

cell data between worlds

• storing the topology of the subdivision is very

cost-efﬁcient (no need to store shapes)

• unlike tree-like subdivisions, they do not require

to update their shape on body motion (but may

have to on body deformation)

Worlds manage a territory made of adjacent grid

cells so as to best exploit temporal coherence (Lin and

Gottschalk, 1998). Hence, bodies switching between

cells will most often remain in the same world. This

avoids creating data dependencies between worlds

when a body moves from one to another.

Another advantage of this territory deﬁnition is

that worlds need to hold in memory just the grid of

their territory and direct surroundings (to keep track

of which cells belong to which neighbors).

The problem of optimal cell size is well-known

and does not have an ideal solution (Le Grand, 2007).

The size of grid cells depends in SODA upon a sin-

gle criterion: cells should be strictly larger than the

biggest simulated body in order to ensure that colli-

sions only occur between bodies from adjacent cells.

The use of hierarchical grids is left for further re-

search, to support bodies with heterogeneous dimen-

sions or deformable shapes.

3.1.2 Border Traversal Detection

Collisions may occur between bodies from different

worlds, as illustrated in Figure 1. If they are left un-

managed, then some contact responses will not be ap-

plied and the simulation will no longer be determinis-

tic. To allow anticipation within a world, we need to

be able to detect which bodies overlap a border.

To do so, borders between two territories are rep-

resented by static physics bodies and SODA’s detec-

tion collision algorithm is used to discover border

traversals, although no collision response is applied

with border bodies. The synchronization mechanism

is explained in Section 3.2.2.

Cost of the Detection. Assuming territories are made

of a single cell, every body will have to be tested for

collision with the 6 borders of its containing cell. In

the worst case, all bodies will be next to their cell’s

corner and collide with 3 borders. Hence they may

overlap with up to 7 distinct worlds, which brings up

to 9 more borders with which they may be colliding.

The sum of additional collision checks to perform, ﬁf-

teen per body, remains of linear complexity.

In practice, territories are larger and fewer cells

contain borders. Besides, overlapping tests with

an axis-aligned plane are often faster than collision

checks between two complex bodies, further limiting

the cost of border detection.

3.2 Autonomous Worlds

3.2.1 Worlds and Transform Buffers

Worlds in SODA are physics engines that run sequen-

tially on a node. They are responsible for detecting

and processing collisions in a subset of the simula-

tion space. Each engine uses its own local clock and

performs simulation steps independently from others.

The results of a simulation step are made available to

others as a time-stamped list of transforms (i.e. mo-

tions, rotations and velocities of bodies) for each body

simulated in the world’s territory. The lists are saved

to a circular buffer, which can be read to retrieve the

positions of bodies at each step.

The use of a circular transform buffer offers a

trade-off between the desired robustness of the ap-

plication and the memory size needed to store the

buffers. A large buffer enables the precomputation of

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

340

World j

i+1

i+2

i+3

i -1

j -1

j+1

j+2

j -2

K+2

K+1

K+3

K+4

World k

Transform Buﬀer Interface: queries all worlds

for object transforms at the slowest world's time

World i

3D Engine

Figure 2: Global architecture of SODA. Worlds i, j and k’s

buffers are read by the interface, which is used by the 3D

engine’s process to update positions.

several seconds of simulations, which can help absorb

the performance impact of a computational peak due

to many simultaneous collisions. Yet, the size of the

buffer must be bounded depending on the amount of

memory available on the system where SODA runs.

Besides, the more important the anticipation is, the

more likely it is to be invalidated by further synchro-

nizations, up to a point where anticipation becomes

pointless (Miller and Luding, 2004).

A buffer interface is in charge of reading and

deleting buffer entries, at the same timestamp for all

worlds. It updates body representations within a 3D

engine, to allow output to users, and also to make sure

no entry within a buffer is deleted before all worlds

have simulated the corresponding timestamp (since it

may be modiﬁed by unexpected synchronization).

3.2.2 Synchronization with Neighbors

Determinism is guaranteed in traditional parallel col-

lision handling frameworks by not performing antic-

ipation: all constraints from a simulation step are

solved before the next step starts. Instead, we want

to guarantee it by taking into account data dependen-

cies between worlds at different times.

Consequently, any body that overlaps a border be-

tween two worlds will cause these worlds to synchro-

nize their physics pipeline. When two worlds are

synchronized, they will exchange information about

border-crossing bodies, and make sure to take into ac-

count collisions between foreign border-crossing bod-

ies and their own ones. Simulation islands are then

computed from collision information.

If a body overlaps a border and exists in two is-

lands on different worlds, the islands will be merged

before computing a response in parallel. Otherwise,

islands that exist within a single world (a fortiori

those that don’t contain bodies on border cell) are

solved locally on a world’s node.

Algorithm 1 presents our new collision handling

pipeline. First, CD is performed between local bod-

ies, then with the world’s borders. In case of synchro-

nization (border traversal or external query), worlds

will exchange their lists of crossing bodies, and de-

tect collisions between these new bodies and theirs.

Simulation islands can then be computed and

merged with foreign ones when they contain a for-

eign body. The local ones may be solved locally and

the mixed ones in parallel between involved worlds.

Nothing prevents from starting local CS before

foreign collisions are detected. Synchronization mes-

sages can be read asynchronously by their recipient,

and a world ahead of another one for any stage of the

pipeline could use the rollback algorithms presented

after to avoid processor idling caused by synchroniza-

tion.

3.2.3 Modifying Anticipated Entries

A direct consequence of synchronization between two

worlds w

and w

is that the world that is ahead of the

other has to modify some of its anticipated compu-

tations: they were performed ignoring a data depen-

dency from the slower world and some collisions need

to be integrated.

In order to limit the incurred losses, we propose

a CD rollback based on the spatial subdivision grid

used for territories. We integrate changes caused by

the synchronization into previously computed buffer

entries, using algorithm 2: Rollback and Propagate.

The worst use case of SODA, performance wise,

is a simulation where all bodies are constantly inter-

connected. This will force constant synchronization

between all worlds and prohibit anticipation. We yet

have to evaluate the overhead caused by the use of

SODA in such a setup, but SODA is likely to be out-

performed by ﬁner-grained parallel solutions for this

kind of simulations. We expect to be able to improve

performance in the future by ﬁnding other ways of

performing anticipative computations.

The rollback algorithm will improve performance

over direct invalidation of a full entry whenever not a

territory contains several simulation islands. Indeed,

we already use a spatial subdivision broad-phase to

allow cheap border traversal detection. The cost of

this broad-phase lies in the actual overlap tests be-

tween bodies and not in the browsing of the subdivi-

sion cells. Hence, the rollback algorithm will not be

signiﬁcantly costlier than a broad-phase with ordered

cell browsing, and will be more efﬁcient as soon as

some bodies are not in a chain of contacts with the

SODA:AScalability-OrientedDistributed&AnticipativeModelforCollisionDetectioninPhysically-basedSimulations

341

Input: TimeStamp t

Variables:

List of ContactInfo borderCols;

List of Worlds nbh;

boolean syncNeeded = ⊥

Code:

localCD();

borderCols = onBorderCD();

if borderCols not empty then

nbh =

findAndNotifyNeighbors(borderCols);

syncNeeded = >;

end

if syncQueue contains entry for t then

borderCols = borderCols ∪

syncQueue.getBorderCols(t);

nbh = nbh ∪ syncQueue.getWorlds(t);

syncNeeded = >;

end

if syncNeeded then

waitForNeighbors(nbh, t);

foreach World n ∈ nbh do

exchangeBorderCollisions(n,

borderCols, t);

end

foreach ContactInfo info ∈ borderCols do

singleBodyCD(info.getBody());

end

calculateSimulationIslands();

mergeIslandsWithBorderCols(nbh, t);

parallelSolveMergedIslands(nbh, t);

concurrently with

solveLocalConstraints();

else

calculateSimulationIslands();

solveLocalConstraints();

end

Algorithm 1: Collision handling pipeline with synchroniza-

tion on border traversal.

ones that cross a border. Figure 3 shows a ﬁctive ex-

ample of rollback applied to a buffer entry. Only the

bodies in the darker cells will have their transforms re-

computed, and because they do not collide with bod-

ies from surrounding cells, the rest of the entry will

be preserved.

Rollback may also be developed for CS, by saving

result matrices of commonly used iterative solvers,

and by later modifying them by adding extra con-

straints. Because the matrix will be close to conver-

gence for almost all values (except for the non-null

lines and rows of the new constraints), it may con-

verge with less iterations than from starting over. This

technique is already used to decompose systems and

solve them in parallel on GPUs (Tonge et al., 2012).

However, it provides beneﬁts only from direct

Input: Stack of Bodies L, TimeStamp t

Variables:

List of Bodies temp, colliding;

CircularTransformBufferEntry newEntry;

Body bd;

if LocalClock() ≥ t then

Code:

m Buffer.rollbackAt(t);

while t < LocalClock() do

while L not empty do

bd = L.pop();

temp = rebuildIsland(o);

colliding = {temp} ∩ colliding;

end

rollbackSolveConstraints(colliding);

foreach Body bd ∈ colliding do

newEntry.insert(o.getTransform());

end

m Buffer.overwrite(t, newEntry);

L = colliding;

colliding = {};

t = t+1;

end

Algorithm 2: Our rollback algorithm, presented with-

out synchronization mechanisms for easier understand-

ing. rollbackAt() prevents from reading the buffer

starting at t, and overwrite() overrides the entry and

makes it readable again. rebuildIsland() performs

CD body per body until no more collisions are found.

rollbackSolveConstraints() reuses a previous matrix

if possible to accelerate CS.

rollback of the ﬁrst step where synchronization oc-

cured. Typically, many values will be (slightly) af-

fected in the new result matrix, making it impossible

to directly modify next step’s matrix in the same way.

It is left to future research to determine how to reuse

result matrices from previous simulation steps.

Differences with Dead Reckoning. DR answers a

need in high-latency environments, that SODA is un-

able to deal with. Still, it is worth noticing that the

CS part of the pipeline beneﬁts from our border de-

tection, in case of mistake during anticipated compu-

tations. Figure 4 shows that SODA will never detect

false collisions when a foreign body’s motion is not

known for a given simulation step. Instead, it will ig-

nore the (potential) foreign body until the rollback al-

gorithm is called. This means that no false constraint

has been injected in the constraint equation system (as

would happen with estimations of remote body po-

sition), and this is primordial to allowing the reuse

of past computed matrices. In SODA, false positives

may only occur indirectly, when a rollback removes a

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

342

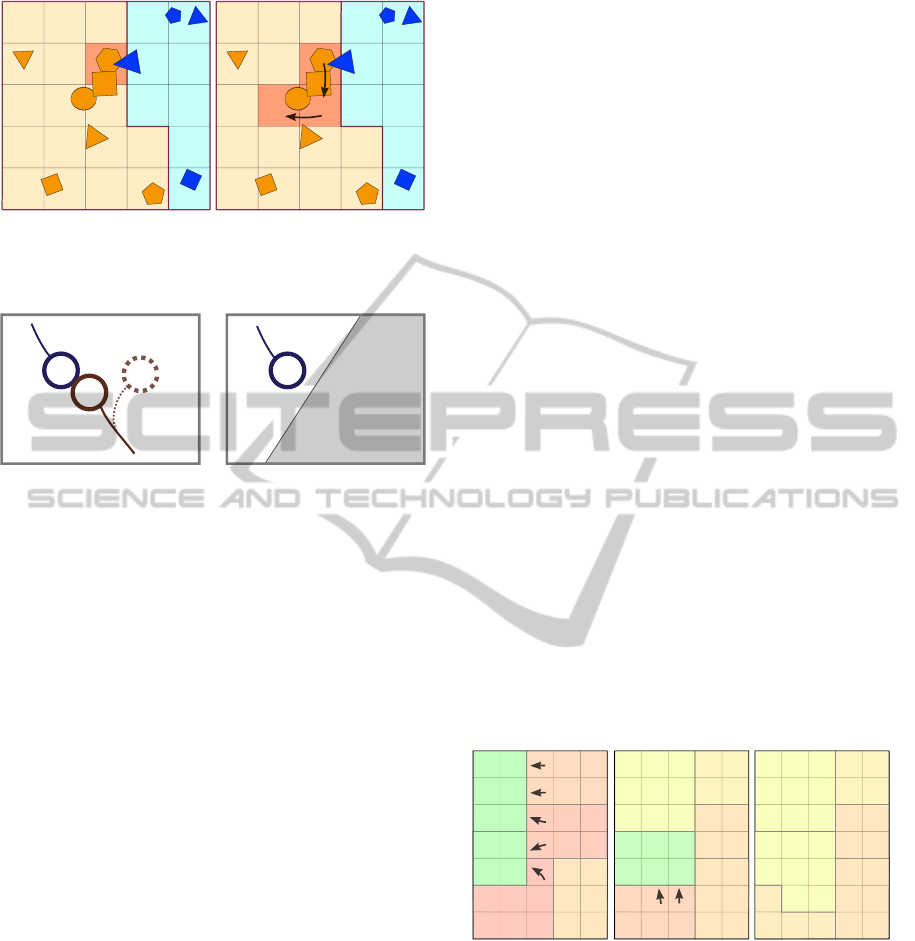
Figure 3: Example of rollback on the left world, caused

by a synchronization. Only bodies in the border-traversing

body’s simulation island will be modiﬁed.

L L

Dead Reckoning SODA Anticipation

real

estimate

ignored until

border collision

Figure 4: DR-like strategies may detect false positive that

will prevent CS rollback, whereas SODA will avoid them.

border traversal that also caused a collision.

3.3 Input/Output and Simulation Setup

3.3.1 Rendering

Interactive applications need real-time rendering, re-

gardless of simulation progress. In SODA, a 3D en-

gine stores its own clock and 3D representation of

bodies, and updates them before each rendering pass

with a buffer interface (as illustrated by Figure 2).

This interface is queried with the clock value of

the step to render, and then asks all worlds if they

have a buffer entry for this value. If not, the inter-

face uses the lowest clock value available among all

worlds. Then, it actually queries entries and updates

the 3D engine’s body information accordingly. It also

returns the engine the clock value that was used, so

that rendering occurs in real time when worlds cope

with the workload, and in slow motion otherwise.

The cost of reading transforms is linear in num-

ber of bodies and no worlds are created or removed

during the simulation. On large clusters where buffer

reading may not scale, it is thus possible to distribute

the querying and reading of entries onto several cores

that will concurrently access the 3D engine’s internal

memory. They can negotiate the clock value to use

and the worlds each one of them should monitor.

3.3.2 User Input

Users may interact with an application by adding, re-

moving, or modifying the behavior of a body. Either

way, the modiﬁcations that occurred will cause the in-

validation of anticipated simulation steps in a world.

The rollback algorithm can be used to manage these

changes. The overhead of integrating user interac-

tions in anticipated computations cannot be avoided

but is lesser than that of full invalidation.

3.4 Load Balancing

To validate our model, we must be able to balance

load between nodes in a distributed fashion as well.

In this section we just show that there are ways of de-

signing distributed load balancing for SODA. For in-

stance, this may be performed between two worlds by

asking for and by giving parts of their territory. When

a cell is transferred from a world to another, its bodies

are then simulated by the recipient world, increasing

the runtime of its collision handling pipeline, and re-

ducing the load of the sender world. A rough sketch of

the load balancing process is illustrated by Figure 5.

There are several challenges to address for efﬁ-

cient load balancing: using lightweight, accurate and

distributed load estimation metrics; choosing which

grid cells should be given, and to which neighbors;

keeping territories shaped as spheres or cubes to pre-

serve beneﬁts from temporal coherence (Miller and

Luding, 2004); performing loose load balancing to

limit its cost and rely more on anticipation.

39%

54%

64%

82%

73%

24%

32%

81%

92%

89%

73%

54%

64%

69%

73%

Figure 5: Example of two underloaded worlds, p

and p

being given territory by their overloaded neighbors (per-

centages represent load estimations).

3.4.1 Load Metrics

Simple metrics, such as the average time to perform

one pass of collision handling, can be combined with

the advance of a world over its neighbors, which in-

dicates how much it can afford to handle collisions

more slowly. We could also use the density of the

territory, as it represents the risk that a computational

peak occurs. The problem of computing an average

SODA:AScalability-OrientedDistributed&AnticipativeModelforCollisionDetectioninPhysically-basedSimulations

343

load, or of estimating one’s load, in a distributed con-

text can be expressed as a consensus problem and is

widely studied. A summary of current challenges and

advances can be found in the PhD thesis of (Cosenza,

2010), with examples in ray-tracing and simulation.

3.4.2 Example of Load Balancing Algorithm

Every world may compute, using the metrics, a global

load estimation, as well as an estimation for each of

its cells. It may then ask its neighbors for their own

last load estimation. If the world is signiﬁcantly more

loaded, it will compute a load score to reach, repre-

senting its overload compared to neighbors. Then, it

will search among its neighbors which are most likely

to beneﬁt from receiving additional territory (e.g. de-

pending on their own load, territory size, number of

neighbors) and rank them by load score to give. It

will then choose among its cells which are the most

interesting for that neighbor and distribute them until

it reached the load score previously set, switching to a

new neighbor if necessary. As in (Miller and Luding,

2004), the algorithm should make sure to keep terri-

tories in one piece and to minimize their perimeters.

4 CASE STUDY

In this section, we present statistics from simulations

performed on our ongoing implementation. We ob-

serve the behavior of synchronizations in our imple-

mentation to choose the most suitable granularity of

space distribution among worlds. We also illustrate

the interest of anticipation in terms of resistance to

frame-rate drop-downs.

The implementation uses open-source software

(the Bullet Physics engine v2.79 and the Ogre 3D

engine v1.7). At the time of writing this paper, dis-

tributed CD was implemented but CS had not yet been

adapted to manage foreign bodies’ constraints within

a world. We did not seek to evaluate raw performance

as our implementation conﬂicts with many of the op-

timizations present in the engine we used. We focus

only on the feasibility of a distributed physics pipeline

and on reducing the amount of synchronizations to an

acceptable level.

4.1 Distribution of Synchronizations

The following experiment was performed on a sys-

tem with two Intel Xeon X5680 processors, for a total

of 12 CPUs. The system has 48GB RAM, and runs

Linux 3.2. We wrote a parallel shared-memory im-

plementation, each world running in a thread of the

100

1000

500

Rigid bodies

Worlds per

group size

5-8

2-4

9-11

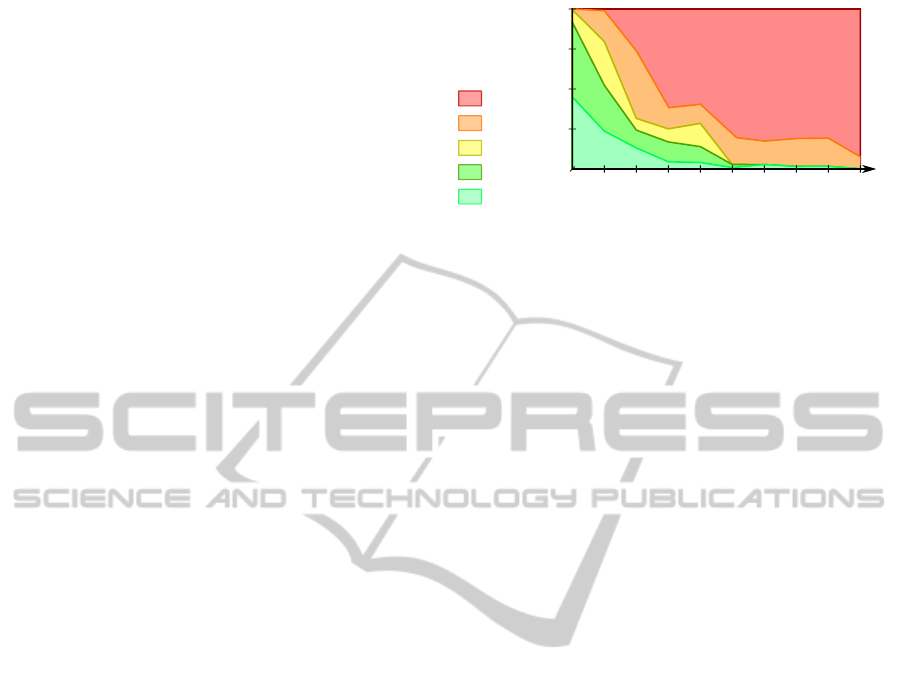
Figure 6: Evolution of the number of worlds per sizes of

synchronization groups, depending on the density of the

simulation.

same process. This choice was made as no PC cluster

with more cores was available.

We explored the potential for distribution with our

current deﬁnition of territories and borders. To do so,

we ran a simulation with twelve worlds and a growing

number of bodies (hence a growing density), homo-

geneously and randomly distributed in the space. The

space was 24000 km

, and the simulated bodies were

cubes of 100 cm

. We ran each simulation ﬁve times

for ten seconds (at 60 FPS) and aggregated results for

each time steps.

Although it may seem a school case for traditional

CD algorithms, the homogeneity of the positioning

means that it is impossible for worlds to map their

territories to “collision hot spots”. Because there are

very few worlds for such a large space, borders be-

tween worlds are very large and inevitably overlapped

by at least one cube.

Figure 6 shows worlds classiﬁed by the size of

their synchronization group, on average. It is obvi-

ous that such a coarse granularity has no chance of

bringing performance improvements over parallel ap-

proaches: it would need to scale for thousands of bod-

ies rather than a few hundreds.

We classiﬁed groups for better readability, de-

pending on what kind of scalability groups of their

size would obtain with state-of-the-art algorithms

from the CD litterature. For instance, groups below

four worlds would obtain full scalability while those

above eight would start being limited. The idea is to

visualize the groups that have a critical size and that

will decrease the overall scalability of the simulation.

Our second experiment seeked to evaluate the im-

provements we would obtain from using more worlds.

We ran on the same system a similar simulation with

ﬁve hundred bodies (where the previous simulation

was almost fully synchronized), and a varying number

of worlds. As Figure 7 suggests, synchronizations be-

come rarer with as few as ﬁve to ten bodies per world.

From this perspective, we recommand that dis-

tributed collision handling be run on many-core ar-

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

344

Worlds

Worlds per

group size

564812 20 32 40

9-12

4-8

13-20

21-36

37+

1-4

Figure 7: Evolution of the number of worlds in each

connected-group size class, depending on the number of

cores.

chitectures with very ﬁne-grained distribution of the

space. Miller and Luding used such a small granu-

larity while Li et al. chose to simulate bodies directly

rather than territories regrouping few bodies. Besides,

there are incentives for chosing simulation islands as

a unit of task decomposition, for the CS stage of the

collision handling pipeline.

Current parallel CD algorithms make use of

GPUs, which are a form of many-core architecture,

but we argue that current state of GPGPU languages

is limiting potential for anticipation and asynchronous

computing because it allows the use of GPUs only as

passive devices which need a CPU to send data and

launch kernels. However, we may see the emergence

of new classes of distributed algorithms, similar or not

to SODA, when GPGPU languages and frameworks

start offering more ﬂexibility.

4.2 Anticipation Beneﬁts

We evaluate the beneﬁts of anticipations in SODA

with a function taking two parameters: a percentage

of overload for a process, and the size of a buffer in

which anticipated entries are stored. It should inform

on the number of simulation steps that can be com-

puted and used (including those in the buffer) before

a process will start being too late to cope with the ren-

dering frame rate.

In implementations, such a function could be used

to evaluate the cost-efﬁciency of anticipation (com-

paring the size requirement of a buffer and its ability

to provide resilience to frame-rate drop-downs), or the

emergency of load balancing for discrete CD systems.

Indeed, load balancing can be delayed when the addi-

tional workload is limited and does not represent a

high risk of lateness for a given process.

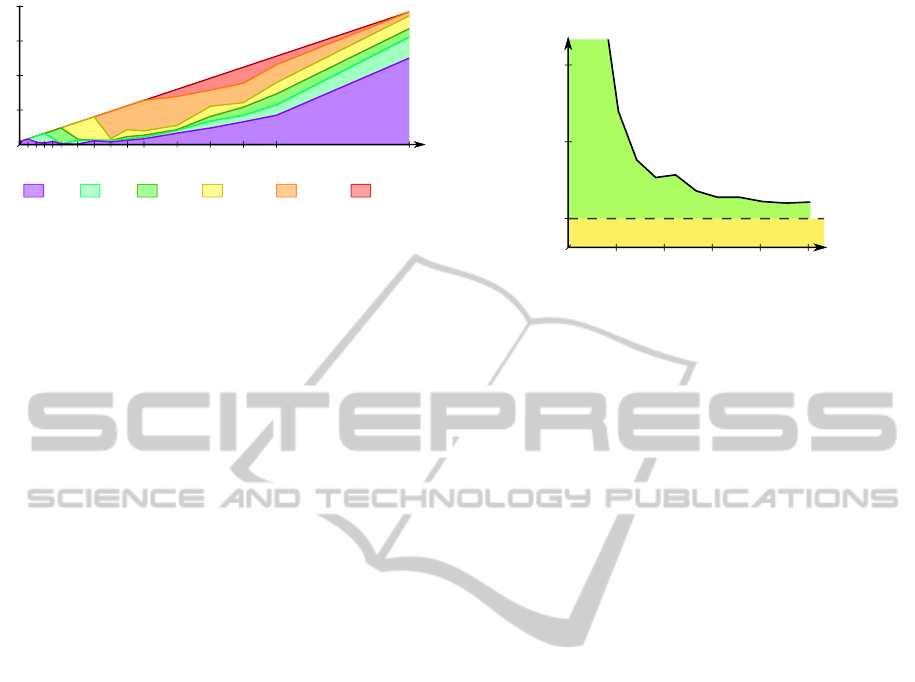
We designed an experimental case study, running

at 60 FPS with a single world running on a Intel Xeon

W3540 CPU (2.93GHz). We simulated 40 cubes per-

fectly overlapping, and put them back to their orig-

inal position after each simulation step, so that they

144

0 30 60 90 120 150

Extra

load

Steps computed

before ﬁrst delay

Buﬀer size beneﬁts

Anticipation

beneﬁts

Figure 8: Example of anticipation beneﬁts function for a

world run on a Xeon W3540 with a buffer of 48 anticipated

entries.

would keep overlapping (though we did not reset ac-

celeration). We used a 2-body broad-phase algorithm,

which has exponential complexity. Hence, we eval-

uated increases in work load in terms of number of

checks to perform when adding bodies. This num-

ber of cubes was enough for the collision handling

pipeline of our prototype to ﬁll the transform buffer,

yet adding more cubes would cause the world to miss

the 60 FPS target.

After a warm-up phase of one second to ﬁll

buffers, we added enough cubes to reach a wanted

threshold of additional cost, and calculated the time it

would take for the world not to be able to provide an

entry on due time to the rendering process. Results are

shown in Figure 8 and indicate that there is a clear in-

terest to allow anticipation rather than to simpler cou-

pling of collision handling and rendering. Even with

a 150% load increase, the world had up to a second

(sixty steps) to react and trigger load balancing.

In practice, we expect that load balancing algo-

rithms with direct access to anticipation beneﬁts func-

tions for a variety of buffer sizes would be able to

adapt the aggressiveness and granularity of their load

balancing using the number of anticipated entries they

store in their buffers. In a distributed context where

processors can be added to match the computational

needs of an application, resilience to frame-rate drop-

downs is a desired property that may let processes

perform load balancing only when it is necessary and

focus on useful computation instead.

5 CONCLUSIONS

In this paper, we have presented SODA, the ﬁrst col-

lision handling model designed for low-latency dis-

tributed systems. SODA is designed for high scal-

ability on systems with tens to hundreds of CPUs,

SODA:AScalability-OrientedDistributed&AnticipativeModelforCollisionDetectioninPhysically-basedSimulations

345

using decentralization and anticipation to reach this

goal. We showed how collision handling can be per-

formed in a distributed way among several processes,

without constant clock synchronization between pro-

cesses. We proposed a novel rollback algorithm to

improve the efﬁciency of anticipative computation.

We showed that there is potential for load bal-

ancing in SODA. We showed the limitations of our

broad-grained approach, with synchronizations still

too frequent for proper distributed computation with-

out a signiﬁcant number of concurrent worlds, which

we will have to address by ﬁnding ﬁner-grained task

decompositions. Finally, we evaluated in a case study

the expected ability of anticipation to mitigate frame-

rate drop-downs that may harm user experience.

In the future, we intend to develop speciﬁc con-

straint solvers for distributed contexts, in order to im-

prove rollback and to solve constraints in parallel with

least communication between two cores. We also

want to integrate the motion of objects into load bal-

ancing decisions, and to use the static environment for

initial territory setup. Finally, we want to explore the

efﬁciency of SODA for speciﬁc applications such as

indoor crowd simulation or complex factory environ-

ment simulations, with predictable ﬂows of motions.

ACKNOWLEDGEMENTS

We address our thanks to Bruno Arnaldi and the

anonymous reviewers for their feedback, Alexan-

dra Covaci for her help in processing experiments

data and Loeiz Glondu for our insightful discussions

on linear constraint solvers. This work was partly

supported by the French Research National Agency

project named Corvette (ANR-10-CONTINT-CORD-

012).

REFERENCES

Asanovic, K., Bodik, R., Catanzaro, B. C., Gebis, J. J.,

Husbands, P., Keutzer, K., Patterson, D. A., Plishker,

W. L., Shalf, J., Williams, S. W., and Yelick, K. A.

(2006). The landscape of parallel computing research:

A view from berkeley. Technical Report UCB/EECS-

2006-183, EECS University of California, Berkeley.

Chen, T. C. L. and Verbrugge, C. (2010). A protocol for

distributed collision detection. In Proceedings of the

9th Annual Workshop on Network and Systems Sup-

port for Games, NetGames ’10, pages 6:1–6:6. IEEE

Press.

Cosenza, B. (2010). Efﬁcient distributed load balancing for

parallel algorithms. PhD thesis, Universita degli studi

di Salerno.

Ericson, C. (2005). Real-time Collision Detection. Morgan

Kaufmann.

Fujimoto, R. (1999). Parallel and distributed simulation.

In Simulation Conference Proceedings, 1999 Winter,

volume 1, pages 122 –131 vol.1.

Hermann, E., Rafﬁn, B., and Faure, F. (2009). Interac-

tive physical simulation on multicore architectures. In

EGPGV, pages 1–8. Eurographics Association.

Hermann, E., Rafﬁn, B., Faure, F., Gautier, T., and Allard,

J. (2010). Multi-GPU and multi-CPU parallelization

for interactive physics simulations. Europar.

Kim, D., Heo, J.-P., and eui Yoon, S. (2008). Pccd: Parallel

continuous collision detection. Technical report, Dept.

of CS, KAIST.

Kim, D., Heo, J.-P., Huh, J., Kim, J., and Yoon, S.-E.

(2009). HPCCD: Hybrid parallel continuous collision

detection using CPUs and GPUs. Comput. Graph. Fo-

rum, 28(7):1791–1800.

Le Grand, S. (2007). Broad-phase collision detection with

cuda. GPU Gems 3 - Nvidia Corporation.

Li, R., Jiang, H., Su, H.-C., Zhang, B., and Jenness, J.

(2007). Speculative and distributed simulation of

many-particle collision systems. In 13th International

Conference on Parallel and Distributed Systems, IC-

PADS ’07, pages 1–8.

Lin, M. C. and Gottschalk, S. (1998). Collision detection

between geometric models: a survey. In 8th IMA Con-

ference on the Mathematics of Surfaces (IMA-98), vol-

ume VIII of Mathematics of Surfaces, pages 37–56.

Miller, S. and Luding, S. (2004). Event-driven molecular

dynamics in parallel. J. Comput. Phys., 193(1):306–

316.

Morgan, G. and Storey, K. (2005). Scalable collision de-

tection for massively multiplayer online games. In

Proceedings of the 19th International Conference on

Advanced Information Networking and Applications -

Volume 1, AINA ’05, pages 873–878. IEEE Computer

Society.

Pabst, S., Koch, A., and Straβer, W. (2010). Fast and

scalable cpu/gpu collision detection for rigid and de-

formable surfaces. In Comput. Graph. Forum, vol-

ume 29, pages 1605–1612.

Rafﬁn, B. and Soares, L. (2006). Pc clusters for virtual real-

ity. In Proceedings of the IEEE conference on Virtual

Reality, VR ’06, pages 215–222.

Tang, M., Manocha, D., and Tong, R. (2009). Multi-core

collision detection between deformable models. In

Symposium on Solid and Physical Modeling, pages

355–360.

Thomaszewski, B., Pabst, S., and Blochinger, W. (2008).

Parallel techniques for physically based simulation

on multi-core processor architectures. Computers &

Graphics, 32(1):25–40.

Tonge, R., Benevolenski, F., and Voroshilov, A. (2012).

Mass splitting for jitter-free parallel rigid body sim-

ulation. ACM Trans. Graph., 31(4):105:1–105:8.

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

346