Automated Classiﬁcation of Therapeutic Face Exercises using the Kinect

Cornelia Lanz

, Birant Sibel Olgay

, Joachim Denzler

and Horst-Michael Gross

Neuroinformatics and Cognitive Robotics Lab, Ilmenau University of Technology, Ilmenau, Germany

Computer Vision Group, Friedrich Schiller University Jena, Jena, Germany

Keywords:

Facial Expressions, Curvature Analysis, Point Signatures, Line Proﬁles, Therapeutic Exercises.

Abstract:

In this work, we propose an approach for the unexplored topic of therapeutic facial exercise recognition us-

ing depth images. In cooperation with speech therapists, we determined nine exercises that are beneﬁcial for

therapy of patients suffering from dysfunction of facial movements. Our approach employs 2.5D images and

3D point clouds, which were recorded using Microsoft’s Kinect. Extracted features comprise the curvature

of the face surface and characteristic proﬁles that are derived using distinctive landmarks. We evaluate the

discriminative power and the robustness of the features with respect to the above-mentioned application sce-

nario. Using manually located face regions for feature extraction, we achieve an average recognition accuracy

of about 91% for the nine facial exercises. However in a real-world scenario manual localization of regions

for feature extraction is not feasible. Therefore, we additionally examine the robustness of the features and

show, that they are beneﬁcial for a real-world, fully automated scenario as well.

1 INTRODUCTION

Facial expressions are key to interpersonal commu-

nication. Diseases like stroke or mechanical injury

of the facial nerve can lead to a dysfunction of fa-

cial movements. These impairments of facial expres-

sions may have various consequences that can con-

strain daily life and can lead to social isolation. Exam-

ples for these consequences are eating difﬁculties, im-

paired appearance of the face, and misunderstandings

in face-to-face communications due to ambiguous fa-

cial expressions. Similar to rehabilitation exercises

that help to regain body functions, there are exercises

for the recovery of facial expressions. Besides prac-

tising under supervision of a speech therapist, patients

additionally have to conduct unattended exercises on

their own. However, the incorrect conduction of exer-

cises can impede the training success or even lead to

further impairment. An accompanying training plat-

form could enrich unsupervised training exercises by

tutorial, feedback and documentation functions. Tu-

torial functions can support correct exercise conduc-

tion by providing text and video instructions. A feed-

back function could give advice regarding mistakes

or inaccuracies during training. The documentation

in form of videos or feedback enables the therapist to

review the past unsupervised training units, if neces-

sary. The conception and implementation of such a

training platform is a challenging and complex task

that comprises several subtasks. In this work we will

focus on one subtask, that is, the evaluation of fea-

tures. However, to enable a better understandig of the

context of our work, we give a short overview of the

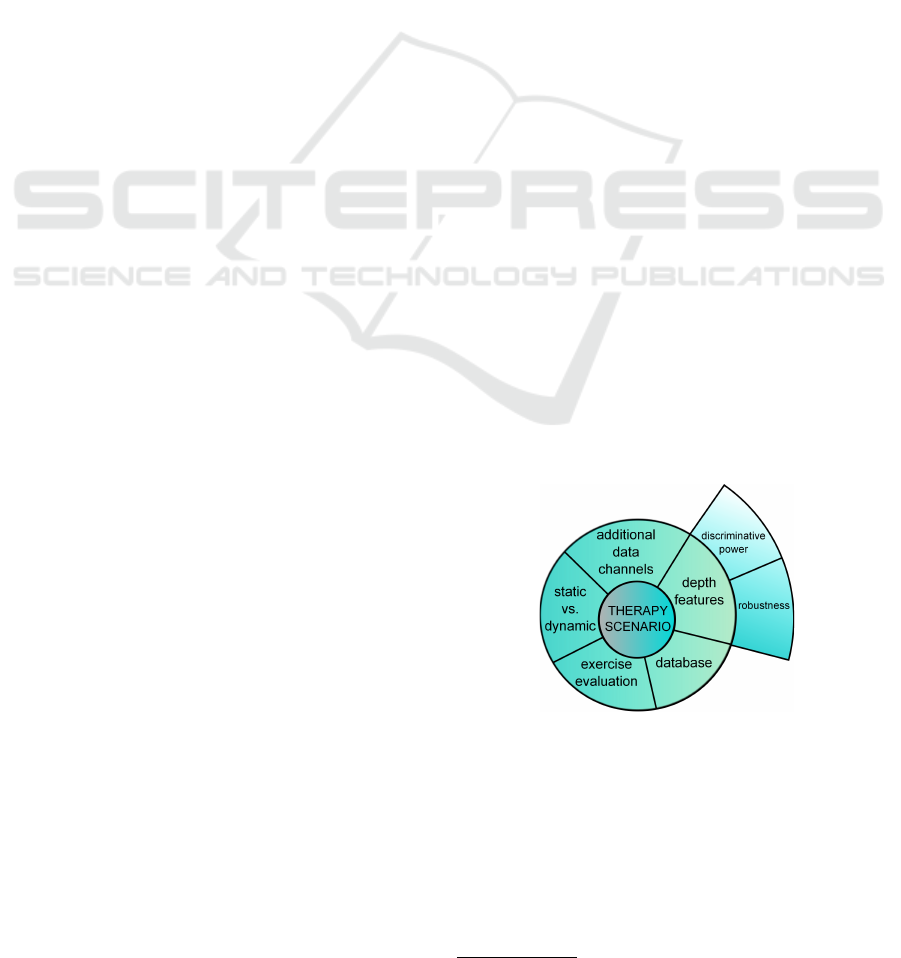
remaining subtasks. Figure 1 presents ﬁve of the in-

volved subtasks, which will be discussed in the fol-

lowing.

Figure 1: Different subtasks of the conception and imple-

mentation of an automated therapeutic exercise platform.

Facial movements cause changes of the face sur-

face, which can be captured by depth image sen-

sors like Microsoft’s Kinect

or Time-of-ﬂight Cam-

eras

. The extraction of depth features allows to

examine the face surface, independently from skin

colour and lighting conditions. Although there exist

other systems that are capable of recording depth data

http://www.xbox.com/en-US/kinect

http://www.pmdtec.com/

http://www.mesa-imaging.ch/

556

Lanz C., Olgay B., Denzler J. and Gross H..

Automated Classiﬁcation of Therapeutic Face Exercises using the Kinect.

DOI: 10.5220/0004294005560565

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 556-565

ISBN: 978-989-8565-47-1

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

with much higher depth resolution than the Kinect

(e.g. (Grosse et al., 2011)), we decided to use this sen-

sor because of its moderate price. This makes such

an application suitable for widespread use in low-cost

training platforms. Furthermore, the Kinect allows to

capture additional data channels such as intensity

images in parallel to depth images. These might be

helpful if depth information is not suitable to describe

certain facial movements. For example, it can hardly

be determined whether the eyes are closed by solely

employing depth information.

The nine therapeutic face exercises that we focus

on in this paper are rather static. The pace of the ex-

ercise conduction from neutral face to ﬁnal state, e.g.

both cheeks puffed, is not important. It is more rel-

evant that the exercises ﬁnal states are retained for

some seconds. Nevertheless, it is likely that additional

information, obtained by examining the dynamics of

an exercise instead of single static snapshots, may

contain valuable information. Additionally, it is pos-

sible to reduce the amount of noise in the data by

smoothing over time.

The evaluation of the exercises, which is essen-

tial for a feedback functionality, is a complex task.

Besides the choice of appropriate technical tools, it is

necessary to deﬁne, in which cases an exercise is per-

formed correctly and in which it is not. Additionally,

we need to assess how feedback should be communi-

cated in order to be most beneﬁcial for a patient.

Furthermore, it is necessary to collect a database

of training and test images that contain the exercises

performed by healthy people as well as the exercise

conduction by people with dysfunction of facial ex-

pression abilities. In our experiments, nine therapeu-

tic facial exercises are employed that have been de-

ﬁned in cooperation with speech therapists. We only

employ training and test data recorded from exercises

of healthy persons. We omit data recorded from per-

sons with dysfunction of facial expressions, as we ex-

pect their ground-truth to be ill-deﬁned. This is due

to the circumstance, that incorrect conduction of an

exercise may resemble other exercises, as shown in

Figure 2.

Since each of the above-mentioned subtasks con-

sists of diverse aspects, we focus on the extraction and

evaluation of depth features in this publication. Our

depth features are extracted from 2.5D images and 3D

point clouds recorded by the Kinect Sensor. We refer

to 2.5D images as 2D images that contain the object-

to-camera distance instead of the object’s intensity

value. We analyse the facial surface by extraction of

curvature information and surface proﬁles. Surface

proﬁles comprise line proﬁles and point signatures.

Line proﬁles are based on paths that connect two land-

mark points, whereas point signatures are based on

radial paths around single landmark points.

We examine the features’ discriminative power

with respect to the classiﬁcation of nine therapeutic

exercises and their robustness regarding varying fea-

ture extraction regions. In the targeted real-time sce-

nario regions and points for feature extraction need to

be determined automatically. We expect that this step

leads to variations from manually located face regions

and landmarks. Therefore it is necessary that the fea-

tures are robust against these deviations.

Figure 2: Patient with facial paresis on his right side. Left

image: The exercise right cheek puffed is conducted cor-

rectly because the bulge of the cheek is a passive process as

reaction of a higher air pressure inside the mouth and a con-

traction of the buccinator on the left facial side. Right im-

age: The exercise left cheek puffed is conducted incorrectly.

The lack of contradiction in the right buccinator leads to the

bulge of the right cheek.

2 RELATED WORK

Automated recognition of therapeutic face excercises

is an unexplored research ﬁeld. In practice, there are

already tools that support the patient with regard to

exercising that is not supervised by a therapist. These

tools are videos and programs that give instructions

to the patient, with respect to correct exercise con-

duction (LogoVid

), and, to some extent, allow for

a documentation of exercise frequency and success

(CoMuZu

). The documentation, however, is done by

the patient himself, which is often impractical or even

questionable. At the moment, there are no commer-

cial solutions available that automatically recognize a

performed therapeutic exercise.

(Nakamura et al., 2003) evaluated the success

of facial exercises to prevent synkinesis after facial

paresis. Synkinesis is an involuntary associated facial

movement such as eye closure during smiling. They

manually measure the eye opening width by using an

image editing software. (Gebhard et al., 2000) pre-

sented a system for the diagnosis support of patients

http://www.comuzu.de

http://www.logomedien.de/html/logovid7a.html

AutomatedClassificationofTherapeuticFaceExercisesusingtheKinect

557

with facial paresis using 2D colour images. There-

fore, they analysed facial asymmetries in the eyes,

nose and mouth regions.

At present, there are no publications known to us

that focus on the automated recognition of therapeu-

tic facial exercises using depth information. Never-

theless, we can utilize approaches from works on face

detection, as well as person and emotion recognition.

(Colombo et al., 2006) use curvature of the surface of

a 2.5D image to detect salient face features like eyes

and nose. A triplet consisting of a candidate nose and

two candidate eyes is processed by a classiﬁer that is

trained to discriminate between faces and non-faces.

Based on curvature information estimated on a 3D tri-

angle mesh model, (Wang et al., 2006) classify 3D

faces according to the emotional state that they repre-

sent.

Point signatures were developed by (Chua and

Jarvis, 1997) as an approach for 3D object recogni-

tion. They presented an enhanced algorithm for face

recognition based on point signatures in (Chua et al.,

2000). (Wang et al., 2002) extracted point signatures

in 2.5D images and Gabor ﬁlter responses in gray-

level images and employed their combination for face

recognition.

In this work we orient on the method of (Wang

et al., 2006) to create histograms of curvature types.

We utilize the face recognition algorithm from (Chua

et al., 2000) for the classiﬁcation of our nine thera-

peutic exercises and supplement it with a similar ap-

proach that employs line proﬁles instead of radial pro-

ﬁles. In contrast to (Wang et al., 2006), where manu-

ally placed landmarks are used, we additionally eval-

uate our results with automatically located landmark

positions.

3 METHOD

In the following, we brieﬂy review the determination

of surface curvature (section 3.1) as far as it is neces-

sary to understand the basic principles of our curva-

ture feature types (section 3.2). For detailed informa-

tion we refer to (Besl and Jain, 1986). In sections 3.3

and 3.4 the extraction of line proﬁles and point signa-

tures is presented. In the last section, we focus on the

automation of the feature extraction process.

3.1 Curvature Analysis

Our aim is the classiﬁcation of faces according to

the therapeutic exercises a patient performs. Facial

movement leads to a change of the face surface. We

analyse the surface by extracting curvature informa-

tion from 2.5D range images and 3D point clouds.

The parametric form of a surface in 3D is s(u, v) =

[x(u, v) y(u, v) z(u, v)]

, with u and v denoting the axes

of the parameter plane (Figure 3). On the basis of this

function, we can determine the ﬁrst and the second

fundamental forms, which uniquely characterize and

quantify general smooth shapes. The elements of the

ﬁrst fundamental form I are:

I =



· s



. (1)

The subscripts denote partial differentation. The ele-

ments of the second fundamental form J are:

J =



· n s

· n

· n s

· n



, (2)

with n being the unity normal vector of the tangent

plane in the point with parameters (u, v). Although

both fundamental forms are a unique representation

of the surface, more common for surface character-

ization are combinations of both, because they allow

for an intuitive interpretation. Using I and J, the shape

operator matrix W can be computed by:

W = I

−1

· J. (3)

The mean curvature H gives information about the di-

rection of the curvature (convex, concave) and is de-

termined by:

H =

tr [W] , (4)

with tr [W] being the trace of the shape operator W.

The Gaussian curvature K contains the information

whether curvatures that are orthogonal to each other

point in the same or in different directions (Figure 4).

It is computed as follows:

K = det [W]. (5)

Opposed to the general parametric representation, the

parametrization of a 2.5D range image takes a very

simple form s(u, v) = [u v z(u, v)]

. Because a 2.5D

image is spanned by two axes that generate a discrete

(pixel) grid the derivation of s with respect to u and

v is simpliﬁed and results in s

= [1 0 z

]

and s

[0 1 z

]

. Therefore, for the computation of H and K

only the partial derivatives of z are relevant:

H =

+ z

− 2z

(1 + z

+ z

)

, (6)

K =

− z

(1 + z

+ z

)

. (7)

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

558

uv - Parameter Plane

Surface in R³

s(u,v)

(u,v)

Figure 3: Surface in 3D with the corresponding parameter

plane (image according to (Besl and Jain, 1986)).

Figure 4: Two surfaces with orthogonal maximum and min-

imum curvatures that point in different (upper surface: hy-

perbolic convex) and in the same directions (lower surface:

elliptic convex).

3.2 Extraction of Curvature

Information

Prior to feature extraction, we smooth the face sur-

face using an average ﬁlter. On a subset of the data,

we performed tests with different ﬁlter sizes and ﬁl-

ter parameters, which showed that adequate low-pass

ﬁltering has strong impact on the success of classi-

ﬁcation. For example, Gaussian ﬁltering was tested

but resulted in lower classiﬁcation results compared

to average ﬁltering.

We extract the mean and Gaussian curvature for

each pixel, respectively 3D-point, to obtain informa-

tion about the facial surface. This results in around

2 × 8000 to 2 × 13000 values per face, depending on

the face-to-camera distance. In order to reduce the

dimensionality of the feature space, we summarize

the curvature values with a histogram (Wang et al.,

2006). To maintain spatial information, we deﬁne

four regions (A-D) from which histograms are ex-

tracted (Figure 5). Each histogram is weighted with

the number of pixels of the region described by it.

The selected cheek regions are axially symmetric, due

to the fact that some of the therapeutic exercises are

asymmetric and each face side contains valuable in-

formation. Two additional regions, in which high fa-

cial surface variation among all exercises is visible,

were determined. Further reﬁnement of the regions

was omited to maintain a certain robustness in case of

automatically determined regions.

The curvature type histogram feature is obtained

by extraction of mean curvature H and Gaussian cur-

vature K for every 2.5D pixel, respectively 3D point

according to equations (4)-(7). In the next step, both

values are combined to discrete curvature types as

Figure 5: Regions A-D are employed for curvature fea-

ture extraction. Region borders are derived from landmark

points 1-5. The determination of the landmark points is ex-

plained in sections 3.5 and 4.1.

shown in Table 1 (Colombo et al., 2006). Subse-

quently, the discrete curvature types of each region

are summarized with histograms. The concatenation

of these histograms forms the feature vectors that are

subjected to the classiﬁcation process. For each image

a 32 dimensional feature vector is extracted (8 curva-

ture type histogram bins per region).

3.3 Extraction of Line Proﬁles

Although curvatures are extracted from each pixel,

their combination in a histogram blots out some of

the local information. Line proﬁles, in contrast, con-

tain local information by describing paths along the

face surface. Instead of using 2.5D images, line pro-

ﬁles are extracted from a point cloud, which lies in

a three-dimensional space. Each of the three dimen-

sions is expressed in metre. For a 2.5D image the two

dimensions are given in pixel units. However, the real

world distance that is described by the difference of

one pixel depends on the person-to-camera distance.

The smaller the distance of an object to the camera is,

the more pixels does this object cover on a 2.5D im-

age. As a result, comparison of different line proﬁles

is more difﬁcult, when using 2.5D images.

In total, we extract nine line proﬁles from the 3D

point cloud of the face. Every line proﬁle connects

two deﬁned landmark points. Figure 6 shows the

paths of the proﬁle lines. Seven proﬁles start at the

nose tip, connecting it in radial direction to silhouette

points. Two line proﬁles are horizontally located and

link two silhouette points.

The paths over the face consist of N equidistant

points p

(x, y, z), with n = 1...N. Nearest-neighbour

interpolation is employed in order to calculate miss-

ing points. The L2-norm of the position vectors of

every 3D point p

already creates a distinctive curve

as can be seen in Figure 7. However, in order to

achieve invariance with respect to the viewpoint (i.e.,

translation and rotation operations of the facial point

cloud), relative central differences between the 3D

points are calculated (left image of Figure 8). The im-

ages show, that the curves consist of 70 samples. This

AutomatedClassificationofTherapeuticFaceExercisesusingtheKinect

559

Table 1: Curvature type deﬁnition using mean and Gaussian curvature (H, K).

K < 0 K = 0 K > 0

H < 0 hyperbolic concave cylindric concave elliptic concave

H = 0 hyperbolic symmetric planar impossible

H > 0 hyperbolic convex cylindric convex elliptic convex

Figure 6: 3D face with marked paths of the nine line pro-

ﬁles.

0 10 20 30 40 50 60 70

0.66

0.67

0.68

0.69

0.7

0.71

0.72

0.73

0.74

Original line profile

point index

vector lengths (in metre)

Figure 7: Line proﬁle from nose tip to the point of the chin

for the exercise A-shape.The curve shows the length (in me-

tre) of the position vector of each point p

. The opening of

the mouth, resulting in higher values, in the middle of the

curve and the chin shape on the right are visible.

0 20 40 60 80

x 10

−3

Distance line profile

point index

central difference (in metre)

0 5 10 15

0.005

0.01

0.015

Reconstructed distance line profile

point index

central difference (in metre)

Figure 8: Left: Distance line proﬁle. Right: The recon-

structed line proﬁle using the ﬁrst 12 dct-coefﬁcients.

ref

eye

Figure 9: Landmark points and line segments that are em-

ployed for the extraction of point signatures.

value may vary because the size of the head (subject-

speciﬁc) or the length of the curve (exercise-speciﬁc)

may change. To get an identical size of the curve

for every subject and every exercise and to reduce

the amount of feature dimensions we conduct a dis-

crete cosine transform (Salomon, 2004) on the curves

and build our feature vector using the ﬁrst 12 dct-

coefﬁcients. The right image of Figure 8 shows, that

the inverse discrete cosine transform with 12 coefﬁ-

cients yields a reasonable reconstruction of the origi-

nal curve. We derived the line proﬁles from the point

signature approach presented in the following section.

3.4 Extraction of Point Signatures

Similar to line proﬁles, point signatures are paths on a

surface (Chua and Jarvis, 1997). Instead of connect-

ing two landmark points the curve runs radial around

a distinctive point p

of a 3D point cloud. As can be

seen in Figure 9, in our approach the point p

is lo-

cated on the tip of the nose. In order to obtain the

point signature, a sphere is centered into the point p

of the 3D point cloud. The intersection of the sphere

with the facial points forms a curve Q in the three-

dimensional space (left image of Figure 10). The

depth information of these intersection points, com-

bined with the value of the sphere radius, contains

characteristic and unique information about the depth

value distribution in the surrounding area of the point

. However, taking the absolute depth values of this

intersection points is not reasonable (as already dis-

cussed for the line proﬁles in section 3.3) because they

are not independent with respect to translation and ro-

tation of the head. As a result, we create a reference

curve Q

that can be employed to calculate relative

depth information. To obtain this curve, we ﬁt a plane

P through the set of intersection points. The plane

is determined with regression analysis by a singular

value decomposition that gives the surface normal of

the plane. The plane is now shifted along its normal

vector into the point p

. This results in a new plane

called P

(right image of Figure 10). In the next step

the curve Q is projected onto P

building a new curve

. Now the curve Q

is sampled around the approxi-

mated surface normal at p

with a rotation angle of 15

degrees. For each sampled point in Q

the distance to

its corresponding point in Q is collected. The starting

position for the distance sampling needs to be equal

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

560

between the different images to obtain curves that are

comparable. Therefore, we deﬁne a starting position,

which is determined by a reference point p

re f

. The

reference point is located on the chin as marked in

Figure 9. The sphere radius length has to be deter-

mined such that the arising path does not protrude be-

yond the surface of the face and no background points

are sampled. The length of the radius is computed

from the eye distance d

eye

, multiplied by a factor f .

The eye distance is estimated from the distance be-

tween the mean positions of each eye. Mean posi-

tions are obtained by the landmark positions of each

eye (Figure 9). We use the following values for the

empirically determined factor f to extract ﬁve differ-

ent point signatures: 0.4, 0.5, 0.7, 0.8 and 1.0.

Sampling of the radial curve with a ﬁxed interval

of 15 degrees generates 24 values per point signature.

The more point signatures are extracted, the more pre-

cisely the surface of the face can be described. How-

ever, a high amount of point signatures leads to a

high-dimensional feature space. We reduce the di-

mension of the feature vector by applying discrete co-

sine transform on each point signature as shown in

section 3.3. Again the ﬁrst twelve coefﬁcients are re-

tained.

Figure 10: Left image: Intersection curve Q of the sphere

with the 3D point cloud. Right image: The planes P (red)

and P

(magenta). The projected curve Q

is marked on P

3.5 Automation of the Feature

Extraction Process

The features presented above have in common that

certain facial areas need to be determined for extrac-

tion. These can be landmark positions or regions de-

rived from these landmark positions. Manual determi-

nation of the landmarks and regions is not feasible in a

real-world application. Thus, they have to be detected

automatically, which may lead to less accuracte local-

izations. We use two different approaches to test the

robustness of the presented features with respect to

these deviations. The ﬁrst approach is the application

of Active Appearance Models (AAMs) for landmark

detection. The second approach is a threshold-based

localization of the nose tip position using curvature

analysis.

AAMs are mainly applied in the ﬁeld of fa-

cial expression recognition on 2D gray-value im-

ages (Cootes et al., 2001). On the basis of several

training images a combined mean texture and shape

model is derived. The ﬁtting of this mean model to

a new and unknown face is improved by determina-

tion of a coarse initialization position. We use the

Viola and Jones face detector to ﬁnd an initial lo-

calization (Viola and Jones, 2004). In the next step

the AAM adapts itself to the new face by minimiz-

ing the error between the model intensities and the

image intensities. The parameters that describe the

ﬁtted model are usually subjected to classiﬁcation of

facial expressions. In constrast to this, the AAM can

be used for the mere detection of landmarks without

further consideration of the model parameters (Haase

and Denzler, 2011). In this paper we focus on the

application of AAMs for landmark detection. The

AAM is ﬁtted on the 2D intensity images and we need

to transform these landmark positions to positions in

depth images. Therefore intrinsic and extrinsic cam-

era parameters were determined by camera calibra-

tion (Hartley and Zisserman, 2000). They can be

employed to align the 2.5D images with their corre-

sponding intensity images. As a result, correspond-

ing points have the same position in the images of

both channels and the labeled landmark positions can

be accordingly transferred. Additionally, these cam-

era parameters can be used to transform the points of

the 2.5D image to a discrete 3D point cloud (Hartley

and Zisserman, 2000).

Landmark detection by AAMs is complemented

by the detection of the nose tip using curvature anal-

ysis. Again, a coarse initalization is necessary to con-

strain the search space, e.g., by the Viola and Jones

face detector. Mean and Gaussian curvature is calcu-

lated for each 3D point that belongs to the delimited

search space. The largest region that fullﬁlls certain

thresholds for both curvature measures is deﬁned as

the nose region. Inside the nose region we search for

the point that has the lowest distance to the camera.

We evaluated this approach on 1485 images and 13

persons by comparing the manually labeled nose tip

to the nose tip detected by curvature analysis. For

94% of the images the distance in x-and y-direction

is smaller than 0.95cm. The nose tip detection algo-

rithm works, even if the head is slightly rotated. An

example can be seen in Figure 11. However large

rotations should be avoided in the whole application

scenario because therapeutic exercises can not be rec-

ognized and evaluated correctly if important regions

of the face are occluded.

AutomatedClassificationofTherapeuticFaceExercisesusingtheKinect

561

Figure 11: Left: Gray-value image. Center: Depth image

with nose tip position marked. Nose tip position was deter-

mined by curvature analysis. Right: Regions that fulﬁll the

necessary thresholds for Gaussian and mean curvature. The

largest region belongs to the region of the nose.

4 EXPERIMENTS

In the ﬁrst section of the experimental part, we focus

on the dataset and the exercises that are used for our

experiments. The evaluation of the features discrimi-

native power with respect to the classiﬁcation of ther-

apeutic exercises is presented in section 4.2. Results

from experiments that test the robustness of the fea-

tures related to variations of region borders are given

in the last section.

4.1 Exercises and Dataset

In cooperation with speech therapists, we selected a

set of nine therapeutic face exercises by certain crite-

rions. The exercises should train the lips, the cheeks

and the tongue and should be beneﬁcial for various

types of facial muscle dysfunctions, e.g. paresis of

muscles or muscle imbalance. Furthermore, the se-

lected exercises should be easy to practice and should

build a set of sub-exercises that can be combined to

more complex dynamic exercise units, e.g. by alter-

nating between them. The exercises have to be per-

formed in an exaggerated manner, to enable a max-

imum training effect, and have to be retained for

around two or three seconds. The speed of the per-

formance is not important. Although some of these

are vocal exercises, it is not necessary to vocalize a

continuous sound while performing the shape. Im-

ages that visualize the exercise conduction are shown

in Figure 12.

Due to the lack of a public database that shows

the performance of therapeutic exercises, we recorded

a dataset, which contains eleven persons, who con-

duct the nine exercises. For each exercise, there are

around seven images, showing different states of ex-

ercise conduction. This amounts to a total size of 696

images in the dataset. Some parts of the scene that

is captured by the Kinect may be shadowed, if they

are seen by the depth camera but are not illuminated

by the infrared projector. This leads to invalid values

in the 2.5D image (Khoshelham, 2011). These values

Figure 12: Exercises that have been selected in cooperation

with speech therapists (from left to right and top to bottom):

pursed lips, taut lips, A-shape, I-shape, cheek poking (right/

left side), cheeks puffed (both/ right/ left side(s)). For better

visualization colour images are shown. Features, as previ-

ously mentioned, are extracted from depth images and point

clouds. For visualization of the nine exercises the shown

images were shot with a commercially obtainable camera

with higher resolution than the Kinect and are not part of

the dataset.

Figure 13: The 58 manually labeled landmark positions.

were removed by replacing them with the mean depth

values of adjacent valid neighbour pixels. For every

depth image, there exists a corresponding colour im-

age that has been recorded with maximum time differ-

ence of 16 milliseconds. The colour images have been

labeled manually with 58 landmark points that were

used for the training of the AAM (Figure 13) or for

the feature extraction from depth data. The transfer-

ability of landmark positions between the 2.5D image

and the colour image was further explained in sec-

tion 3.5.

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

562

4.2 Evaluation of the Discriminative

Power

The following section gives an overview of the clas-

siﬁcation results. Since we want to evaluate the ba-

sic suitability of the selected features for the task of

classifying therapeutic exercises, we extract the fea-

tures from regions obtained from manually labeled

landmarks, thus excluding other inﬂuences like devi-

ating region borders. We evaluate each feature group

individually and in combination. Training and clas-

siﬁcation is performed by applying Support Vector

Machines (SVMs) of the LIBSVM package (Chang

and Lin, 2011). We tested linear SVM and a Ra-

dial Basis Function kernel. Optimal values for the

penalty parameter C and the kernel parameter γ were

obtained by a grid search on the training set (Hsu

et al., 2009). To avoid overﬁtting to the training set,

we employed a 5-fold cross-validation during param-

eter optimization. In combination with the amount of

data (696 images, 232 feature dimensions), the lin-

ear SVM leads to the best results because it avoids

overﬁtting. The dataset was split up into training and

test set using the leave-one-out cross-validation. Ad-

ditionally, all images of the person present in the test

image are excluded from the training set. This ap-

proach is consistent with the mentioned application

scenario in which the images of the test person will

not be part of the training data. We obtained an av-

erage recognition accuracy over the nine classes of

82.4%. The use of linear discriminant analysis (LDA)

prior to the linear SVM classiﬁcation improves the re-

sults to 91.2% average recognition accuracy. LDA is

a linear transformation of the feature space that max-

imizes the between-class separability and minimizes

the within-class variablity (Webb et al., 2011). As a

result of LDA the number of feature dimensions is re-

duced from 232 to 8. Detailed results that show the

classiﬁcation accuracy for each of the nine classes are

given in Table 2.

4.3 Evaluation of Feature Extraction

from Automatically Determined

Regions

As mentioned before, in a real-world scenario regions

and landmark points for feature extraction have to

be detected automatically. Therefore, in this section

we evaluate the robustness of our features with re-

spect to varying region borders and landmark posi-

tions. Figure 14 shows the results for the three fea-

ture types for manually and automatically detected

landmarks. Automated detection was done by the

ﬁtting of AAMs. Compared to the point signatures

and line proﬁles, curvature analysis is weaker with

respect to the discrimination of the nine therapeutic

exercises. However, it achieves better results for au-

tomatically detected landmarks. The deviations of the

landmarks that were determined by AAM-ﬁtting are,

compared to the manually labeled landmarks: in x-

direction −1.88 pixels (mean value) with a standard

deviation of 4.7 and in y-direction at an average of

6.0 pixels with a standard deviation of 15.94. Consid-

ering the distances of our persons to the camera six

pixel correspond to about 0.95 centimetres. As shown

in section 3.4, the point signature needs exactly two

landmarks: the nose tip and a reference point. For

further examination of the point signatures, indepen-

dent from the AAM ﬁtting, we detect the nose tip by

curvature analysis. The reference point is determined

under the assumption that only very small in-plane ro-

tations of the face occur in our dataset. Therefore,

we estimate the reference direction by a vector par-

allel to the y-axis of the image in positive direction

(with the origin of the coordinate system in the upper

left corner of the image). Compared to the average

recognition rate that was obtain for the point signa-

tures using AAMs for landmark detection (44.5%) we

gain a signiﬁcant improvement to 72.6%. Combining

these features with the curvatures and the line pro-

ﬁles that were extracted based on the AAM an over-

all average recognition rate of 75.1% is obtained. By

only combining curvature analysis and point signa-

tures a rate of 75.6% is obtained. This shows that

the line proﬁles - in conjunction with the current au-

tomated landmark estimation method - do not con-

tribute to the classiﬁcation success. However, the re-

sults of line proﬁles using manual landmarks suggest

that further effort for more precise landmark localiza-

tions may be beneﬁcial. A certain robustness of the

line proﬁles can be assumed because even the manu-

ally labeled landmarks may be subject to deviations.

In colour images (in which the landmarks were la-

beled), especially on the chin silhouette distinctive

points are missing. Therefore, variations in position

and landmark-to-landmark distance occur on the chin

positions more likely than in the corners of the eyes

or the mouth. Figure 15 presents the comparison of

the results for the manual approach and the two auto-

mated localization methods.

5 DISCUSSION

In this paper we have discussed several aspects that

are necessary for the conception and implementation

of an automated training platform for persons with fa-

AutomatedClassificationofTherapeuticFaceExercisesusingtheKinect

563

Table 2: Confusion matrix of the classiﬁcation results (in %). Features were extracted from regions and points that have been

determined on the basis of manually labeled landmarks. The rows contain the ground truth, columns the assignments resulting

from classiﬁcation. The average recognition rate is 91.2%. LDA was applied to transform the feature space and to reduce

the feature space dimensionality. The term tongue refers to the exercise cheek boxing and cheek to cheek puffed. L and R are

abbreviations for left and right.

Pursed Taut A-Shape I-Shape Tongue L Tongue R Cheek Cheek L Cheek R

Pursed 83.75 0 1.25 0 2.5 12.5 0 0 0

Taut 2.53 81.01 0 16.46 0 0 0 0 0

A-Shape 0 0 96.43 0 0 3.57 0 0

I-Shape 0 8.33 0 91.67 0 0 0 0 0

Tongue L 0 0 0 0 100 0 0 0 0

Tongue R 4.11 0 4.11 0 0 90.41 0 0 1.37

Cheek 0 1.2 0 0 0 1.2 93.98 1.2 2.41

Cheek L 2.82 0 0 0 1.41 0 1.41 94.36 0

Cheek R 0 0 0 1.37 0 2.74 6.85 0 89.04

Table 3: Confusion matrix of the classiﬁcation results (in %). Features were extracted from regions and points that have been

determined on the basis of automatically located landmarks. The average recognition rate is 75.1%.

Pursed Taut A-Shape I-Shape Tongue L Tongue R Cheek Cheek L Cheek R

Pursed 61.25 8.75 15.00 1.25 5.00 1.25 6.25 1.25 0

Taut 1.27 70.89 2.53 21.52 1.27 0 0 0 1.27

A-Shape 5.95 2.38 82.14 7.14 1.19 0 0 1.19

I-Shape 1.39 22.22 1.39 73.61 1.39 0 0 0 0

Tongue L 8.64 2.47 1.23 1.23 81.48 4.94 0 0 0

Tongue R 1.37 5.48 4.11 5.48 0 79.45 0 0 4.11

Cheek 1.20 3.61 0 0 1.2 1.2 74.70 9.64 8.43

Cheek L 5.63 7.04 1.41 1.41 0 0 8.45 74.65 1.41

Cheek R 0 1.37 0 1.37 0 12.33 6.85 0 78.08

curvature analysis point signature line profiles

average recognition rate

manually

manually+LDA

AAM

AAM+LDA

Figure 14: The bar plot shows the average recognition rates

(in %) for each of the three feature groups. As expected

feature extraction from manually determined regions and

landmarks leads to better results than the extraction from

automatically determined areas. The local features point

signatures and line proﬁles (with LDA) lead to better re-

sults than the curvature analysis. However, they are more

prone to landmark position deviations.

cial muscle dysfuctions. We presented nine therapeu-

tic exercises, which - in cooperation with speech lan-

guage therapists - were determined as beneﬁcial for

the planned application scenario. Additionally, the

automated classiﬁcation of these exercises was eval-

uated. The presented approach employs 2.5D depth

manually AAM AAM + nose tip localization

100

average recognition rate

no LDA

LDA

Figure 15: Comparison of the average recognition rates (%)

for the nine exercises and all features. Again, rates strongly

depend on the landmark localization method. With manu-

ally labeled landmarks a rate of 91.2% is obtained. A com-

bination of the AAMs with the nose tip detection gives the

best results for the automated approaches (75.1%). In con-

trast to this, the sole use of the AAMs results in 62.9% av-

erage recognition rate.

images and 3D point clouds and is based on three dif-

ferent feature types: curvature analysis, point signa-

tures and line proﬁles. The features were evaluated

with respect to their discriminative power for exer-

cise classiﬁcation. Additionally, we examined their

robustness regarding varying locations of feature ex-

traction. This is relevant for all applications, planned

for practical use, were a manual detection of land-

marks is not feasible.

Curvature analysis, in the form we have imple-

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

564

mented it, is rather global compared to point signa-

tures and line proﬁles and showed a relatively robust

performance. However, with suitable landmark local-

izations point signatures and line proﬁles outperform

curvature analyis. We used two approaches for auto-

mated landmark detection: Active Appearance Mod-

els and nose tip estimation by curvatures. The com-

bination of both lead to the best results. Line pro-

ﬁles showed weak contribution to the classiﬁcation

process, if landmark positions are detected automat-

ically. Nevertheless, the results based on manually

deﬁned regions are promising. Besides considera-

tions of making the line proﬁles more robust, a more

sophisticated approach for automated landmark de-

tection might be the most beneﬁcial solution. Con-

strained AAMs (Cootes and Taylor, 2001) including

prior estimates of some shape point positions will

be investigated in order to improve the ﬁtting of the

AAM. Curvature analysis and a-priori knowledge re-

lated to the anatomy of the face may be valuable for

the estimation of these prior positions.

ACKNOWLEDGEMENTS

We would like to thank the m&i Fachklinik Bad

Liebenstein (in particular Prof. Dr. med. Gustav

Pfeiffer, Eva Schillikowski) and Logop

adische Praxis

Irina Stangenberger, who supported our work by giv-

ing valuable insights into rehabilitation and speech-

language therapy requirements and praxis. This work

is partially funded by the TMBWK ProExzellenz ini-

tiative, Graduate School on Image Processing and Im-

age Interpretation.

REFERENCES

Besl, P. and Jain, R. (1986). Invariant surface characteristics

for 3d object recognition in range images. Computer

Vision, Graphics, and Image Processing, 33(1):33–

80.

Chang, C.-C. and Lin, C.-J. (2011). LIBSVM:

A library for support vector machines. ACM

Transactions on Intelligent Systems and Technol-

ogy, 2:27:1–27:27. Software available at url-

http://www.csie.ntu.edu.tw/ cjlin/libsvm.

Chua, C.-S., Han, F., and Ho, Y.-K. (2000). 3d human face

recognition using point signature. In Proceedings of

the 4th Int. Automatic Face and Gesture Recognition

Conf., pages 233–238.

Chua, C. S. and Jarvis, R. (1997). Point signature: a new

representation for 3d object recognition. In Int. Jour-

nal of Computer Vision, volume 25, pages 63–85.

Colombo, A., Cusano, C., and Schettini, R. (2006). 3d face

detection using curvature analysis. Pattern Recogni-

tion, 39(3):444–455.

Cootes, T., Edwards, G., and Taylor, C. (2001). Active ap-

pearance models. IEEE Transactions on Pattern Anal-

ysis and Machine Intelligence, 23(6):681–685.

Cootes, T. and Taylor, C. (2001). Constrained active ap-

pearance models. In Proceedings of the 8th Int. Conf.

on Computer Vision, volume 1, pages 748–754.

Gebhard, A., Paulus, D., Suchy, B., and Wolf, S. (2000). A

system for diagnosis support of patients with facialis

paresis. Kl, 3/2000:40–42.

Grosse, M., Schaffer, M., Harendt, B., and Kowarschik, R.

(2011). Fast data acquisition for three-dimensional

shape measurement using ﬁxed-pattern projection and

temporal coding. Optical Engineering, 50:100503.

Haase, D. and Denzler, J. (2011). Anatomical landmark

tracking for the analysis of animal locomotion in x-

ray videos using active appearance models. In Image

Analysis, volume 6688 of Lecture Notes in Computer

Science, pages 604–615.

Hartley, R. and Zisserman, A. (2000). Multiple view geom-

etry in computer vision. Cambridge University Press.

Hsu, C., Chang, C., and Lin, C. (2009). A prac-

tical guide to support vector classiﬁcation.

TR available at http://www. csie. ntu. edu.

tw/ cjlin/papers/guide/guide. pdf.

Khoshelham, K. (2011). Accuracy analysis of kinect depth

data. In ISPRS Workshop Laser Scanning, volume 38.

Nakamura, K., Toda, N., Sakamaki, K., Kashima,

K., and Takeda, N. (2003). Biofeedback reha-

bilitation for prevention of synkinesis after facial

palsy. Otolaryngology–Head and Neck Surgery,

128(4):539–543.

Salomon, D. (2004). Data compression: the complete ref-

erence. Springer-Verlag New York Inc.

Viola, P. and Jones, M. (2004). Robust real-time face detec-

tion. Int. Journal of Computer Vision, 57(2):137–154.

Wang, J., Yin, L., Wei, X., and Sun, Y. (2006). 3d facial

expression recognition based on primitive surface fea-

ture distribution. Int. Conf. on Computer Vision and

Pattern Recognition, 2:1399–1406.

Wang, Y., Chua, C.-S., and Ho, Y.-K. (2002). Facial fea-

ture detection and face recognition from 2d and 3d

images. In Pattern Recognition Letters, volume 23,

pages 1191–1202.

Webb, A., Copsey, K., and Cawley, G. (2011). Statistical

pattern recognition. Wiley.

AutomatedClassificationofTherapeuticFaceExercisesusingtheKinect

565