
Vision-based Hand Pose Estimation
A Mixed Bottom-up and Top-down Approach
∗
Davide Periquito, Jacinto C. Nascimento, Alexandre Bernardino and Jo˜ao Sequeira
ISR - Instituto Superior T´ecnico, Universidade T´ecnica de Lisboa, Av. Rovisco Pais, Lisbon, Portugal
Keywords:
Pose Estimation, Geometric Moments, Hammoude Metric, Simulation.
Abstract:
Tracking a human hand position and orientation in image sequences is nowadays possible with local search
methods, given that a good initialization is provided and that the hand pose and appearance have small
frame-to-frame changes. However, if the target moves too quickly or disappears from the field of view, re-
initialization of the tracker is necessary. Fully automatic initialization is a very challenging problem due to
multiple factors, including the difficulty in identifying landmarks on individual fingers and reconstructing the
hand pose from their position. In this paper, we propose an appearance based approach to generate candidates
for hand postures given a single image. The method is based on matching hand silhouettes to a previously
trained database, therefore circumventing the need for explicit geometric pose reconstruction. A dense sam-
pling of the hand appearance space is obtained through a simulation environment and the corresponding sil-
houettes stored in a database. In run time, the acquired silhouettes are efficiently retrieved from the database
using a mixture of bottom-up and top-down processes. We assess the performance of our approach in a series
of simulations, evaluating the influence of the bottom-up and top-down processes in terms of estimation error
and computation time, and show promising results obtained with real sequences.
1 INTRODUCTION
Human Computer Interaction (HCI) is an active re-
search topic in computer vision community, where
the main goal is to create an easier interface by tak-
ing direct advantage of natural human skills. To man-
age this kind of interface it is necessary to achieve
precise motion measurement of various human parts
(Erol et al., 2005). In this context the hand can be
seen as an interaction device with large complexity,
over 27 Degrees of Freedom (DOF), forming a very
effective and general purpose interactive tool for HCI
(Rehg and Kanade, 1994). Hand interaction enables a
large number of advanced applications, such as sur-
gical simulations, robot interaction, virtual or aug-
mented environment interactions, among others.
To be useful in practice, HCI should embrace
a tracking algorithm capable of achieving: (i) self-
starting; (ii) accuracy for long sequences; (iii) in-
dependence regarding the activity; (iv) robustness to
drift and occlusions; (vi) computational efficiency;
and (vii) ability to operate with mobile cameras.
∗
This work was supported by the FCT projects
[PEst-OE/EEI/LA0009/2011] and VISTA [PTDC/EIAEIA/
105062/2008].
Background subtraction techniques are not recom-
mended because tracking may have to accomplished
in environments with moving background (Ramanan
et al., 2007a) (Zhiguo and Yan, 2010). The focus of
this paper is related with the automatic initialization
of the tracker in one of the most challenging problems
in HCI: human hand detection and tracking.
A number of 3D object trackers rely on Particle
Filters (PF), representing a distribution of weighted
hypotheses of object pose (Brandao et al., 2011).
However particle filters still suffer from initializa-
tion problems and recovering after occlusions. Even
small deviations from the assumed motion models can
cause tracking failure. When a particle filter starts
or is to be reinitialized, particles are often distributed
randomly in a high dimensional search space. Even
with a great number of particles, it turns out to be dif-
ficult and time consuming to initialize the tracker.
In this paper, we present a method to address this
problem by jointly using bottom-up and top-down
schemes. The algorithm initially builds a training set
with known postures. In run time the observed im-
age is matched against the trained set of hypotheses
using two matching metrics with different computa-
tional costs and precisions: first, the geometric mo-
ments (bottom-up) are able to perform a fast filtering
566
Periquito D., Nascimento J., Bernardino A. and Sequeira J..
Vision-based Hand Pose Estimation - A Mixed Bottom-up and Top-down Approach.
DOI: 10.5220/0004295805660573
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 566-573
ISBN: 978-989-8565-47-1
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

on the training set. Second, the Hammoude metric
(top-down) allows to obtain a more reliable posture
hypothesis. With this strategy, a very quick bottom-
up approach filters out most of the pose candidates
so that the more computational intensive top-down
process only has to evaluate a reduced number of hy-
potheses.
The idea of combining bottom-up and top-down
approaches has been successfully exploited in other
applications. For instance, in (Ramanan et al., 2007a),
two different methods are used to build models for
person detection. First a bottom-up approach searches
for body part candidates in the image, which are then
clustered to find and identify assemblies of parts that
might be people. Simultaneously, a top-down ap-
proach is used to find people by projecting the pre-
vious assembled parts in the image plane.
We believe that the combination of the bottom-
up and top-down processes above mentioned, is the
key for the efficiency and reliability of detection and
tracking algorithms. In one hand, the amount of im-
age information to process is huge and thus requires
top-down constraints given by models. However,
matching the models to the image must be guided by
bottom-up processes for efficiency. We evaluate our
method and study the trade-off between the bottom-
up and top-down processes in a series of simulations.
Our paper is organized as follows. Section 2 de-
scribes related work. In Section 3 we describe the
method’s architecture, which is divided in to the fol-
lowing major components: (i) the machine learn-
ing part (offline) and (ii) the matching strategy be-
tween the observed image and the generated hypothe-
ses (online). In Section 3 some experiments concern-
ing realistic scenarios is presented. Finally, Section
4 presents the conclusions of the paper and provides
directions for further research work.
2 RELATED WORK
A large number of works have been made avail-
able concerning human motion analysis, although
with different focus and classification methods. In
(Gavrila, 1999) the division is made into 2D and 3D
approaches in which the 2D approaches are further
sub-branched in methods that take advantageof an ex-
plicit use of shape models, and others that do not use
any kind of model (i. e. Image Descriptors). In recent
works (e.g. (Borenstein and Ullman, 2008), (Bran-
dao et al., 2011)), various directions in research have
emerged, such as combining top-down and bottom-up
models, PF algorithms for tracking human body parts,
and model-free approaches. Many of these newtrends
cannot be placed within the classifications mentioned
above. So, a more generic approach is proposed in
(Poppe, 2007), where the main division is made ac-
cording to model-based (or generative) and model-
free (or discriminative) approaches. The estimation
process step consists is computing the pose parame-
ters that minimizes the error between observation and
the projection of the human body model. Two classes
of estimators are possible to identify: top-down and
bottom-up (Poppe, 2007). Top-down approach con-
sists in matching a projection of the human body
model with the observed image, while in Bottom-up
approaches individual body parts are found and then
assembled into a human body image. In more recent
works (Brandao et al., 2011), (Ramanan et al., 2007b)
these two are combined for better performance
2.1 Bottom-up Estimation
Bottom-up approaches are typically used to find body
parts and then used to assemble them into a full hu-
man body; these parts are normally described as 2D
templates. The main problems associated with the
bottom-up process are normally the quantity of false
positives marked as limb-like regions in an image.
Another drawback is the need of part detectors for
most body parts since missing information is likely
to result in less accurate pose estimation.
In (Micilotta et al., 2006), the first step is to find a
person in the image, so body parts are learned by the
trackers and a possible assembly is found by applying
RANdom SAmple Consensus (RANSAC). Heuristics
are used to remove unlikely poses, and a prior pose
determines the likelihood function of the assembly.
2.2 Top-down Estimation
Top-down approaches match a projection of the hu-
man body with the image observation. In order to
achieve fast solutions, a local search is performed
in the neighbourhood of an initial pose estimation
(Gavrila, 1999). According to (Gavrila and Davis,
1996) a hierarchical classification is possible in order
to achieve better performance for initial positioning.
This way, they first build the torso and head and then
the rest of the limbs of the model.
The main constraint presented in top-down ap-
proaches is the initialization in the first frame which
leads to a manually starting requirement. Other is-
sues are the computational effort of rendering the hu-
man body model and the calculation of the distance
between the rendered model and the image observa-
tion.
Top-downapproaches also present some problems
Vision-basedHandPoseEstimation-AMixedBottom-upandTop-downApproach
567

with (self) occlusions. Therefore, the errors are prop-
agated through body parts. An inaccurate estimation
for the head part, for example, will cause big orienta-
tion errors of lower body parts. To cope with some of
these issues other techniques were used (i.e. by apply-
ing gradient descent on the cost function (Delamarre
and Faugeras, 2001)).
2.3 Combining Bottom-up and
Top-down Estimation
By combining pure top-down and bottom-up ap-
proaches, the drawbacks of both can be targeted. First
the top-down initialization can be addressed by us-
ing bottom-up methods to provide first frame infor-
mation. The computational cost to render the hu-
man body model can be drastically reduced when us-
ing bottom-up approaches to generate a small num-
ber of hypotheses, to be then tested with the top-
down models. Second, bottom-up false positives can
be removed by projecting them into the image, us-
ing top-downapproaches to reconfirm if the produced
hypothesis is correct. Top-down approaches may be
implemented in order to work as a part detector for
bottom-up estimation.
This integration is made in (Kyrki, 2005) by using
the correspondence between interest points (texture)
in the set and tracking with optical flow estimation
along contours, using the Kalman Filter (KF). In (Ra-
manan et al., 2007b) both approaches are also inte-
grated, in order to address the problem of tracking
multiple limbs of the human body. In the bottom-
up part the detection is made by a rectangular con-
tour template, which identifies possible body limb hy-
potheses, whereas the top-down approach looks for
possibilities to assemble the human body model with
the detected rectangles. The model is built taking
into consideration the constrain that limbs keep cer-
tain poses between each other.
In (Okuma et al., 2004) a mixed approach is also
applied for 2D tracking. The bottom-up layer is
achieved by implementing the Adaboost Algorithm
for object detection (in this case hockey players) and
to deal with new instances in the image. On the Top-
down method a ”mixture particle filter” (MPF) is ap-
plied in order to track multiple players. Therefore the
Adaboost is trained to detect players and combined
with the MPF to construct their distribution.
3 ALGORITHM
In this paper we combine bottom-up and top-down
processes for the detection of specific gestures and
pose estimation of a human hand. The top-down pro-
cess in encoded in templates of the hand silhouette
for a dense discretization of the pose space. Because
exhaustive template matching of all possible pose hy-
potheses is very expensive, the bottom-up process
performs a fast moment-based filtering of color blobs
in the image that are likely to contain hands on cer-
tain poses. The candidates are then ranked by quality
so that the top-down process can concentrate its re-
sources on the most promising ones. The steps of the
approach are next described in detail.
3.1 General Approach
This section describes the procedure of the proposed
framework. The creation of the top-down models
comprise a training stage with the following steps:
• Computation of the quaternions necessary to gen-
erate training hand pose hypotheses images (see
Fig. 1, most-left column). A total of 23900 im-
ages are used.
• Hand pose hypothesis are then generated in the
OpenRAVE simulator (Diankov, 2008) with an
existing humanoid 3D model. A total of 23500
images are used for training, (Fig. 1, top of the
2nd column).
• The images are segmented (i.e. the silhouettes or
contours are obtained) and corrected in perspec-
tive to simulate frontal views (Fig. 1, top of the
3rd column).
• The geometric moments of the contours are com-
puted.
• The silhouettes are stored in a database, together
with both the binary masks and the geometric mo-
ments. Also the ground truth poses (i.e quater-
nions) are stored.
The previous items are fulfilled in offline fashion.
It follows the online test step, which performs the
matching between the acquired hand silhouette (i.e
test image) and the pre-trained database of canonical
pose hypotheses described above. In run-time, each
acquired image silhouette is also pre-processed as in
the training stage (i.e. through the color segmenta-
tion process, perspective correction and binarization).
A total of 400 images are used for testing (bottom
of the Fig. 1). Then, the geometric moments of the
newly acquired mask are used to rank the training set
in descending order of match quality. We filter the
top 1000 hypotheses candidates (Fig. 1, 4th column)
that is the output of the bottom-up step of the frame-
work. It follows the top-down procedure which al-
lows a more precise match using Hammoude metric
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
568
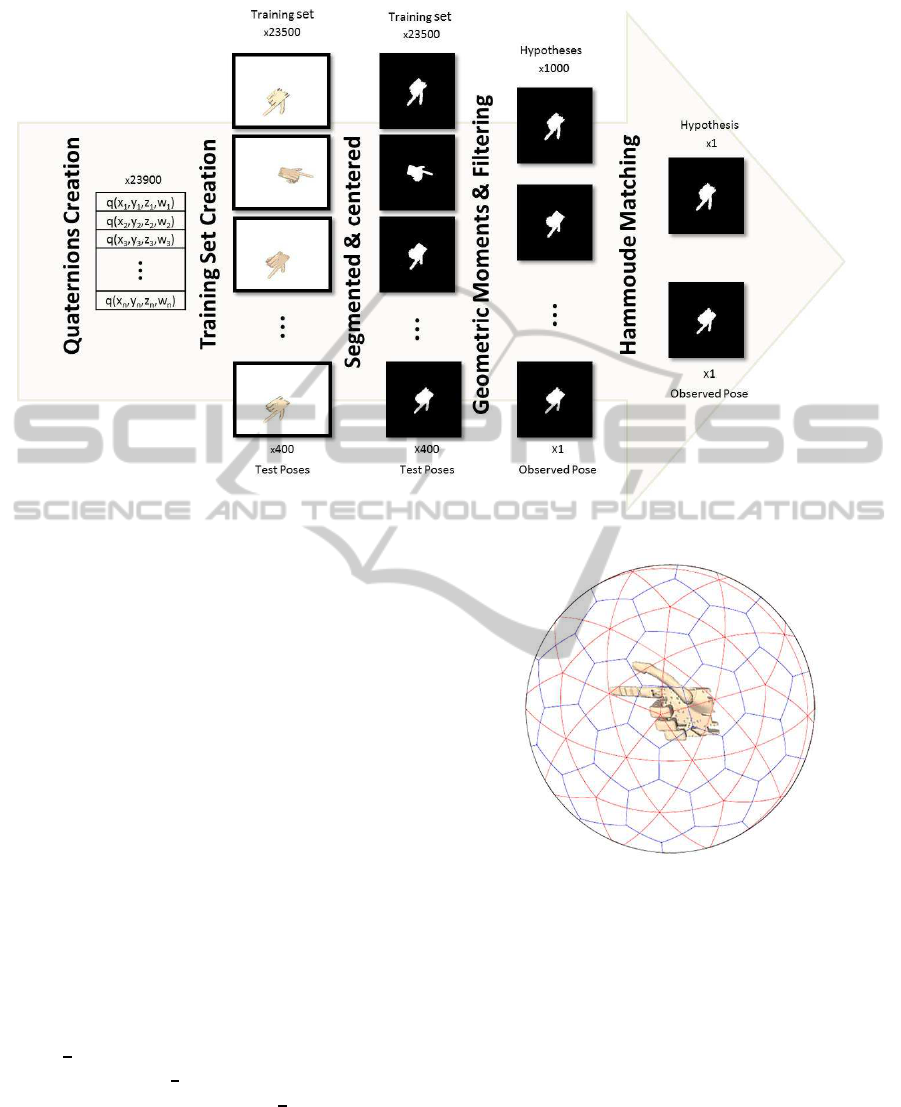
Figure 1: Algorithm architecture: an overview (see text in Section 3.1).
(Nascimento and Marques, 2008) also known as the
Jaccard distance (Hammoude, 1988). The top-down
is applied over the top ranked candidates in order to
provide for a final decision (Fig. 1, most-right col-
umn).
3.2 Training Images Generation
To generate hypotheses on OpenRAVE we place a vir-
tual camera on the simulated model looking at the 3D
hand model. By moving the camera around at a con-
stant distance to the hand we create a virtual sphere
path (see Fig. 2 for an illustration). To represent the
orientation of the camera we use a quaternion repre-
sentation. Uniform samples (see Fig. 3) on the ori-
entation sphere are generated by drawing quaternions
from a Gaussian distribution. For each sample a dif-
ference of 5
◦
(degrees) is guaranteed in the genera-
tion process. The camera rotation matrix is given by
(Shoemake, 1995):
M = 2
1
2
− y
2
− z
2
xy+ wz xz− wy
xy− wz
1
2
− x
2
− z
2
yz+ wz
xz+ wy yz− wz
1
2
− x
2
− y
2
(1)
using the restriction w
2
+x
2
+y
2
+z
2
= 1 for a quater-
nion q = [w,(x,y,z)].
Figure 2: Virtual sphere path for acquiring the training set.
The center of each hexagon corresponds to different camera
position.
3.3 Segmentation and Localization
One of the most important steps in the algorithm is
the hand segmentation. To accomplish this, we use
the HSV color space, which allows better luminosity
invariance. For the image segmentation a Histogram
Backprojection algorithm is used (Swain and Ballard,
1991), resulting in a histogram of the likelihood of
each pixel constituting the hand. Basically, this algo-
rithm assumes that a color histogram is known before
hand. The algorithm tries to localize in the image do-
main, the colors of the object being looked for. There-
fore, a salience map is created, i.e. a probability map
Vision-basedHandPoseEstimation-AMixedBottom-upandTop-downApproach
569

Figure 3: Some image samples generated with the Open-
RAVE.
for the presence of the object for each and every pixel
on the image. The histogram indicates the probability
of occurrence for the hand colors.
After the filtering process the result is a segmented
hand, though with some noise. To clean up the image
we make some image processing, by filling the holes
inside the hand and removing out border objects. Sub-
sequently we obtain a binary image with a segmented
hand. This method is identical for the training set im-
ages and for the images which we want to determine
the position – the observed (test) images.
For better matching, the hand centroid (x
0
,y
0
) is
placed in the center of the image, though for this pro-
cedure the hand has to be rotated according to the dis-
placement made before. The Homography for pro-
jecting and rotating points in an equivalent pan-tilt
camera are (Brandao et al., 2011):
x
1
=
c
t
s
p
+ c
p
x
0
− s
t
s
p
.y
0
c
t
c
p
− s
p
x
0
− s
t
c
p
y
0
(2)
y
1
=
s
t
+ c
t
y
0
c
t
c
p
− s
p
x
0
− s
t
c
p
y
0
(3)
where c
p
,s
p
,c
t
,s
t
stand for cos(p), sin(p), cos(t),
sin(t), respectively, (x
1
,y
1
) represent the pixels af-
ter the rotation, p and t are the equivalent pan-tilt
camera angles, meaning that the previous (x
0
,y
0
) are
now centered in the camera. To compute the pan and
tilt (p,t) angles the translation of the image must be
known, so:
p = arctan(x
1
) (4)
t = arctan(y
1
c
p
) (5)
ending with a segmented hand centered with the cam-
era and projected according to the movement made.
These changes of perspective introduce error in the
process though it is still acceptable.
Since we are working in a 2D image plane the Z
coordinate can be interpreted as an area normalization
factor that will be used in the matching metrics.
3.4 Pose Estimation
In order to obtain a faster algorithm, we try to com-
pute all the information needed for the estimation in
offline mode. This is accomplished by calculating the
geometric moments for the training set (bottom-up),
granting us a good filter (of the training set) in real
time application. The Hammoude metric (top-down)
will be applied next, since it provides high accuracy
but takes longer to compute.
3.4.1 Geometric Moments and their Match
To obtain fast descriptors of hand characteristics, pos-
ture and shape, we use geometric moments. These
can be made invariant to position and scale by center-
ing and normalizing by area:
u
pq
=
∑
x
∑
y
(x− x
0
)
p
(y− y
0
)
q
I(x,y)
M
1+
p+q
2
00
(6)
where u
pq
stands for the moment of order p + q, M
00
for hand area and I(x, y) for image pixel. According
to our studies, it is essential to keep the moments of
order higher than 4
th
, since the higher the order the
more discriminative characteristics we get. In con-
trast, lowerorders describe the hand position and area,
which we want to be invariant.
To get the matching distance between trained and
observed images, a Mahalanobis-likedistance is used:
d =
∑
p,q
( ˜n
pq
− n
i
pq
)
2
var(n
pq
)
(7)
˜n
pq
is the moment calculated in an observed image,
n
i
pq
the moment trained in the train set hypotheses and
var(n
pq
) is the variance of the moment in the training
set. By minimizing the function we have the most
likely hypothesis.
3.4.2 Hammoude Metric
To evaluate with higher precision the match between
the observed silhouettes and the one in the database,
we use the Hammoude metric (Nascimento and Mar-
ques, 2008; Hammoude, 1988) that is defined as fol-
lows
d
HMD
(y
1
,y
2
) =
#((R
y
1
∪ R
y
2
) \ (R
y
1
∩ R
y
2
))
#(R
y
1
∪ R
y
2
)
(8)
where R
y
1
represents the image region delimited by
the contour y
1
(similarly for R
y
2
), ♯ denotes the num-
ber of pixels within the region by the expression in
parenthesis, and \ denotes the minus operation be-
tween the sets. We then convert this value to a likeli-
hood, p(y
1
|y
2
), by:
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
570

p(y
1
|y
2
) = 1− d
HMD
(y
1
,y
2
) (9)
4 RESULTS
In this section, we experimentally validate the perfor-
mance of the top-down/bottom-up architecture for the
hand pose estimation. We first access the performance
of each component individually. Then we experimen-
tally illustrate the performance of the overall system.
4.1 Top-down vs Bottom-up
We start by illustrating the performance of the
bottom-up component. To do so, we use a previously
generated training set (23500 frames), and use a given
test hand pose image. We compute the geometric mo-
ments (see eq. (6)) for that observed image and rank
accordingly (see eq. (7)). We repeat this procedure
for all images in the test set (i.e. 400 frames). Fig. 4
shows the cumulative rank of the geometric moments
in which the bars represent the probability of hitting
the correct hypotheses (i.e. hand poses). From this
example, we see that the accuracy to first choose the
correct hypothesis is 38% (left most bar in the his-
togram). The accuracy of 90% is reached for the top
23 matched hypothesis.
To compare the obtained results with the top-down
component, we follow the same procedure (i.e. build-
ing the rank of the database for each test image).
Fig. 5 shows the achieved results for the cumulative
ranks. The performance accuracy is now 52% for the
first choice. Also, it is illustrated that a faster conver-
gence is achieved, where only 10 hypotheses suffice
for achieving 90% accuracy. This allows us to con-
clude that the top-down mechanism definitively im-
proves the quality of the detection with respect to the
bottom-up method alone.
4.2 Pose Estimation
To assess the performance of the full hand pose esti-
mation process, we first study how can we select the
proper number of candidates provided by the bottom-
up process. We have experimented numbers of candi-
dates in the set R = {1, 10, 100,1000, 10000, 23500}.
Say that, in Fig. 1 - 4th column, we vary the num-
ber of hypotheses in the range R. We then assess the
performance of the hand pose estimation by using the
top-down approach over that number of candidates.
The error metric used, is the orientation error de-
fined as
ε = 2arccos(p· q) (10)
0 10 20 30 40 50
0
0.2
0.4
0.6
0.8
1
Top Geometric Moments
% Sucess rate
Figure 4: Accumulative rank for geometric moments.
0 5 10 15 20 25 30 35 40 45 50
0
0.2
0.4
0.6
0.8
1
Top Hammoude Metric
% Success rate
Figure 5: Accumulative rank for Hammoude Metric.
where p· q stands for the inner product between two
quaternions. The error in eq. (10) is computed be-
tween the know ground truth hand pose of the test
image and the angle of maximum likelihood training
image detected by the top-down process. Finally, the
average of the orientation errors ε
AV
is taken to assess
the overall performance on the test set.
Table 1 shows the average of the orientation er-
ror ε
AV
(in degrees) and the time to compute the pose
estimation. As we can see, the time spent has a signif-
icant impact when the number of top samples grows.
For online applications this is of paramount impor-
tance, where the time should be as low as possible
2
.
Notice that, the orientation error regarding the ground
truth is remarkably under 8%, being the best value
achieved for 1000 candidate moments. However, the
error value achieved for 100 frames is quite similar,
thus being possible to use less than 1000 frames. This
allows us to conclude that the geometric moments are,
indeed, an important filtering step in order to effi-
ciently reduce the training set to just 4%. Moreover,
the integration of top-down provides higher accuracy
(as already detailed in Section 4.1) where a small ori-
entation error is obtained. Recall that, (see Section
3.2) a discretization of 5 degrees is used, meaning
that the top-down procedure exhibits remarkable ac-
2
The time results shown in Table 1 were obtained in a
non-optimized Matlab code. This could be drastically re-
duced using a C++ base programming or by optimizing the
algorithm in order to take advantage of GPU and/or by us-
ing multi-core computation.
Vision-basedHandPoseEstimation-AMixedBottom-upandTop-downApproach
571

Table 1: Mean and standard deviation (in parenthesis of the
cell) order statistics of the orientation error ε
AV
(in degrees)
and time spent ((s)-seconds, (ms)-milliseconds) for the hand
pose estimation. The experiment is repeated for the top can-
didates moments defined in the range R.
# Cand. Mom Time ε
AV
(
◦
)
1 25.2 (0) (ms) 17.8 (34.6)
10 4.21 (0.06) (s) 7.34 (15.4)
100 5.99 (0.98) (s) 5.86 (3.06)
1000 11.90 (2.74) (s) 5.77 (3.00)
10000 69.07 (5.33) (s) 5.77 (3.00)
23500 122 (8.11) (s) 6.06 (3.50)
curacy.
From Table 1 we observe that the error at the bot-
tom line grows. The reason for this is the great num-
ber of possibilities available, many ambiguous, result-
ing in very small differences for classification. This
leads to an effect similar to overfitting.
0 10 20 30 40 50
0
0.2
0.4
0.6
0.8
1
Hypotheses Candidates
% Success rate
Figure 6: Accumulative rank using top 1000 candidate hy-
potheses.
Fig. 6 shows the accumulative rank when combin-
ing the bottom-up and top-down procedures. It can be
seen that an accuracy of 90% is promptly reached us-
ing only 10 hypotheses candidates.
As a final experiment we evaluated several se-
quences in real settings. The goal is to recover the
pose of a real human hand using the model learned
with the OpenRAVE. We present the results of a se-
quence containing 50 frames. Fig. 7 shows some
snapshots of the sequence as well as the recovered
poses. We may notice some small differences be-
tween the shape of the hand (1st and 3rd rows of
the Fig.7) and the corresponding poses (2nd and 4th
rows). This happens due to the model particularities
in the generation process using the OpenRAVE (see
illustrations in Fig. 3) that is a bit different from the
human hand.
We should stress that the presence of shadows and
poor illumination in real settings can jeopardize the
silhouette recovery, leading to the incorrect hypothe-
sis given by the geometric moments and misleading
pose recovery. Although, the segmentation used in
our scenario suffices for a correct estimation, this is
Figure 7: Six snapshots of the sequence (top) poses recov-
ered by the algorithm (bottom).
an issue to take into consideration for other environ-
ments.
5 CONCLUSIONS
In this paper we proposed a 3D hand posture estima-
tion framework. The architecture combines bottom-
up and top-down approaches, providing an efficient
tool for hand orientation detection. The algorithm
presented is twofold. First, the bottom-up allows for
an efficient reduction over the training set, having a
significant impact on computationaltime. Second, the
use of the top-down process provides an improved es-
timation accuracy. Fusing these two methods we can
achieve faster performance and reliable estimation, in
both synthetic and real environments.
We conclude that this method generates a good
hypothesis estimator which is crucial for a fully au-
tomatic initialization. In future work we will focus
on the integration of this proposed methodology in a
full tracking framework (e.g. a particle filter architec-
ture) and the addition of new hand postures for more
general applications.
REFERENCES
Borenstein, E. and Ullman, S. (2008). Combined top-
down/bottom-up segmentation. IEEE transactions on
pattern analysis and machine intelligence, 30:12:4–
18.
Brandao, M., Bernardino, A., and Santos-Victor, J. (2011).
Image driven generation of pose hypotheses for 3d
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
572

model-based tracking. In 12th IAPR Conference on
Machine Vision Applications. MVA 2011.
Delamarre, Q. and Faugeras, O. (2001). 3d articulated mod-
els and multi-view tracking with physical forces.
Diankov, R. (2008). Openrave: A planning architecture for
autonomous robotics. Robotics Institute, Pittsburgh,
PA, Tech. Rep., (July).
Erol, A., Bebis, G., Nicolescu, M., Boyle, R. D., and
Twombly, X. (2005). A review on vision-based full
dof hand motion estimation. In (CVPR’05)Computer
Society Conference on Computer Vision and Pattern
Recognition.
Gavrila, D. M. (1999). The visual analysis of human move-
ment: A survey. Computer Vision and Image Under-
standing, 73:82–98.
Gavrila, D. M. and Davis, L. S. (1996). Tracking of hu-
mans in action: a 3-d model-based approach. In In
Proc. ARPA Image Understanding Workshop, pages
737–746.
Hammoude, A. (1988). Computer-assited Endocar-
dial Border Identification from a Sequence of Two-
dimensional Echocardiographic Images. PhD thesis,
University Washington.
Kyrki, V. (2005). Integration of model-based and model-
free cues for visual object tracking in 3cd. In Proc.
of the IEEE Int. Conf on Robotics and Automation
(ICRA’05), pages 1554–1560.
Micilotta, A. S., Ong, E., and Bowden, R. (2006). Real-
time upper body detection and 3d pose estimation in
monoscopic images. In In European Conference on
Computer Vision, pages 139–150.
Nascimento, J. C. and Marques, J. S. (2008). Robust shape
tracking with multiple models in ultrasound images.
IEEE Transactions on image processing, vol. 17, no.
3.
Okuma, K., Taleghani, A., Freitas, N. D., Freitas, O. D., Lit-
tle, J. J., and Lowe, D. G. (2004). A boosted particle
filter: Multitarget detection and tracking. In In ECCV,
pages 28–39.
Poppe, R. (2007). Vision-based human motion analysis: An
overview. Computer Vision and image Understanding,
108:1–17.
Ramanan, D., Forsyth, D. A., and Zisserman, A. (2007a).
Tracking people by learning their appearance. Pattern
Analysis and Machine Intelligence, IEEE Transaction
on.
Ramanan, D., Forsyth, D. A., and Zisserman, A. (2007b).
Tracking people by learning their appearance. Pattern
Analysis and Machine Intelligence, IEEE Transaction
on.
Rehg, J. M. and Kanade, T. (1994). Visual tracking of
high dof articulated structures: an application to hu-
man hand tracking. In Lecture Notes in Computer Sci-
ence, 1994, Volume 801/1994, pp. 35-46. Springer.
Shoemake, K. (1995). Animating rotation with quaternion
curves. In SIGGRAPH ’85 Proceedings of the 12th
annual conference on Computer graphics and inter-
active techniques, pages 245–254. ACM New York,
NY, USA.
Swain, M. J. and Ballard, D. H. (1991). Color indexing. Int.
Journal od Comp. Vision, 7(1):11–32.
Zhiguo, L. V. and Yan, L. I. (2010). Efficient 3d hand
posture estimation with self-occlusion from multiview
images. In 2010 Second International Conference on
Intelligent Human-Machine Systems and Cybernetics.
IEEE.
Vision-basedHandPoseEstimation-AMixedBottom-upandTop-downApproach
573
