Wavelet-based Circular Hough Transform

and Its Application in Embryo Development Analysis

Marcelo Cicconet

, Davi Geiger

and Kris Gunsalus

Center for Genomics and Systems Biology, New York University, New York, U.S.A.

Courant Institute of Mathematical Sciences, New York University, New York, U.S.A.

Keywords:

Machine Vision, Circular Hough Transform, Biological Cells.

Abstract:

Detecting object shapes from images remains a challenging problem in computer vision, especially in cases

where some a priori knowledge of the shape of the objects of interest exists (such as circle-like shapes) and/or

multiple object shapes overlap. This problem is important in the ﬁeld of biology, particularly in the area

of early-embryo development, where the dynamics is given by a set of cells (nearly-circular shapes) that

overlap and eventually divide. We propose an approach to this problem that relies mainly on a variation of

the circular Hough Transform where votes are weighted by wavelet kernels, and a ﬁne-tuning stage based

on dynamic programming. The wavelet-based circular Hough transform can be seen as a geometric-driven

pulling mechanism in a set of convolved images, thus having important connections with well-stablished

machine learning methods such as convolution networks.

1 INTRODUCTION

Information about cell division timing and cell shape

are some of the features used to analyze the early

stages of life in research and medicine. These fea-

tures are used to study the roles of different genes in

early development and to evaluate the quality of in

vitro fertilized (IVF) embryos in fertility clinics. As

data from automated time-lapse imaging of embryos

accumulates, data analysis becomes the bottleneck of

the research process Therefore, being able to count

cells and analyze their shape automatically is critical.

One may see the problem simply as that of de-

scribing shapes from a given set of points. This is

the approach of the Hough Transform (HT) (Duda

and Hart, 1972). However, the original implementa-

tion, where votes are considered pixel-wise, is very

sensitive to noise. Recent works approach the is-

sue by weighting votes with kernels (Fernandes and

Oliveira, 2008; White et al., 2010). Our method goes

in a similar direction extending it to overlapping ob-

jects and cell division. Furthermore, we propose that,

by interpreting the HT as a geometric mechanism for

pulling information from a set of convolutions, impor-

tant connections with recent developments in machine

learning algorithms can be established.

In this realm, one intuitive and recently developed

learning technique is “Deep Learning with Convolu-

tion Networks” (Hinton, 2007; LeCun et al., 2010).

Great progress was made just recently on understand-

ing this problem further with the work of Bruna and

Mallat (2012). They argue that each layer of the con-

volution network, where a convolution is applied fol-

lowed by a pooling mechanism, is equivalent to a

wavelet transform followed by the measurement of

an invariant (the magnitude of the transform). They

interpret the succession of convolution networks in

deep learning as to describe the data as a concatena-

tion of invariant descriptions of it. However, at least

one question remains: what is the “meaning” of the

last step of the convolution networks where a linear

classiﬁer is applied to the output of the last layer of

the convolution network (instead of a pooling)?

We see these issues as a source of inspiration

to propose a bottom-up model for shape detection

starting with wavelet ﬁltering, followed by a HT for

known shapes, and a dynamic programming tech-

nique to ﬁne-tune the HT results.

We apply our method to mouse-embryo cell track-

ing and division detection up to the 4-cell stage. Our

work is being used at the NYU Center for Genomics

and Systems Biology to analyze the inﬂuence of par-

ticular genes in the timing dynamics of the ﬁrst cells.

Our method performs almost twice as well as previ-

ously reported results on a similar problem (see Sub-

section 3.2).

669

Cicconet M., Geiger D. and Gunsalus K..

Wavelet-based Circular Hough Transform and Its Application in Embryo Development Analysis.

DOI: 10.5220/0004296006690674

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 669-674

ISBN: 978-989-8565-47-1

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

2 WAVELET-BASED CIRCULAR

HOUGH TRANSFORM

In the original HT, given a radius r, each edge pixel

p in the image votes for all possible centers of circles

(usually within the boundaries of the image) of radius

r passing through it.

In our implementation, given p and r, we compute

votes in a rather small “electorate”: n pixels (usually

n = 16) at equally spaced locations along the bound-

ary of the circle centered in p with radius r. The

votes of the chosen pixels are actually a weighted sum

of their neighbors’ votes, the weights being given by

a properly rotated Morlet ﬁlter, as illustrated in Fig-

ure 1.

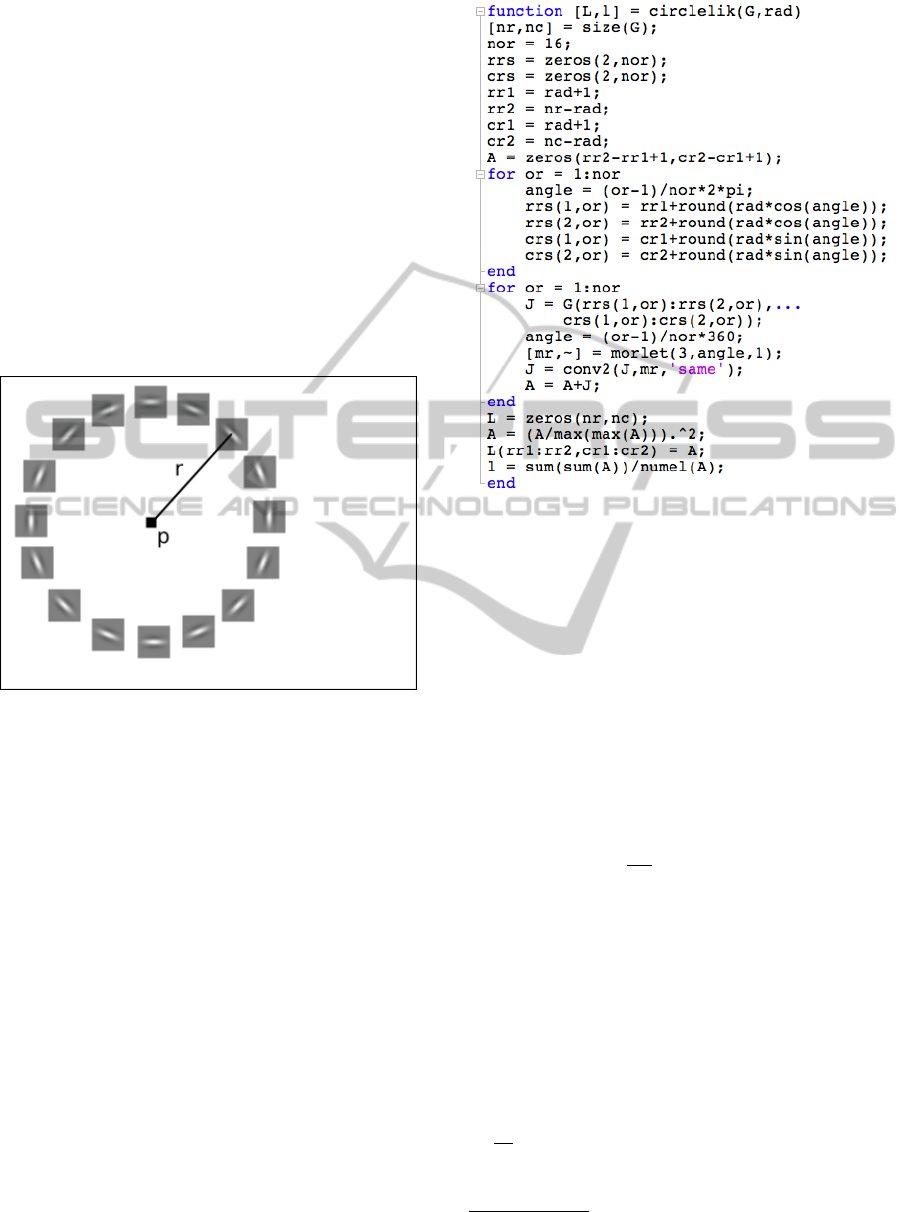
Figure 1: The likelihood that there is a circle of radius r

centered at point p depends on the votes of n (in this case

n = 16) equally spaced points along a circle of radius r cen-

tered at p. Each voting point represents its neighbors ac-

cording to a Morlet-wavelet kernel whose orientation de-

pends on its angle. The scale is chosen beforehand, based

on the size of the image.

Implementation-wise, it is better to use convolu-

tion functions and compute the votes for a particular

angle in the circle separately, adding them in the end.

If, for instance, we look for votes in 16 equally spaced

points along a circle, then 16 convolutions need to be

performed. The sub-image where each convolution

is applied depends on the angle of the point. Fig-

ure 2 shows the implementation of such convolutions

in Matlab. The function computes the accumulator

image (L), and the (inverse) likelihood (l) that an im-

age contains a circle of a particular radius.

If an image is known to have a circle of radius r,

the point where L has its maximum is the center of

that circle. The output l indicates how spread out are

the weights in L. The idea is that if there is a well-

deﬁned circle in the image, than a well-deﬁned peak

will appear in L, and the value of l will be smaller

Figure 2: Matlab implementation of the accumulator image

(L) and inverse circle likelihood (l) for the Morlet-kernel

based circular HT. G: euclidian norm of gradient of the im-

age; rad: radius; nor: number of orientations (angles) con-

sidered; morlet(): function that computes the real and

imaginary parts of a Morlet-wavelet kernel (we are using

only the real part).

than if there were no circle of that radius in the image

(see Figure 3).

Circle likelihood measures the inverse likelihood

that an image contains a circle of a particular radius.

Let A be the accumulator image obtained by the cir-

cular HT algorithm

. We deﬁne the (inverse) circle

likelihood l as

l =

∑

i=1

∑

j=1

A(i, j) ,

where m and n are the height and width of A, respec-

tively. This is of course simply the mean of the ele-

ments in A. To see why l reﬂects the inverse likeli-

hood that there is a circle of radius r in the image, let

us suppose that the accumulator A of the circular HT

was computed for radius r. We notice, ﬁrst, that A is

normalized (its maximum is 1). Now, let us sort the

elements of A according to their magnitude, obtaining

a vector that we call a, with m·n entries, ranging from

close to 0 (on the left) to 1 (on the right). The value

∑

i=1

a(i) (that is, l) is superiorly limited by 1.

If there is a circle of radius r in the image, the curve

{i,a(i)} will have a sharper peak on the far right (that

The relationship between A and L is made clear in the

algorithm shown in Figure 3.

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

670

Figure 3: We introduce a measure of the likelihood that an

image contains a circle of a particular radius. The likelihood

is based on the accumulator image of a circular HT com-

puted using Morlet-wavelet ﬁlters. The top ﬁgure shows

how the inverse of the measure varies for different radii.

The ﬁgures at the bottom show the accumulator of the HTs

for the shows radii (normalized and squared, to highlight

the peaks).

is, l will be smaller) than it would otherwise. The fact

that l is superiorly limited by 1 is important because

the size of A varies for different radii (see implemen-

tation in Figure 2).

Computing the accumulator image A can be seen

as a pulling mechanism. For each candidate to be the

center of a circle one is looking for, a number of ﬁlter

outputs are “pulled” from a bank of convolved im-

ages. The choice of convolved images and areas in

these images is stablished by the prior knowledge of

what geometrical shape one is trying to ﬁnd (in our

speciﬁc case, a circle of a particular radius).

3 APPLICATION

Morphological and kinetic features have been in-

creasingly used in in vitro fertilization clinics to im-

prove embryo quality assessment (Meseguer et al.,

2011). Those features include cleavage (division)

times, blastomere size, multi nucleation, cleavage du-

ration, lack of division in one or more cells, and cell-

boundary texture, to cite a few. Besides viability for

re-implantation, these features are also useful, in the

case of model systems like mouse-embryos, in the

study of the function of particular genes in embryonic

development.

Modern incubators are equipped with built-in

cameras designed to acquire time-lapse images of em-

bryos (at intervals of a few minutes). In general, these

videos are used by embryologists and researchers for

visual inspection, but research aiming at automati-

cally analyze them is emerging.

Two recent works (Meseguer et al., 2011; Wong

et al., 2010) focus on the correlation between re-

implantation viability and the interval between divi-

sion onsets (up to the 4- or 5-cell stage). In order to

obtain such information automatically, tracking of in-

dividual cells and detection of cell divisions are nec-

essary

In this section we show how the algorithm intro-

duced previously can be helpful in the problem of

tracking the cells and detecting cell division in the

early phases of mouse-embryo development (up to the

4-cell stage).

3.1 Cell Tracking and Division

Detection

Our method applies to a sequence of frames contain-

ing one (centralized) embryo only. The initial radius

is ﬁxed (to be 110 pixels), as the size of the ﬁrst cell

is roughly constant across embryos.

After pre-processing (adaptive histogram equal-

ization), the gradient (euclidian) norm of the image

is computed, and the result divided by its maximum,

providing an image in the range [0,1]. From this re-

sulting gradient image, a band around the initial cir-

cle is extracted. More speciﬁcally, n

equally spaced

points along the circle are sampled, and for each of

these points, n

points are sampled along the line per-

pendicular to the circle at that point, and centered at

that point. n

and n

vary according to the generation

of the cell. For the ﬁrst cell their values are n

= 160

and n

= 100. Figure 4 illustrates this process.

We then apply dynamic programming (as in

Geiger et al. (1995)) to ﬁne-tune the location of the

boundary of the cell. Figure 4 (c) shows what a solu-

tion looks like.

As the variance of the curvature of the boundary of

the cell is not high, we sample 16 “reference points”

in the resulting solution (which corresponds to the

ﬁned-tuned boundary) at equally spaced intervals, and

interpolate them using cubic splines. Examples of the

For some works that approach the problem of cell

tracking and cell-division detection in contexts other than

early embryo development, we refer the reader to Zim-

mer et al. (2002), Dzyubachyk et al. (2010), Zimmer et al.

(2002), Huh et al. (2011), and Hamahashi et al. (2007).

Wavelet-basedCircularHoughTransformandItsApplicationinEmbryoDevelopmentAnalysis

671

(a)

(b)

(c)

Figure 4: For each frame, there is an initial guess for the

circle that better approximate the boundary of each cell.

Following this circle around, a band of the original image

is taken (a) and mapped to a rectangular image. In fact,

the band of the original image is shown here just for il-

lustrative purposes. The computation of the boundary is

actually made using the band around the gradient of the

adaptive-histogram-equalized image (b). The yellow line

in (c) shows the solution by dynamic programming that ﬁts

the boundary.

Figure 5: Output of the cell-boundary ﬁtting method based

on dynamic programming.

ﬁnal result for cell boundary ﬁtting are shown in Fig-

ure 5.

The initial guess for the boundary of the cell in the

next frame is set as the circle whose center and radius

are estimated

according to the curve that best ﬁt the

boundary of the cell in the previous frame. The reason

a circle is passed to the next frame, and not the actual

boundary, is that, ﬁrst, cell boundaries are roughly cir-

cular; second, the dynamic programming step recov-

ers the minor differences in the next frame’s bound-

ary; and, third, the circle poses a global restriction for

the overall shape of the boundary, without which there

would be no safeguards for a non-plausible boundary

line (like one with self intersections). n

and n

are

computed according to the estimated radius for the

cell.

The center is the mean and the radius is the average

distance to the mean.

function rd = radiusforgeneration(g,r1)

rd = r1;

if g > 1

for i = 1:g-1

v = 4/3*pi*rdˆ3;

v = v/2;

rd = power(v/4*3/pi,1/3);

end

In the above listing, g is the generation of the cell

(1, 2, ...), and r1 is the estimated radius for a 1st gen-

eration cell. The function radiusforgeneration as-

sumes that, when a cell divides, the total volume is

kept constant

. n

is set to the integer closer to 1/4 of

the length of a circle of radius rd, and n

is set to the

integer closer to rd.

For a cell that is dividing, the current boundary

approximation should be replaced by two new bound-

aries. At this point, the accumulator image of the

wavelet-based circular HT for radius equal to the esti-

mated radius of the daughter cells is used to obtain the

ﬁrst approximation for the centers of the new cells.

Let c be the center of the cell which is dividing,

and p the farthest point in its boundary. The centers

of the new cells are estimated to be close to the line

cp (as the dividing cell is elongated in this direction).

More precisely, let d = kp −ck, and r the estimated

radius of the daughter cells. Let c

and c

be the esti-

mated centers of the daughter cells. We set

= c + (d −r)

p −c

kp −ck

, c

= c −(d −r)

p −c

kp −ck

The ﬁnal estimations for the centers of the new cells

are obtained by ﬁnding the maxima of the accumu-

lator function at the squares of edges kc

−c

√

2/2

centered at c

and c

. Figure 6 illustrates this.

We use three “experts” to decide when a cell is

dividing: pixel variances in the whole image, pixel

variances in the band around the boundary of a cell,

and the (inverse) circle likelihood (introduced in the

previous section).

Pixel variance is simply the variance of the pixel

value along a window of frames. We use a 5-frame

window in our implementation. Both the sum of the

pixel variances for the whole image and for a band

around each of the cell boundaries are observed. Fig-

ure 7 shows these two measures for some frames

around the frame where the ﬁrst cell undergoes di-

vision.

Now, if, for instance, the estimated radius for a

This hypothesis is veriﬁed to be true when the esti-

mated cell volumes are computed after tracking.

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

672

Figure 6: During division (left), the accumulator image of the circular HT with radius equal to the estimated radius of the

daughter cells is used to detect the centers of the two new cells. Regions where the new centers should be found (middle)

are estimated based on the current boundary, and the maxima of the accumulator image in these areas provide a better

approximation for the centers (right).

Figure 7: The sum of the pixel-variances in a window of 5

frames (top ﬁgure) is used (in combination with other mea-

surements) to detect a cell is dividing. The bottom ﬁgure

shows such variance computed only on a band around the

boundary of the cell. The cell divides in frame 32.

cell is r and we compute l for the circular HT cor-

responding to r in a sequence of frames, when the

cell eventually divides the value of l will increase (for

there is less evidence for a circle of radius r in the

Figure 8: The top ﬁgure shows how the inverse likelihood of

a circle of radius 113 (pixels) varies in a sequence of frames

where a cell (whose radius is approximately 113) divides.

Notice how it increases when the cell undergoes division

(frame 32). The bottom shows frames before, during, and

after cell division.

analyzed image). Figure 8 illustrates this.

Let us call v(t) and v

(t) the sum of pixel vari-

ances in the whole frame t and in the band around the

boundary of cell c in frame t, respectively. Also, let us

deﬁne l

(t) as the (inverse) likelihood curve at frame

t for a circle or radius corresponding to a cell of gen-

eration g.

The ﬁrst division is detected by looking for a

sharp increase in v(t) ·v

(t) ·l

(t). Similarly, the sec-

Wavelet-basedCircularHoughTransformandItsApplicationinEmbryoDevelopmentAnalysis

673

ond division is detected by observing a variation in

v(t) ·(v

(t) + v

(t)) ·l

(t). (At this point, c

and c

are the two current second-generation cells.) To know

which of the cells divided, v

(t) and v

(t) are com-

pared. The third division is detected by observing

v(t) ·v

(t) ·l

(t), where c

is the second-generation

cell that remained to divide.

3.2 Results

Our cell-tracking and division-detection method suc-

cessfully applies to a total of 63 embryos. Of these, 24

were used for parameter ﬁtting. That is, after the core

of the algorithm was implemented, we deployed it on

24 “training” cases, manually tuning the parameters

related with division detection in order to ﬁt the data.

After this phase, the algorithm was applied to a “test”

set comprising 150 embryos. In this set, the method

correctly performed up to the ﬁrst cell division in 91

cases (61%), up to the second cell division in 50 cases

(33%), and up to the third cell division (4-cell stage)

in 39 cases (26%).

In comparison to other works, the only method we

know of approaching a similar problem (Wong et al.,

2010) is reported to work (up to the 4-cell stage) for

14 embryos in a set of 100 (see p. 1117 of the men-

tioned reference). Apart from performance compar-

isons, we emphasize that features like the circle like-

lihood and the wavelet-based HT are more interesting

in theoretical terms, as they provide high level repre-

sentations of what happens in the (sequence of) im-

ages (as opposed to the “brute force” approach of a

particle ﬁlters tracker, for instance).

4 CONCLUSIONS

We introduced a circular HT implementation de-

signed as a pulling mechanism on a set of images con-

volved with Morlet-wavelets ﬁlters. As a byproduct

of the algorithm that computes the accumulator for

the circular HT of a particular radius, we compute the

(inverse) likelihood that an image contains a circle of

that radius.

Both the accumulator image and the circle like-

lihood are applied in a method for cell division on-

set detection and cell boundary tracking for the case

of mouse-embryos in the early stage of development

(from 1 to 4 cells). The method is in current use in a

biology lab, and outperforms previously reported re-

sults for a similar problem (see previous section).

REFERENCES

Bruna, J. and Mallat, S. (2012). Invariant scattering convo-

lution networks. CoRR, abs/1203.1513.

Duda, R. O. and Hart, P. E. (1972). Use of the hough trans-

formation to detect lines and curves in pictures. Com-

mun. ACM, 15(1):11–15.

Dzyubachyk, O., van Cappellen, W., Essers, J., Niessen, W.,

and Meijering, E. (2010). Advanced level-set-based cell

tracking in time-lapse ﬂuorescence microscopy. Medical

Imaging, IEEE Transactions on, 29(3):852 –867.

Fernandes, L. A. and Oliveira, M. M. (2008). Real-time line

detection through an improved hough transform voting

scheme. Pattern Recognition, 41(1):299 – 314.

Geiger, D., Gupta, A., Costa, L., and Vlontzos, J. (1995).

Dynamic programming for detecting, tracking, and

matching deformable contours. Pattern Analysis and

Machine Intelligence, IEEE Transactions on, 17(3):294

–302.

Hamahashi, S., Kitano, H., and Onami, S. (2007). A system

for measuring cell division patterns of early caenorhab-

ditis elegans embryos by using image processing and ob-

ject tracking. Syst. Comput. Japan, 38(11):12–24.

Hinton, G. E. (2007). Learning multiple layers of represen-

tation. Trends in Cognitive Sciences, 11:428–434.

Huh, S., Ker, D., Bise, R., Chen, M., and Kanade, T. (2011).

Automated mitosis detection of stem cell populations in

phase-contrast microscopy images. Medical Imaging,

IEEE Transactions on, 30(3):586 –596.

LeCun, Y., Kavukcuoglu, K., and Farabet, C. (2010). Con-

volutional networks and applications in vision. In ISCAS

2010), May 30 - June 2, 2010, Paris, France, pages 253–

256. IEEE.

Meseguer, M., Herrero, J., Tejera, A., Hilligsoe, K., Ram-

sing, N., and Remohi, J. (2011). The use of morphoki-

netics as a predictor of embryo implantation. Human Re-

production, 26(10):2658–71.

White, A. G., Cipriani, P. G., Kao, H.-L., Lees, B., Geiger,

D., Sontag, E., Gunsalus, K. C., and Piano, F. (2010).

Rapid and accurate developmental stage recognition of

c. elegans from high-throughput image data. In CVPR,

pages 3089–3096.

Wong, C. C., Loewke, K. E., Bossert, N. L., Behr, B., Jonge,

C. J. D., Baer, T. M., and Pera, R. A. R. (2010). Non-

invasive imaging of human embryos before embryonic

genome activation predicts development to the blastocyst

stage. Nature Biotechnology, 28:1115–21.

Zimmer, C., Labruyere, E., Meas-Yedid, V., Guillen, N.,

and Olivo-Marin, J.-C. (2002). Segmentation and track-

ing of migrating cells in videomicroscopy with paramet-

ric active contours: a tool for cell-based drug testing.

Medical Imaging, IEEE Transactions on, 21(10):1212 –

1221.

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

674