
Multi-view People Detection on Arbitrary Ground in Real-time
∗
Ákos Kiss
1,2
and Tamás Szirányi
1
1
Distributed Events Analysis Research Group, Computer and Automation Research Institute,
Hungarian Academy of Sciences, Budapest, Hungary
2
Dept. of Control Engineering and Information Technology,
Budapest University of Technology and Economics, Budapest, Hungary
Keywords:
multi-view detection, 3D position, projection, real-time processing
Abstract:
We show a method to detect accurate 3D position of people from multiple views, regardless of the geometry
of the ground. In our new method we search for intersections of 3D primitives (cones) to find positions of
feet. The cones are computed by back-projecting ellipses covering feet in input images. Instead of computing
complex intersection body, we use approximation to speed up intersection computing. We found that feet
positions are determined accurately, and the height map of the ground can be reconstructed with small error.
We compared our method to other multiview-detectors - using somewhat different test methodology -, and
achieved comparable results, with the benefit of handling arbitrary ground. We also present accurately recon-
structed height map of non-planar ground. Our algorithm is fast and most of steps are parallelizable, making
it possibly available for smart camera systems.
1 INTRODUCTION
Single camera detecting and tracking relies on some
kind of descriptors, like color, shape, and texture.
However, extraordinary and occluding objects are
hard to detect. Multiple cameras are often used to
overcome these limitations.
In these cases, consistency of object pixels among
views will signal objects in 3D space. There are many
methods for finding object pixels. Using stereo cam-
eras, the disparity map can highlight foreground, or
using wide-baseline stereo imaging, image-wise fore-
ground detection is carried out.
The resulting set of object pixels can be further
segmented, and consistency check might be reduced
to likely correspondent segments. This might be done
using color descriptors (Mittal and Davis, 2001; Mit-
tal and Davis, 2002), howevercolor calibration (Jeong
and Jaynes, 2008) is necessary due to different sensor
properties or illumination conditions.
Foreground masks can be projected to a ground
plane, and overlapping pixels mark consistent regions
(Iwase and Saito, 2004). Reliability can be improved
using multiple planes (Khan and Shah, 2009), or by
looking for certain patterns in the projection plane
∗
This work has been supported by the Hungarian Scien-
tific Research Fund grant OTKA #106374.
(Utasi and Benedek, 2011).
In many works authors assume known homogra-
phy between views and ground plane to carry out
projection. In (Havasi and Szlavik, 2011) homogra-
phy parameters are estimated from co-motion statis-
tics from multimodal input videos, eliminating the
need of human supervision.
Projection of whole foreground masks is compu-
tationally expensive, but filtering pixels can reduce
complexity. In some works, points associated with
feet are searched, reducing foreground masks from
arbitrary blobs to points and lines (Kim and Davis,
2006; Iwase and Saito, 2004).
Another gain of filtering foreground points is that
- depending on the geometry - feet are less occluded
than whole bodies, eliminating a great source of er-
rors. Reducing occlusion is especially important in
dense crowds, for example using top-view cameras
(Eshel and Moses, 2010).
2 OVERVIEW
Our goal was to design an algorithm for detect-
ing people in a multiview environment with possibly
many views where the geometry of the ground is ar-
bitrary, which problem is not addressed in the field.
675
Kiss Á. and Szirányi T..
Multi-view People Detection on Arbitrary Ground in Real-time.
DOI: 10.5220/0004296506750680
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 675-680
ISBN: 978-989-8565-47-1
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

(a) (b) (c)
Figure 2: Steps of extracting ellipses covering feet: (a) foreground detection, (b) finding candidate pixel set, (c) forming
ellipses covering these pixel sets (ellipses are visualized with lozenges).
Figure 1: Shadows may corrupt foreground detection even
in carefully chosen color space.
Moreover we aimed at reaching real-time running to
make it available for surveillance systems.
Foreground pixels of a view correspond to lines in
3D scene space, and lines intersect in scene space at
points inside the object. However, computing inter-
sections would be slow due to large number of line
pairs.
1. Number of line pairs can be decreased by filter-
ing foreground mask. We selected candidate pix-
els for feet, drastically reducing number of fore-
ground pixels.
2. We clustered candidate pixels so that clusters
cover feet. These clusters are modeled with el-
lipses, which can be back-projected to cones in
scene space. Finding intersecting cones replaces
pairwise matching of lines in cluster-pairs.
Our approach has several advantages in means of
both precision and speed:
• for determining cone parameters, undistortion
may be carried out with few computations lead-
ing to accurate parameters,
• unlike pixels, number of clusters is proportionalto
number of objects regardless of image resolution,
• ground doesn’t have to be flat (unlike using ho-
mographies in (Utasi and Benedek, 2011; Khan
and Shah, 2009; Khan and Shah, 2006; Iwase and
Saito, 2004; Berclaz et al., 2006)),
• no presumption on height range is required -
which is mandatory in (Utasi and Benedek, 2011;
Khan and Shah, 2009; Khan and Shah, 2006)
On the downside:
• our algorithm may fail on incorrect foreground
mask, when extracted ellipses won’t cover feet
precisely - as shown in Section 3.2.
• precise calibration is required for reliable estima-
tion of cone parameters (both intrinsic and extrin-
sic parameters of the camera).
We show applied preprocessing steps to form el-
lipses from foreground mask in section 3. Section 4
introduces steps of forming cones in scene space and
matching these cones. Section 5 describes feet detec-
tion from cone matches as well as details of height
map reconstruction. We show results and comparison
to state of the art methods in Section 6 and conclude
our work in Section 7.
3 PREPROCESSING
We used a modified version of the foreground detector
described in (Benedek and Szirányi, 2008) by adding
white balance compensation to the model. This re-
duced artifacts due to self-adjustment of camera.
We filtered out small areas (less than 7px in our
experiments) from the foreground mask to suppress
noise - different threshold might be best for different
videos.
We tried several color spaces, eliminating shad-
ows and reflections on the ground was most reliable
in XYZ color space. We used this in our experiments,
however, in certain situations foreground mask was
still corrupt, Fig 1 shows an example.
3.1 Filtering Feet from Foreground
Mask
Assuming camera is in upright position, pixels of feet
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
676

Figure 3: Candidate pixels can appear on arms or on fore-
ground artifacts, and also cones corresponding to different
feet can intersect.
are bottom pixels of vertical lines in the foreground
mask. We call these candidate pixels. A sample of
extracted candidate pixels can be seen in Fig 2(b).
Candidate pixels are usually not adjacent, because
of noise and steep edges. None of these depend on
image resolution, distance threshold is chosen accord-
ing to image quality. In our case, we connected pixels
closer than 3px to form clusters.
This makes our algorithm robust to image resolu-
tion, as increasing resolution results in more candi-
date pixels, but the same number of clusters. Reduc-
ing the number of 3D primitives, drastically speeds up
pairwise matching.
3.2 Forming Ellipses
We model every cluster - pixel set - with an ellipse
according to moments of the pixel coordinates. For
an ellipse with major and minor radii a and b parallel
to axes, we know:
R
x
2
dA =
a
3
bπ
4
(1)
R
y
2
dA =
ab
3
π
4
(2)
R
xydA = 0 (3)
Rotating with α we get:
x
′
y
′
=
c −s
s c
x
y
(4)
tg2α =
2
R
x
′
y
′
dA
R
y
′2
dA −
R
x
′2
dA
(5)
a
2
= 4
R
x
′2
dA +
R
y
′2
dA +
R
x
′
y
′
dA
sc
R
1dA
(6)
b =
R
1dA
aπ
(7)
Where s = sinα, c = cosα. We rejected too small
and upright ellipses, these don’t correspond to feet.
Sample results can be seen in Fig. 2(c).
4 FINDING INTERSECTIONS
We back-projected ellipses in images to cones in
scene space. Cones corresponding to a foot will inter-
sect close to the location of foot. However, candidate
pixels can also appear on arms or on foreground arti-
facts, and accidental intersections lead to false posi-
tives. Fig 3 shows such examples.
4.1 Forming Cones
We chose to describe a cone with a vertexC and three
orthogonal vectors u, v and w, where w is the unit
length direction vector of axis and u, v are direction
vectors of major and minor axes. Bevel angles are de-
termined by the length of u, v vectors. Cone consists
of points p where
(p−C)u
2
+
(p−C)v
2
≤
(p−C)w
2
,
(p−C)w ≥ 0
(8)
For a calibrated camera, we know 3D position of
points of image plane as well as the optical center O.
Thus computing w is straightforward. u
i
, v
i
point to-
wards extremal points of ellipse in image plane, vec-
tor products ensure orthogonality of u, v, w vectors.
Finally, u and v are scaled according to major and mi-
nor bevel angles so that (8) stands.
v = αu
i
× w (9)
u = βw× v (10)
4.2 Cone Matching
Intersection of cones is a complex body, but we found
it is not necessary to know it exactly, just to measure
the degree of intersecting. Thus we simplified match-
ing in two ways:
(1) Feet are small in images, so bevel angles of cones
will be small. Consequently, cones can be approxi-
mated with elliptical cylinders near intersection:
(p−C)u
′
2
+
(p−C)v
′
2
< 1 (11)
u
′
= u|
−−−−→
CP
close
|, v
′
= v|
−−−−→
CP
close
|
(12)
Where
−−−−→
CP
close
is the distance of vertex closest to
other cone’s axis (see Fig. 4).
(2) Exact intersection of elliptic cylinders is still com-
plex, therefore we tried to find an optimal point p in
space, for which distance from cylinder axes is mini-
mal - considering different major and minor radii.
Distance from axis - left side of (11) - is a linear
function of p, enabling us to write a linear equation
Multi-viewPeopleDetectiononArbitraryGroundinReal-time
677

u
v
w
a
1
a
2
d(a
1
, a
2
)
C
P
close
Figure 4: Elliptical cylinder for cone matching.
system expressing p
is on both axes (index refers to
cylinders):
(p− C
1
)u
′
1
2
+
(p−C
1
)v
′
1
2
= 0,
(p− C
2
)u
′
2
2
+
(p−C
2
)v
′
2
2
= 0
(13)
Equivalent to
u
′T
1
v
′T
1
u
′T
2
v
′T
2
p =
u
′
1
C
1
v
′
1
C
1
u
′
2
C
2
v
′
2
C
2
Ap = b
(14)
Of course, axes will practically never intersect,
only approximate solution is possible. Solving sub-
ject to least square error is straightforward, as it min-
imizes sum of square distance from axes considering
major and minor radii, and can be computed fast - we
used pseudo inverse.
If p is outside any cylinder, we conclude cones are
not intersecting, otherwise, they intersect and p is the
position of the intersection - which we call match. We
used error as the measure of degree of intersecting.
5 DETECTING FEET
A single object may result in multiple matches, close
to each other. To avoid multiple detections, we
merged close matches. We put merged set in the bari-
center of matches, and we assigned a weight in a way,
that the possibility of detection highly increases with
the number of matches.
Matches - single or merged - with weights above a
given threshold will form a detection. This threshold
balances the tradeoff between precision and recall.
5.1 Reconstructing Height Map
We found that in a dense crowd many false detections
appear due to corrupt foreground mask or acciden-
tal intersections (as in Fig 3). However the height of
these detections is quite random.
Consequently these false positives appear as a
noise, that can be suppressed using statistical filtering
on a long video. Regions in space with many accumu-
lated detections will determine ground, we call these
height points. Height map consists of these height
points.
The phrase height map is somewhat misleading,
because at surface borders, it is possible to have mul-
tiple height points above each other, however in our
tests this never occurred.
A sample height map of our non planar test case
is shown in Fig 5. There are certain areas where few
detections took place, this led to incomplete height
map.
Figure 5: Generated height points for our test case.
False positives tend to occur far from the ground,
ignoring detections far from height map drastically
improves performance.
6 EXPERIMENTS
Test sequences commonly used for multiview detec-
tion contain planar ground. Therefore we made test
videos of a non planar ground to demonstrate capabil-
ities of our method. We used four different consumer
digital cameras with video capture function, and syn-
chronized videos using a bouncing ball. We found
that our algorithm performed well despite the differ-
ent camera parameters, distortion and image quality.
We tested our algorithm on EPFL terrace (EPFL,
2011) (sample results can be seen in Fig 6), and
SZTAKI (our own) sequences.
Detecting feet has advantages: (1) feet are al-
ways near ground, this enables us to compute and use
height map, (2) in certain camera setups, feet are less
likely to be occluded compared to whole bodies.
On the downside, accurate synchronization is
mandatory, because slight time skew leads to errors
comparable to the foot itself, preventing detection.
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
678
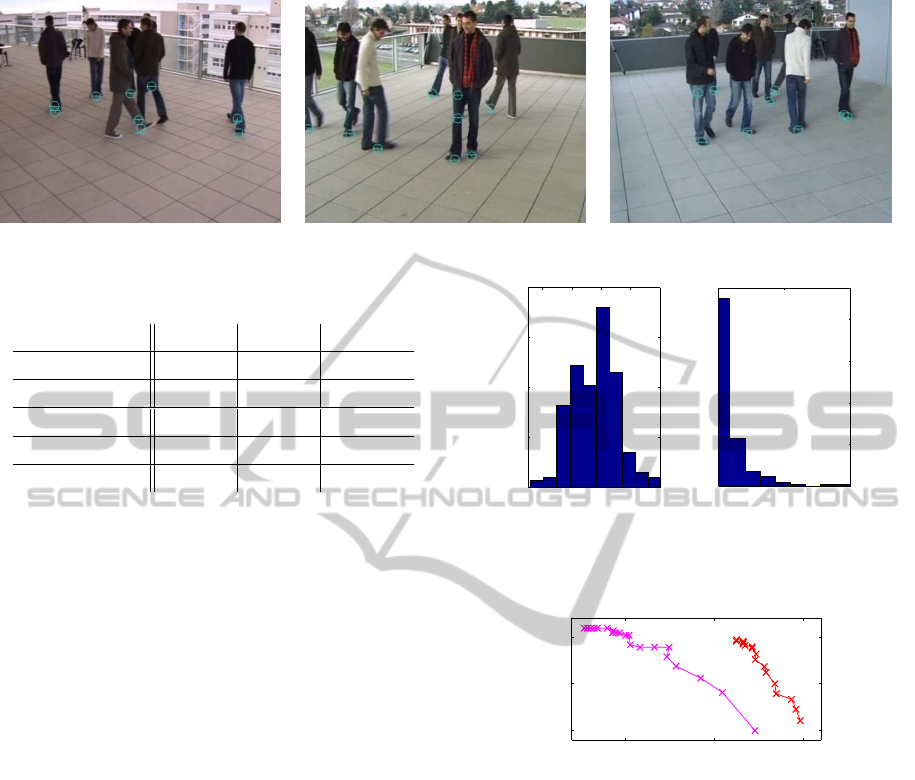
Figure 6: Corresponding frames from different cameras with the detected feet marked.
Table 1: Statistical information on surfaces found in scene.
surface floor box table top
height
0cm 50cm 73cm
µ 0.6cm 49.7cm 73.9cm
σ 1.7cm 0.6cm 1.2cm
nr. of points 131 6 23
maximal error 10.7cm 1.4cm 3.2cm
6.1 Height Map Reconstruction
We found height map could be reconstructed pre-
cisely for both sequences. Height points from EPFL
dataset fit well to a plane (σ = 1.5cm), height his-
togram is shown in Fig 7(a).
For our sequence, all three surfaces were found
with high accuracy, measurements are summarized in
Table 1. Few outliers lead to great maximal error in
floor (see Fig 7(b)).
6.2 Detecting People
We tested our method using manually created ground
truth information of feet positions. For a person, one
or two legs can be specified, because sometimes only
one foot is visible from more views.
Evaluation was carried out by matching detections
to feet inside a region of interest (ROI). ROI is de-
fined by a rectangle on floor so that every part is vis-
ible from at least three views (EPFL dataset provides
ROI, for SZTAKI set we manually determined it).
Detection was accepted if it was not further than
25cm from a foot position - approximately the length
of a foot. Unaccepted detections appear as false posi-
tives. As we detect persons, false negatives are people
with none of their feet detected.
Detection threshold balances number of false pos-
itives/negatives. Therefore we measured precision-
recall values in function of this threshold, Fig. 8
shows resulting ROC curves. Our experiments
−20 0 20 40 60
0
20
40
60
80
height (mm)
(a)
0 50 100
0
20
40
60
80
height (mm)
(b)
Figure 7: Histogram of height of floor for (a) EPFL and (b)
SZTAKI datasets.
0.85 0.9 0.95
0.85
0.9
0.95
Precision
Recall
Figure 8: ROC curve measured in function of detection
threshold on terrace (red), and our test videos (magenta).
showed reflective surfaces were liable for worse re-
sults for our dataset.
With this evaluation method, our results became
comparable to other multiview detection methods
- where people are detected instead of feet. We
found our results are comparable to SOA methods
POM(Fleuret et al., 2008) and 3DMPP(Utasi and
Benedek, 2011) (evaluated in (Utasi and Benedek,
2011) on EPFL and PETS datasets), in case of pla-
nar ground. Table 2 shows results.
6.3 Running Time
Table 3 shows average running times of steps of our
algorithm (at video resolution of 360× 288 for EPFL
and 320 × 240 for SZTAKI sequences). As we can
see, real-time operation is possible even for single
Multi-viewPeopleDetectiononArbitraryGroundinReal-time
679

Table 2: Comparison to SOA methods.
method POM
a
3DMPP
a
Our method
b
Precision 87.20 97.5 91.28
Recall 95.56 95.5 95.01
a
evaluated on EPFL and PETS sequences (Utasi and
Benedek, 2011), 395 frames with 1554 objects
b
evaluated on EPFL sequence, 179 frames with 661
objects
Table 3: Average processing time of steps (4 views, single
threaded implementation, 2.4GHz Core 2 Quad CPU).
EPFL SZTAKI
foreground detection 51.2ms 32.5ms
forming cones 3.43ms 4.87ms
matching/detection 907us 618us
threaded implementation.
However, foreground detection and forming cones
can be done independently for views, on multicore
platforms or even on smart cameras. Matching and
detection requires all cone information, but is ex-
tremely fast, real-time processing would still be pos-
sible with more views.
Many methods, including POM and 3DMPP,
project parts or whole foreground masks to planes,
which is computationally expensive, and distributing
computation is not possible due to data dependencies.
7 CONCLUSIONS
We proposed a multiview-detection algorithm that re-
tracts 3D position of people using multiple calibrated
and synchronized views. In our case, unlike other al-
gorithms, non-planar ground can be present. This is
done by modeling possible positions of feet with 3D
primitives, cones in scene space and searching for in-
tersections of these cones.
For good precision, height map of ground should
be known. Our method can compute height map on
the fly, reaching high precision after a startup time.
After height map detection we measured preci-
sion and recall values comparable to SOA methods
on commonly used data set. Our algorithm worked
well also on our test videos we made to demonstrate
capabilities of handling non-planar ground.
In the future we plan to examine tracking people
by their leaning leg positions(Havasi et al., 2007).
REFERENCES
Benedek, C. and Szirányi, T. (2008). Bayesian foreground
and shadow detection in uncertain frame rate surveil-
lance videos. IEEE Image Processing, 17(4):608–621.
Berclaz, J., Fleuret, F., and Fua, P. (2006). Robust people
tracking with global trajectory optimization. In IEEE
CVPR, pages 744–750.
EPFL (2011). Multi-camera pedestrian videos.
http://cvlab.epfl.ch/data/pom/.
Eshel, R. and Moses, Y. (2010). Tracking in a dense
crowd using multiple cameras. International Journal
of Computer Vision, 88:129–143.
Fleuret, F., Berclaz, J., Lengagne, R., and Fua, P. (2008).
Multicamera people tracking with a probabilistic oc-
cupancy map. IEEE Trans. Pattern Anal. Mach. In-
tell., 30(2):267–282.
Havasi, L. and Szlavik, Z. (2011). A method for object lo-
calization in a multiview multimodal camera system.
In CVPRW, pages 96–103.
Havasi, L., Szlávik, Z., and Szirányi, T. (2007). Detec-
tion of gait characteristics for scene registration in
video surveillance system. IEEE Image Processing,
16(2):503–510.
Iwase, S. and Saito, H. (2004). Parallel tracking of all soccer
players by integrating detected positions in multiple
view images. In IEEE ICPR, pages 751–754.
Jeong, K. and Jaynes, C. (2008). Object matching in disjoint
cameras using a color transfer approach. Machine Vi-
sion and Applications, 19:443–455.
Khan, S. and Shah, M. (2006). A multiview approach to
tracking people in crowded scenes using a planar ho-
mography constraint. In ECCV 2006, Lecture Notes
in Computer Science, pages 133–146.
Khan, S. and Shah, M. (2009). Tracking multiple occluding
people by localizing on multiple scene planes. PAMI,
31(3):505 –519.
Kim, K. and Davis, L. S. (2006). Multi-camera tracking
and segmentation of occluded people on ground plane
using search-guided particle filtering. In ECCV, pages
98–109.
Mittal, A. and Davis, L. (2001). Unified multi-camera de-
tection and tracking using region-matching. In IEEE
Multi-Object Tracking, pages 3 –10.
Mittal, A. and Davis, L. (2002). M2tracker: A multi-view
approach to segmenting and tracking people in a clut-
tered scene using region-based stereo. In ECCV 2002,
pages 18–33.
Utasi, Á. and Benedek, C. (2011). A 3-D marked point pro-
cess model for multi-view people detection. In IEEE
CVPR, pages 3385–3392.
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
680
