Statistical Inverse Lighting

Eduardo Fern

andez

and Gonzalo Besuievsky

Centro de C

alculo, Universidad de la Rep

ublica, Montevideo, Uruguay

Geometry and Graphics Group, Universitat de Girona, Girona, Spain

Keywords:

Inverse Lighting, Radiosity.

Abstract:

Inverse lighting techniques allows to obtain the unknown light sources parameters, such as light position or

ﬂux emission, from desired lighting intentions. In this paper we present a new inverse lighting technique that

uses the statistical mean and variance of the illuminated scene to obtain optimal solutions for a given lighting

intention. This technique allows to explore a huge number of full radiosity solutions in a short time, reducing

in this way drastically the optimization time required.

1 INTRODUCTION

Lighting intentions (LI) are the goals that designers

would like to achieve in the illumination design pro-

cess. Given an interior space to illuminate, this pro-

cess achieves several steps that goes from the use of

the space to the speciﬁc light accentuation to be ob-

tained (Russell, 2008). Once the LIs are speciﬁed the

designer provides the set of parameters that must ful-

ﬁll the intentions. Then, the light positions, shape and

power of the emitters, must be selected.

The management of all lighting parameters is a

huge combinatorial problem. Usually, to ﬁnd a so-

lution, the problem is treated as an inverse method.

That is, a method where the illumination aspects are

unknown and must be determined. The whole process

involves two main computational tasks: the global il-

lumination simulation and the search of an optimal

solution. The ﬁrst one is crucial to obtain accurate

lighting information. For the second one, an opti-

mization process is used to fulﬁll the requirements.

Most of the previous work on inverse lighting for

global illumination problems provides good numer-

ical methods, omitting timing considerations, which

can be a problem for interactive design.

In this paper we present a new inverse lighting

method, that focus on the use of statistical LI and

that greatly improves timing of previous work. Our

main contribution is to introduce a new technique

that relates LIs to the lighting mean and variance of

the scene. Our method exploits coherence of inte-

rior spaces to build a compact radiosity representa-

tion that is efﬁciently used to quickly explore many

lighting solutions. We present previous work is in

Section 2 and the background for lighting represen-

tation we used in Section 3. Our statistical approach

is introduced in Section 4 and test results are shown

in Section 5. Finally, conclusions and future work are

summarized in Section 6.

2 PREVIOUS WORK

One of the ﬁrst attempts to infer emitter positions

and shapes given lighting intentions, is presented in

(Schoeneman et al., 1993) through the intuitive prin-

ciple of ”Painting with light”, but where the interac-

tivity is achieved only for direct illumination. In our

work we are focusing on indirect illumination.

In the context of radiosity, several works driven by

different motivations and assumptions were proposed.

A survey on all these methods can be found in (Patow

and Pueyo, 2003). In (Contensin, 2002), an Inverse

Radiosity method based on a pseudo-inverse of the

radiosity matrix is formulated. Kawai et al. (Kawai

et al., 1993) perform the optimization over the intensi-

ties and directions of a set of lights, as well as surface

reﬂectivity, in order to best convey the subjective im-

pression of certain scene qualities expressed by users.

In (Castro et al., 2012), an heuristic search algorithm

combined with linear programming is used to opti-

mize light positioning with an energy-saving goal.

In all inverse lighting methods the coherence is

used to improve the global illumination computation.

In (Castro et al., 2012), a re-using random walk paths

technique is employed. They store an irradiance ma-

185

Fernández E. and Besuievsky G..

Statistical Inverse Lighting.

DOI: 10.5220/0004297501850190

In Proceedings of the International Conference on Computer Graphics Theory and Applications and International Conference on Information

Visualization Theory and Applications (GRAPP-2013), pages 185-190

ISBN: 978-989-8565-46-4

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

trix that allows computing, for each patch of the scene

the power contribution of ﬁxed light points. We based

our work on the low-rank radiosity method (LRR)

(Fern

andez, 2009), that allows to obtain a full radios-

ity solution in real time with changing lighting param-

eters and small computer storage.

Our work deals also with optimization problems.

These problems consists of ﬁnding the best solution

from all of the feasible solutions, which are deﬁned

through a set of constraints. For illumination pur-

poses, each constraint is related to a lighting intention

for all or part of the scene. To ﬁnd an optimal solu-

tion, heuristic approach are used, which avoid visit-

ing the whole search space. There are a large number

of heuristic search algorithms in the literature, which

can potentially be used to solve lighting problems

(hill climbing, beam search and simulated annealing)

(Russell and Norvig, 2003). In (Castro et al., 2012)

a wide range of these algorithms are explored. In

(Cassol et al., 2011) and (Schneider et al., 2009), the

scenes are simpliﬁed to rectangular spaces, and the

inverse problem is solved through a generalized ex-

tremal optimization approach. In (Fern

andez and Be-

suievsky, 2012), the Variable Neighborhood Search

(VNS) method (Hansen and Mladenovic, 2001) was

used. We also used VNS for the present work.

3 COMPACT LIGHTING

REPRESENTATION

Lighting intentions (LI) are deﬁned as goals that de-

signers must provide to achieve the desired illumina-

tion. Designers can set many LI. Examples of LIs

are: ”Guarantee a minimum of irradiance in a panel

in order to be seen correctly” or ”Distribute the light

homogeneously over all surfaces” (Figure 1).

In the discrete radiosity problem, the radiosity of

the scene is computed by solving the linear system

shown in Eq. 1 (Cohen et al., 1993).

(I − RF)L

= E (1)

where I is the identity matrix with dimension n×n (n

is the number of patches), R is a diagonal matrix that

stores the reﬂectivity of the patches, F is the form fac-

tors matrix, L

is a vector with the radiosity values,

and E is the emission vector. The designer goal is to

ﬁnd E (to conﬁgure the position and radiosity values

of the light sources), so that L

meets all LI.

Usually the F matrix is not computed, due to

memory constraints. The n×n matrix M of Eq. 2 also

has high order of complexity, so is rarely computed.

= ME (2)

Figure 1: A top-view scene with a lighting intention conﬁg-

uration example (top) and a possible solution for position-

ing four light sources (bottom).

In this paper we use information from the M ma-

trix to deﬁne LIs, for this purpose, so we use the

low-rank radiosity (LRR) methodology (Fern

andez,

2009). In LRR the matrix F is aproximated by the

product of two matrices (UV

), with dimension n×k

(nk). The O(nk) memory needed, allows storing U

and V

in the main memory. This work also exposes

an approximation of the M matrix (see Eq. 3) intro-

ducing Y, which is also a n×k matrix.

= ME ∼



I − YV



E (3)

where Y = −RU



I − V



−1

4 STATISTICAL BASED LI

In statistics (Canavos, 1984), the mean (µ) and the

standard deviation (σ) are used to describe properties

about sets of numerical data. µ describes the central

tendency of the data and σ measures their dispersion.

In this paper is used µ and σ to describe LIs. We show

that µ(L

(s)) and σ(L

(s)) could be obtained without

the previous calculation of L

(p) for patches p be-

longing to the scene s. Here we explain the calcula-

tion process of µ and σ, and how can be used in LI.

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

186

4.1 Mean (µ) of L

(s)

Radiosity is deﬁned as light ﬂux per unit of surface,

so it is the mean (weighted by the area of the patches)

of the ﬂux density on all patches (Eq. 4).

µ(L

(s,E)) =

∑

p∈s

(i,i)L

(p,E) =

M)E = V

(s) · E (4)

In Eq. 4, W

is a diagonal matrix with weights

(i,i) = A(i,i)/

∑

A( j, j)). V

(s)

is a n×1 vector.

In the calculation of the radiosity on a static

scene the vector V

(s) does not varies. In summary,

µ(L

(s)) can be computed with complexity O(n), us-

ing a single dot product.

4.2 Standard Deviation (σ) of L

(s)

The standard deviation (σ) is a scale parameter which

determines the dispersion of a data set. Any radios-

ity vector can be interpreted as a list of sample data

of a “random variable L

” which varies on a surface.

Figure 2 shows an E-shaped scene with ﬁve different

conﬁgurations of lights. Each L

has its own σ(L

)

value, which measures the dispersion of the radiosity

values along each scene. The more homogeneously

illuminated the scene, the lower σ(L

) associated, be-

cause of the small dispersion of the L

lighting values.

(a) σ = 0.43 (b) σ = 1.03 (c) σ = 1.52

(d) σ = 2.1 (e) σ = 3.51

Figure 2: Different radiosity distributions in the ”E” scene

(n=24736), and their σ values. Red patches are the emitters.

To speed up the calculation of σ(L

), we consider

as a linear combination of random variables: the

vector L

can be deﬁned as a linear combination of

the M columns (Eq. 5):

= ME =

∑

M(:,i)E(i) (5)

where M(:,i) is the sample data of an i

random vari-

able. Also is important the relation between the vari-

ance and the covariances, as expressed in Eq. 6.

var(

∑

) =

∑

i j

cov(L

, (6)

In Eq. 6, L

and L

are random variables, a

and a

are

constants, and cov is the covariance between L

and

. Then, Eqs. 5 and 6 can be combined as:

var(L

) = var(

∑

M(:,i)E(i)) =

∑

i j

cov(M(:,i),M(:, j))E(i)E( j) = E

cov(M)E (7)

In equation Eq. 7, cov(M) is a n×n covariance ma-

trix, where each element cov(M)(i, j) is the covari-

ance associated with the i

and j

variables of M

(with sample data M(:,i) and M(:, j)).

4.3 Low-rank Covariance Matrix

In Eq. 7, cov(M) concentrates all geometric infor-

mation, so, when the geometry is static it can be cal-

culated in a precomputation stage. But an impor-

tant drawback of this equation is the O(n

) memory

needed to store cov(M). Fortunately, because of the

lighting coherence in the scenes, the correlation be-

tween lighting data of close patches is high, so the

cov(M) is a numerically low-rank matrix. Figure 3

shows the covariance matrix and its singular value de-

composition (SVD) of a Cornell box. It can be appre-

ciated that cov(M) has many pairs of similar rows.

The plot of the SVD values (Figure 3 (b)) conﬁrms

that it is composed with redundant information.

To build a smaller covariance matrix, we replace

the matrix M in Eq. 7 by its low-rank variant YV

(Eq. 3) producing a k×k covariance matrix (Eq. 8).

var(L

) ∼ var(YV

E) =

var(

∑

Y(:,i)(V

) = (V

cov(Y)(V

E) (8)

In this equation (V

E) is k×1 and (V

is the i

el-

ement. Also, each column Y(:,i) contains the sample

values of a random variable. Finally, cov(Y) is the

k×k covariance matrix associated to those variables.

A brute force calculation of var(L

) using Eq. 8

consumes O(nk) operations. This result is higher than

the complexity obtained for µ calculation. As stated

in (Fern

andez et al., 2012), for any scene with coarse

and ﬁne-grained meshes, it is possible to built a sparse

StatisticalInverseLighting

187

(a) cov(M(s,:)) (white ≡ 0 value).

(b) Singular values of cov(M(s,:)).

Figure 3: Covariance matrix and its SVD decomposition for

a Cornell box with 3584 patches.

matrix V such that the complexity of V

E product

could be reduced to O(n). So, through a careful use of

Eq. 8, the complexity of the variance can be reduced

to O(n + e

) where e is the number of emitter patches

in the coarse-grained mesh.

4.4 Chebyshev’s based Constraints

A designer may want to optimize the lighting scene

using certain LI, wishing to minimize the consump-

tion of artiﬁcial light, but also bounding the light lev-

els or the contrast. All these LI can be transformed

into optimization goals and constraints, using µ and

σ parameters. For instance, to control a given con-

straint to be fulﬁlled (L

min

≤L

(p)∀p ∈ s), we have to

calculate all the L

(p) values, which has complexity

O(nk). A O(n) option consists in ﬁnding µ(L

(s))

and σ(L

(s)) to bound the probability of any p to ful-

ﬁll the constraint. The inequation 9 shows a new con-

straint formulation, where the parameter a establishes

the probability of success in the transformation.

min

≤ µ(L

(s)) − aσ(L

(s)) (9)

To explain the meaning of a, we base our reason-

ing in the Chebyshev’s inequality (Canavos, 1984):

P[aσ(L

(s)) ≤ |µ(L

(s)) − L

(p)|] ≤

,∀p ∈ s

where P is the probability function. This inequality is

fulﬁlled for any L

independently of their distribution.

It can be demonstrated that when the new constraint

is fulﬁlled, the probability of failure in the original

constraint is

(Inequation 10).

P[L

(p) ≤ L

min

] ≤

(10)

This result is a probabilistic approach, and as such,

does not guarantees certainty whatsoever. The new

constraint built is a worst case boundary, meaning that

smaller values of a also can provide good results.

5 TEST RESULTS

We built three experiments for solving inverse light-

ing problems. For the ﬁrst one we aim to demonstrate

the use of the variance as a LI. In the second one,

we analyze the method changing statistical parame-

ters for optimization. Those experiments have an av-

erage time execution of 10s for each run, and each

experiment is carried out 20 times, totalizing 200s.

Finally, a performance comparison of the proposed

method with other methods is evaluated. All simu-

lations were performed in a Matlab environment on a

notebook computer (Intel Core i7-2670QM 2.2 Ghz

processor with Turbo Boost up to 3.1 Ghz and 4 GB

DDR3 memory).

Our optimization engine is based on the Vari-

able Neighborhood Search (VNS) method (Hansen

and Mladenovic, 2001). VNS is a single-solution

based metaheuristic that ﬁnds global optimum solu-

tions. However, we believe that similar results could

be achieved with another optimization engine.

5.1 Dispersion

In this experiment we show the use of σ to manage

the distribution of the light in the scene.

Scene: “E” corridor (s

). (n×k)=(24736×1546).

Goal: We seek to illuminate the scene in a uniform

manner, positioning six diffuse light sources.

LI Goal Translation: min σ(L

)).

Constraints Translation: i) Six emitters. ii) Emit-

ters are located in the installation area e (the red-

colored rectangle in Figure 1). iii) The radiosity

value of emitters is unique and predeﬁned.

Variables: 12. Six 2D coordinates that delimit the

location of the light sources.

Running Details: i) The precomputation of Y, V,

and cov(Y), to apply the Eq. 8, takes about 12

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

188

minutes. ii) The VNS algorithm is executed 20

times. iii) 25000 evaluations of σ on each run,

totalizing half a million evaluations.

Results: i) Min, max, and mean of the σ values

found: 0.425, 0.442, and 0.430. ii) Sample image:

Figure 2 (a). Figures 2 (b), (c), and (d) were found

adding to this experiment a constraint (σ ≥ k), and

changing the value of k for each image. Figure 2

(e) was found changing the goal to max σ(L

(s)).

5.2 Statistical Tools for LI

In this experiment we analyze the convenience of us-

ing µ and σ to satisfy a wide variety of LI. The ex-

periment is developed on the same scene and with the

same implementation than the previous one. Four dif-

ferent LI aspects were tested on a speciﬁc wall of the

scene (the “yellow-colored wall” in Figure 1).

Illuminate

Goal: to illuminate the wall as much as possible, po-

sitioning six diffuse light sources.

LI Goal Translation : max µ(L

Y w

)).

Results: Min, max, and mean of the µ values found:

0.394, 0.427, and 0.420. See Figure 4 (a).

Overshadow

Goal: to overshadow the wall as much as possible.

LI Goal Translation: min µ(L

Y w

)).

Results: Min, max, mean of µ values: 7.2×10

−4

7.64×10

−4

, 7.38×10

−4

. See Figure 4 (b).

Disseminate

Goal: to disseminate homogeneously the light over

the wall, within radiosity boundaries.

LI Goal Translation: min σ(L

Y w

)).

LI Constraint Translation: .30≤µ(L

)≤.35.

Results: Min, max, and mean of the σ values found:

0.066, 0.073, and 0.067. See Figure 4 (c).

Contrast

Goal: the highest contrast illumination as possible in

the wall, within radiosity boundaries.

LI Goal Translation: max σ(L

(s)).

LI Constraint Translation: .30≤µ(L

)≤.35.

Results: Min, max, and mean of the σ values found:

0.159, 0.175, and 0.171. See Figure 4 (d).

(a) max µ(=.442) (b) min µ(=7e − 4) (the image

shows L

×50)

.30≤µ(L

)≤.35

(d) max σ(=.175) subject to

.30≤µ(L

)≤.35

Figure 4: Four LI conﬁgurations applied to the “yellow-

colored wall” (see Figure 1).

5.3 Chebyshev-based Constraints

In this experiment we test the new constraint built

(see Ineq. 9), minimizing µ(L

(p)) and replacing

min

=0.1≤L

(p), ∀p ∈“colored-yellow wall” with

min

=0.1≤µ(L

(s))−aσ(L

(s)).

Three values were tested for the parameter a: 1,

2, and 3 (see Figures 5 (a), (b), and (c)). According

to Chebyshev, a = 3 means that less than 1/9 of all

patches have values below 0.1, but the test shows a

better result, because no patch is below the boundary.

5.4 Performance Comparison

The statistical inverse lighting method (SIL) allows

to evaluate half a million µ and σ in less than four

minutes. This result greatly improves previous work.

We compare this result performing the same test with

two different inverse lighting approaches, as used in

(Fern

andez and Besuievsky, 2012): using the full

LRR method and using LRR but computing only the

radiosity at the wall (LRR+) (see Table 1).

StatisticalInverseLighting

189

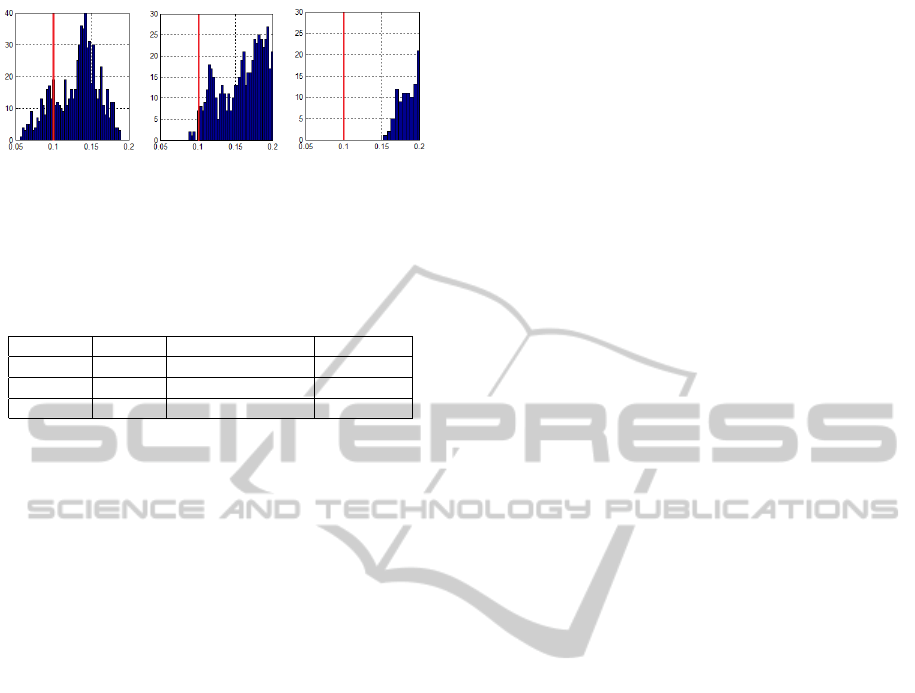
(a) .1 ≤ µ−σ. (µ=.13,

σ=.026).

(b) .1 ≤ µ−2σ. (µ=.17,

σ=.034).

σ=.063).

Figure 5: The LI (minµ(L

(s) subject to .1≤L

) is modeled

with three values of a (from left to right: a=1, 2, and 3).

Table 1: Comparative of optimization approaches against

our statistical technique.

Method Tests/s Total time (min) Speed-Up

SIL 2083 4 -

LRR+ 59 141 35

LRR 8 1041 260

6 CONCLUSIONS AND FUTURE

WORK

In this paper is presented a new methodology for

achieving LI for inverse lighting problems. Our ap-

proach is based on the use of µ and σ as statistical pa-

rameters for the lighting values. Using a low-rank for-

mulation, we demonstrate that µ and σ for L

can be

computed in O(n) and O(n + e

). This result allows

to perform thousands of global illumination evalua-

tion on a desktop PC, reducing drastically the over-

all optimization time required. We believe that this

technique could open a new avenue in the search for

optimal inverse lighting solutions. The results shown

could lead to the use of the method in more complex

scenes with more elaborated lighting intentions. Re-

lated to further development, more effort should be

focus on an automatic parametrization of the LI.

ACKNOWLEDGEMENTS

This work was partially funded by Programa de

Desarrollo de las Ciencias B

asicas (Uruguay) and

by grant TIN2010-20590-C02-02 from Ministerio de

Ciencia e Innovaci

on (Spain).

REFERENCES

Canavos, G. (1984). Applied probability and statistical

methods. Little, Brown.

Cassol, F., Schneider, P. S., Franc¸a, F. H., and Neto, A.

J. S. (2011). Multi-objective optimization as a new

approach to illumination design of interior spaces.

Building and Environment, 46(2):331 – 338.

Castro, F., del Acebo, E., and Sbert, M. (2012). Energy-

saving light positioning using heuristic search. En-

gineering Applications of Artiﬁcial Intelligence,

25(3):566 – 582.

Cohen, M., Wallace, J., and Hanrahan, P. (1993). Radiosity

and realistic image synthesis. Academic Press Profes-

sional, Inc., San Diego, CA, USA.

Contensin, M. (2002). Inverse lighting problem in radiosity.

Inverse Problems in Engineering, 10(2):131–152.

Fern

andez, E. (2009). Low-rank radiosity. In Rodr

ıguez,

O., Ser

on, F., Joan-Arinyo, R., and J. Madeiras,

J. Rodr

ıguez, E. C., editors, Proceedings of the IV

Iberoamerican Symposium in Computer Graphics,

pages 55–62. Sociedad Venezolana de Computaci

aﬁca, DJ Editores, C.A.

Fern

andez, E. and Besuievsky, G. (2012). Inverse lighting

design for interior buildings integrating natural and ar-

tiﬁcial sources. Computers & Graphics, 36(8):1096–

1108.

Fern

andez, E., Ezzatti, P., Nesmachnow, S., and Be-

suievsky, G. (2012). Low-rank radiosity using sparse

matrices. In Proceedings of GRAPP2012, pages 260–

267.

Hansen, P. and Mladenovic, N. (2001). Variable neighbor-

hood search: Principles and applications. European

Journal of Operational Research, 130(3):449–467.

Kawai, J. K., Painter, J. S., and Cohen, M. F. (1993). Ra-

dioptimization - goal based rendering. In ACM SIG-

GRAPH 93, pages 147–154, Anaheim, CA.

Patow, G. and Pueyo, X. (2003). A survey of inverse render-

ing problems. Computer Graphics Forum, 22(4):663–

688.

Russell, S. (2008). The Architecture of Light: Architectural

Lighting Design, Concepts and Techniques: a Text-

book of Procedures and Practices for the Architect,

Interior Designer and Lighting Designer. Concept-

nine.

Russell, S. J. and Norvig, P. (2003). Artiﬁcial Intelligence:

A Modern Approach. Pearson Education, 2 edition.

Schneider, P. S., Mossi, A. C., Franca, F. H. R., de Sousa,

F. L., and da Silva Neto, A. J. (2009). Application of

inverse analysis to illumination design. Inverse Prob-

lems in Science and Engineering, 17(6):737–753.

Schoeneman, C., Dorsey, J., Smits, B., Arvo, J., and Green-

berg, D. (1993). Painting with light. In Proceedings of

the 20th annual conference on Computer graphics and

interactive techniques, ACM SIGGRAPH 93, pages

143–146, New York, NY, USA. ACM.

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

190