A Graph-based Software Tool for the CAD Modeling

of Mechanical Assemblies

Stanislao Patalano

, Ferdinando Vitolo

and Antonio Lanzotti

DiME, University of Naples Federico II, P.le Tecchio 80, Naples, Italy

DIAS, University of Naples Federico II, P.le Tecchio 80, Naples, Italy

Keywords: Mechanical Design, Graph Theory, Digital Pattern, CAD Modeling, Graphical User Interfaces.

Abstract: The challenge of reducing designing time for new mechanical assemblies, especially in the context of large

companies, encourages the use of methods and tools aimed to support designing activities and to re-use the

company know-how. Furthermore, the design choices must be rapidly check to avoid errors that could cause

delay or expensive re-designing. In such a context, the graph theory and related algorithms could be used to

define a transfer function, easily to implement, that governs a software tool able to support the designing

activities. Therefore, the paper presents a designing approach, based on the graph theory, aimed to generate

the geometric modeling of mechanical assemblies. The approach and the software tool are useful both for

designer and companies that want to customize and improve such activities. Finally, the paper shows the

case study related to the design of a transversal manual gearbox and the generation of a GUI, developed in

MatLAB® environment, to validate the approach.

1 INTRODUCTION

In engineering practice, designers often define

mathematical models that describe the behavior of

part or system (mechanical, electrical, naval) under

development. Then, designers provide the

manipulation of a series of equations by using both

the knowledge related to each system and the

relations between mathematical models and physical

reality (Shai and Preiss, 1999). In such context, it is

difficult to individuate each parameter and related

dependencies with the other ones. This is often due

to the large number of equations and parameters that

govern the mechanical or electrical system.

A strategic activity is the reuse of past

experiences during the design phase. The reuse is

often related to the specific designer who has

acquired experiences.

Especially large companies adopt structured

work teams to manage and distribute engineering

knowledge (Sharmin et al., 2009). In such a context,

we believe that software tools aimed to support the

design tasks must adopt Knowledge Based

Engineering (KBE) to capture and reuse knowledge,

in automatic way, during design activities, acquiring

it from each expert designer. In fact, Sandeberg

(2003) define KBE as “the use of advanced software

techniques to capture and re-use product and

process knowledge in an integrated way”. Several

researchers worked on the re-use of product and

process knowledge. Chen et al. (2012) developed a

multi-level assembly model that is useful to capture

the information in different levels of the design

phases. Tang et all (2010) use a design structure

matrix (DSM) method for capture and reuse the past

experience knowledge. In particular, they use

additional tables, linked to DSM, to record

information as type and level of interaction,

milestones and criterions on parameters. This

method requires, however, designer defines

interactions in a subjective way. Therefore, designer

must already have past experiences.

A different approach used especially in the

context of small companies is that the designer must

work and manage all information (as dependencies,

or best cases) in opportune way. This means for the

designer to pour on his skill the success of the

design. Therefore, a concrete contribute to the

growth of small companies is to provide

methodological approach and software tools to adopt

KBE in the above-mentioned way.

During the designing of mechanical parts as

wheels, levers or shafts, after the preliminary sizing

Patalano S., Vitolo F. and Lanzotti A..

A Graph-based Software Tool for the CAD Modeling of Mechanical Assemblies .

DOI: 10.5220/0004299000600069

In Proceedings of the International Conference on Computer Graphics Theory and Applications and International Conference on Information

Visualization Theory and Applications (GRAPP-2013), pages 60-69

ISBN: 978-989-8565-46-4

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

of the part, designers need to verify the correctness

of the hypotheses in use, especially in relation with

multi-objective tasks. In particular, the use of Multi-

Objective Optimization methods induces further

decisions for designers. In fact, designers have to

choose the a priori articulation of preferences i.e.

the specification of parameters, and coefficients

when they are sure about decisions; otherwise, they

have to adopt methods with a posteriori articulation

of preferences when it is difficult to express a

preference before the acquisition of results (Marler

and Arora, 2004). Then, designers build a digital

model by using CAD-CAE environment to deepen

form, function and geometrical characteristics of the

product or to simulate product performances, as

strength or product compliance (Franciosa et al.,

2011).

Therefore, there is a huge need for supporting all

these phases by simplifying and optimizing the

product development process. To meet this need of

integrated knowledge, within CAD-CAE

environment, it is possible to choose additional

knowledge-based modules that make easier the

design tasks for classic and common product (Sham,

2010), (VV. AA., 2008), (VV. AA., 2012). The main

problem of such modules is that they are difficult to

adapt to specific requirements if you are not an

experienced programmer.

If designer do not adapt existing knowledge-

based modules, they have to find different way to

take into account and to represent dependencies

among design parameters.

A very useful tool to rapidly represent the

dependencies among parameters or variables is

provided by the graph theory. Graphs, in fact,

provide the representation of binary relations and

can be used for schematic modeling of many

problems in mathematics, engineering, computer

science, economics, sociology, linguistics, and

wherever it is necessary to represent a binary

correspondence (Deo, 2004), (Franciosa et al.,

2010), (Franciosa et al., 2012).

The way to associate a design methodology to

graph theory could be expressed as follows. In the

axiomatic design, Suh (1990) and (1997) claimed

that is necessary to start from a poor-level of details

for each domain (requirement domain or physical

domain) and to progress using zigzagging technique

between the domains. Using the hierarchical

decomposition, it’s impossible to represent the

dependencies or interactions between the parameters

or elements of product (Tang et al., 2009). With the

use of graph theory it’s possible to create the

directed graph (digraph) that clearly represents the

dependencies between the parameters for any level

of the product hierarchy structure (Deo, 2004).

Therefore, once defined the level of detail it is

possible to associate a digraph for the “transversal”

dependencies in the level. Some authors reserve the

term arc for an oriented or directed edge, while edge

is for undirected edge. In the following we deal with

digraphs, and therefore the term edge will be used to

indicate the oriented edge. For deepening on graph

theory, see (Deo, 2004); (Bondy and Murty, 2008)

and (Wilson, 1978).

The use of graphs has several advantages in

product design:

 to represent all dependencies in a simple and clear

way;

 to increase the level of detail by expanding the

nodes of the graph.

Therefore, the graph representation fits a

common need in designing activities. In fact,

designers first define high-level requirements and

then increase the level of detail by introducing

further parameters and related dependencies among

them.

Some works in literature are aimed to integrate

tools based on graph within CAD systems. In

Franciosa et al. (2009) a tool for a quick checking of

tolerance specifications, directly assigned to a CAD

model, were proposed. Lockett and Guenov (2005)

presented a new approach based on the average area

for a module integrated in CAD feature recognition

and aimed to molded parts. Also during the

generation of CAD models within high-level CAD

environments, as CATIA® or UGS-NX - the last

one added with Wave Engineering module (Sham,

2012), it is possible to explore links between the

assembled parts through graphs.

The present paper proposes an approach and a

software tool to accomplish the geometric modeling

of mechanical assembly by supporting the

preliminary phase of dimensioning as well as the

updating during the re-use of consolidated CAD

models. In particular, the approach allows the

management of company know-how according a

KBE point of view and provides an easy-to use

graphical interface based on directed graphs.

The paper is arranged as follows. Section 2

summarizes the approach to CAD modeling of

assemblies based on graphs. Section 3 and Section 4

provides the application of the approach to the case

of an automotive gearbox and the implemented GUI,

respectively. Finally Section 5 draws conclusions.

AGraph-basedSoftwareToolfortheCADModelingofMechanicalAssemblies

2 THE APPROACH TO CAD

MODELING OF ASSEMBLIES

BASED ON GRAPHS

2.1 General View and Fields of

Intervention

Especially in the context of small or medium

companies, designers are often the main actor in

decision processes, during designing or CAD

modeling activities. The authors here provide an

approach and a software tool first to make automatic

the calculus chains due for the dimensioning and the

locating of assembling parts and then to improve the

re-use of company knowledge related to the

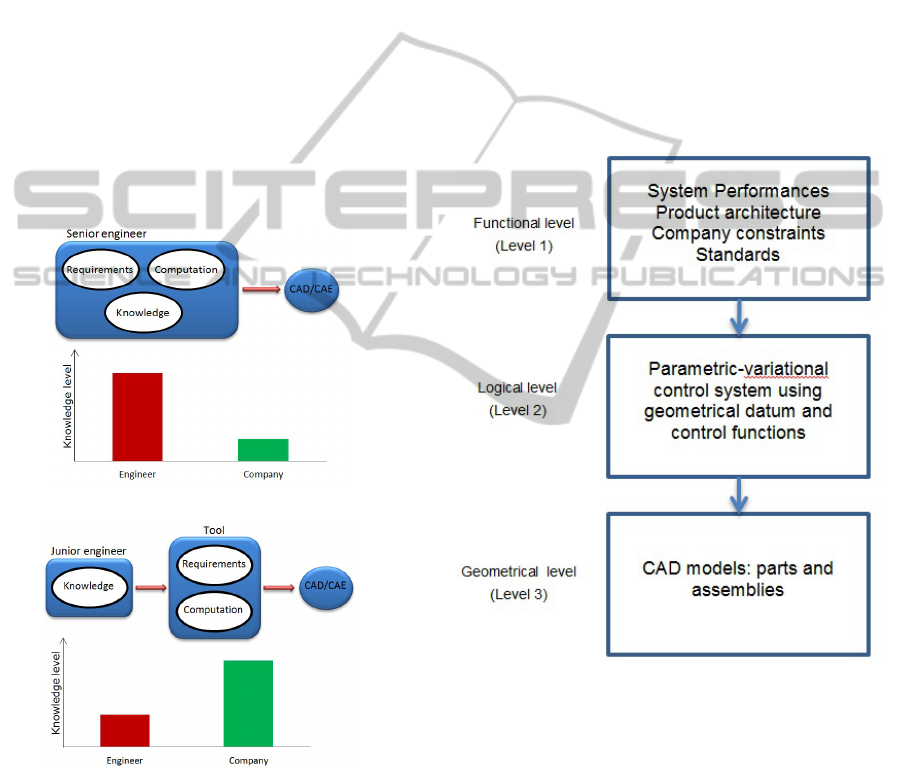
designing activities of different designers (Figure1).

Therefore, also repetitive activities or manual

optimization loops are significantly improved.

Figure 1: a) typical design scheme performed in small-

medium company; b) proposed design scheme.

The proposed approach to CAD modelling deals

with three different levels within the geometric

modelling of assemblies. The three levels are

(Figure 2):

 Functional level (Level 1) where functional groups

are defined; at this level it is possible to operate with

a series of parameters to accomplish the consistency

of functional groups (as for example costs, number

of instances, types of unified components);

 Logical level (Level 2) where datum, parameters

and control rules for dimensions are defined; at this

level it is possible to manage datum or equations to

accomplish geometrical consistency of assembling

parts (curves and surfaces for mating conditions,

axes of rotation, distances between planes as

functional gaps);

 Geometrical level (Level 3) where the geometries

of parts, that compose the assembly, are modeled; at

this level it is possible to operate local changes to

dimensions as well as to further parameters of parts

(thickness and length of parts, curvature’s radii,

Young’s modulus).

Figure 2: Three levels of intervention for the proposed

approach.

The present approach and the developed software

tool allow operating at each of the three levels. In

particular, it is possible to proceed from level 1 to

level 3 for the generation of a new CAD model or,

alternatively, to operate only in one of the three

levels.

The preliminary sizing of an assembly often

imposes to work with a high number of variables

and related equations. Therefore, during this phase it

could be strategic to have a tool that simplify the

management of such equations and makes easily

detectable the dependency of a variable from others.

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

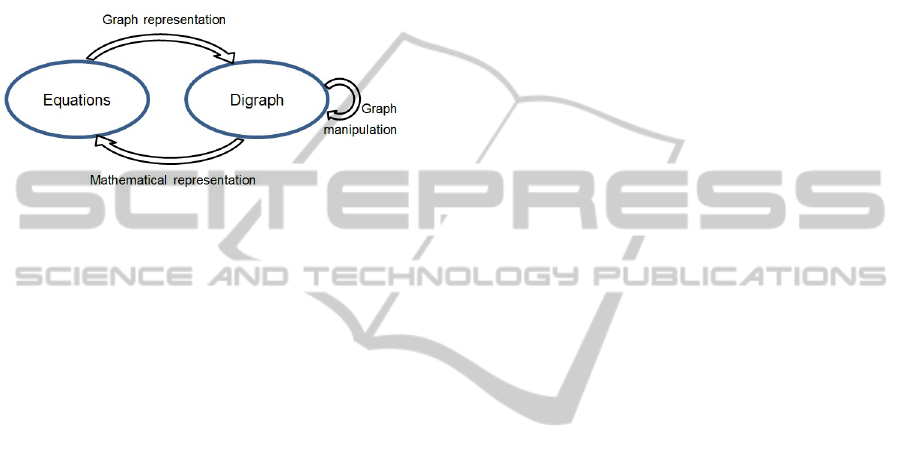
In particular, Shai (2003) claims that is possible to

transform the mathematical problem towards the

graph field and then return with the solution to

mathematical field. The approach presented in this

paper first represents the mathematical and

geometrical relationships by means of graphs; then,

it provides the manipulation of the edges in order to

change the dependencies and, finally, to return to the

mathematical field. This general flow is shown in

Figure 3.

Figure 3: General flow of the proposed approach.

2.2 Approach

The approach to geometric modelling deals with an

editable transfer function based on graphs as

depicted in Figure 4. In particular, the general

transfer function Y is able to correspond (x

, x

,….,

) input parameters to a set of assembly variables

, y

,…., y

) by using parameters, relations and

related computation tasks. At this stage, the set of

relations, representing the dependencies between

parameters, is associated to digraphs. In particular,

the nodes are associated to parameters, while

directed edges represent existing relations. On the

other side, a matrix representation could be used for

software implementation.

Furthermore, the relations represented through

digraphs can be handled generating new transfer

functions. The handling consists of three phases:

 extraction of graphs;

 editing of graphs;

 updating of relations.

2.2.1 Extraction of Graph

The initial set of nodes and relations, assigned by

designers, are represented through digraphs. In

particular, the nodes are arranged in the space by

using the Fruchterman-Reingold’s algorithm as in

(Franciosa, 2009). This algorithm generates the

layout of the graphs according the degree of

attraction or repulsion of nodes. In particular, the

degree of repulsion is a function of the number of

links between the node under consideration and the

surrounding ones linked to the first.

Fully connected graph is the assumption. If the

graph is disconnected and it has several components

the algorithms can be applied to each component.

Before extracting the graph designer is asked to

isolate the input parameters. In fact, these

parameters will be the starting nodes from which to

generate the digraph until to arrive to ending nodes

that represent the outputs i.e. assembly variables.

2.2.2 Editing of Graphs

The phase deals with the editing of digraphs and the

running of algorithms to check validity of the

digraphs. The designer can reverse or delete a link

between two nodes. The possibility to reverse the

direction of the edge, and then of a dependency,

allows to change relationships without

reprogramming the data structure.

When an edge is reversed the algorithm for loop

detection, working on edge list, checks digraphs to

highlight loops to be avoided. In particular, a series

of integers 1,2,….,n is assigned to the vertices.

Starting from the first vertex, the algorithm builds a

directed path P=(



,...,



) until there are no further

vertices linked. Then the algorithm checks if there is

a directed edge from the 



vertex to 



. If there is a

directed edge a circuit is found; if there is no

directed edge, the algorithm deletes 



and checks

for 



. Then it repeats the previous steps until

P=(



), increases 



to next vertex and repeats the

check for the last time. During the execution of steps

a flag vector [1xm] (where m is the number of edges)

could used to record the edges just covered (Deo,

2004).

Similarly, when the edge is removed the

algorithm for isolated node detection (Figure 5),

working on adjacency matrix, verifies if the vertices

adjacent to the removed edge have become isolated.

In particular an edge is defined through two ordered

vertices. Therefore the algorithm detects the adjacent

vertices after the edge removal.

The algorithm proposed in Figure 5 is provided

to analyse throughout the adjacency matrix. In

particular, the vertex under consideration is

indicated with letter “i”, while “j” indicates the node

of interaction. If the cell of adjacency matrix,

identified by them, shows a zero value, it means that

there is no a linked edge between them. If the entire

row “i” has all cells with zero value, i.e.

∑











0, then the vertex is isolated.

AGraph-basedSoftwareToolfortheCADModelingofMechanicalAssemblies

Figure 4: scheme for transfer function and graph

representation.

2.2.3 Updating of Relations

During this phase the relationships between the

parameters are updated. In this way, the editing of

graphs moves to transfer function by means of the

updated relations. The presented approach based on

the above-mentioned three phases (extraction,

editing and updating) implies a series of advantages

for designers. During the generation of initial CAD

models designer is supported when he focuses on

large set of equations and builds related digraph. In

fact, he could easily check, by using the loop

detection algorithm, if there are redundant equations

and he could provide to delete them. Also the

extracting phase supports designer when he locates

the parameters, i.e. the initial nodes of digraphs, as

first member of only one equation to avoid

redundancies.

Then, different designers, who have to operate

changes and consequent regenerations of CAD

models, could operate in an easy and intuitive way

on the digraphs without changing the equations set

out by other colleagues. In other words, it is not

necessary to rewrite one or more equations to

operate changes to transfer function, but it is

sufficient to change the digraph with simple and

intuitive actions.

3 CASE STUDY: GEARBOX

“CMT-6M”

The approach to CAD modelling was applied to the

design and modelling activities due to develop an

automotive manual transverse gearbox with two

shafts and six maximum gears, in the following

called “CMT-6M”. To accomplish the complete

geometrical modelling of the gearbox, the three

levels (functional, logical and geometrical levels)

were carried out.

Figure 5: Algorithm for isolated node detection.

3.1 Functional Level

To accomplish the designing of a family of

gearboxes a set of functional parameters was taken

into account (Table 1), according to know-how of a

European automotive group.

Table 1: Functional parameters.

Materials for

ears

Mat

Materials for shafts

Mat

Costs

umber of shafts

umber of

ears

Teeth Modulus

The bounding volume of the assembly is a

significant requirement in gearbox design as it deals

with the characteristics of layout engine

compartment. Often, similar gearboxes have to be

assembled within different engine compartments and

this induces several changes to the whole

architecture of gearbox as for the dimensions of

gears, the transmission ratios, the distances between

shafts. As same 3D bounding volumes could be

accomplished through different combination of

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

functional or datum parameters, it was not settled as

functional parameters but it was used as inspection

parameter during re-design activities.

3.2 Logical Level

For the sizing of modular toothing the classic theory

for spur gears (Charchut and Thomas 1972) and

(Juvinall and Marshek, 1994) was used. As the

present analysis was not focused to fatigue design,

Lewis' theory together appropriate correction

factors, contained in UNI 8862 standards, for both

nominal and allowable stresses, was used.

Table 2 summarizes the general equations for

gearbox sizing. Table 3 and Table 4 show the

additional equations for straight and helical toothed

sizing, respectively (Appendix A shows notation

used in Table 2, Table 3 and Table 4).

Table 2: General equations for external gears.

Minimum number

of teeth





2

1



1τ



2τ



sin





2τ



sin



Gear ratio









⁄

Tooth width

∗

Pitch diameter





∗

Outside diameter





2

Max size









Table 3: Additional equations to characterize straight-

toothed gears.

Bending





∗





∗



∗



∗





Wear





∗





∗







Table 4: Additional equations to characterize helical-

toothed gears.

Bending





∗





∗



∗



∗



∗





Wear









∗





∗







Number of teeth

dummy











cos







Gear width

∗cos

Furthermore, a set of geometrical datum for the

proper layout of the gearbox elements was

introduced. In particular, to accomplish the

assembling of the manual transverse gearbox with

two shafts and six gears, called “CMT-6M”,

according to a top-down approach, the datum set

depicted in Figure 6 was used. Four axes referred,

respectively, to the primary shaft, the secondary

shaft, the differential gear and the reverse gear

compose the datum set.

The datum set is located by means of four

parameters (Figure 6):

 Axis base primary shaft-idler shaft (



) = distance

between the axis of the primary shaft and the axis of

the reverse idler gear.

 PS-SD angle (



) = angle between the lines that

link the traces of primary-secondary axes and

secondary-differential axes, contained in the plane

perpendicular to such axes;

 Axis base primary-secondary (



) = distance

between the drive axis and the driven shaft;

 Axle base secondary-differential (



) = distance

between the axis of the drive shaft and the axis of

the differential.

3.2.1 Digraph Representation

The parameters and relations defined in functional

and logical levels for each spur gear are translated

into the digraph depicted in Figure 7.

Figure 6: Datum set of the CMT-6M gearbox.

The designer defines all dependencies among

parameters and sets the input in terms of vector of

parameters and list of edges.

The digraph of gearbox (Figure 8) is composed

by a number of subgraphs equal to the number of

spur gear belonging to gearbox. When the gearbox is

AGraph-basedSoftwareToolfortheCADModelingofMechanicalAssemblies

characterized by a different number of gear ratios, it

is possible to add or delete the sub-graph depicted in

Figure 7.

Figure 7: Sub-graph for helical toothed spur gear.

Figure 8: Digraph for CMT-6M gearbox.

3.3 Geometrical Level

Figure 9 depicts the 3D model of CMT-6M gearbox

corresponding to geometrical level. At this level the

independent parameters i.e. the ones that are not

included in the digraph could be updated.

Figure 9: 3D CAD model of CMT-6M gearbox at

geometrical level.

4 CMT-6M GUI

IMPLEMENTATION

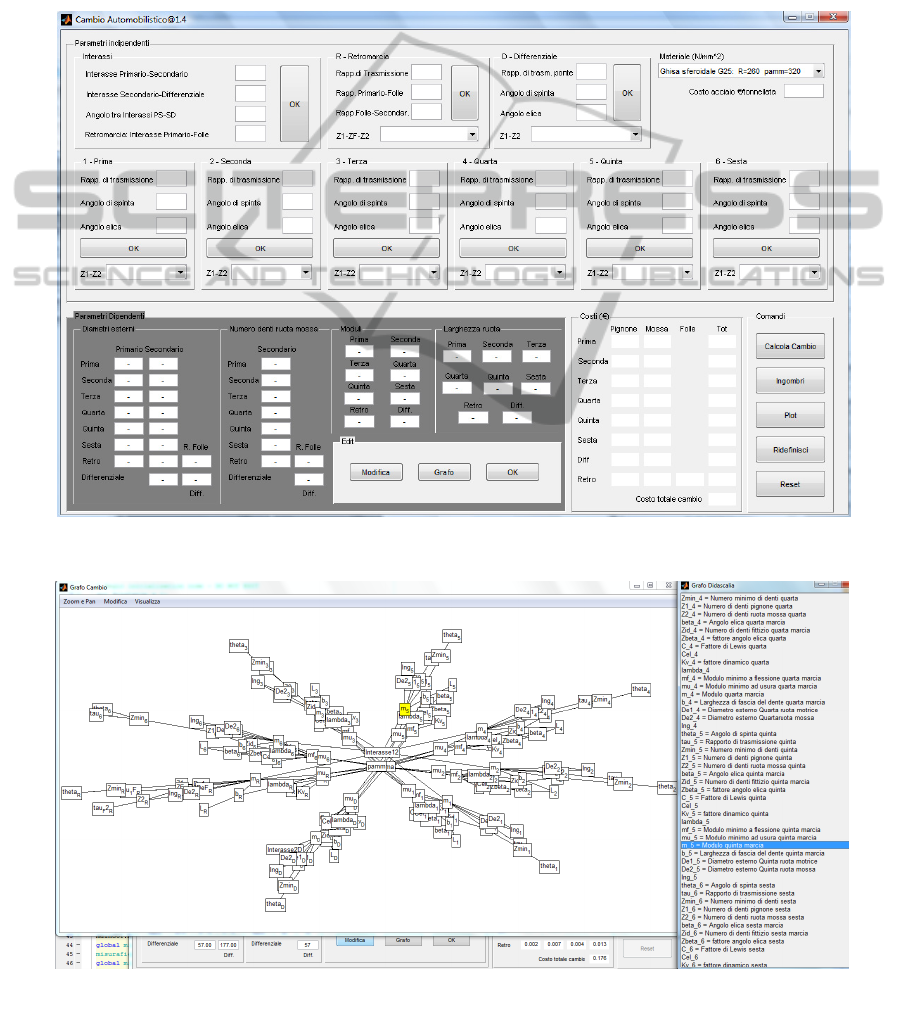
A Graphical User Interface (GUI), developed in

MatLAB environment, was accomplished in order to

support the design of automotive manual transverse

gearboxes (Figure 10). The main window is divided

in two fields: the upper field where the inputs values

of parameters are typed (the field of independent

parameters); the lower field where the output values

are evaluated (the field of dependent parameters).

Furthermore, in the lower field are also located the

keys to provide the editing of generated digraphs

and the evaluation of relations.

The designer can set the number of gears,

belonging to the gearbox, up to a maximum of six.

Figure 11 depicts the digraph of CMT-6M (with

six gears). Using such interface, the designer could

interact within the digraph, by exploring the whole

set of parameters, by modifying the existing links

between nodes and by using the algorithms for loop

detection and for isolated node detection,

respectively. To reduce the computational time,

when designer selects an edge to remove it, (Figure

12) the algorithm for isolated node detection works

only on the two adjacent nodes.

The possibility of

reversing the edge was implemented to convert an

influenced node in a node that influences.

The inversion of a link has to be carefully used

by expert designers. In particular, it should not be

used for a large set of parameters as it causes the

inversion of corresponding relations with

unacceptable consequences.

Otherwise, the deleting of an edge from digraph

determines the elimination of dependence in the

corresponding equation. So, the father-child relation

that link two adjacent nodes is deleted. Designer can

interactively deletes a link between two nodes when

the corresponding relation is negligible.

When all links associated to a node are deleted,

the corresponding parameter becomes

“independent”. Therefore, the deleting of links is

useful for nodes located at the end of digraph chains

i.e. for nodes that have no outgoing edges. In fact, in

such case the deleted edge does not cause

unpredictable effects to the design process but it

allows setting a value to a parameter that is

independent from the calculated one. An example is

the gear width parameter (



 in the sub-graph

for helical toothed spur gear (Figure 7). As the node

has not outgoing edges, the designer could

disconnect this node (see Figure 12) and provide a

new input value, keeping the geometrical correctness

of the toothing.

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

The computational results are currently displayed

in a dedicated environment. By clicking on “Plot”

command, the characteristic surfaces of toothing i.e.

head, sides and foot of helical-toothed gears are

displayed on screen (Figure 13). In this environment

is also possible to change the mesh degree (Figure

14) to accomplish the desired accuracy of

geometries. Then, it is possible to export the points

of meshes, related to the geometry of whole

assembly, by using a text format

to generate the 3D model in any CAD environment.

The designer could also evaluate the bounding

volumes of CAD models. In a separate window

(Figure 15), in fact, it is possible to evaluate the

distances between two points along different

directions and, then, to easily assign different input

values to functional or datum parameters to fit, after

the automatic re-generation of geometries the

desired bounding volume.

Figure 10: GUI for CMT-6M gearbox.

Figure 11: Automatic generation of gearbox digraph (left). Legend of digraph (right).

AGraph-basedSoftwareToolfortheCADModelingofMechanicalAssemblies

Figure 12: The second command of the node context

menu, allows removing edge.

Figure 13: Environment for display of the surfaces.

Figure 14: a) minimum degree mesh: 2 elements for edge;

b) maximum degree mesh: 50 elements for edge.

5 CONCLUSIONS

The paper presents an approach, based on the graph

theory, aimed to generate the geometric modeling of

mechanical assemblies.

The approach focuses on the management and

re-using of company know-how, according to a KBE

point of view.

The developed GUI enables designers to

interactively and easily generate several instances of

geometrical models by acting on a digraph

representation instead of operating on a large set of

equations and parameters.

Figure 15: Environment for bounding volume evaluation.

The introduction of such a GUI implies both

significant times for its setting up and costs due to

the training of designers. Nevertheless, the use of

GUI contributes to the reduction of time to market of

new gearboxes, enriches the company know-how,

improves the sharing of knowledge between

designers and facilitates the division of tasks

between designers with different designing

experiences. A possible scenario in using such GUI

is that “expert designers” could use digraph

representation to share knowledge, to add relations

among parameters and, more generally, to change in

an interactive way, complex transfer functions that

control dependent design parameters. Otherwise,

“younger designers” could accomplish the

requirements related to the overall volume of

gearbox by modelling different configurations of

gears.

The GUI is actually not embedded in a specific

CAD environment to give the possibility to export

results towards any CAD environment. In fact, the

GUI exports data as a cloud of points assuring an

effective integration within the company CAD

systems in use.

Further developments, concerning with the GUI

definition, will deal with the integration of the GUI

in a CAD environment to optimise the generation of

CAD models; moreover, the setting up of

dependencies among graph nodes will be

accomplished in a fully automatic way starting from

the existing equations. Finally, different case studies

dealing with partially known transfer functions will

be taken into account.

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

ACKNOWLEDGEMENTS

The present paper was developed with the economic

support of MIUR (Italian Ministry of University and

Research) performing the activities of the project

PON01_01268 “Digital pattern product

development: a pattern driven approach for

industrial product design”.

REFERENCES

Bondy, J. A., Murty U. S. R., 2008. Graph theory,

Springer. New Delphi.

Charchut, W., Thomas, A. K., 1972. Ingranaggi, Tecniche

Nuove. Milano.

Chen, X., Gao, S., Yang, Y., Zhang, S., 2012. Multi-level

assembly model for top-down design of mechanical

products. Computer Added Design, vol. 44, pp. 1033-

1048.

Deo, N., 2004. Graph theory with applications to

engineering and computer science, PHI Learning.

New Delphi.

Franciosa, P., 2009. Modeling and simulation of

variational rigid and compliant assembly for tolerance

analysis, PhD Thesis. Naples.

Franciosa, P., Patalano, S., Riviere, A., 2010. 3D tolerance

specification: an approach for the analysis of the

global consistency based on graphs. International

Journal of Interactive Design and Manufacturing, vol.

4 (1), pp. 1-10.

Franciosa P., Gerbino S., Patalano, S., 2011. Simulation of

Variational Compliant Assemblies with Shape Errors

Based on Morphing Mesh Approach, Int. Journal of

Advanced Manufacturing Technology, vol. 53,

Numbers 1-4, pp.47-61, ISSN 0268-3768.

Franciosa P., Gerbino S., Lanzotti A, Patalano S., 2012.

Automatic evaluation of variational parameters for

tolerance analysis of rigid parts based on graphs,

International Journal of Interactive Design and

Manufacturing, ISSN 1955-2513, Springer Paris, DOI

10.1007/s12008-012-0178-4.

Juvinall, R. C., Marshek, K. M., 1994. Fondamenti della

progettazione dei componenti delle macchine, ETS.

Lockett, H. L., Guenov, M. D., 2005. Graph-based feature

recognition for injection moulding based on a mid-

surface approach. Computer-Aided Design, vol. 37,

pp. 251-262.

Marler, R. T., Arora, J. S., 2004. Survey of multi-objective

optimization methods for engineering. Structural and

multidisciplinary optimization vol. 26 (6), pp. 369-

395.

Sandeberg, M, 2003. Knowledge based engineering – in

product development. ISSN: 1402-1536.

Shai, O., 2003. Transforming engineering problems

through graph representations. Advanced Engineering

Informatics, vol. 17, pp. 73-93.

Shai, O., Preiss, K., 1999. Graph theory representations of

engineering systems and their embedded knowledge.

Artificial Intelligence in Engineering, vol. 13, pp.

273–285.

Sham Tickoo, 2010. CATIA V5R19 for engineers and

designers, Dreamtech Press.

Sham Tickoo, 2012. NX8 for designers, CADCIM

Technologies.

Sharmin, M., Bailey, B. P., Coats, C., Hamilton, K., 2009.

Understanding knowledge management practices for

early design activity and its implications for reuse.

CHI 2009 Proceedings of the 27

international

conference on human factors in computing systems,

pp.2367-2376.

Suh, N. P., 1990. The principles of design. Oxford

University Press. New York.

Suh, N. P., 1997. Design of Systems. Annals of the CIRP,

vol. 46 (1), pp. 75-80.

Tang, D., Zhang, G., Dai, S., 2009. Design as integration

of axiomatic design and design structure matrix.

Robotics and Computer-Integrated Manufacturing,

vol. 25, pp. 610-619.

Tang, D., Zhu, R., Tang, J., Xu, R., He, R., 2010. Product

design knowledge management based on design

structure matrix. Advanced Engineering Informatics,

vol. 24, pp. 159-166.

VV.AA., 2008. CATIA - Product Knowledge Template

Definition 2, Dassault Systemes. www.3ds.com/

product/catia.

VV.AA., 2012. Data sheet CREO Advanced Assembly

Extension, PTC Inc.

Wilson, R. J., 1978. Introduzione alla teoria dei grafi,

Cremonese Editore.

APPENDIX A - NOTATION

Below are listed the parameters shown in Table 2,

Table 3 and Table 4:

 = transverse pressure angle;





= number of teeth on driven gear;





= number of teeth on drive gear;

 = helix angle;

 = module;

 = face factor;

 = Lewis’s geometric factor;





= 0.830.88∗ for 15°30°;

 = torque;





= allowable stress;





= allowable pressure;





= dynamic factor;





= helix angle factor.

AGraph-basedSoftwareToolfortheCADModelingofMechanicalAssemblies