
Keypoints Detection in RGB-D Space
A Hybrid Approach
Nizar Sallem
1
, Michel Devy
1
, Suat Gedikili
2
and Radu Rusu
3
1
LAAS-CNRS, Universit
´
e de Toulouse, Toulouse, France
2
Willow Garage, Menlo Park, CA, U.S.A.
3
Open Perception, Menlo Park, CA, U.S.A
Keywords:
Keypoints, Corner, Detection, RGB-D.
Abstract:
Features detection is an important technique of image processing which aim is to find a subset, often dis-
crete, of a query image satisfying uniqueness and discrimination criteria so that an image can be abstracted
to the computed features. Detected features are then used in video indexing, registration, object and scene
reconstruction, structure from motion, etc. In this article we discuss the definition and implementation of such
features in the RGB-Depth space RGB-D. We focus on the corners as they are the most used features in image
processing. We show the advantage of using 3D data over image only techniques and the power of combining
geometric and colorimetric information to find corners in a scene.
1 INTRODUCTION
Corner detection in images can be traced back to
Moravec (Moravec, 1981) who used small pixel
neighborhood (patches) to define a region of an image
as an edge or a corner comparing it to its surrounding
regions. Followed by Harris and Stephens, Plessy and
Shi-Tomasi who overcome the slowness of Moravec’s
detector using the image’s second moment matrix to
account for intensity direction change and thus cor-
ner presence. A considerable amount of work was
achieved toward invariance in scale and affine trans-
formation leading to robust features A detailed re-
view of keypoint detectors can be found in (Tuytelaars
and Mikolajczyk, 2008) and (Li and Allinson, 2008).
When they rely on intensity changes, corners behave
poorly in texture-less environment and bad light con-
ditions. Geometric data, on the other hand is not sen-
sitive to such arguments, and a geometric based cor-
ner detector should behave equally regardless to the
presence or absence of texture under different light
conditions. We propose an extension to popular im-
age corner detector where we account for geometric
changes to define the cornerness measure that we en-
hance further by integrating intensity information.
Detecting corners in a 3D point cloud is a chal-
lenging, relatively new topic in computer vision. In
(Sipiran and Bustos, 2011) authors address the prob-
lem of detecting corners in a 3D mesh. They exploit
the mesh connectivity for local information and use
PCA to tear down the problem and exploit directly
the 2D algorithm in (Harris and Stephens, 1988). In
(Knopp et al., 2010) and (Redondo-Cabrera et al.,
2012), authors detect 3D SURF corners exploiting
mesh and voxel grid. They first voxelize the shape
into a 256
3
voxel grid using faces intersection with
grid edges then they apply the algorithm in (Bay et al.,
2006) accounting for one additional dimension.
Compared to these work we also address the prob-
lem of finding corners in 3D but we choose to rely
also on geometric data to discriminate corners from
regular points not only intensity as in all the above
mentioned references. An additional difference with
(Sipiran and Bustos, 2011) and (Knopp et al., 2010)
is that we perform detection on the points at an ear-
lier stage of the acquisition pipeline with no shape
nor mesh information which saves time and resources.
Furthermore, we don’t require voxelization which is
an expensive technique and rely solely on local infor-
mation.
In section 2 we extend intensity based corners to
3D. Combination of geometric and color criteria is
done in 3. The results of novel detectors are the sub-
ject of the evaluation in 4.
496
Sallem N., Devy M., Rusu R. and Gedikili S..
Keypoints Detection in RGB-D Space - A Hybrid Approach.
DOI: 10.5220/0004305004960499
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 496-499
ISBN: 978-989-8565-47-1
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Normal direction at different point locations
within its local neighborhood (green circle). a. point on
a plane b. point on an edge c. point on a corner.
2 CORNER DETECTION IN 3D
Observation of the normals at 3D points locations lead
to:
1. if point (p
0
, ~n
0
) is on a plane then all the normals
~n
i
in a sufficiently small neighborhood are paral-
lel;
2. if point (p
0
, ~n
0
) is on an edge e, the neighborhood
is divided on three distinct groups: points on the
edge share same normal direction as ~n
0
and points
on both sides of e have respectively two directions
∆
+
and ∆
−
;
3. if point is a corner or an isolated point then imme-
diate neighbors would have distinct normals di-
rections.
These situations are illustrated on Figure 1. Variation
in normals directions appears to be a good indicator
on corner presence. We can separate the detectors in
two families according to how it is computed: second
order moments and self discriminality.
2.1 Self Dissimilarity Detectors
A natural way to compute the variation is to account
the differences between the central pixel, nucleus,
value and its neighbors. Smallest Univalue Segment
Assimilating Nucleus (SUSAN) (Smith and Brady,
1995) and Minimum Intensity Change (MIC) (Tra-
jkovic and Hedley, 1998) detectors rely on this prin-
ciple in a more elaborated way to find corners on an
image. When dealing with normals the angle formed
by normals direction is a good indicator on normals
differences.
For the extended SUSAN version, a spherical
mask M is placed on the nucleus n and
∀p ∈ M,c(p) = N(p).N(n) (1)
Then M
c
is computed as
M
c
(n) =
(
g − A(n) = g −
∑
p∈M
c(p), A(n) < g
0 else
(2)
The extended MIC on the other hand is stated as:
∀p ∈ M,c(p) = (N(p).N(n))
2
+ (N(p
0
).N(n))
2
(3)
where (p, p
0
) are diametrically opposed with respect
to n. Then
M
c
(n) = min
p∈M
(c(p)) (4)
2.2 Second Order Moments Matrix
Detectors
Consider a point cloud P with normals N, the sum S
of the squared differences of a patch around region
defined by (u,v, w) of P shifted by an amount (x,y,z)
is given in Equation 5. We exploit Taylor’s expan-
sion as in (Harris and Stephens, 1988): N(u + x,v +
y,w + z) ≈ N(u,v,w) + N
x
(u,v,w)x + N
y
(u,v,w)y +
N
z
(u,v,w)z where N
x
, N
y
and N
z
, respectively, are the
components along X Y and Z axis of normal N.
A in Equation 5 corresponds to normals covari-
ance matrix and its eigenvalues (λ
1
,λ
2
,λ
3
) analysis
offers a clear indication on the direction of variations.
• Harris: M
c
= λ
1
λ
2
λ
3
− κ(λ
1
+ λ
2
+ λ
3
)
2
=
det(A) − κtrace
2
(A), κ a tunable parameter;
• Shi-Thomasi: M
c
= min(λ
1
,λ
2
,λ
3
);
• Noble: M
c
= det(A)/trace(A);
• Lowe: M
c
= det(A)/(trace(A))
2
.
3 HYBRID DETECTION IN
RGB-D
From the observations in Section 2, a problem shows
up concerning the proposed algorithms when dealing
with superposed planar objects or coplanar planar ob-
jects. Indeed, since the normals are parallel no differ-
ence can be computed so no corners will be detected.
We can take advantage of the RGB-D sensors to dis-
criminate corners either according to geometric crite-
rion when they are located on different planes even
if they have the same intensity value or with help of
intensity if they have different textures.
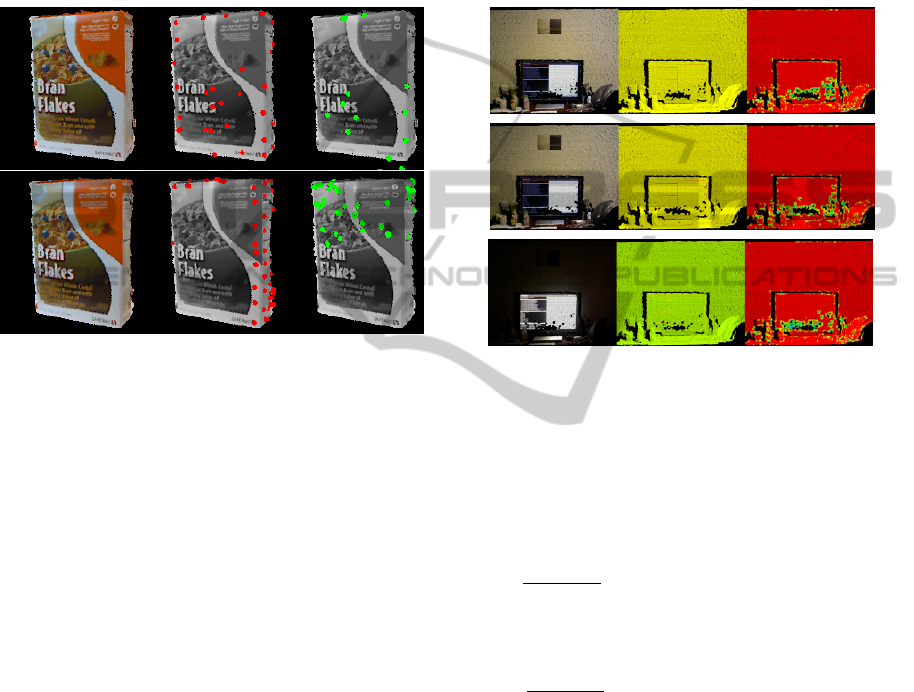
Detection result on some objects in the RGB-D
dataset(Lai et al., 2011) are shown in the Figure 2 and
. Note that due to the working range of the camera,
some point clouds are too small to be displayed. We
used Lowe response and a search radius of 0.10 m.
We show 3D keypoints and hybrid ones to show dif-
ference in location. Same search radius 0.01 m is used
for both hybrid and 3D detection.
KeypointsDetectioninRGB-DSpace-AHybridApproach
497
S (x, y, z) =
∑
uvw
h
α
uvw
[N(u + x, v + y,w +z)−N(u,v, w)]
2
.N(u + x, v + y,w +z)
i
≈
x y z
∑
uvw
α
uvw
N
2
x
N
x
N
y
N
x
N
z
N
y
N
x
N
2
y
N
y
N
z
N
z
N
x
N
z
N
y
N
2
z
x
y
z
≈
x y z
A
x
y
z
(5)
Figure 2: Hybrid keypoints on cereal boxes from the RGB-
D dataset. 3D keypoints are displayed with red spheres,
hybrid keypoints are displayed with green spheres. Notice
that the red spheres location is different from the green ones
due to the added intensity variation. First row corresponds
to Harris detectors and second row to SUSAN detectors.
4 EXPERIMENTAL RESULTS
Two major limitations of the classic corner detector
we address are the light conditions and the absence of
texture. In here, we evaluate performance of the ge-
ometric or 3D corner detector in such situations. To
achieve a fair comparison we use a RGB-D sensor that
outputs 3D and images data. Geometric detectors are
evaluated against their images homologous in differ-
ent illumination and texture conditions.
4.1 Light Invariance
For this experiment we take 3 images of the same
scene with different lighting conditions. We compare
corners detection with Harris method on the 3D point
cloud and the image. As shown on the Figure 3, 3D
corners are more stable to light conditions.
Repeatability of the detectors can be evaluated for
the above mentioned dataset by comparing the 3D re-
sponses:
Figure 3: Geometric detectors evaluation: light invariance.
Scene images (left column) were acquired using an Asus
Xtion PRO LIVE RGB-D camera. Image corners detec-
tion (middle column) was performed using a window of
size 3x3. Geometric corners detection (right column) was
performed using a radius 0.015m. Cornerness is displayed
from red (low) to green (high). The 2D response fades as
the light is dimmed.
¯
ε
3D
=
∑
p
i
δ
3D
(p
i
)
card(P
1
)
,δ
3D
(p
i
) = M
c
(P
1
(p
i
))− M
c
(P
2
(p
i
))
and 2D ones:
¯
ε
2D
=
∑
p
i
δ
2D
(p
i
)
card(I
1
)
,δ
2D
(p
i
) = M
c
(I
1
(p
i
)) − M
c
(I
2
(p
i
))
for all available pairs.
¯
ε
3D
is the 3D repeatability
mean error of standard deviation σ
3D
and its coun-
terpart
¯
ε
2D
of standard deviation σ
2D
.
¯
ε
3D
= 0 which
proves the stability of the 3D corner detector in strong
light variation while
¯
ε
2D
varies significantly. Table 1
sums up these results.
4.2 Texture Invariance
To evaluate the performance of the 3D corners on
texture, we acquired a data set of objects with simi-
lar shapes but carrying different textures (text, colors,
pictures). We measure the cornerness using intensity
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
498

Table 1: Corners repeatability mean and standard error de-
viation in strong light variation for 2D and 3D Harris corner
detectors. P
i
1≤i≤3
are the input clouds. The mean error
¯
ε
2D
high values show how light affects 2D corners.
pairs P
1
− P
2
P
1
− P
3
P
2
− P
3
¯
ε
2D
177034 695510 698783
¯
ε
3D
0 0 0
σ
2D
1.54e + 06 5.42e + 06 5.81e + 06
σ
3D
0 0 0
Figure 4: Geometric corners detection: texture invariance.
Cornerness is displayed from green (weak) to red (strong).
3D cornerness - right column - is almost the same for all the
objects although they carry different textures while 2D cor-
nerness - middle column - varies according to the texture.
and normals. Detection results (non filtered) are pre-
sented in Figure 4.
The results shown on Figure 4, confirm our intu-
ition: since we rely solely on geometric data varia-
tion for this experiment, objects of the same shape
should have similar signature. Lecturers can easily
notice that 3D cornerness measure is analogous for
the whole 3
rd
column while it differs depending on
the object texture along the 2
nd
column.
5 CONCLUSIONS
This paper addresses the problem of corner detection
in RGB-D space to improve repeatability under strong
light variation or in texture-less environments. The
novelty of the proposed solution is the use of a geo-
metric criterion to assess the nature of a point. The
novel detectors are extension of popular 2D images
corner detectors: second moment matrix and self dis-
criminality ones.We prove stability of designed de-
tectors through experimental validation. Future work
include application to point cloud registration, object
recognition and tracking.
ACKNOWLEDGMENTS
This work has been supported both by the French na-
tional research agency (ANR) by the project ANR As-
sist ANR-07-ROBO-0011, and by the Willow Garage
company, Menlo Park, California, USA.
REFERENCES
Bay, H., Tuytelaars, T., and Van Gool, L. (2006). Surf:
Speeded up robust features. pages 404–417.
Harris, C. and Stephens, M. (1988). A combined corner and
edge detection. In Proceedings of The Fourth Alvey
Vision Conference, pages 147–151.
Knopp, J., Prasad, M., Willems, G., Timofte, R., and
Van Gool, L. (2010). Hough transform and 3d surf for
robust three dimensional classification. In Proceed-
ings of the 11th European conference on Computer vi-
sion: Part VI, ECCV’10, pages 589–602, Berlin, Hei-
delberg. Springer-Verlag.
Lai, K., Bo, L., Ren, X., and Fox, D. (2011). A large-
scale hierarchical multi-view RGB-D object dataset.
In ICRA, pages 1817–1824. IEEE.
Li, J. and Allinson, N. M. (2008). A comprehensive review
of current local features for computer vision. Neuro-
comput., 71(10-12):1771–1787.
Moravec, H. P. (1981). 3d graphics and the wave theory. In
SIGGRAPH ’81: Proceedings of the 8th annual con-
ference on Computer graphics and interactive tech-
niques, pages 289–296, New York, NY, USA. ACM.
Redondo-Cabrera, C., Lopez-Sastre, R. J., Acevedo-
Rodriguez, J., and Maldonado-Bascon, S. (2012).
SURFing the point clouds: Selective 3D spatial pyra-
mids for category-level object recognition. In IEEE
CVPR.
Sipiran, I. and Bustos, B. (2011). Harris 3d: a robust exten-
sion of the harris operator for interest point detection
on 3d meshes. Vis. Comput., 27(11):963–976.
Smith, S. M. and Brady, J. M. (1995). Susan - a new ap-
proach to low level image processing. International
Journal of Computer Vision, 23:45–78.
Trajkovic, M. and Hedley, M. (1998). Fast corner detection.
Image Vision Comput., 16(2):75–87.
Tuytelaars, T. and Mikolajczyk, K. (2008). Local invariant
feature detectors: a survey. Found. Trends. Comput.
Graph. Vis., 3(3):177–280.
KeypointsDetectioninRGB-DSpace-AHybridApproach
499
