
Spatially Varying Blur Recovery
Diagonal Approximations in the Wavelet Domain
Paul Escande
1
, Pierre Weiss
1
and Franc¸ois Malgouyres
2
1
ITAV-UMS3039, Universit
´
e de Toulouse, CNRS, Toulouse, France
2
IMT-UMR5219, Universit
´
e de Toulouse, CNRS, Toulouse, France
Keywords:
Image Deblurring, Spatially Varying Blur, Operator Approximation, Wavelet Packet Transform, Bi-harmonic
Spline Interpolation, Convex Optimization.
Abstract:
Restoration of images degraded by spatially varying blurs is an issue of increasing importance. Many new
optical systems allow to know the system point spread function at some random locations, by using micro-
scopic luminescent structures. Given a set of impulse responses, we propose a fast and efficient algorithm to
reconstruct the blurring operator in the whole image domain. Our method consists in finding an approximation
of the integral operator by operators diagonal in the wavelet domain. Interestingly, this method complexity
scales linearly with the image size. It is thus applicable to large 3D problems. We show that this approach
might outperform previously proposed strategies such as linear interpolations (Nagy and O’Leary, 1998) or
separable approximations (Zhang et al., 2007). We provide various theoretical and numerical results in order
to justify the proposed methods.
1 INTRODUCTION
Image restoration in the presence of spatially varying
blur is a problem of increasing importance. It was first
studied in the context of satellite imaging with Hubble
space telescope (Nagy and O’Leary, 1998). It is now
becoming increasingly important with the emergence
of new fluorescence microscopes, producing highly
deteriorated images, since light interacts with the bi-
ological tissues. In microscopy, it is often possible
to incorporate micro-beads in the medium surround-
ing the sample or even in the sample itself, giving ac-
cess to the point spread function (PSF) of the system
at some known locations (see e.g. (Preibisch et al.,
2010; Temerinac-Ott et al., 2011)). This information
allows to interpolate the PSF in the whole space and
thus to get approximations of the degradation opera-
tor for further processing.
In the case of spatially invariant blur, fast decon-
volution algorithms can be devised since the convo-
lution is diagonal in the Fourier domain. This allows
using O(dn
d
log(n)) algorithms (where d denotes the
space dimension and n
d
denotes the number of pix-
els) based on the fast Fourier transform. These ap-
proaches are unsuitable in the case of spatially vary-
ing blurs and it appeals for the development of new
fast numerical algorithms. Our aim in this paper is to
propose fast O(n
d
) algorithms based on the wavelet
or wavelet packet transforms.
We consider a blurring operator H in R
d
and de-
fined for any u ∈ L
2
(Ω) as the following integral op-
erator:
∀x ∈ Ω, (Hu)(x) :=
Z
y∈Ω
K(x, y)u(y)dy, (1)
where Ω ⊆ R
d
is the image domain. The function
K(x, ·) is a spatially varying kernel defining the PSF
at each location x. In all the following, we assume that
H is a bounded linear operator from L
2
(Ω) to L
2
(Ω).
The most naive approach to compute Hu numerically
consists in discretizing (1) by:
∀x ∈ X, Hu(x) =
∑
y∈X
K(x, y)u(y),
where X ⊂Ω denotes the set of pixels locations. This
approach is simple to implement, but costs O(n
2d
)
arithmetic operations. This is unsuitable for large 2D
images or medium sized 3D images. Two alternative
approaches are commonly used:
• The first one consists in approximating K(x, ·) by
a tensor product of kind:
K(x, (y
1
, ··· , y
d
)) =
d
∏
k=1
K
k
(x, y
k
).
222
Escande P., Weiss P. and Malgouyres F. (2013).
Spatially Varying Blur Recovery - Diagonal Approximations in the Wavelet Domain.
In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 222-228
DOI: 10.5220/0004308202220228
Copyright
c
SciTePress

Figure 1: An orthogonal view of a Variable Refractive Gib-
son and Lanni PSF obtained with the PSF Generator plugin
for ImageJ (Kirshner et al., 2011).
This reduces the computational cost to O(dn
d+1
)
operations which is usually tractable even in large
scale scenarii. Moreover this model is exact for
Gaussian PSF which sometimes accurately de-
scribe perfect microscopy systems (Zhang et al.,
2007). Unfortunately, it is too rough to describe
more complex patterns commonly encountered
in optical diffraction or sample induced degrada-
tions. Figure 1 shows a typical PSF in three di-
mensions, which cannot be approximated by sep-
arable functions.
• The second one consists in using piecewise con-
stant blurs using local FFT (Nagy and O’Leary,
1998; Hansen et al., 2006). Its complexity is
roughly the same as that of spatially invariant
blurs in O(dn
d
log(n)). Moreover, this approach
also allows to use linear interpolations of the PSF.
This might be interesting in our case since the PSF
is known only at a few positions and linear in-
terpolations allow an operator reconstruction on
the whole image domain. Unfortunately, piece-
wise constant blurs or linear interpolations are too
rough to describe some practical settings. This is
illustrated on Figure 8(b), where we can observe
that the linear interpolation gives a cross like PSF
in the middle, that would be undesirable in practi-
cal cases.
In this work, we propose to approximate H by op-
erators diagonal in wavelet or wavelet packet trans-
forms. More precisely, we show that H ' ΨΣΨ
∗
,
where Ψ denotes the wavelet transform and Σ is a di-
agonal matrix. The computation of Hu is thus reduced
to O(n
d
) operations.
The structure of the paper is as follows. In section
3, we justify the use of such a structure by theoretical
and numerical results. In section 4, we propose an
algorithm to reconstruct the diagonal operator Σ when
the impulse response of H is given at some known
locations.
2 NOTATION
In order to simplify the notation, we consider wavelet
transforms and not wavelet packet transforms. We
present the theoretical results in 1D for the sake of
simplicity and clarity and the experimental results in
2D. The proposed approaches can be extended to any
dimensions and would be particularly suited to large
3D problems.
We consider an orthogonal wavelet basis of
L
2
(R ):
{φ
l
0
,n
}
n∈Z
∪{ψ
j,n
}
j≤l
0
,n∈Z
,
where
ψ
j,n
(t) =
√
2
−j
ψ(2
−j
t −n), (2)
and ψ is the mother wavelet. The function φ
l
0
,n
is
defined by
φ
l
0
,n
(t) =
√
2
−l
0
φ(2
−l
0
t −n),
where φ is the scaling function.
In all the paper, Ψ
∗
denotes the forward wavelet
transform and Ψ denotes its inverse (in the discrete
and in the continuous setting). F
∗
denotes the Fourier
transform (discrete or continuous) and F denotes its
inverse. The convolution between u and h is denoted
h ? u. The Fourier transform of u is denoted ˆu or F
∗
u
For a discrete image in R
d
, we define the discrete
partial derivative in direction i by:
∂
i
u(·, k, ·) =
u(·, k + 1, ·) −u(·, k, ·) if 1 ≤k < n
0 if k = n.
where the indice k is that the i-th position in the array.
The discrete gradient operator in R
d
is defined by:
∇ = (∂
1
;∂
2
;··· ; ∂
d
)
Let q ∈ (R
n
d
)
d
represent a discrete vector field. We
set
q = (q
1
;q
2
;··· ; q
d
).
The isotropic l
1
-norm in (R
n
d
)
d
is defined by:
kqk
1,2
=
n
d
∑
i=1
v
u
u
t
d
∑
j=1
q
j
(i)
2
.
Finally, the discrete total variation of u ∈ R
n
d
is de-
fined by:
TV (u) = k∇uk
1,2
.
SpatiallyVaryingBlurRecovery-DiagonalApproximationsintheWaveletDomain
223

3 DIAGONALIZATION OF THE
VARIABLE BLUR OPERATOR
IN A WAVELET BASIS
The main ingredient allowing the design of efficient
deconvolution algorithms is the fact that a convolu-
tion is diagonalized in the Fourier domain. For any
kernel h, h ? u = F ΣF
∗
u where Σ can be considered
as a diagonal operator that multiplies F
∗
u by F
∗
h.
The main idea of this paper is to mimic this property
for spatially varying blur operators. We propose to ap-
proximate H by an operator
˜
H diagonal in the wavelet
domain:
Hu '
˜
Hu
:= ΨΣΨ
∗
u
=
∑
n∈Z
hφ
l
0
,n
, uiφ
l
0
,n
+
∑
j≤l
0
,n∈Z
σ
j,n
hψ
j,n
, uiψ
j,n
where (σ
j,n
)
j,n
is a sequence of weights that will be
described later. This particular structure allows to ap-
proximate Hu in O(n
d
) arithmetic operations, which
is doable even for very large scale problems.
Such operators have been deeply analyzed from a
theoretical point of view in various articles or mono-
graphs (see e.g. (Beylkin et al., 1991; Coifman and
Meyer, 1997)). However, we found very few im-
age processing applications in the literature. To our
knowledge, the closest practical application is ded-
icated to the fast computation of image foveation
(Chang et al., 1999). However, this work is only
adapted to very particular kind of kernels K met in
foveation that do not correspond to our practical prob-
lems.
Since H is a linear operator in a Hilbert space, it
can be written as:
H = ΨΘΨ
∗
,
where Θ : l
2
→ l
2
is characterized by the coefficients,
(θ
j,m,k,n
)
j,m,k,n
:= (hHψ
j,m
, ψ
k,n
i)
j,m,k,n
.
In order to justify the proposed approach, we first
recall some theoretical results presented in (Beylkin
et al., 1991) that assess the decrease of θ
j,m,k,n
away
from the diagonal (i.e. when |m −n|> 0 and |j −k|>
0). Then we provide an interpretation of the coeffi-
cients σ
j,n
in terms of amplitudes of the Fourier coef-
ficients of the local PSF.
3.1 Decay of Θ Away from the Diagonal
In (Beylkin et al., 1991), it has been proved that, for
compactly supported wavelets possessing M vanish-
ing moments and smoothly varying kernels, the val-
ues of Θ are small away from the diagonal in the one
and two-dimensional cases. Typical results are as fol-
low:
Theorem 1 ((Beylkin et al., 1991)). Suppose that
|K(x, y)|≤
1
|x−y|
and that K(x, y) is of class C
M+1
with
,
|∂
M
x
K(x, y) + ∂
M
y
K(x, y)| ≤
C
M
|x −y|
(1+M)
,
where M denotes the number of vanishing moments of
ψ. Then θ
j,m,k,n
satisfies the following inequality:
|θ
j,m,k,n
| ≤ O
1
1 + |j −k|
M+1
.
Moreover, for compactly supported kernels K:
|θ
j,m,k,n
| = 0,
for sufficiently large |m −n|.
The authors also show that the operator norm
kH −Ψ
˜
ΘΨ
∗
k can be made arbitrarily small if
˜
Θ is
obtained by thresholding Θ in such a way that only
O(n
d
) coefficients are kept. It roughly means that if K
is a smooth kernel, computing Hu can be performed
in O(n
d
) operations, rather than O(n
2d
), by making
use of the wavelet transform. In this work, rather than
considering sparse matrices
˜
Θ, we use simpler diago-
nal matrices.
We illustrate these results experimentally in the
discrete setting on Figure 3. We consider an operator
H whose kernel is a two-dimensional Gaussian with
variances linearly increasing in the vertical direction,
see Figure 2(c). This operator applied to the mandrill
image results in the image Figure 2(b). The matrix Θ
is shown on Figure 3. It is seen that Θ is dominated
by its diagonal entries and that the coefficients away
from the diagonal decrease extremely fast (actually
much faster than the result in Theorem 1).
3.2 Interpretation of the Diagonal
Values
In this paragraph, we show that the values σ
j,n
can
be interpreted as local frequency responses of
˜
H. We
assume that ψ is a compactly supported wavelet on
the interval [−β, β].
Let us analyze the impulse response of
˜
H at point
x:
˜
Hδ
x
= ΨΣΨ
∗
δ
x
=
∑
n∈Z
φ
l
0
,n
(x)φ
l
0
,n
+
∑
j≤l
0
,n∈Z
σ
j,n
ψ
j,n
(x)ψ
j,n
=
∑
n∈Z
φ
l
0
,n
(x)φ
l
0
,n
+
∑
j≤l
0
,
n∈k(x, j)
σ
j,n
ψ
j,n
(x)ψ
j,n
,
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
224
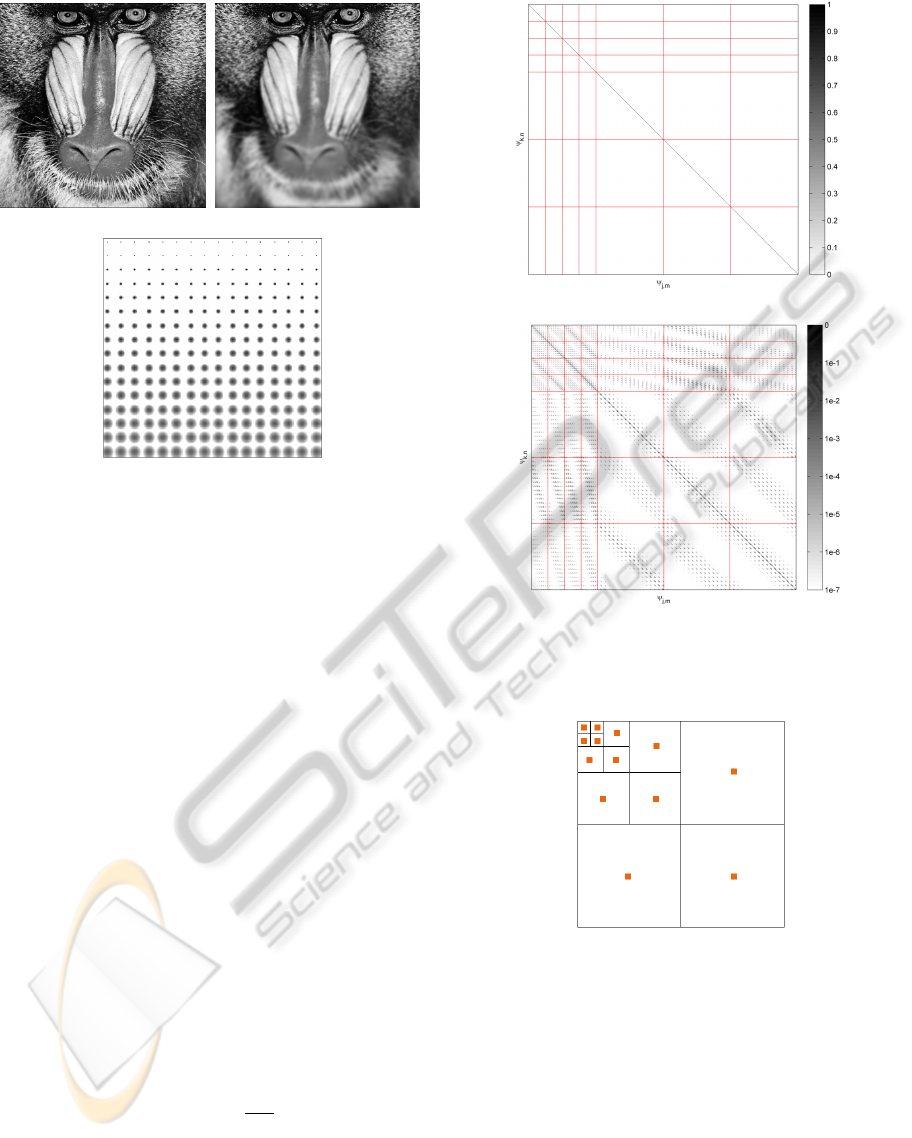
(a) Original Image (b) Blurred Image
(c) PSF at various locations
Figure 2: Image blurred using the operator H. The kernel
K of the operator is a Gaussian which grows linearly in the
vertical direction.
where
k(x, j) :=
n ∈ Z such that
2
−j
x −n
< β
.
The sets k(x, j) are represented in Figure 4 in the two-
dimensional case. They contain at most b2βc ele-
ments.
Now, if we assume that σ
j,n
varies little in k(x, j)
and satisfies σ
j,n
' σ
j,x
we obtain:
ΨΣΨ
T
δ
x
'
∑
n∈k(x,l
0
)
φ
l
0
,n
(x)φ
l
0
,n
+
∑
j≤l
0
σ
j,x
∑
n∈k(x, j)
ψ
j,n
(x)ψ
j,n
!
.
The local frequency response of
˜
H is thus
\
ΨΣΨ
∗
δ
x
'
∑
n∈Z
φ
l
0
,n
(x)
d
φ
l
0
,n
+
∑
j≤l
0
σ
j,x
∑
n∈k(x, j)
ψ
j,n
(x)
d
ψ
j,n
!
=
∑
n∈Z
φ
l
0
,n
(x)
d
φ
l
0
,n
+
∑
j≤l
0
σ
j,x
α
j,x
c
ψ
j
,
where α
j,x
is a complex coefficient that depends on
the choice of ψ and ψ
j
(x) =
√
2
−j
ψ(2
−j
x). Since
c
ψ
j
is well localized in the frequency domain, the coeffi-
cient σ
j,x
α
j,x
can be interpreted as a local frequency
attenuation in a certain frequency band that depends
solely on the scale j. This principle is illustrated in
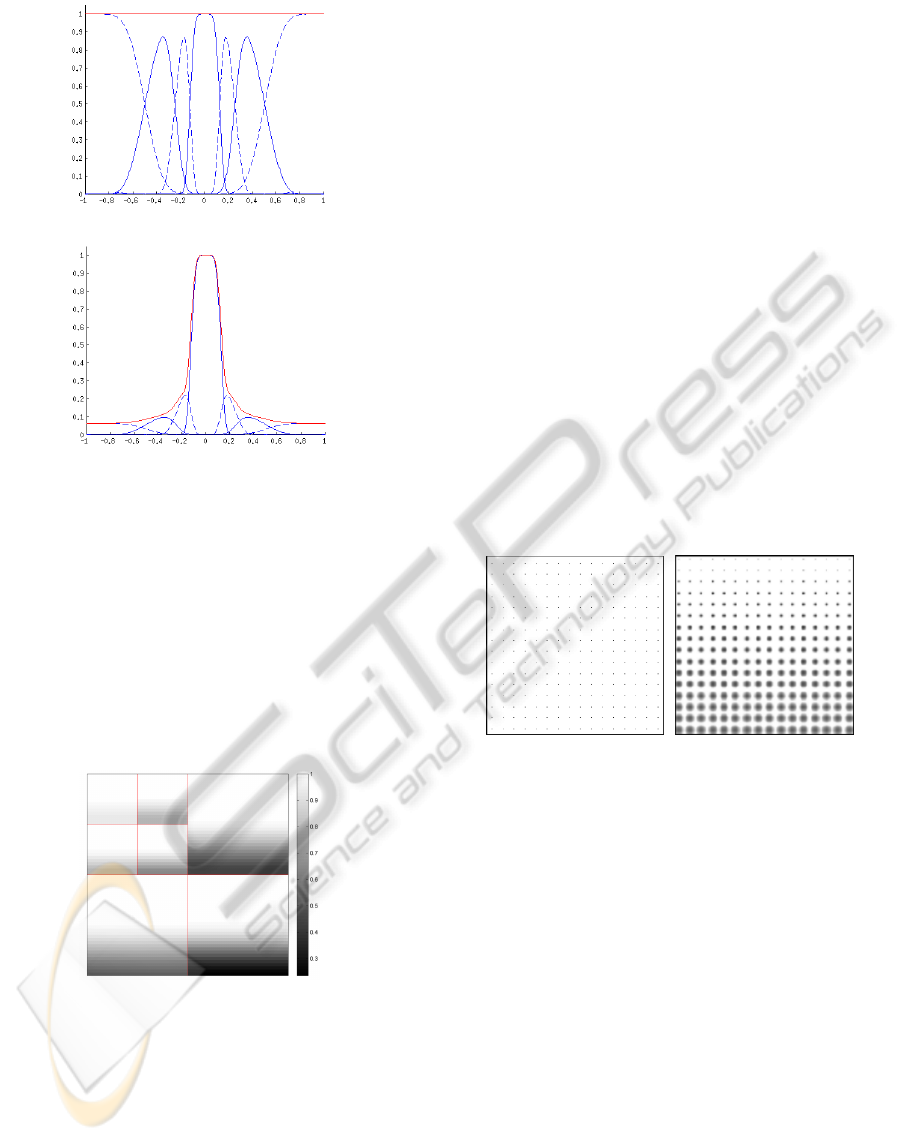
Figure 5.
(a) In a linear scale
(b) In a log
10
scale
Figure 3: Matrix Θ for the operator illustrated in Figure 2.
This matrix is obtained using Daubechies 8 wavelets and a
decomposition level J = 2.
Figure 4: The sets k(x, j) are indicated in orange at each
scale.
3.3 Spatial Regularity of the
Eigenvalues
A simple way to find a matrix Σ such that
˜
H ' H
consists in setting Σ = Diag(Θ). If the kernel K
varies sufficiently smoothly in space, the discrete val-
ues (σ
j,n
)
n∈Z
also vary smoothly, meaning that σ
j,n
'
σ
j,n+1
. This can be verified experimentally: Fig-
ure 6 represents the diagonal of Θ for an operator
H displayed in Figure 2(c) in the usual wavelet do-
SpatiallyVaryingBlurRecovery-DiagonalApproximationsintheWaveletDomain
225
(a) In blue
c
ψ
j
2
and in red
∑
j
c
ψ
j
2
(b) In blue |σ
j,x
α
j,x
c
ψ
j
| and in red
|
∑
j
σ
j,x
α
j,x
c
ψ
j
|
Figure 5: Local Fourier attenuation are determined by the
coefficients σ
j,x
α
j,x
.
main. The eigenvalues vary smoothly in each sub-
band. This remark is central to understand the inter-
polation algorithm proposed in the next section.
Also notice that the coefficients σ
j,n
decrease
from the top to the bottom of the image at each scale.
It means that the high-frequencies are attenuated on
the image bottom. This clearly corresponds to the op-
erator H shown in Figure 2(c).
Figure 6: Diagonal of the matrix Θ.
4 OPERATOR
RECONSTRUCTION FROM
LOCALLY KNOWN PSF
In this section, we propose a method to recover the
matrix Σ from the knowledge of local impulse re-
sponses. This setting corresponds to various practical
applications. In astronomy, stars may sometimes be
considered as Diracs. Their observation thus provides
the impulse response of the system K(x, ·), where x
denotes the star location. In microscopy, micro-beads
may be inserted in the sample and provide the impulse
responses at locations spread in the whole image do-
main.
The problem tackled in this section is the recon-
struction of K everywhere, from the knowledge of
K(x
i
, ·) at a few locations (x
i
)
i∈{1,···,m}
. We assume
that two images are available:
• An image
u =
m
∑
i=1
δ
x
i
,
that describes the Dirac locations.
• An image u
o
= Hu which provides the impulse
responses at locations x
i
.
Figure 7 illustrates two images u and u
o
. The Diracs
could be randomly located on the image rather than on
a uniform grid. We considered this simple setting for
experimental reasons. The number of known impulse
responses can also be considerably reduced as will be
shown later.
(a) The dirac map u (b) u
o
= Hu
Figure 7: Dirac map and the associated impulse responses.
This information is used to reconstruct an approximation of
the blurring operator H.
The knowledge of u
o
allows to reconstruct the
eigenvalues σ
j,n
of
˜
H only close to the known loca-
tions x
i
in each sub-band. These eigenvalues should
thus be interpolated in order to recover K everywhere.
Note that this problem is not standard since is consists
in interpolating an operator eigenvalues and not an
image.
Since the eigenvalues vary smoothly in space, we
propose to use bi-harmonic splines which are well
adapted to scattered data interpolation (Wahba, 1990).
The approximation problem we propose formulates as
the following variational problem:
Find Σ ∈argminkΨΣΨ
∗
u −u
o
k
2
2
+ λR(Σ), (3)
where λ > 0 is a regularization parameter. We also
set:
R(Σ) =
∑
j≤l
0
k∆σ
j
k
2
2
,
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
226

where ∆ denotes the discrete Laplacian and σ
j
de-
notes the set of eigenvalues at scale j. This energy
provides the approximation of minimal curvature. It
is equivalent to using bi-harmonic splines (Wahba,
1990).
The quadratic structure of problem (3) allows the
use of conjugate gradient like methods for the min-
imization. We are currently investigating the use of
preconditionners in the wavelet domain for accelerat-
ing the convergence.
We present approximation results in Figures 8 and
9. Figure 9 displays a interpolated matrix Σ. This
result can be evaluated by comparing it with the true
diagonal of Θ presented in Figure 6. Overall, the re-
construction leads to near perfect results. Figure 8
compares the interpolation provided by Fourier based
methods such as (Nagy and O’Leary, 1998) with the
proposed approach. Our method produces some ar-
tifacts, however, the proposed interpolation is rather
close to the reality in the image center. Note that this
result is obtained using knowing the PSF at only 4 lo-
cations in the plane. Deblurring an image with kernel
8(b) would be disastrous, since horizontal and verti-
cal frequencies would be enhanced, leading to strong
ringing artifacts.
(a) Exact PSF (b) Linearly Interpolated
PSF
(c) Our Interpolated PSF
Figure 8: Operator reconstruction using different methods.
The operator is reconstructed using the information avail-
able in the red rectangles.
5 RESULTS
In this section, we assume that the diagonal Σ has
been reconstructed using the method proposed in sec-
tion 4. We propose a total variation (TV) based algo-
rithm to tackle the deblurring problem. We suppose
that a degraded image v
o
is obtained according to the
following model v
o
= Hv+η where H : R
n
d
→R
n
d
is
the spatially varying blur operator, v ∈ R
n
d
is the un-
altered image and η ∈ R
n
d
is a white Gaussian noise,
Figure 9: The matrix Σ reconstructed using bi-harmonic
splines. It should be compared to the real diagonal pre-
sented on Figure 6.
η ∼ N (0, σ
η
Id
n
d
). Our aim is to recover v knowing
v
0
. Since
˜
H and H are usually compact, the problem
of recovering v is ill-posed and should be regularized.
We propose to use a standard total variation based re-
construction approach. It reads:
Find argmin
v∈R
n
d
,k
˜
Hv−v
o
k
2
2
≤α
TV (v), (4)
where α > 0 is a user fixed parameter and TV (v) is the
isotropic total variation of v defined in the notation. In
settings where H is perfectly known, users should set
α = σ
2
n. The proposed approach differs since total
variation serves as a regularizer for both the noise and
the errors in the operator approximation. In practice
we found that setting α = (1 + ε)σ
2
n where ε > 0 is a
small parameter provides good experimental results.
Problem (4) is solved using the primal-dual algorithm
proposed in (Chambolle and Pock, 2011).
In order to assess the method, we used the Man-
drill and Lena images rescaled in [0, 1] and blurred
with an operator having a two-dimensional Gaussian
PSF. In Figures 11 and 12 we respectively added a
noise of variance σ
η
= 0 and σ
η
= 3.10
−2
. In the case
σ
η
= 0, Figure 11 shows that the algorithm is able to
recover thin details of the image even in the coat and
the beard of the Mandrill. This highlights the fact that
the approximation of H by
˜
H is sufficiently good for
the sake of deblurring. In the case of a larger noise,
σ
η
= 3.10
−2
, Figure 12 shows that the image qual-
ity is improved but suffers from the standard defects
of total-variation based regularization: stair-case ap-
pears and thin details are not recovered. Images of
larger size can be found on the website of the authors.
ACKNOWLEDGEMENTS
This work was partially funded by the Mission pour
SpatiallyVaryingBlurRecovery-DiagonalApproximationsintheWaveletDomain
227
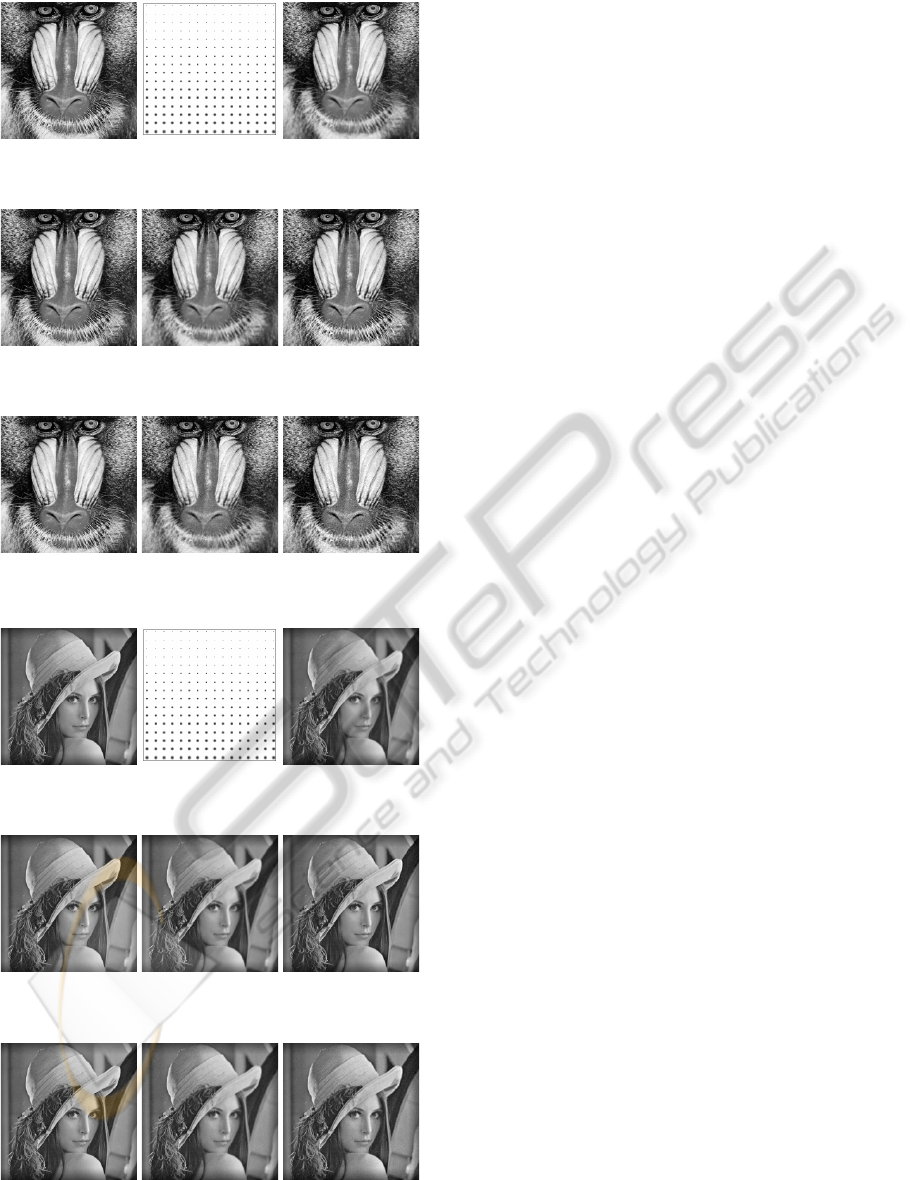
Figure 10: Original image, impulse responses and blurred
image.
Figure 11: Restoration results for σ
η
= 0. Degraded Image
SNR = 22.51dB, restored image SNR = 29.02dB.
Figure 12: Restoration results for σ
η
= 3.10
−2
. Degraded
Image SNR = 20.58dB, deblurred Image SNR = 20.86dB.
Figure 13: Original Image, impulse responses, blurred im-
age.
Figure 14: Restoration for σ
η
= 0. Original, degraded
SNR = 30.30dB, deblurred SNR = 36.13dB).
Figure 15: Restoration for σ
η
= 10
−2
. Original, degraded
SNR = 28.14, deblurred SNR = 29.18.
l’interdisciplinarit
´
e from CNRS, R
´
egion Midi
Pyr
´
en
´
ees and the ANR SPHIM3D.
The authors wish to thank J. Bigot and J. Fehren-
bach for interesting discussions. They also thank all
the ITAV staff, Charlotte Emery and Emmanuel Sou-
bies for their tireless support during this project.
REFERENCES
Beylkin, G., Coifman, R., and Rokhlin, V. (1991). Fast
wavelet transform and numerical algorithm. Commun.
Pure and Applied Math., 44:141–183.
Chambolle, A. and Pock, T. (2011). A first-order primal-
dual algorithm for convex problems with applications
to imaging. Journal of Mathematical Imaging and Vi-
sion, 40(1):120–145.
Chang, E.-C., Mallat, S., and Yap, C. (1999). Wavelet
foveation. Applied and Computational Harmonic
Analysis, 9:312–335.
Coifman, R. and Meyer, Y. (1997). Wavelets, calder
´
on-
zygmund and multilinear operators. Cambridge Stud-
ies in Advanced Math, 48.
Hansen, P., Nagy, J., and O’leary, D. (2006). Deblurring
images: matrices, spectra, and filtering. Siam.
Kirshner, H., Sage, D., and Unser, M. (2011). 3D PSF
models for fluorescence microscopy in ImageJ. In
Proceedings of the Twelfth International Conference
on Methods and Applications of Fluorescence Spec-
troscopy, Imaging and Probes (MAF’11), page 154,
Strasbourg, France.
Nagy, J. and O’Leary, D. (1998). Restoring images de-
graded by spatially variant blur. SIAM Journal on Sci-
entific Computing, 19:1063.
Preibisch, S., Saalfeld, S., Schindelin, J., and Tomancak, P.
(2010). Software for bead-based registration of selec-
tive plane illumination microscopy data. Nature meth-
ods, 7(6):418–419.
Temerinac-Ott, M., Ronneberger, O., Ochs, P., Driever, W.,
Brox, T., and Burkhardt, H. (2011). Multiview de-
blurring for 3-d images from light sheet based fluores-
cence microscopy. Image Processing, IEEE Transac-
tions on, (99):1–1.
Wahba, G. (1990). Spline models for observational data,
volume 59. Society for Industrial Mathematics.
Zhang, B., Zerubia, J., and Olivo-Marin, J. (2007).
Gaussian approximations of fluorescence microscope
point-spread function models. Applied Optics,
46(10):1819–1829.
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
228
