An in-Field Calibrating Method for the Bilateral Filter Applied to

X-ray Flat Panel Grayscale Images with High Spectral Resolution

Fabiana Oliveira Paixão Fernandes

, Cássio Alves Carneiro

, Petr Iakovlevitch Ekel

Zélia Myriam Assis Peixoto

and Flávia Magalhães Freitas Ferreira

Graduate Program in Electrical Engineering, Pontifical Catholic University of Minas Gerais,

500 Dom José Gaspar Avenue, Belo Horizonte, Brazil

University Center of Sete Lagoas, Sete Lagoas, Brazil

Keywords: Bilateral Filter, Image Denoising, X-ray Images, Flat Panel.

Abstract: Several spatial filters applied to images are available in technical and scientific literature. Besides the

reduction of the noise level, some of them also aim at the preservation of edges and details. Those filters are

commonly applied to the processing of X-ray medical image sequences, which are usually noised due to the

low doses of radiation suitable for medical procedures but where the loss of any detail may impair a

diagnosis. In this context, the bilateral filter is well suited. However, an adequate calibration of the bilateral

filter is required for reaching the best cost benefit between reducing the noise level and preserving the image

edges. Calibration procedures are still underexplored in the literature thereby, this paper proposes a new

method that allows in-field calibration of the bilateral filter embedded into a piece of equipment for

angiography, which uses a flat panel X-ray detector. The proposed method can be applied to images with

any spectral resolution and surpasses the performance of the calibration method presented in the literature.

1 INTRODUCTION

The acquisition of X-ray images is carried out under

strict conditions of exposure time of the patient to

radiation and X-ray dosage. However, decreasing

the dose implies increasing the image noise level

suppressing important details and thus hindering the

diagnosis. Therefore, denoising of medical X-ray

images is of great importance as there is also the

concern to preserve the characteristics of the image

(Zhang et al., 2009).

In those cases, temporal filtering techniques are a

good tool for preserving image details, beyond of its

low complexity of implementation. However, in

sequences of images where some movement is

present, e.g. digital angiography for hemodynamic

tests, the classic temporal filtering techniques cannot

be applied, because they cause trails in the motion

direction. Thus, spatial filters may be used instead.

These filters are accomplished with convolution

masks applied to the pixels of the image. As a result

they reduce the noise level but also cause edge

smoothing usually. This shortcoming precludes their

use for medical purposes since losses are not

commonly allowed in accurate diagnosis. However,

some spatial filters are more likely to preserve

edges. A suitable example is the bilateral filter,

which combines a domain filter to a range filter. The

first takes into account the spatial distance between

neighboring pixels to calculate the mask weights,

while the second is concerned about the difference

between their gray intensities (Tomasi and

Manduchi, 1998).

In (Gabiger-Rose et al., 2011) a procedure to

calculate the parameters of the bilateral filter for

grayscale images with spectral resolution of 8 bits

was proposed. However, there are few works in the

literature that carry out studies on the application of

the bilateral filter to medical images with high

spectral resolution, e.g., 14 bits.

In this paper, major concerns of the authors are

to guarantee an industrial in-field calibration method

for bilateral filter embedded into medical apparatus

of angiography that are built with an X-ray flat panel

detector. Nowadays the denoising process applied in

this kind of equipment to process sequences of

moving images is the same as 50 years ago, i.e.,

consisting of same classical spatial filters, such as

the averaging filter. Firstly our study proposes a

slight modification into the equations for the filter`s

163

Oliveira Paixão Fernandes F., Alves Carneiro C., Iakovlevitch Ekel P., Assis Peixoto Z. and Magalhães Freitas Ferreira F..

An in-Field Calibrating Method for the Bilateral Filter Applied to X-ray Flat Panel Grayscale Images with High Spectral Resolution.

DOI: 10.5220/0004315201630168

In Proceedings of the 3rd International Conference on Pervasive Embedded Computing and Communication Systems (PECCS-2013), pages 163-168

ISBN: 978-989-8565-43-3

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

parameters presented in Gabiger-Rose et al., (2011)

in order to extend the adjusting method of the

parameters to images with any bit resolution.

However, the largest contribution is the change in

that calibration methodology itself which results in

major gains in quality metrics when comparing to

the method of Gabiger-Rose et al., (2011).

This paper is organized as follows. After a brief

introduction of the bilateral filter in Section 2, a

short overview of the calibration method described

in Gabiger-Rose et al., (2011) is given in Section 3.

The proposed contributions that allow the in-field

calibrating method can be seen in Section 4. Section

5 shows experimental results already obtained and in

Section 6 one can find the conclusion of this work.

2 BILATERAL FILTER

The bilateral filter was firstly proposed by Tomasi

and Manduchi (1998) consisting of a discrete filter

applied in the spatial domain by using a convolution

mask, according to the Equation (1),

(,)( )

()

(,)

Wknxk n

Wkn











(1)

where W(k,n) weighs the contribution of each

neighboring pixel x(k-n) inside the mask regarding

the calculation of the value of the processed pixel

x(k), k is the location of the central pixel of the mask

and n is the distance between the central pixel and

its neighbor. The two-dimensional filtering can be

performed in two one-dimensional steps.

In the bilateral filter, the contribution W(k,n) of

each neighboring pixel corresponds to the product of

the weight W

(n) of a domain filter that depends on

the spatial distance between the two pixels and on

the weight W

(k,n) of a range filter that depends on

the difference between the intensities of both

(Giraldo et al., 2009). The weights W

(n) and

(k,n) are determined by Equations (2) e (3), in

which σ

and σ

are adjusting parameters of the

decay curve of the filters weights in function of the

spatial distance n and of the difference of intensities

x(k-n) and x(k), respectively. The idea is that even

neighboring pixels very close, but very different in

intensity, provide a small contribution in the result

of the spatial filtering. Thus, the image edges are

better preserved and the noise level is reduced

mainly in the regions in which intensity levels are

more uniform.

() exp











(2)



() ( )

(,) exp

xk xk n

Wkn













(3)

The calibration of the bilateral filter consists of

determining the parameters





and 



. It is

necessary to reach the best-cost benefit between

reducing the noise level and preserving the image

edges, objectives that are conflicting in nature.

3 ADJUSTMENT

3.1 Domain Filter

In Gabiger-Rose et al., (2011) it was presented a

method for the adjustment of the parameter σ

which depends only on the size of the convolution

mask. In order to approximate an ideal low-pass

filtering, the authors claim that the weighting

coefficients that would be outside the mask have to

be smaller than or equal to 10

-3

. This condition is

expressed in Equation (4), in which the size of the

one-dimensional mask is 2N+1.



max ( ) 10







(4)

For a convolution mask of dimension 7x1, which

proved to be in our experiments the most appropriate

for filtering purposes, the calculated value for the

parameter σ

obeying Equation 4, with N=3 and n=4,

was 1.08.

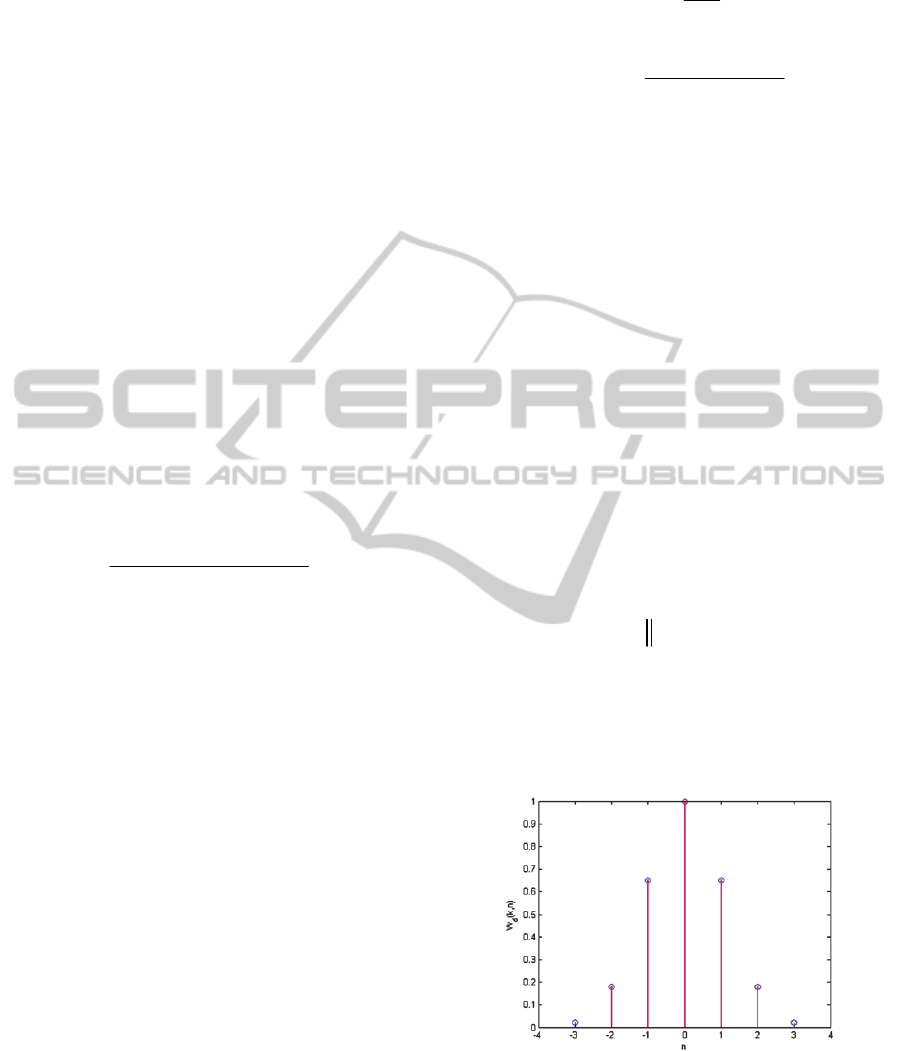
Figure 1: Weights of masks 5x1 and 7x1 using σ

=1.08.

However, if 



is equal to 1.08 in the 7x1 mask,

the value of the last coefficient inside the mask

(n=3) is very close to zero. Our first criticism of the

method refers to the mask 7x1 behaving very

similarly to the mask 5x1 as it can be observed in

PECCS2013-InternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems

164

Figure 1, which depicts the weights W

(n), for n

varying from –N to +N, for masks 7x1 (blue circles)

and 5x1 (red bars).

3.2 Range Filter

The parameter σ

must be adjusted based on the level

of noise present in the image in order to reach the

best-cost benefit between reducing the noise level

and preserving the image edges.

Thus, in Gabiger-Rose et al., (2011) it was

proposed the determination of the parameter 



as

the product of the noise standard deviation and a

factor R (Equation 5) which must be determined in

order to maximize either of the quantitative

performance metrics. The suggested metrics are the

PSNR (Peak Signal to Noise Ratio) and the MSSIM

(Mean Measure Structural Similarity) (Wang et al.,

2004), as a means of gaining perceptual proximity

with the Human Visual System (HVS). While PSNR

is measured in dB, MSSIM varies between 0 and 1

and evaluates quantitatively how close the output

image is of a reference image, in terms of intensity,

structure and contrast. Best results reflect on values

of MSSIM near 1.

r noise





(5)

To check the dependence of R in relation to the

statistical characteristics of noise, Gabiger-Rose et

al., (2011) used a test database composed by 50

images of 8-bit whose pixels were not normalized,

where it was included an additive Gaussian noise of

zero mean and variable standard deviation



noise

(variation in the range of 1 to 64, in steps of 4).

Images were filtered using a bilateral filter with

fixed 



(calculated using Equation 4) and with 



calculated according to Equation (5), trying values

of R in the range of 0.5 to 16, in steps of 0.5. The

metrics PSNR and MSSIM are calculated separately

for each image, and finally, the average of these

metrics, considering all the images for each pair

(



noise

, R) is determined. These mean values then

become the characteristic values of the metrics for

each specific pair (



noise

, R). The idea is to choose

the parameter R that maximizes both characteristic

metrics, for each value of the parameter 

noise

In order to highlight the differences among the

characteristic metrics obtained by using different

values of R, the characteristic metrics which refer to

a specific



noise

are normalized in relation to the

maximum value of that same set, in accordance with

Equation 6. Thus, the highest value of the

characteristic metrics for a specific



noise

is mapped

to the value 0 and its null value is mapped to the

value 1. If we generate a grayscale image aiming at

easier viewing and interpretation of these values, the

dark line at this image corresponds to the best

performance for different



noise

. Figure 2 shows the

visualization of data relating to the normalized

characteristic PSNR.

0.2

metrics

metrics 1

metrics

average

norm

max









(6)

Figure 2: Normalized characteristic PSNR as a function of

R and 

noise

(Gabiger-Rose et al., 2011).

4 SENSITIVITY ANALYSIS OF

THE BILATERAL FILTER AND

THE IN-FIELD CALIBRATION

Unlike Gabiger-Rose et al., (2011), that found the

most presumably suitable parameter



according to

Equation 4 and kept this value invariant while

seeking the optimal R for different



noise

, our method

consists in applying a sensitivity analysis of the filter

regarding the parameters



and R, in order to

improve the adjustment of these parameters aiming

at optimizing either of the metrics, at a specific level



noise

Furthermore, the calibration method presented in

Gabiger-Rose et al. (2011) was applied only to 8 bits

grayscale images. However, medical images are

generally encoded with 14 bits. Thereby, in order to

make the calibration procedure independent of

spectral resolution, we first normalize the image

pixels between 0 and 1.

In the calibration procedure, an industrial

phantom acquired in real conditions of medical

procedures must be used due to the need for having

sequential multiple still images in order to find a

reference image, presumably noise-free, for the

calculation of the metrics. This procedure is not

possible with real medical images since it would

submit the patient to long exposures to X-rays. The

calibration phantom must have density

Anin-FieldCalibratingMethodfortheBilateralFilterAppliedtoX-rayFlatPanelGrayscaleImageswithHighSpectral

Resolution

165

characteristics that simulate different tissues of the

human body as well as frequency components that

simulate structures present in the medical procedures

such as blood vessels, bone structures, calcifications

and catheters. The phantom image is processed by

bilateral filter and the filtered image is compared to

the reference image in order to compute the metrics.

The reference image is obtained from a temporal

average of 8 frames of the calibration phantom,

acquired at different times. The value of



noise

necessary to compute



in accordance with

Equation 5

is estimated from the histogram of the

difference between one of the noisy image frames

and the reference image after normalizing their

pixels.

In our experiments, the calibration phantom

image shown in Figure 3 was acquired with the

equipment AngiX III FD, manufactured by Brazilian

company Xpro. The estimated value for



noise

was

0.026. The sensitivity analysis with respect to the

filter parameters was performed by varying both σ

and R. The first varied from 0.5 to 5, in steps of 0.5

and the second varied from 0.5 to 10, in steps of 0.5.

The metrics PSNR and MSSIM were calculated for

the calibrating phantom image for each (



, R) pair.

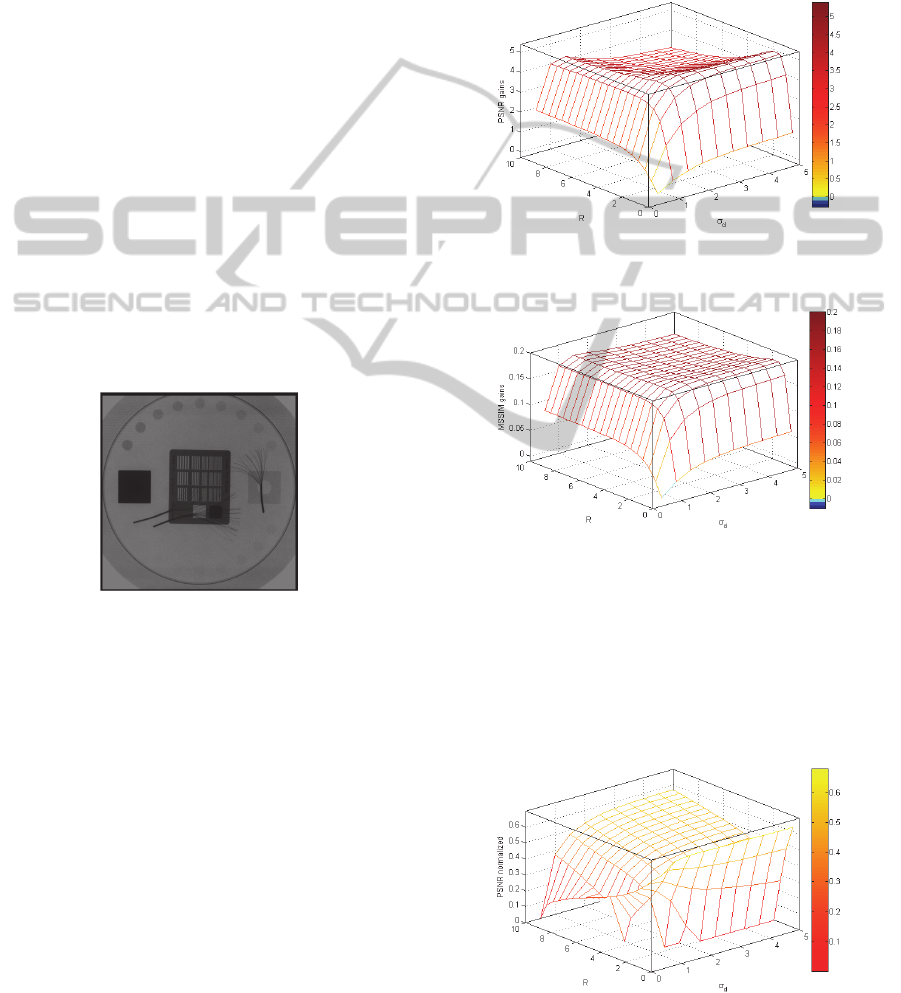
Figure 3: Calibrating phantom image.

Figures 4 and 5 provide visualization of PSNR

and MSSIM gains for helping with the analysis of

filter sensitivity to the parameters adjustment in

which the hot colors correspond to positive gains

while the cold colors correspond to negative gains,

respectively. The metrics gain refers to the

difference between the metrics for the filtered image

and the metrics for the noisy image, before the

application of the filter. The graphs in Figures 6 and

7, in turn, correspond to the metrics (PSNR and

MSSIM, respectively) normalized in accordance

with Equation (6), where metrics

max

corresponds to

the maximum value of each metrics for a fixed value

of 



. These figures do not intend to compare the

performance of the filter to each (



, R) pair.

Instead, they just give an insight into the

determination of the optimum R for a specific value

of 



,since they assign, with a zero value in the z-

axis, the value of R that optimizes the filter

performance at each 



From Figures 4 and 5, it can be noticed that the

best performance of the bilateral filter is achieved

for larger values of 

, which contradicts the choice

of the parameter 

proposed in Gabiger-Rose et al.

(2011).

Figure 4: PSNR gains (dB) as a function of



and R using

the calibrating phantom.

Figure 5: MSSIM gains as a function of



and R using the

calibrating phantom.

From Figures 6 and 7, it can be verified that the

lower the value of



, the larger the expected value

of R aiming at optimizing performance. However,

for values of



greater 2.5, the optimum R does not

change and it is equal to 2 for the calibration

phantom.

Figure 6: Normalized values for PSNR (dB) as a function

of σ

and R using the calibrating phantom.

PECCS2013-InternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems

166

It is worth noticing that the classic average filter

is equivalent to the bilateral filter with the highest

values of



and R. In other words, it corresponds to

the worst performance of the bilateral filter.

It is concluded from the proposed calibration

method and using the shown calibration phantom,

we choose to adjust the two parameters of the

bilateral filter with values 



3 and R=2, using a

7x1 convolution mask.

Figure 7: Normalized values for MSSIM as a function of

and R using the calibrating phantom.

5 RESULTS

The in-field calibrated bilateral filter (implemented

in Matlab) was then used to reduce the noise level at

the image of a test phantom, shown in Figure 8, also

acquired by AngiX III FD in equivalent conditions

of real medical procedures. The achieved gains of

PSNR and MSSIM are shown in Table 1 at three

different conditions: first, 



1.08 and R=5 which

are the values found through the method presented

in Gabiger-Rose et al., (2011); second, 



3 and

R=2 which are the optimum values found by our

calibrating method; and third, 



3 and R=10

which corresponds to the classic average filter for

which the PSNR presented a decrease of 0.231dB.

Table 1: PSNR and MSSIM gains using the test phantom.





PSNR gains

MSSIM gains

Gabiger-Rose et al. (2011)

1.08 5 2.7093 0.0948

Our in-field calibratin method

3 2 3.0753 0.1085

Classic average filter

3 10 -0.231 -0.0327

Making a subjective analysis on images of

Figure 8, it is noticed that with 



3 and R=10 the

image is plainly blurry, that is, visible losses occur at

the edges. With the method presented in Gabiger-

Rose et al., (2011), 



1.08 and R=5, the noise

level is not reduced as expected.

The bilateral filter was also applied on a real

medical image with 14 bits, shown in Figure 9.

Although the metrics PSNR and MSSIM cannot be

calculated due to the lack of the reference image, we

compared the performance of our in-field calibration

procedure to the performance of the method

presented in Gabiger-Rose et al., (2011) by

analyzing the visual quality of the filtered images.

Visual inspection of the image obtained from the

classic average filter is also performed. It can be

noted that the perceptual analysis carried out for the

real medical image leads to the same achievements

gotten for the test phantom.

6 CONCLUSIONS

The bilateral filter is used in several recent papers

and it is notable for owning the feature of preserving

edges. However, the literature lacks a clear and

efficient procedure to calibrate the parameters of this

filter. The majority of papers that process grayscale

images encoded with 8 bits only mentions the values

of the used parameters of the filters and do not show

the way they were determined. Fortunately, from the

calibration procedure presented in Gabiger-Rose et

al., (2011) for 8 bits images, we were able to

generalize the original proposal to the case of

images with any spectral resolution. Besides that, we

present a more accurate industrial in-field procedure

to find the values of the parameters of the filter that

optimize either PSNR or MSSIM using a phantom

image acquired by the X-ray flat panel equipment

itself. The denoising process of X-ray images using

the bilateral filter properly calibrated gave us a

superior result in terms of noise level reduction and

edge preservation, when comparing to works

presented in recent literature. This was verified not

only from metrics calculated from phantom images

but also from visual inspection of filtered real

medical images. It is important to stress that our

proposal is that this industrial in-field calibration

procedure can be applied in practical operation

conditions of medical pieces of equipment of

angiography that use X -ray flat panel detector. The

method intends to provide X-ray images with higher

quality independent of flat panel manufacturer, as

well as of total harmonic distortion of the network

power distribution and of other parameters that

influence the quality of the acquired images, like

local temperature and humidity.

Anin-FieldCalibratingMethodfortheBilateralFilterAppliedtoX-rayFlatPanelGrayscaleImageswithHighSpectral

Resolution

167

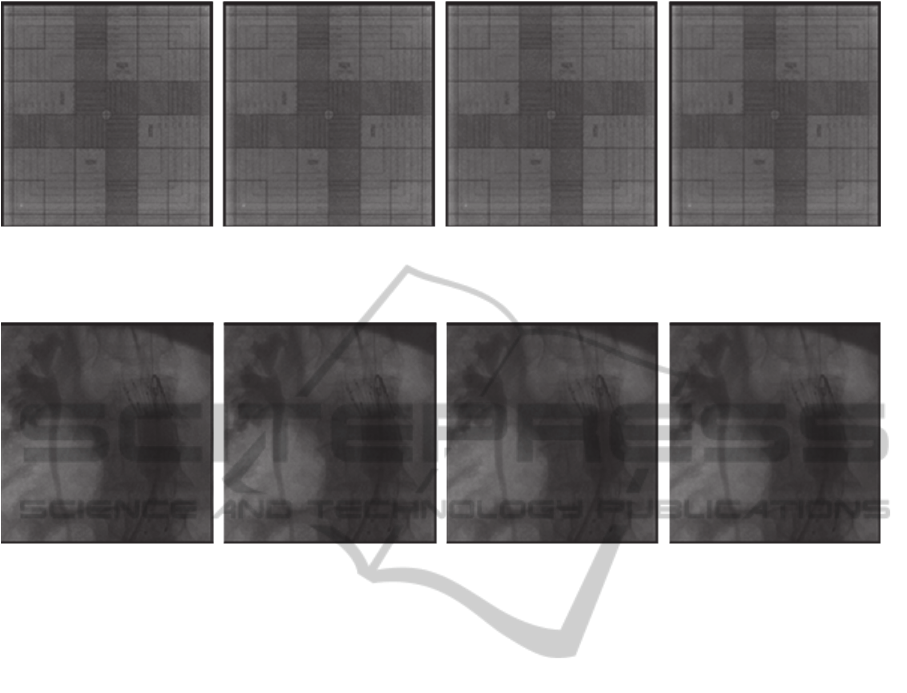
(a) (b) (c) (d)

Figure 8: Test phantom (a) noisy image (b) denoised image: 



1 and R=5 (c) denoised image: 



3 and R=2 (d)

denoised image: 



3 and R=10.

(a) (b) (c) (d)

Figure 9: Medical Image (a) noisy image (b) denoised image: σ

=1 and R=5 (c) denoised image: σ

=3 and R=2 (d) denoised

image: σ

=3 and R=10.

REFERENCES

Gabiger-Rose, A., Kube, M., Schmitt, P., Weigel, R., &

Rose, R., (2011). Image Denoising Using Bilateral

Filter With Noise-Adaptive Parameter Tuning. 37th

Annual Conference on IEEE Industrial Electronics

Society.

Giraldo, J., Kelm, Z., Guimaraes, L., Yu, L., Fletcher, J.,

Erickson, B. and McCollough, C., (2009).

Comparative Study of Two Image Space Noise

Reduction Methods for Computed Tomography:

Bilateral Filter and Nonlocal Means. 31st Annual

International Conference of the IEEE EMBS.

Minneapolis, Minnesota, USA.

Tomasi, C., and Manduchi, R., (1998). Bilateral Filtering

for Gray and Color Images. IEEE International

Conference on Computer Vision. Bombay, India.

Wang, Z., Bovik, A., Sheikh, H. and Simoncelli, E.,

(2004). Image Quality Assessment: From Error

Visibility to Structural Similarity. IEEE Transactions

on Image Processing, 13, 600-612.

Zhang, L., Chen, J., Zhu, Y. and Luo, Z., (2009).

Comparisons of Several New De-Noising Methods for

Medical Images. 3rd International Conference on

Bioinformatics and Biomedical Engineering.

PECCS2013-InternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems

168