
Towards a Sustainable Smart e-Marketplace
A Stable, Efficient and Responsive Smart Exchange with Strategic Conduct
Wafa Ghonaim
1
, Hamada Ghenniwa
1
and Weming Shen
2
1
Electrical and Computer Engineering Dept., Western University, 1150 Richmond Street, London, Ontario, Canada
2
Integrated Manufacturing Technologies Institute, National Research Council, London, Ontario, Canada
Keywords: Smart Exchange, Double Auction, GSP Auction, Reverse GSP Auction, GSP Matching, Bidding Language,
Strategic Rules, Bidding Lifecycle, Preference Elicitation, Preference Formulation, Winner Determination.
Abstract: The landscapes of e-marketplaces are changing profoundly, evident in the phenomenal growth and potential
of online services, consumers, and enabling mobile technologies. However, it is unleashing grave concerns
about sustainability due to the fierce competitions, fuzzy dynamics and rapidly shifting powers. While it is
attributed to the game-theoretic economics and computation complexities of the decentralized combinatorial
allocation problem, this work establishes, denying e-traders expressing fair strategic choice is unfounded of
adverse strategic risk. In fact, free market dynamics realize impact of smart learning on strategic conduct.
The fact strategic rules enable faster consumer-to-market bidding lifecycle is another compelling factor.
Hence, the work introduces the novel rule-based bidding language and GSPM double auction for the smart
exchange that facilitates expressions of strategic rules, while uniquely exploits forward and reverse GSP
auctions for efficient, tractable, stable, and budget balanced e-marketplace. The e-marketplace deliberates
on rules for effective preference elicitation, while bringing self-prosperity in socially efficient ecosystem.
1 INTRODUCTION
Emerging e-marketplaces as in online advertising
are undergoing seismic changes, quite evident in the
phenomenal growth and potential of online services,
engaged e-users, and enabling mobile technologies.
However, it is unleashing serious concerns about its
sustainability due to the fierce competitions, fuzzy
dynamics and rapidly shifting powers. In fact, the
striking impact of digital markets is stirring industry
to diligently fetch more viable service delivery and
revenue models that thrive in a e-market ecosystem
(Moore, 1996). Hence, the enduring power struggle
amongst rivals is polarizing towards fetching more
efficient and sustainable ecosystem friendly dynamic
mechanisms for trading of services and information
liquidity. While it is attributed to the game-theoretic
economics and computational complexities of the
decentralized combinatorial allocation problem
(CAP) of services amongst self-interest rational e-
traders (i.e. agents), who may strategize on private
preferences, this work establishes, denying e-traders
expressing fair strategic conduct is unsubstantiated
of adverse strategic risk. In fact, the emerging trend
of real-time bidding on user attentions increases the
complexity of economically inspired decentralized
CAPs. While this work investigates and realizes the
complexities of e-marketplaces, formally, it reveals
and examines, also, few strategic overlooked issues.
The first issue relates to the fact present e-
marketplaces restrain scope of strategic conduct thru
mechanisms that grant incentives for non-strategic
acts or, rather, penalize levies to be paid to losing
bidders due to strategizing. For instance, the VCG
(Vickrey, 1961) (Clarke, 1971) (Groves, 1973)
mechanisms, penalize for strategizing, by reporting
non truthful preferences to align payoffs with social
welfare, rather than the desirable self-prosperity.
Ironically, truthful mechanisms often benefit the
revenue maximizing intermediaries (marketplaces),
rather than their alleged computation efficiency. In
fact, trading restrictions, often, promote adverse
strategic natural reactions of rational smart agents
that may extend to incomplete or false information
revelation, given higher expected payoffs. Adverse
strategies may be manifested by fraud, deception,
collusion, shilling, free riding, shading, snipping or
hidden actions. In fact, e-marketplaces are more
vulnerable to adverse strategies than classic markets.
Software agents might collude by submitting
untruthful reduced bids for false partial requirements
or form coalitions that benefit from super-agent
338
Ghonaim W., Ghenniwa H. and Shen W..
Towards a Sustainable Smart e-Marketplace - A Stable, Efficient and Responsive Smart Exchange with Strategic Conduct.
DOI: 10.5220/0004316503380345
In Proceedings of the 5th International Conference on Agents and Artificial Intelligence (ICAART-2013), pages 338-345
ISBN: 978-989-8565-39-6
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

power. Traders may, also, unleash several agents
with multiple identities for false name bidding.
Hence, this work establishes, denying e-traders (e-
buyers and e-sellers) expressing strategic conduct,
allegedly, to improve computation efficiency as in
Google DoubleClick, Microsoft AdECN, Yahoo
Right Media, and Facebook FBX, is unsubstantiated
of dire business impact, given modern enabling hi-
tech is transforming computation into commodity.
Indeed, the flexible expressions of fair strategic
conduct that bring self-prosperity would, ultimately,
mitigate adverse strategies that may defy markets,
considering, often, higher risks and lower expected
returns (Fair vs. adverse strategies to be examined in
a coming work), given the dynamics of smart
learning thru social interactions and repetitive trades.
In fact, Adam Smith envisions traders interacting in
free markets act as if guided by “invisible hand” that
leads to desirable outcomes (i.e. efficiency and
stability) due to markets’ inherent flexibility of
natural free choice and smart interaction. In fact,
free market dynamics promote realizing impact of
continuous learning on strategic conduct. However,
free market efficiency would, often be realized with
market thickness, uncongested interaction, and safe
privacy (Roth, 2007). This work extends it, also, to
applying fair rules of game-theoretic encounter (i.e.
no enforced monopolistic rules). However, while
online services gold rush and thriving technologies
have tilted trader tactics to conceding to e-market
restrictions, apparently, at the expense of strategic
benefits, for the direct gains of easy access to the
wealth of inventories and information liquidity,
sustainability would be exposed, at which priorities
align with the natural expression of strategic conduct
higher returns, and better quality of service.
In the second issue, the work establishes the lack
of rapid consumer-to-marketplace automation during
bidding lifecycles is another compelling challenge to
expressing strategic conduct. In fact, the time wasted
in bidding processes at e-marketplaces like eBay,
Amazon, etc. is an irritating engagement experience.
For instance, a bidding lifecycle may take days, for
an e-Bay auction, with rather manual configurations.
Hence, the work introduces the concept of “bidding
lifecycle”, examine it effectiveness in divers trades
and establishes, the flexible expressions of strategic
rules (i.e. sub-programs) during the bidding process
that are collected, stored and exploited by the smart
exchange (SX), to deliver rapid bidding lifecycles.
The third challenge relates to the mounting
combinatorial complexity of online ad problem
evident in the emerging real-time bidding (RTB) of
single users’ attentions. RTB allows advertisers bid
for single impressions, using user profiles, cost
thresholds, and campaign goals to optimally assign
bid values at real-time. RTB provides more liquidity,
visibility, and competitive bidding, essential for the
sustainable growth. In fact, contemporary e-markets
are exploiting the complex multichannel engagement
user experiences of online services that facilitate
better market openness, and transparency. However,
the combinatorial complexity (i.e. cherry-picking) of
user level trades lack of efficient control, massive
growth, and fierce competition are main concerns
Finally, a common issue in the decentralized e-
markets relates to the implemented computation
mechanism design for SX-CAP. The game-theoretic
economics and computation complexities of the SX-
CAP are observed in the GSP auction (Varian, 2007)
(Edelman, Ostrovsky, & Schwartz, 2007), while it is
allocative efficient (AE), it is not incentive
compatible (IC) and often, maximizes auctioneer’s
revenue, rather than traders’. Conversely, while
VCG auction is efficient and stable it is, often,
intractable and runs at deficit. The iterative models
(Ausubel & Milgrom, 2006) (Parkes, 2006), take
longer time to converge with no guarantees of either
AE or stability, an issue tackled, for instance, by
iterative VCG (Parkes, 2001).The work, hence,
targets a SX model that delivers an efficient, stable
and tractable e-trading allocation for self-interested
rational traders with independent private information
and strategic conduct of rather conflicting goals.
This work examines and reflected on overlooked
issues and, ultimately, develops a novel “rule-based”
bidding language (RBBL) for smart exchange (SX)
that allows for flexible expressions of smart strategic
rules formulae. The RBBL is fully symmetric that
enables flexible and rapid e-trading while unlocking
the natural expressions of strategic conduct, not only
for e-buyers, but, also, for e-sellers, often, confined
with the reserved values. The RBBL empowers the
SX to deliberate smart rules for rapid preference
elicitations and valuations that ultimately, delivers
rapid bidding lifecycle. The inherent game-theoretic
economics and computation complexities of SX and
the emerging combinatorial complexity of e-trading
of user attentions, inspire designing the GSP based
double auction (DA) matching (GSPM) that
uniquely blends forward and reverse GSP auctions
to achieving self-prosperity (i.e. max utility), social
efficiency, strategic stability and computational
tractability. The GSPM exploits the recent business
successes and endorsements of the efficient, yet
simple GSP auction (Edelman, Ostrovsky, &
Schwartz, 2007) (Varian, 2007) and the theoretical
Nash stability of GSP repeated best response auction
(Nisan, Schapira, Valiant, & Aviv, 2011). The
RBBL and GSPM, ultimately, empower bidders and
SX with flexible expressions of smart rules and
interaction pattern, smart preferences elicitation and
efficient winner determination. The SX would,
eventually, provide a timely seamless access to the
TowardsaSustainableSmarte-Marketplace-AStable,EfficientandResponsiveSmartExchangewithStrategicConduct
339

ever growing inventory and information liquidly
with stability self-prosperity, and social efficiency,
while reducing friction and refining transparency.
Thus, sustainability is secured the win-win dynamics
of the naturally free e-market ecosystem. Section 2
presents a formal model of online ad problem and
pertaining issues. Section 3 introduces the rule based
bidding language, while the formal GSPM double
auction model is investigated in section 4. Section 5
concludes with a remark on the ongoing work.
2 ONLINE PROBLEM MODEL
2.1 The Online Problem Description
This work targets a class of multiple-unit, multiple-
attribute CAP of online services (i.e. impressions)
amongst self-interest rational e-trader agents with
conflicting goals that motivate strategic conduct,
expressed as smart rules for, indeed, maximizing
their expected utilities, given their belief about other
trader preferences. The GSPM DA for SX-CAP
assumes, however, truthful states of choices for a
sound mixed integer program (MIP) and winners’
determination (WD) matching problem. For online
ad problem, the commodity of the e-marketplace is
ad impression, (i.e. a single viewing of single ad by
a single user). The SX allows symmetric bidding of
both e-buyers and e-sellers with rather expressions
of smart rules on factor-groups (FG). FG may, for
instance, be an age group, location, interest, etc.
Hence, an ad impression is designated by specific
factors (i.e. webpage, user profile, service content,
etc.) within a time period. Considering time is a set
of discrete decision periods during which multiple e-
services are allocated to multiple winners, the work
assumes allocation and pricing decisions are taken
off-line at the end of any decision periodτ. The SX-
CAP manifests sequence of events, as fairly tabled
in (Mansour, Muthukrishnan, & Nisan, 2012) for ad
exchange. Followed is a formal description of the
online ad problem in the ad SX during period:
1. Upon online users browsing of publishers
(e-sellers) webpages,∀
∈
…
…
,
forms
impressions,
…
…
of user, publisher and webpage profiles.
,
…
,
…
,
, ad
asset has
distinct FG attributes∀
∈
.
2.
, bids
⋃
,
,
,“asks” on impression
assets
.
,
,
, is sets of
ask-bids,
∋
is impressions set,
∋
is
associated ask-prices set and
∋
is smart
rules set.An ask-bid price is sum of factor-
group values of
impression asset in
: Let
…
…
ask values of
; then
ask-bid price is
∑
.
The pricing model may exploit cost per-factor
(cpf), per-group (cpg) or per-impression (cpi).
3. The SX announces impressions contextual info
and quality scores
⋃
.
,
, to advertisers
…
…
∀
,
,
,,
is SX quality scores (QS) on webpage publisher
and user at τ as derived by SX intelligence and
deliberation. The SX stores bidding rules
of
publishers while hiding prices
to mitigate
strategic impact of exposure problem.,
…
…
is publishers’ impression assets,
while
…
…
is SX QS set.
4. Advertisers,
∈, collect
,
,
info
and returns request-bids that target either user
attentions or segment
⋃
,
,
,
,
,
for
asset.
, is allocated budget.
,
,
is request bid with
, bid values and
, the
associated rules of
…
…
∋
=
,
…
,
…
,
;
∈
=
…
…
.
…
…
, is
the pricing set of
∈
.∀
, let
…
…
set of best bid-price values
on
FGs, the total offered-price on
is
∑
,
bid for, given
≥
if matched else no bid returned. RBBL is
used for bid choices, valuations and smart rules.
5. The SX applies GSPM double auction (DA)
matching allocations and payments for winners
using forward and reverse GSP auctions, fter
collecting all request and ask bids. The SX
computes efficient allocations and payments. It
returns
,
∗
,
,
∗
to wining
, ∀
and
,
∗
,
∗
to wining
,∀
.
∗
,
∗
, are SX pricings for matched
,
pair on
, while
∗
, is media asset to
be dispatched and
is
budget.
6. Publisher
serves webpage
with winning
ad
∗
atτ for ad impression
.
, allocates
the dispatched
∗
to a specific location that
fulfils the impression- request as matched with
impression-asset.
Example: An advertiser wish to bid ad impressions
at Segment level
:
:,
:
: or at user level
∪
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
340
: Loc,
:California), (
:Ag,
:Gen X)}, or
∪ {(
:Day part,
:Morning),
(
:Content,
: Super Bowl)},etc. of possible
factor-group values
…
…
and total
∑
. Figure 1, depicts the
online ad problem model in smart exchange.
Publisher (e-Seller) 1
Local Problem: LP
P
1
Impression Assets: I
P
1
QS: QS
P
1
Utility: u
P
1
(
x
)
Publisher (e-Seller) j
Local Problem: LP
P
j
Impression Assets: I
P
j
QS: QS
P
j
Utility: u
P
j
(
x
)
Advertiser (e-buyer) 1
Local Problem: LP
A
1
Requests: I
A
1
QS: QS
A
1
Utility: u
A
1
(
x
)
Publisher (e-Seller) m
Local Problem: LP
P`
m
Impression Assets: I
P
m
QS: QS
P
m
Utility: u
P
m
(
x
)
Advertiser (e-Buyer) i
Local Problem: LP
A
i
Requests: I
A
i
QS: QS
A
i
Utility: u
A
i
(
x
)
Advertiser (e-Buyer) n
Local Problem: LP
A
n
Requests: I
A
n
QS: QS
A
n
Utility: u
A
n
(
x
)
Publisher
Agent-P
j
Advertiser
Agent-A
1
Smart Exchange e-Marketplace: SX
Global Problem: SX-CAP
Social Objective: f(U
P
(S),U
A
(S))
Allocation Rule:
x
Payment Rule: π
x
QS: QS
x
j
Ask
Bid
Bid
Bid Ask
Ask
Online User 1
Profile: U
1
QS: QS
u
1
Online User m
Profile: U
m
User QS: QS
u
m
Online User j
Profile: U
j
QS: QS
u
j
B
r
o
w
s
e
Browse
Browse
Advertiser
Agent-A
i
Advertiser
Agent-A
n
Publisher
Agent-P
1
Publisher
Agent-P
m
• • •
• • •
• • •
• • •
Rule-Based Bidding Language (RBBL) with Smart Rules
Rule-Based Bidding Language (RBBL) with Smart Rules
Stored Smart Rules
Smart Preference Elicitation
GSPM DA Matching
Smart Rules Delibration
Preference Elicitation Queries
Smart Rules Analysis
Figure 1: The Online ad problem Model in Smart
Exchange.
2.2 The SXCAP AE Matching Problem
The SX computes an efficient-trade rather than
optimal- revenue-trade, as there are many competing
e-traders and networks, so it is unfeasible to exercise
monopoly power. The work assumes e-trader agents
act exclusively as either service providers or service
consumers. The SX computes an efficient outcome
allocations and payments from agents’ reported
valuations, or smart rules preference elicitation that
usually, involve solving an NP-hard CAP. In fact,
the WDP in CAs (and thus also in CEs) is NP-hard
(Rothkopf, Pekec, & Harsrad, 1998). Generally, the
objective of the SX is to implement a trade
∗
for the
SX-CAP at period that delivers social efficiency.
The SX selects then payment rule that drives IC,
individual rationality (IR) (i.e. agent expected payoff
payoff of non‐participating), with budget balance
(BB) (i.e. total cross SX payments =0, or non‐
negative). Formally, assume
∅
0 with free
disposal (i.e. agents have weakly increasing values
for services
∀
⊃
. Let e-
trade
,
=
1, points to impressions
and
are matched (i.e.
=
for same FG
attributes, and the request-bid on
and ask-bid on
are eligible for trade;
,
0,
otherwise. ∀ e-trader agents of quasi-linear utilities
,
∀
∈
∀clearing price,
∈.
, is negative, if
bidder receives a payment for the trade. Bidders are
modeled as being risk neutral (i.e. agent pays as
much as the expected value of an item) with budget
constraints (i.e.
) for ad campaign (e.g. frequency
of playback of ad
. The SX-CAP is limited by
constraints (bids and budgets), rules, objectives, and
mechanism. Given instance
,,
at period,
the efficient
∗
is, then, given as follows:
Definition 1: Given instance
,,
of true bids
at,
1 if
,
0 otherwise,
then efficient trade
∗
solves:
.
∀,1
;
∀
,∀
∈
,0
..
1,∀
,∀
2
1,∀
,
3
.
∀
,
4
.
05
|
|
,|
|
6
,
∈
0,1
∀
,
7
Constraint (C7) ensures integrality, while (C2, C3)
restrict a request-bid on specific unique impression
to be assigned at most to one ask bid of the same
unique ad impression, and restrict an ask-bid on an
offered unique impression to be assigned at most
one request- bid of the same. The SX-CAP, hence,
turns into the generalized assignment problem
known to be NP-Hard; (C4, C5) ensure budget
balance (BB), and restricts budget boundaries
(i.e.
), while (C6) impose strict balance in items’
supply-demand by free disposal. The above SXCAP
problem is an instance (i.e. reduction) of set-packing
problem (SPP) (deVries & Vohra, 2003). In fact, the
SPP is a functional reduction of the SXCAP
transformed in polynomial time (i.e. SPP
SXCAP). The SPP is NP-Hard, but the recognition
version is NP-complete (deVries & Vohra, 2003).
Thus, the SXCAP is NP-complete and can’t be
solved using exact approaches (i.e. branch and
bound, Cutting planes etc.). Due to the decentralized
TowardsaSustainableSmarte-Marketplace-AStable,EfficientandResponsiveSmartExchangewithStrategicConduct
341

nature of the problem, however, this work adopts an
economic based approach for SX-CAP modeling.
3 THE RBBL SMART BIDDING
3.1 Expressing Strategic Conduct
Economists often advocate free markets as the right
way to organize economic activities, in which
economic social welfare is not a priority, but rather
self-prosperity. However, free markets have proven
successful in organizing economic activities for the
social well-being (Mankiw, 2012), despite their
inherent flexibility that enables traders to exploiting
strategic conduct. However, present e-marketplaces
restrain scope of strategic conducts, due to alleged
computation limitations. This work argues, denying
users expressing their natural strategic conduct,
while limiting preference space would have a dire
impact on business sustainability. In fact, the tight
restrictions on strategic behaviour and e-trading
practices, often, promote adverse strategic reactions
that disrupt social efficiency. Hence, this work
envisions a sustainable SX e-marketplace empowers
consumers with strategic conduct on e-trading and
interaction patterns using a flexibly expressive
bidding language (BL). The SX should deliberate on
smart rules for effective preference elicitation, while
computing efficient allocations and payments. The
SX, should, eventually, provide a seamless access to
the ever increasing online services, inventories and
information liquidly, for the benefit of consumers
and e-marketplaces, the result of win-win dynamics
in naturally free markets ecosystem.
3.2 Bidding Lifecycle Analysis
An inspiring drive to developing the RBBL is to
improving consumer-to-marketplace performance by
extending the bidding “lifecycle” and exploiting
distributed computing. The bidding lifecycle relates
to the period bid can be active throughout diverse
trades before it get expired and dropped off the
trading platform. The work realizes the performance
impact of frequent biddings that might require
frequent manual setups (i.e. eBay, Amazon, etc.).
While irrelevant in classic markets, it has a major
impact on digital e-markets, considering the huge
number of online transactions. Hence, minimizing
bidding lifecycle would have a crucial impact on
designing effective SXs another compelling for
applying smart rules. For instance, iterative bidding
of indirect mechanisms (i.e. English auction), has
short multiple round bidding lifecycles to each trade
and requires extra time for bid formulation. Hence,
clock auction mitigates impact by enforcing time
constraint for rapid response. The proxy iterative
bidding shortens the bidding lifecycle using proxy
agents (see (Parkes, 2006)) with valuation bounds
and provisional allocation that works until market
clears, for single e-trades. On the other extreme
there are the bidding programs (Nisan, 2000), in
which the complete formal problem model is sent to
and solved by the e-marketplace. However, bidding
programs are not feasible due to core computation,
valuation and privacy problems. Direct mechanisms
(i.e. GSP auction) use complex bidding, with short
lifecycle that ends each e-trade with the execution of
WD. This work develops, hence, the RBBL for
distributed multiple trades. The RBBL enables rapid
bidding lifecycle by using complex rules stored in
the SX for smart preference elicitation on multiple e-
trades that enables rapid performance. The RBBL
enables, also, distributed computation between e-
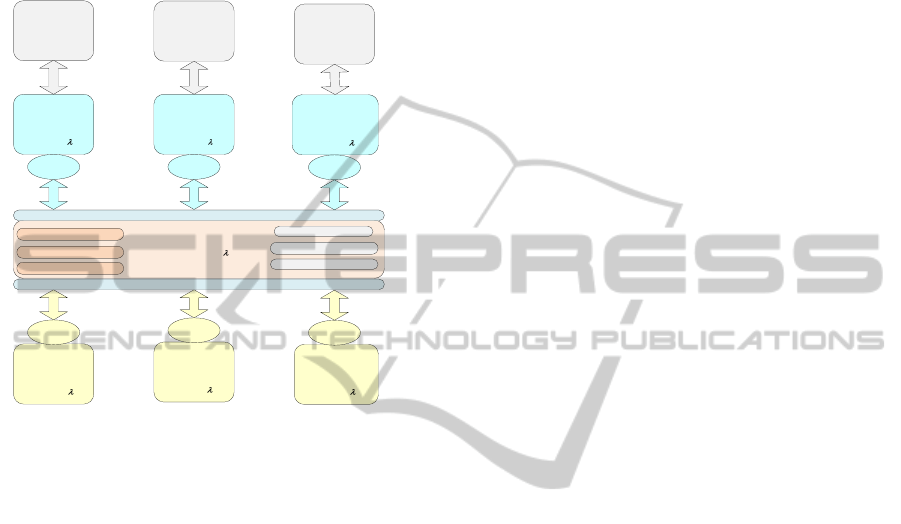
trader software agents and SX engine (see Figure 2).
Figure 2: Rule Based Bidding (Distributed for Multiple
Trades).
3.3 The Rule Based Bidding Language
This work presents the SX computation model to
managing online trading using an expressive bidding
structure that empower consumers with complex
rational interaction patterns, and flexible level of
strategic freedom. In that vein, the work introduces
the RBBL that generalizes and blends the TBBL in
(Cavallo, et al., 2005), logical
and
(Boutilier
& Hoos, 2001), that include
,
,
, OR‐of‐
XORs, XOR‐of‐ORs, and
∗
with Nisan’s bidding
programs (Nisan, 2000), and various preference
elicitation models in (Sandholm & Boutilier, 2006),
while facilitating expressions of strategic conduct
with flexibility, expressiveness, consciences for a
computationally tractable, efficient and stable. The
RBBL is symmetric that allows e-traders to bidding
buys and sells in single tree structure that exploits
“complex rule” operators (
) for smart preference
elicitation, formulation, and efficient WD.
An instant of the RBBL bid tree structure is
shown Figure 3. The gray blocks refers to the
‘s
that may be expressed using propositional logic
(PL), first order logic (FOL), temporal logic (TL),
etc. (not shown in this work) that reflects the
dynamic constraints applied to a given situation. The
may represents campaign duration, if “Ask bids
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
342

Figure 3: RBBL bid structure.
active time
”); tactics, “At lost trade, increase
value of factor by for next trade, stop at upper
bounds
”; “When number of win trades 2,
reduce value by, stop at lower limit
”; “CNN
ad impressions? Increase value by for next trade,
stop at upper bound
”; logic operators “”,
“If, then, else” rule;
TBBL, AND, OR, XOR,
OR*, etc.
′ , reduce the complexity of dynamic
choices. The SX stores
′ for smart deliberation
and effective preference elicitation, rather than
solving complete bidding programs. The SX
descripts
′, then, rather than full enumeration; it
deliberates
′ to elicit preferences and
valuations. In fact, the diverse types of
′, add
smart filters to reducing combinatorial complexity
by narrowing down the feasible solution space. Bids
are expressed as annotated bid trees of either e-sell
or e-buy nodes. RBBL has
′ on internal nodes
for propagating values within the tree. Leaves of the
tree are annotated with traded items and nodes are
annotated with changes in values. RBBL facilitates
direct (one-shot) and indirect (iterative) mechanisms
and is captured as MIP, while facilitating effective
rules deliberation and smart preference elicitation
for efficient winner determination.
3.4 The RBBL Properties
Followed are propositions on the RBBL that briefly
define related game-theoretic and computational
properties. Analyses, formal proofs and verification
of which, though, are found in another work:
Proposition 1: RBBL generalizes pervious bidding
languages (i.e.
,
and
,
,
, OR‐
of‐XORs, XOR‐of‐ORs, and
∗
, TBBL, extended
TBBL) and extends to complex rules, constrains and
valuations for direct and indirect mechanismsis.
Proposition 2: RBBL facilitates direct (one-shot) and
indirect (iterative price-taking) mechanisms.
Proposition 3: RBBL captured as MIP, facilitates
effective preference formation and elicitation for
efficient winner determination. The SX stores and
descripts complex rules of all bids, then, rather than
full enumeration; it applies smart learning heuristics
to elicit dynamically preferences and valuations.
Proposition 4: RBBL is scalable, allows for sub-bids
that can be analyzed by multiple processors. RBBL
prevent the exposure problem by hiding budgets,
using XOR like substitutable bids.
4 THE GSPM DOUBLE AUCTION
Double auctions are, often, used in exchange
markets, such as stock exchange (i.e. NYSE),
commodity markets (i.e. CME), etc. While the work
targets desirable IC, AE, etc. for the DA design of
SX, it is, often hard for a DA to have them all. In
(McAfee, 1992) and (Wurman, Walsh, & Wellman,
1998) , for instance, there is no DA that is both AE
and IC. This work , however, introduces a unique
GSP based DA the exploits the fact while GSP is not
IC, GSP repeated best response strategies converge
to Nash equilibrium with VCG AE IC outcomes and
payments, as analyzed and validated in (Edelman &
Ostrovsky, 2007) (Varian, 2007) and (Nisan,
Schapira, Valiant, & Aviv, 2011). Hence, the GSP
based DA for SX achieves desired properties with
repeated best repose strategies. While at IC, traders
maximize their utilities with truthful revelation of
private choices, AE assures maximizing aggregate
valuations of buyers and sellers. Other desired
proprieties are BB (i.e. total surplus generated equal
available surplus at NE), SX profit maximization
(i.e. max sum of differences between request and ask
bid prices of all matched pairs) and IR, where the net
benefit to each e-trader from using the DA is less
than the net benefit of any alternative.
4.1 The GPM Double Auction Model
The DA equilibrium matching (EM) (Wurman,
Walsh, & Wellman, 1998) is a common sealed-bid
matching that is IC, in which clearing price does not
depend on matching bid prices, but externalities. EM
finds uniform equilibrium prices
∗
that balances
request and ask bids so all eligible requests with
price
∗
and asks with
∗
are matched
using 4‐Heap algorithm that implements the IC last
matched
auction for single‐unit sellers and first
unmatched 1
auction for single‐unit buyers.
TowardsaSustainableSmarte-Marketplace-AStable,EfficientandResponsiveSmartExchangewithStrategicConduct
343

However, EM IC is not applicable to multi‐unit bids
or symmetric buys and sells. In fact, EM DA can be
IC or AE but not both (McAfee, 1992). To maximize
matches, it is essential to allow price discrimination
in which different matches cleared at different
prices. IC is hard to achieve, also, in dynamic DA
(e.g. stock exchange), where bids are entering or
leaving over time and there is more than one
matching to search sequentially (Parkes, 2007). The
work in (Zhao, Zhang, & Perrusse, 2010), presented
maximal matching (MM) DA that maximizes market
liquidity, allocations, and profit, yet, is not IC.
As stated earlier, to tackle the combinatorial
complexity of RTB, this work introduces the GSPM
DA, GSP discriminatory pricing model. As shown
Figure 4, GSPM exploits the GSP forward auction
for e-buyers, while proposes a reverse-GSP auction
for e-sellers. At time, given requests
∈
and
ask bids
∈
, the GSPM algorithm: (1) Qualifies
eligibility by identifying and grouping eligible pair
matches (i.e.
w.r.t. factor-groups, (2)
Sorts eligible ask (request) bids in ascending order
of forward GSP (descending of reverse GSP) auction
w.r.t. bid values; (3) Process Matching, start at the
top, add ask‐request pairs to the matching list, if ask-
bid pricerequest-bid price as per definition 2; (4)
Computes Allocations, based on results, assign
matched pair
,
to advertiser
and publisher
; and (5) Assigns prices, following definition 3.
4.2 The GSPM Properties
The development of GSPM model is inspired by the
analysis of (Edelman, Ostrovsky, & Schwartz, 2007)
for envy-free Nash equilibrium, (NE) that is
equivalent to the “Symmetric NE” (Varian, 2007) as
well as the findings in (Nisan, Schapira, Valiant, &
Zohar, 2011), in which, while truth telling is not
dominant strategy under GSP, the full information
repeated best response strategy (BRS) GSP has NE
with VCG AE IC outcomes. Followed are brief
definitions and theorems that briefly define the
GSPM game-theoretic economics and computation
properties. However, the analyses, formal proofs and
verification of which are detailed in another work:
Definition 2: [GSPM DA Matching and Allocation
Rules]: Let ∪the set of traders, and ∩ ∅,
for exclusive trade, as per problem assumption. Let
∪
set of request and ask bids. Let ask-bid
,
=
∈
and request bid
,
=
∈
. Sort eligible ask
(request
) bids in
ascending order of forward GSP (descending of
reverse GSP) auction w.r.t. bid values. Then, the
ordered set of matched ask-request pairs
,
…
,
…
,
is a GSPM DA
matching set, if ∀matched ordered pair
,
,
prices
, ∀
,
, .
Then, is a GSPM list of eligible ordered pairs.
Definition 3 [GSPM DA Pricing Rule]: the ask-price
for≤ matched pair is
,
,
the ask price of 2
nd
matched pair
,
. The
request-bidder price for matched pair
is
,
, the request-price of 2
nd
matched pair
,
. For last match ,
traders pay their request and ask bid values,
,
;
,
).
Figure 4: GSPM double auction model for ad impressions.
Proposition 5 [GPSM DA AE]: The GSPM DA
mechanism that implements AE social choice (SC)
function, maximizes total payoffs by maximizing
total valuations of e-buyers, while minimizing total
cost of e-sellers given IR e-trader agents, hence,
maximizing the total profit the SX marketplace.
Theorem 1: The GSPM DA with BRS is AE
Theorem 2: The GSPM DA maximizes SX revenue.
Theorem 3: The GSPM with repeated BRS is IC.
Theorem 4: GSPM DA is ex post weak BB.
Theorem 5: GSPM DA is ex-post IR.
Definition 4 [locally envy-free NE]: Equilibrium
(“Symmetric NE” (Varian, 2007)) of the GSP
simultaneous-move game is locally envy-free if
bidder cannot improve payoff by switching bids
with the bidder ranked one position above her”
(Edelman, Ostrovsky, & Schwartz, 2007)
Theorem 5: GSPM has NE with repeated BRS.
5 CONCLUSIONS
This work presents formal analysis and modeling of
the GSPM, GSP based double auction and RBBL,
rule-based bidding language for smart exchange.
The work argues denying traders free expressions of
fair strategic conduct, challenges sustainability and
provokes adverse strategic reactions. This work
establishes, also, lack of consumer-to-marketplace
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
344

rapid bidding cycles is another compelling factor to
realizing the strategic choice. The work examines
the bidding lifecycle model and establishes strategic
bidding delivers more efficiency, better automation
and fairly distributed computing. Hence, the RBBL
enables the flexible expressions of strategic conduct
using smart rules. The smart exchange exploits the
smart rules to deliberating on effective preference
elicitation. The GSPM tackles inherent and evolving
combinatorial complexities by uniquely exploiting
both forward and reverse GSP auctions, for a
truthful, efficient, stable and tractable matching that
delivers rapid automation, self-prosperity, and social
efficiency with a seamless access to the massively
growing inventories and information liquidly. The
smart exchange e-marketplace secures, ultimately,
the business sustainability, by reducing friction and
improving transparency, in the win-win dynamics of
the naturally free e-markets ecosystem. The work is
ongoing, however, on game-theoretic economics and
computation efficiency of the GSPM and RBBL
with focus on sound empirical validation and results.
REFERENCES
Ausubel, L., & Milgrom, P. (2006). Ascending Proxy
Auctions. In P. Cramton, Y. Shoham, & R. Steinberg,
Combinatorial Auctions (pp. 79-98). MIT Press.
Boutilier, C., & Hoos, H. (2001). Bidding languages for
combinatorial auctions. Proceedings of the 17th
International Joint Conference on Artificial
Intelligence, (pp. 1211–1217).
Cavallo, R., Parkes, D. C., Juda, A. I., Kirsch, A., Kulesza,
A., Lahaie, S., et al. (2005). TBBL: A Tree-Based
Bidding Language for Iterative Combinatorial
Exchanges. Multidisciplinary Workshop on Advances
in Preference Handling (IJCAI).
Clarke, E. H. (1971). Multipart pricing of public goods.
Public Choice, 11, 17-33.
deVries, S., & Vohra, R. V. (2003). Combinatorial
auctions:A survey. Informs Journal on Computing,
15(3), 284–309.
Edelman, B., & Ostrovsky, M. (2007). Strategic bidder
behavior in sponsored search auctions. Decision
Support Systems, 43, pp. 192–198.
Edelman, B., Ostrovsky, M., & Schwartz, M. (2007,
March). Internet Advertising and the Generalized
Second Price Auction: Selling Billions of Dollars
Worth of Keywords. American Economic Review,
97(1), 242-259.
Groves, T. (1973). Incentives in teams . Econometrica ,
41, 617-631.
Mankiw, G. N. (2012). Principles of Microeconomics (6E
ed.). South-Western Cengage Learning.
Mansour, Y., Muthukrishnan, S., & Nisan, N. (2012).
Doubleclick Ad Exchange Auction (Submitted).
Computer Science and Game Theory.
McAfee, R. P. (1992). A Dominant Strategy Double
Auction. J. Economic Theory, 56, 434–450.
Moore, J. F. (1996). The Death of Competition:
Leadership and Strategy in the Age of Business
Ecosystems. New York: Harper Business.
Nisan, N. (2000). Bidding and Allocation in
Combinatorial Auctions. Proc. ACM Conf. Electronic
Commerce (pp. 1-12). ACM Press.
Nisan, N., Schapira, M., Valiant, G., & Aviv, Z. (2011).
Best-Response Auction. Proceedings of the 12th ACM
conference on Electronic commerce. ACM.
Nisan, N., Schapira, M., Valiant, G., & Zohar, A. (2011).
Best-Response Auctions. Proceedings of the 12th
ACM conference on Electronic commerce (EC '11).
ACM.
Parkes, D. C. (2001). An Iterative Generalized Vickery
Auction: Strategy Proofness without Complete
Revelation. Proceedings of AAAI Spring Symposium
on Game Theoretic and Decision Theoretic Agents,
(pp. 78-87).
Parkes, D. C. (2006). Iterative Combinatorial Auctions. In
P. Cramton, Y. Shoham, & R. Steinberg,
Combinatorial Auctions (pp. 41-77). MIT Press.
Parkes, D. C. (2007). Online Mechanisms. In N. Nisan, T.
Roughgarden, E. Tadros, & V. Vazirani (Eds.),
Algorithmic Game Theory (pp. 411-439). Cambridge
University Press.
Roth, A. E. (2007). The Art of Designing Markets.
Harvard Business Review , 85(10), 118–126.
Rothkopf, M. H., Pekec, A., & Harsrad, R. M. (1998).
Computationally manageable combinatorial auctions.
Management Science, 44(8), 1131-1147.
Sandholm, T., & Boutilier, C. (2006). Preference
elicitation in combinatorial auctions. In P. Cramton, Y.
Shoham, & R. Steinberg (Eds.), Combinatorial
Auctions. MIT Press.
Varian, H. R. (2007). Position Auctions. International
Journal of Industrial Organization, 25(7), 1163-1178.
Vickrey, W. (1961). Counterspeculation, auctions and
competitive sealed tenders. Finance , 19, 8-37.
Wurman, P., Walsh, W., & Wellman, M. (1998). Flexible
double auctions for electronic commerce: Theory and
implementation. Decision Support Systems, 24, 17−27.
Zhao, D., Zhang, D. K., & Perrusse, L. (2010). Maximal
Matching for Double Auction. Australasian
Conference on Artificial Intelligence, 516-525.
TowardsaSustainableSmarte-Marketplace-AStable,EfficientandResponsiveSmartExchangewithStrategicConduct
345
