Consistency of UML Class and Statechart Diagrams

with State Invariants

Ali Hanzala Khan, Irum Rauf and Ivan Porres

Department of Information Technologies,

Abo Akademi University,

Abo, Finland

Keywords:

Model Consistency, Class Diagram, Statechart Diagram, State Invariants, OCL, Reasoning, OWL 2.

Abstract:

We present an approach and a tool to analyze the consistency of UML class and statechart diagrams containing

state invariants automatically. UML class diagrams describe the structure of a system as a collection of classes

while UML statechart diagrams describe its behavior. State invariants relate the active state conﬁguration of

a statechart with object instances described in a class diagram. We consider a UML statechart inconsistent if

it contains unsatisﬁable state invariants, that is, there are no object instances that can make a given invariant

evaluate to true. To detect such inconsistencies, we translate a UML model containing class and statechart

diagrams into the Web Ontology Language (OWL 2), and then use OWL 2 reasoning tools to infer the con-

sistency and satisﬁability of the translated diagrams. The approach is supported by an automatic translation

tool and existing OWL 2 reasoners. We demonstrate our approach with an example design and evaluate its

performance using large UML models.

1 INTRODUCTION

The Uniﬁed Modeling Language (UML) is a widely

used modeling notation for documenting the design

of software intensive systems (OMG, 2011). A UML

model usually comprises a number of diagrams pro-

viding different views of a system. These diagrams al-

low us to decompose the design of a large system into

smaller and more manageable views. However, rep-

resenting a system as a collection of diagrams raises

the issue of possible design inconsistencies. In this

article we address the problem of the consistency of

UML class and statechart diagrams with state invari-

ants.

A class diagram describes the structure of a sys-

tem in the form of classes, their associations with each

other, the attributes of each class and operations that

can be invoked on them. On the other hand, a stat-

echart diagram provides the behavioral interface of a

class. It deﬁnes all possible sequences of method in-

vocations, the conditions under which methods can be

invoked and their expected results.

Each state in a statechart diagram represents a cer-

tain condition that is true when the state is active. The

condition can be implicit in the design, or deﬁned ex-

plicitly in the form of a state invariant. A state invari-

ant is a boolean expression that is true when a given

state is active and false otherwise. State invariants are

deﬁned using the attributes and associations described

in the class diagram and expressed using the Object

Constraint Language (OCL) (OMG, 2006).

Given a number of UML class and statechart dia-

grams, it is possible to specify unsatisﬁable state in-

variants that describe states that can never be active

or operations that cannot be implemented according

to the well-formedness rules speciﬁed in the UML su-

perstructure speciﬁcation (OMG, 2011). An unsatis-

ﬁable state invariant is considered inconsistent with

respect to a class diagram since there are no object in-

stances that can make an unsatisﬁable invariant eval-

uate to true.

The inconsistent state invariants are design errors

and, in order to reduce development costs and time,

they must be detected and corrected as early in the

software development process as possible. The ap-

proach we propose to detect such inconsistencies is

based on the use of the automatic reasoning tools de-

veloped initially in the context of the semantic web.

We ﬁrst translate the class and statechart diagrams

with state invariants in a UML model to the Web

Ontology Language version 2 for Description Logic

(OWL 2 DL) (W3C, 2009b), and then use an OWL 2

DL reasoning tool (Sirin et al., 2007; Shearer et al.,

2008; Tsarkov and Horrocks, 2006) to determine the

consistency of the UML design.

The approach presented here is limited to a frag-

Khan A., Rauf I. and Porres I..

Consistency of UML Class and Statechart Diagrams with State Invariants.

DOI: 10.5220/0004320100140024

In Proceedings of the 1st International Conference on Model-Driven Engineering and Software Development (MODELSWARD-2013), pages 14-24

ISBN: 978-989-8565-42-6

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

ment of the OCL language, but on the other hand

is decidable and fully automatic. The designer does

not need to know the details of the translation or the

reasoning performed by the underlying tools. Also,

current reasoning tools and desktop computers can

process relatively large UML models in few seconds.

Therefore we consider that this approach has the po-

tential to be integrated with existing and future UML

tools and provide consistency analysis services that

go beyond what is being offered in current tools that

only use basic syntactic analysis and well-formed

rules.

This paper is organized as follows. In Section 2,

we present an overview of our approach with the help

of a running example and discuss the related work. In

Section 3, we discuss the problem and the proposed

solution for determining the consistency of a UML

model containing class and statechart diagrams. In

Section 4, we present the structure and the transla-

tions of class diagrams, statechart diagrams and state

invariants into OWL 2 DL. In Section 5, we discuss

about the implementation of the UML to OWL 2

translations in the form of a translation tool and the

consistency analysis by using OWL 2 reasoners. Fi-

nally, in Section 6, we conclude the paper.

2 CONSISTENCY OF CLASS AND

STATECHART DIAGRAM

In this section we present an overview of our approach

that we demonstrate with a running example and dis-

cuss previous work related to the consistency of UML

diagrams.

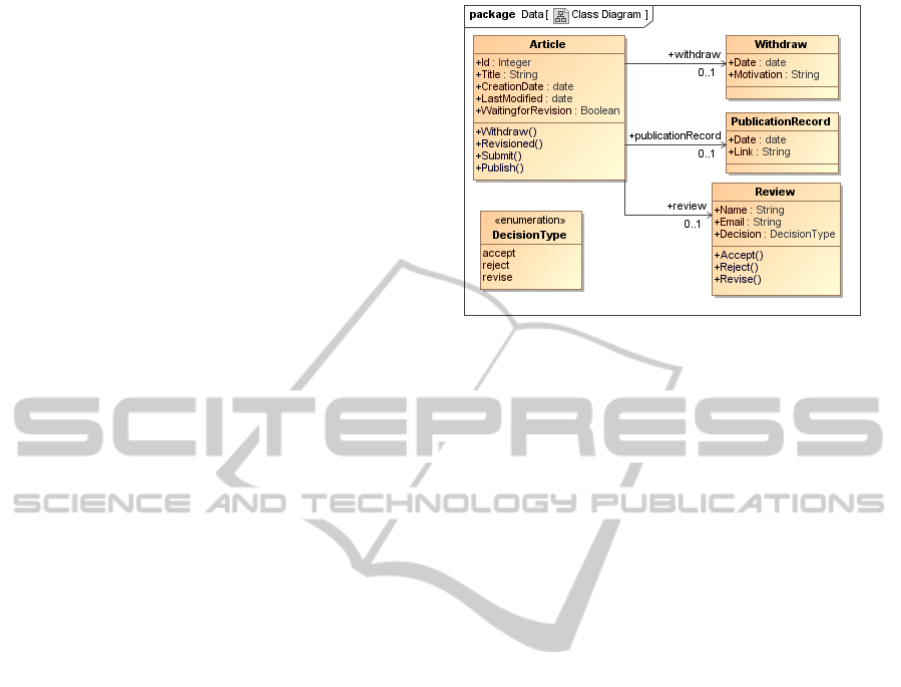
Our example system is a Content Management

System. In this system, authors post new articles to

be published after being reviewed by a reviewer. A

reviewer can accept, reject or advise a revision of the

paper. Only an accepted article can be published. An

article can be withdrawn if it is under review. How-

ever, a published article cannot be withdrawn. The

structure of this system is described as a UML class

diagram (Figure 1), while its behavior is described us-

ing a UML statechart diagram (Figure 2).

A statechart diagram deﬁnes behavior of a class in

terms of states that an instance of a class takes during

its lifecycle and the transitions between them. Each

transition from a source to a target state is triggered

by a function call.

The statechart diagram shown in Figure 2 deﬁnes

the behavioral view of the class Article of the class

diagram shown in Figure 1 in term of states. It con-

sists of one composite state ArticleReview and two

simple states Publish and ArticleWithdraw. The Ar-

Figure 1: The static view of Content Management System.

ticleReview composite state consists of four simple

states namely, WaitingforReview, Revisioning, Arti-

cleRejected and Accept. When the submit() method is

called on an object of the class Article, the statechart

diagram is initiated and the object enters into the state

WaitingforReview a substate of ArticleReview. The

method calls to accept(), reject() and revise() take the

object to the Accept, ArticleRejected and Revisioning

state respectively. When the author of the article is

revisioning the article, the object of the class Article

is in the Revisioning state. When the author revises

the article, he invokes the Revisioned() method of the

Article class and the object again comes into the Wait-

ingforReview state. The publish() method can be in-

voked from the Accept state and the object switched to

the Publish state. An article can be withdrawn by in-

voking the method withdraw() whenever the state Ar-

ticleReview is active, but the withdraw() method can-

not be invoked if the object of the class Article is in

the Publish state.

Each state in a statechart is annotated with a state

invariant. The state invariant is a boolean expression

that links classes of a class diagram to the states of a

statechart diagram. We say that an object of a class

is in a certain state if the state invariant of that state

is true. We express the state invariant of each state

by using OCL and annotate the behavioral diagram

of our example with state invariants in Figure 2. The

details about the OCL constructs used in our approach

will be discussed in Section 4.4.

We consider the state invariants which let the stat-

echart diagram behave against the UML superstruc-

ture speciﬁcations for statechart diagrams (OMG,

2011) as inconsistent state invariants, and may cause

whole system become unsatisﬁable or inconsistent.

The examples of inconsistent state invariants are as

follows:

ConsistencyofUMLClassandStatechartDiagramswithStateInvariants

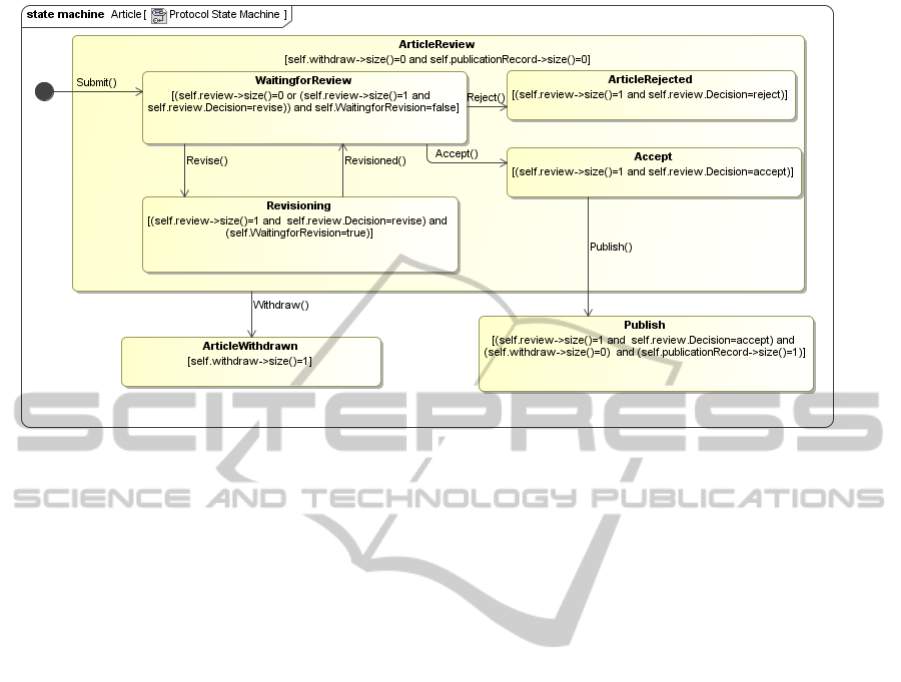
Figure 2: The behavioral view of the class Article of the class diagram shown in Figure 1.

Inconsistent State Invariant Example 1. Ac-

cording to the UML superstructure speciﬁcation,

invariants of non-orthogonal states must be mutu-

ally exclusive ((OMG, 2011), p.564), for example

in the statechart diagram shown in Figure 2, the

article cannot be in the state of ArticleRe jected

if at the same time this article is in the state of

Accept. If we introduce an error by changing

the invariant value of the state ArticleRe jected to

self.review->size()=1 and self.review.Dec-

ision=accept, means that an article can be rejected

and accepted at the same time. The introduced

error allows an object of the class Article to be-

long to two non-orthogonal states i.e. Accept and

ArticleRe jected, which is the violation of the UML

superstructure speciﬁcation of the statechart dia-

gram, and as a consequence the invariant of states

ActicleRe jected and Accept becomes inconsistent.

Inconsistent State Invariant Example 2. Accord-

ing to the UML superstructure speciﬁcation, when-

ever a state is active, all its superstates are active

((OMG, 2011), p.565), means all invariants of an

active state and its superstates directly or transi-

tively are true. For example, in a statechart dia-

gram see Figure 2, if the state Accept is active then

its superstate ArticleReview should be also active.

If we introduce an error by adding the condition

self.withdraw->size()=1 in the invariant of the

state Accept, means that a withdrawn article can also

be accepted. The introduced error causes the contra-

diction between the invariants of the state Accept and

its superstate ArticleReview, and violates the UML

superstructure speciﬁcation of the statechart diagram,

and consequently makes the invariant of the states

Accept, ArticleReview and ArticleWithdrawn incon-

sistent.

In the next section we discuss how we can carry

out the analysis of these kind of models using OWL 2

reasoning tools.

2.1 Previous Work

The consistency analysis of UML class diagrams and

statechart diagrams has been studied by a number of

researchers in the recent past, but often the analysis

has focused on different properties of a design. The

approach by Yeung et al. (Yeung, 2004) analyzes the

behavior of statecharts to ﬁnd deadlocks, by translat-

ing class diagrams into the B-Method and statechart

diagrams into CSP. This approach is not focused on

the consistency of state invariants, the translation is

done manually and there is no discussion about the

veriﬁcation method whether it is manual or automatic.

The approach by Rasch et al. (Rasch and

Wehrheim, 2003), uses Object-Z for the formaliza-

tion of class models and CSP for statechart diagrams,

this approach analyzes method invocations against the

class description and ﬁnds deadlocks by running the

class and statechart diagram formalization in FDR.

This approach is not focused on the analysis of the

consistency of state invariants. Furthermore, the ap-

proach by Lam et al. (Lam and Padget, 2005) ana-

lyzes the consistency of statechart diagrams and class

diagrams by using the π-calculus. The translation of

UML diagrams to π-calculus is done manually and

MODELSWARD2013-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

the consistency is analyzed by running the π-calculus

script on the Workbench.

Moreover, the approach by Emil Sekerinski (Sek-

erinski, 2008) focus on the veriﬁcation of statecharts.

In this approach, the events are manually translated

into generalized program statements, and these state-

ments appeared as the body of a transition. The exe-

cution of the program statements is based on the as-

sumption that the body of the transition can read or

write the values of the class variables.

The use of ontology languages and description

logic in the context of model validation has been

proposed in the past by different authors (Van

Der Straeten, 2005; Wang et al., 2006; Berardi et al.,

2005; Balaban and Maraee, 2008). However, to our

knowledge, none of them has addressed the reasoning

of the satisﬁability of state invariants using OWL 2

DL. These works focus on the problem of class di-

agrams satisﬁability, i.e., a class diagram can gener-

ate consistent object diagrams or not. Moreover, the

approach by Moaz et al. (Maoz et al., 2011), ana-

lyzes the consistency of class and object diagrams by

using Alloy. This is a fully automatic approach, in

this approach the class and object diagrams are ﬁrst

translated into a parameterized Alloy module, and

then the consistency analysis is done by analyzing

the translated Alloy module by using the Alloy An-

alyzer. This approach do not yet supports statecharts

and OCL constraints. Furthermore, the TWOUSE ap-

proach (Walter et al., 2012) is focused on two areas,

ﬁrst is the Ontology Development Modeling (ODM),

and the second is the translation and validation of Do-

main Speciﬁc Languages (DSL) by using OWL 2.

This approach proposes same methodology for the

validation of DSLs as presented in this article. How-

ever, their work on validation is limited to the valida-

tion of DSLs, and has not yet offered the validation of

statechart diagrams with or without state invariants.

Furthermore, Bogumila et al. (Hnatkowska et al.,

2001), analyze the consistency of the statechart dia-

gram of a class by writing OCL rules manually, and

then execute the OCL rules by using the OCL com-

piler. This approach is limited to analyzing consis-

tency of statechart diagrams against the class descrip-

tion and not using state invariants. In OCL, the model

validation rules must be deﬁned explicitly based on

the syntax of the UML models. In our approach,

model validation is deﬁned in the semantic interpre-

tation of the OCL and UML models. The differ-

ence is that while OCL must deﬁne a large number of

well-formed rules for different variations and combi-

nations of model elements, a logic approach requires

a smaller number of axioms that are often simpler.

To our knowledge, none of the above mention

work proposes an automatic translation and consis-

tency checking approach for UML class and stat-

echart diagrams with state invariants described in

OCL.

3 CONSISTENCY ANALYSIS

In this section we deﬁne the problem of determin-

ing the consistency of UML models containing class

and statechart diagrams as follows. Our view of

model consistency is inspired by the work of Broy

et al. (Broy et al., 2009). This work considers the

semantics of a UML diagram as their denotation in

terms of a so-called system model and deﬁnes a set of

diagrams as consistent when the intersection of their

semantic interpretation is nonempty.

In our work, we assume that there is a nonempty

set ∆ called the object domain containing all the pos-

sible objects in our domain. We propose that a UML

model depicting a number of class and statechart dia-

grams is interpreted as a number of subsets of ∆ rep-

resenting each class and each state in the model and

as a number of conditions that need to be satisﬁed by

these sets.

A UML class is represented a set C, such C ⊆ ∆.

An object o belongs to a UML class C iff o ∈ C. We

also represent each state S in a statechart as a subset

of our domain S ⊆ ∆. In this interpretation, the state

set S represents all the objects in the domain that have

such state active, that is, object o is in UML state S iff

o ∈ S.

Other elements that can appear in a UML model

such as generalization of classes, association of

classes, state hierarchy and state invariants are inter-

preted as additional conditions over the sets represent-

ing classes and states. For example class specializa-

tion is interpreted as a condition stating that the set

representing a subclass is a subset of the set repre-

senting its superclass. These conditions are described

in detail in the next section.

In this interpretation, the problem of a UML

model consistency is then reduced to the problem of

satisﬁability of the conjunction of all the conditions

derived from the model. If such conditions cannot

be satisﬁed, then a UML model will describe one or

more UML classes that cannot be instantiated into ob-

jects or objects that cannot ever enter a UML state in a

statechart. This can be considered a design error, ex-

cept in the rare occasion that a designer is purposely

describing a system that cannot be realized. To ana-

lyze the UML models and discover possible inconsis-

tencies we will use the services of an OWL 2 reason-

ing tool, as described in the rest of this section.

ConsistencyofUMLClassandStatechartDiagramswithStateInvariants

3.1 Description Logic and OWL 2

The Description Logic used in our approach is classi-

ﬁed as S R OI Q (Horrocks et al., 2006). Description

Logic is made up of concepts, denoted here by C, D,

and roles, denoted here by R,Q. A concept or role can

be named, also called atomic, or it can be composed

from other concepts and roles.

An interpretation I consists of a non-empty set

∆

and an interpretation function which assigns a set

⊆ ∆

to every named concept C and a binary rela-

tion R

⊆ ∆

× ∆

to every named role R.

The constructors of Description Logic are as fol-

lows:

Everything >

= ∆

Nothing ⊥

Complement (¬C)

= ∆

Inverse (R

−

)

= {(y, x) | (x, y) ∈ R

}

Intersection (C u D)

= C

∩ D

Union (C t D)

= C

∪ D

Restriction

Universal (∀R.C)

= {x | ∀y.(x, y) ∈ R

→ y ∈ C

}

Existential (∃R.C)

= {x | ∃y.(x, y) ∈ R

∧ y ∈ C

}

Cardinality (≥ nR)

= {x | #{y | (x, y) ∈ R

} ≥ n}

(≤ n R)

= {x | #{y | (x, y) ∈ R

} ≤ n}

where #X is the cardinality of X. The axioms in DL

can be either inclusions C v D, C v D or equalities

C ≡ D, R ≡ Q.

An interpretation satisﬁes an inclusion C v D if

⊆ D

and an inclusion R v Q if R

⊆ Q

. An in-

terpretation satisﬁes an equality C ≡ D if C

= D

and

an equality R ≡ Q if R

= Q

. I satisﬁes a set of ax-

ioms if it satisﬁes each axiom individually – I is then

said to be a model of the set of axioms. Given a set

of axioms K , a named concept C is said to be satisﬁ-

able if there exists at least one model I of K in which

0. A set of axioms is said to be satisﬁable if all

of the named concepts that appear in the set are satis-

ﬁable. If a set of axioms K is satisﬁable, we say that

an axiom φ is satisﬁable with respect to K if K ∪{φ}

is satisﬁable. Similarly, we say that φ is unsatisﬁable

(w.r.t. K ) if K ∪ {φ} is unsatisﬁable.

The decidability of SR OI Q is demonstrated by

Horrocks et al. (Horrocks et al., 2006).

3.2 OWL 2 Functional Syntax

For practical reasons, we use the OWL 2 functional

syntax (OWL2fs) (W3C, 2009b) as the language used

as an input for the reasoners and in the text of this

article. The interpretation of the main OWL 2 expres-

sions used in this article is presented in the follow-

ing table. A complete description of the OWL 2 se-

mantics, including support for data types can be found

in (W3C, 2009a).

SubClassOf(C D) C v D

EquivalentClasses(C D) C ≡ D

DisjointClasses(C D) C u D =

ObjectPropertyDomain(R C) ∀R

−1

ObjectPropertyRange(R C) ∀R.C

ObjectMinCardinality( n R) ≥ nR

ObjectMaxCardinality( n R) ≤ nR

ObjectExactCardinality(n R) (≥ nR) u (≤ n R)

3.3 Reasoning

In order to determine the satisﬁability of the concepts

represented in a UML model, we propose to represent

the UML model using a Description Logic, and ana-

lyze the satisﬁability of the concepts using automated

reasoning tools. We have chosen OWL 2 DL to rep-

resent our UML models since we consider it is well

supported and adopted, and there exist several OWL 2

reasoners (Sirin et al., 2007; Shearer et al., 2008;

Tsarkov and Horrocks, 2006) for analyzing concept

satisﬁability. A number of UML class diagrams, stat-

echart diagrams and state invariants are taken as an

input. All the inputs are translated to OWL 2 DL, and

then analyzed by a reasoner. The reasoner provides a

report of unsatisﬁable and satisﬁable concepts. Unsat-

isﬁable concepts will reveal UML classes that cannot

be instantiated or UML states that cannot be entered.

In the next section, we discuss and translate the

structure of UML models with state invariants, and

the UML superstructure speciﬁcation conditions over

the sets representing classes and states into OWL 2

DL.

4 FROM CLASS AND

STATECHART DIAGRAMS TO

OWL 2 DL

4.1 From Class Diagram to OWL 2 DL

According to the UML superstructure speciﬁcation, a

UML class diagram is a set of classes and their rela-

tionships in form of associations and generalizations

((OMG, 2011), p.144). In order to analyze the consis-

tency of UML class diagrams, we need to ﬁrst trans-

late all classes and their associations into OWL 2 on-

tology, and then validate the OWL 2 ontology using

an OWL 2 reasoner. In this section we only present

the translation of those class diagram concepts which

MODELSWARD2013-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

are required for the validation of statechart diagrams

with state invariants such as: class, association, mul-

tiplicity, attributes and enumeration. All OWL 2 DL

translations we discuss in this section are based on

the Description Logic interpretation of UML concepts

given in (Van Der Straeten, 2005; Wang et al., 2006;

Maoz et al., 2011; Berardi et al., 2005; Balaban and

Maraee, 2008; Walter et al., 2012).

4.1.1 Class

A class in a class diagram represents a collection of

objects which share the same features, constraints and

deﬁnition. Each class in a class diagram is treated as

a class in OWL 2. A UML class C is translated in

OWL 2 as Declaration(Class(C)).

4.1.2 Objects Belong to a Class also Belong to its

Superclass

Class specialization is reduced to the

concept inclusion. We represent the

fact that a UML class C1 is a spe-

cialization of UML class C2 with the

condition C

v C

. In this case we

say that C2 is a superclass of C1. If C2 is a superclass

of C1 we say that they are in a specialization rela-

tion. The specialization relation C

v C

is translated

in OWL 2 as SubClassOf( C1 C2 ).

4.1.3 If an Object Belongs to Multiple Classes,

they are Related by Specialization

We assume that an object cannot belong to two dif-

ferent classes, except when these two classes are in a

specialization relation. In our semantic interpretation

of a UML class diagram, it is important to denote the

fact that two classes are not in a specialization rela-

tion.

We represent the fact that UML class C1 and UML

class C2 are not in a specialization relation with the

condition C

u C

=⊥. With this condition, an ob-

ject cannot belong to these two classes simultane-

ously. Due to the open-world assumption used in De-

scription Logic, we need to explicitly state this fact in

OWL 2 as DisjointClasses( C1 C2 ).

4.1.4 Association

We represent a UML directed binary association A

from class C1 to C2 as a relation A : C

. An as-

sociation of a UML class in a class diagram is anno-

tated with a positive number; this number indicates

the multiplicity of an association. Association multi-

plicity describes a number of allowable objects of a

range class to link with the object of a domain class.

The multiplicity of an association deﬁnes additional

conditions over this relation #{y|(x, y) ∈ A} ≥ min,

#{y|(x, y) ∈ A} ≤ max.

min..max

A UML association A from

UML class C1 to C2 and have a

multiplicity (min, max) is repre-

sented in OWL 2 as:

Declaration(ObjectProperty(A))

ObjectPropertyDomain( A C1 )

ObjectPropertyRange( A C2 )

SubClassOf( C1

ObjectMinCardinality( min A ) )

SubClassOf( C1

ObjectMaxCardinality( max A ) )

4.1.5 Attributes

+Att1: Integer

+Att2: String

+Att3: Date

+Att4: Boolean

+Att4: Enum

Attributes containing data such as

integer or boolean are also repre-

sented as relations. In this case

the range of the relation A be-

longs to the set D represents the

datatype ∀x, y : (x, y) ∈ A =⇒ y ∈ D. Also, at-

tributes usually have a multiplicity restriction to one

value. The attributes of a UML class in a class dia-

gram are translated in OWL 2 as a DataProperty. In

OWL 2, the data property use datatype in its range.

The datatype can be xsd:boolean, xsd:string, xsd:int

and other datatypes see ((W3C, 2009b), Table 3). We

map attributes that use basic types by declaring a data

property with the attribute’s name. Also, an attribute

is a required component of its class. Consequently,

the data properties describing attributes have an ex-

act cardinality of one. The attribute Att of the UML

class C having any of the above mentioned DataType

is translated in OWL 2 as:

Declaration(DataProperty( Att ))

SubClassOf(C DataExactCardinality(1 Att ))

DataPropertyDomain( Att C )

DataPropertyRange( Att DataType )

4.1.6 Enumeration

«enumeration»

Enum

literal_1

literal_n

Enumeration is a kind of the

datatype, whose instances are

a user-deﬁned enumeration

literals ((OMG, 2011), p.67).

The enumeration Enum is declared by using a

DatatypeDefinition axiom in OWL 2 DL. The

class attribute Att having a datatype Enum, means

∀x, y : (x, y) ∈ Att =⇒ y ∈ Enum where Enum is a

set of enumeration literals {(literal

), ...,(literal

)}

is represented in OWL 2 as:

ConsistencyofUMLClassandStatechartDiagramswithStateInvariants

DataPropertyRange(Att DataOneOf(

"literal1"ˆˆdatatype ..))

4.2 From Statechart Diagrams to

OWL 2 DL

A statechart diagram provides the behavioral interface

of a class and deﬁnes the sequence of method invoca-

tions, the conditions under which they can be invoked

and their expected results. In order to analyze the sat-

isﬁability of state invariants in a statechart diagram,

we need to translate the states and their invariants into

OWL 2 DL. The translation of the state and the state

invariant includes the reference of the class and its at-

tributes. Therefore, we translate a statechart diagram

in the same ontology that contains the OWL 2 trans-

lation of a class diagram.

4.2.1 State and State Hierarchy

We represent a UML state as a concept represent-

ing the objects that have such state active. A con-

cept representing a state will be included in the con-

cept representing all object instances of the class as-

sociated to the statechart diagram, since all objects

that can have the state active belong to the given

class. That is, if the state S belongs to a statechart

diagram describing the behavior of the class C, then

S v C. We represent this in OWL 2 as follows:

sub

Declaration(Class(S))

SubClassOf( S C )

State hierarchy is also represented using a concept in-

clusion. Whenever a substate is active, its containing

state is also active. This implies that the concept rep-

resenting a substate will be included in the concept

representing is the parent state, sub v S. This is rep-

resented in OWL 2 as SubClassOf( sub S ).

4.2.2 Non-orthogonal States are Exclusive

S1 S2

The UML Superstructure

speciﬁcation requires that if

a composite state is active

and not orthogonal, at most one of its substates is

active ((OMG, 2011), p.564). This means that an

object cannot be at the same time in the two concepts

representing two exclusive states, i.e., if S

and S

represents substates of an active and not orthogonal

composite state then S

u S

=⊥. When representing

a statechart diagram in OWL 2, the non-orthogonal

exclusive states are declared as disjoint, so that they

may not able to share any object.

DisjointClasses( S1..Sn )

4.2.3 Orthogonal States are Non-exclusive

R1 R2

S2S1

The UML Superstructure

speciﬁcation requires that if

a composite state is active

and orthogonal, all of its regions are active ((OMG,

2011), p.564). That is if R

and R

are concepts rep-

resenting the two regions of an orthogonal composite

state represented by the concept S, then R

t R

= S.

We should note that if S

and S

represent two

substates where S

v R

and S

v R

, then they are

not exclusive and S

u S

6=⊥. Due to the open-world

assumption of DL, concepts may represent common

individuals unless they are explicitly declared as

disjoint.

4.3 State Invariant into OWL 2 DL

The UML speciﬁcation deﬁnes a state in a UML

diagram as the representation of a speciﬁc con-

dition “A state models a situation during which

some (usually implicit) invariant condition holds”

((OMG, 2011), p.559-560). We understand from

this deﬁnition that the invariant condition charac-

terizes the state: if the invariant condition holds

the state is active, otherwise if the invariant con-

dition does not hold the state is not active.

Invariant

In our approach we represent

an invariant as an OWL 2 con-

cept representing objects that

make that invariant evaluate to true. Since the invari-

ant holds iff the associated state is active, the con-

cept representing a state will be the same as the con-

cept representing an invariant. This is represented in

OWL 2 as an equivalent class relation between the

state and its invariant:

EquivalentClasses (S Invariant)

Due to the equivalent relationship between the state

and its invariant, all objects that fulﬁll the condition

of its state invariant will also be in that speciﬁc state.

4.3.1 State Constraints

The UML also allows us to deﬁne additional con-

straints to a state, and names these constraints also

state invariants. However, the semantics of a state

constraint are more relaxed since it “speciﬁes condi-

tions that are always true when this state is the current

state” ((OMG, 2011), p.562). In this sense, the state

constraints deﬁne necessary conditions for a state to

be active, but not sufﬁcient. This means that, the ac-

tual state invariant may remain implicit. However, we

consider a state invariant as a predicate characterizing

MODELSWARD2013-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

a state. That is, a state will be active if and only if its

state invariant holds.

4.3.2 A State Invariant Characterizes a State

The UML superstructure speciﬁcation requires that

whenever a state is active its state invariant evaluates

to true ((OMG, 2011), p.562). A consequence of this

is that state invariants should be satisﬁable. That is,

every state invariant in a statechart diagram must hold

in at least one object conﬁguration. Otherwise there

cannot be objects that have such state active. Since

invariants should be satisﬁable, the concept S repre-

senting a state should be satisﬁable S 6=⊥.

4.4 OCL to OWL 2 DL

A state invariant is a runtime constraint on a state in

a statechart ((OMG, 2011), p.514). The UML speci-

ﬁcation proposes the use of OCL to deﬁne constraints

in UML models, including state invariants. OCL is

well supported by many modeling tools (Birgit De-

muth, 2009; Garcia and Shidqie, 2007). Unfortu-

nately, in general OCL is not decidable. However, we

can avoid undecidability by restricting our approach

to a reduced fragment of the full OCL (Queralt et al.,

2012a). The use of a limited fragment of OCL to

avoid undecidability has been proposed in the past

also by other authors (Queralt et al., 2012a; Queralt

et al., 2012b).

In this article, we consider OCL constructs using

mainly multiplicity, attributes value and boolean op-

erators. The grammar of OCL, supported in our ap-

proach is shown in Figure 3.

4.4.1 Attribute Constraints

State

{self.Att=Value}

The value of the attribute is

accessed in OCL by using a

keyword sel f or by using a

class reference ((OMG, 2006), p.15), the value

constraint of the attribute Att is written in OCL

as self.Att=Value, meaning {x|(x,Value) ∈ Att},

where Value represents the attribute value. The re-

striction on the value of the attribute is translated in

OWL 2 by using the axiom DataHasValue. The OCL

attribute value constraint self.Att=Value is trans-

lated in OWL 2 as:

DataHasValue(Att "Value"ˆˆdatatype )

In above translation, Att is the name of the attribute,

Value is the value of the attribute and it is always writ-

ten in OWL 2 in double quotes, and datatype is the

datatype of the attribute Value.

4.4.2 Multiplicity Constraints

State

{self.A-->size()=Value}

The multiplicity of an as-

sociation is accessed by us-

ing size() operation in OCL

((OMG, 2006), p.144). The multiplicity con-

straint on the association A in OCL is written as

self.A->size()=Value, where Value is a posi-

tive integer and represents a number of allowable in-

stances of the range class of the association A. We can

use a number of value restriction inﬁx operators with

size() operation such as =, >=, <=, < and >. The

multiplicity constraint on an association A is deﬁned

as {x|#{y|(x, y) ∈ A}OP Value}, where OP is the inﬁx

operator and Value is a positive integer. The transla-

tion of size() operation in OWL 2 is based on the in-

ﬁx operator used with the size() operation, for exam-

ple, the OCL constraint self.A->size()=Value, in

which A is the name of an association, ”>” is an inﬁx

operator and Value is a positive integer, translated in

OWL 2 as: ObjectExactCardinality(Value A).

Furthermore, the constructs isEmpty and

notEmpty represent size() = 0 and size() > 0 re-

spectively. The invariant self.A->isEmpty() is

translated in OWL 2 as:

ObjectExactCardinality(0 A)

and the invariant self.A->notEmpty() is translated

in OWL 2 as:

ObjectMinCardinality(1 A)

4.4.3 Boolean Operators

State

{self.Att=Value and

self.A->size()=Value}

The constraints in a state in-

variant are written in a form

of a boolean expression, and

joined by using the boolean operators, such as ”and”

and ”or” ((OMG, 2006), p.144). The binary ”and”

operator evaluates to true when both boolean ex-

pressions Ex

and Ex

are true. In our transla-

tion this is represented by the intersection of the

concepts that represent both expressions Ex

∩ Ex

as ObjectIntersectionOf(Ex1 Ex2). The binary

”or” operator evaluates to true when at least one of the

boolean expression Ex

or Ex

is true. In our trans-

lation this is represented by the union of the concepts

that represent both expressions Ex

tEx

. This is rep-

resented OWL 2 as ObjectUniounOf(Ex1 Ex2).

ConsistencyofUMLClassandStatechartDiagramswithStateInvariants

hOCL-expressioni ::= hcond-expri (hlogic-opihcond-expri)

∗

hlogic-opi ::= and | or

hcond-expri ::= hrefi →size()hrelational-operatorihinteger-literali

| hrefi →isEmpty() | hrefi → notEmpty()

| hrefihrelational-operatorihprimitive-literali

hrefi ::= self.hidentiﬁeri

hidentiﬁeri ::=

{hcharactersi} | 0..9 {0..9}

hrelational-operatori ::= < | <= | > | >= | <> | =

hprimitive-literali ::= hboolean-literali | hinteger-literali

| hstring-literali | null

hboolean-literali ::= true | false

hinteger-literali ::= 0..9 {0..9}

hstring-literali ::=

{hcharactersi}

Figure 3: The grammar of the supported OCL fragment.

// Class Diagram into OWL 2 DL

Declaration(Class(Article))

Declaration(Class(Review))

Declaration(Class(Withdraw))

Declaration(Class(PublicationRecord))

...

DisjointClasses( Article Review ...)

Declaration(ObjectProperty(review))

ObjectPropertyDomain( review Article)

ObjectPropertyRange( review Review )

...

SubClassOf( Article

ObjectMaxCardinality( 1 review ))

....

Declaration(

DataProperty( WaitingforRevision))

SubClassOf(Article

DataExactCardinality(1 WaitingforRevision))

...

DataPropertyDomain(

WaitingforRevision Article )

DataPropertyRange(

WaitingforRevision xsd:boolean )

//Statechart diagram into OWL 2 DL

Declaration(Class(ArticleReview))

Declaration(Class(ArticleWithdraw))

Declaration(Class(Publish))

SubClassOf( ArticleReview Article )

SubClassOf( ArticleWithdraw Article )

SubClassOf( Publish Article ))

...

DisjointClasses( ArticleReview

ArticleWithdraw Publish )

Declaration(Class(WaitingforReview))

SubClassOf( WaitingforReview ArticleReview )

...

//Invariant of state Publish Start

EquivalentClasses (Publish

ObjectIntersectionOf(

ObjectExactCardinality(1 review)

DataHasValue(Decision "accept"ˆˆxsd:string ))

ObjectIntersectionOf ( ObjectExactCardinality

(0 withdraw) ObjectExactCardinality

(1 publicationRecord)) ) )

//Invariant of state Publish End

Figure 4: The excerpt of the output ontology generated by the translation tool.

5 CONSISTENCY ANALYSIS

USING AN OWL 2 REASONING

TOOL

We have deﬁned earlier the satisﬁability of UML

models in Section 3. The consistency analysis of

UML models is reduced to the satisﬁability of the

conjunction of all conditions derived from a model.

In order to determine the satisﬁability of the condi-

tions represented in UML models, we ﬁrst translate

the UML models into an OWL 2 ontology, then use an

OWL 2 reasoner to analyze the satisﬁability of trans-

lated concepts.

To translate UML models into OWL 2 ontology,

we have implemented the translations of class dia-

grams, statechart diagrams and state invariants dis-

cussed in Section 4, in an automatic model to text

transformation tool. The implemented translation

tool allows us to automatically translate class dia-

grams, statechart diagrams and state invariants into

OWL 2 DL. The translator reads class diagrams, stat-

echart diagrams and OCL state invariants from an in-

put model serialized using the XMI format. The XMI

MODELSWARD2013-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

Found 4 unsatisfiable concept(s):

a:Accept

a:ArticleRejected

a:ArticleReview

a:ArticleWithdrawn

Figure 5: The satisﬁability report of the ontology shown in

Figure 4 generated by the OWL 2 reasoner Pellet.

is generated by using a modeling tool. We used Mag-

icdraw to create the example designs used in this arti-

cle. The output of the translation tool is an ontology

ﬁle ready to be processed by an OWL 2 reasoner.

As an example, we have translated the class di-

agram, statechart diagram and OCL state invariants

shown in Figure 1 and Figure 2, into OWL 2 DL on-

tology using the implemented translation tool. An ex-

cerpt of the output ontology generated by the transla-

tion tool is shown in Figure 4.

5.1 Reasoning

After translating the class diagram, statechart diagram

and state invariants into an OWL 2 ontology by us-

ing the implemented translation tool, we process the

ontology by using an OWL 2 reasoner. The OWL 2

reasoner combines all the facts presented as axioms

in the ontology and infers logical consequences from

them. When we give the generated ontology to the

reasoner, it generates a satisﬁability report indicat-

ing which concepts are satisﬁable and which not. If

the ontology has one or more unsatisﬁable concept,

this means that the instance of any unsatisﬁable con-

cept will make the whole ontology inconsistent, con-

sequently, an instance of the class describing an un-

satisﬁable concept in a class diagram will not exist, or

objects will not enter into a state describing an unsat-

isﬁable condition, otherwise viceversa.

In order to analyze the satisﬁability of the incon-

sistent invariants listed in Section 2. The ontology of

an example model with inconsistent invariants is vali-

dated by using an OWL 2 reasoner name Pellet (Sirin

et al., 2007). The satisﬁability report of the ontology

of UML models with inconsistent state invariants is

shown in Figure 5. As explained in Section 4.3, a

state invariant characterizes the state ((OMG, 2011),

p.559-560). Therefore, the presence of unsatisﬁable

states in the satisﬁability report indicates the existence

of inconsistent state invariants in identiﬁed states.

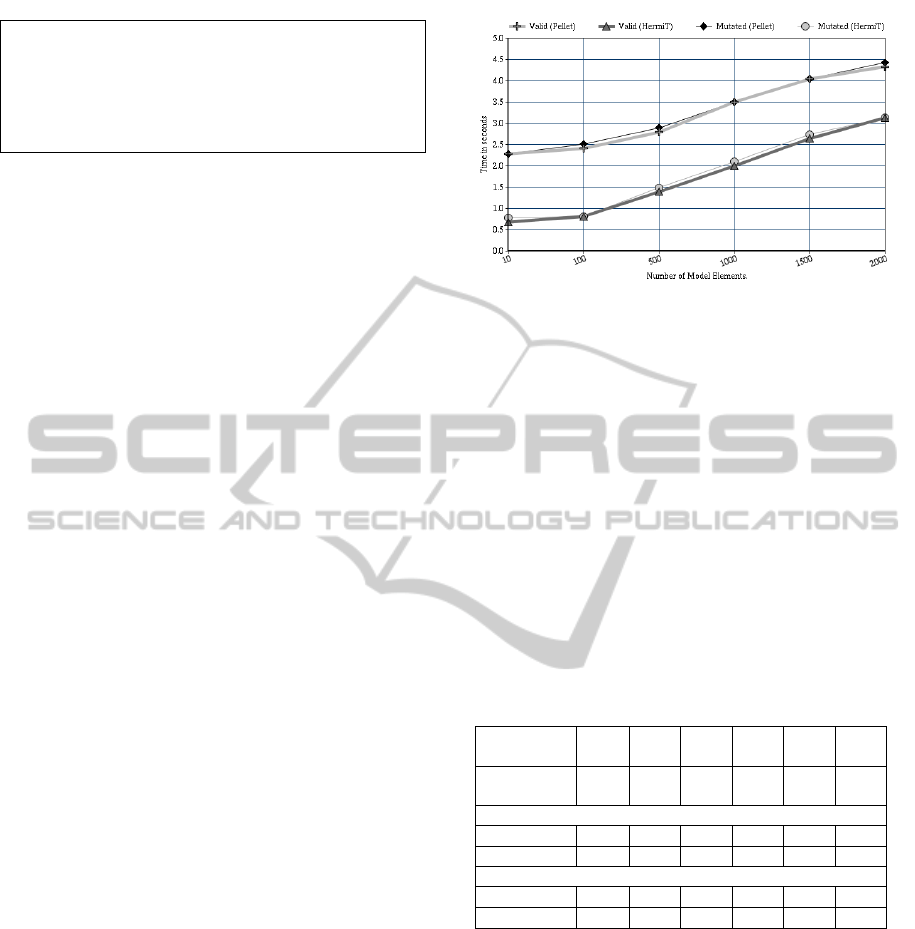
5.2 Performance Analysis

In order to determine the performance of the transla-

tion and reasoning tools, we conducted an experiment

Figure 6: The graph of the total time (Translation time +

Reasoning time) to process valid and mutated models.

using UML class and statechart diagrams consisting

of 10 to 2000 model elements. We use a desktop com-

puter with an Intel Core 2 Duo E8500 processor run-

ning at 3.16GHz with 2GB of RAM. The performance

tests are conducted for both consistent and mutated

models containing inconsistencies introduced by us.

For each test, we measure the time required to trans-

late a model from UML to OWL 2 and the time re-

quired by the OWL 2 reasoners Pellet (Sirin et al.,

2007) and HermiT (Shearer et al., 2008) to analyze

the models. The results are shown in Table 1, and in

Figure 6.

Table 1: Time taken by the translation tool and rea-

soning engines to process UML models.

Model El-

ements

10 100 500 1000 1500 2000

Translation

Time

0.08s 0.11s 0.19s 0.30s 0.44s 0.53s

Pellet

Valid 2.2s 2.3s 2.6s 3.2s 3.6s 3.8s

Mutated 2.2s 2.4s 2.7s 3.2s 3.6s 3.9s

HermiT

Valid 0.6s 0.7s 1.2s 1.7s 2.2s 2.6s

Mutated 0.7s 0.7s 1.3s 1.8s 2.3s 2.6s

The time complexity of OWL 2 DL with respect

to the reasoning problems of the ontology consistency

and instance analyzing is NEXPTIME complete (Hor-

rocks et al., 2003). However, the graph (Figure 6) of

the performance test shows that the time required to

reason about models only grows linearly. This is due

to the fact that in our approach we analyze the con-

sistency of class and statechart diagrams without in-

dividuals.

6 CONCLUSIONS

In this article we have presented an approach to an-

ConsistencyofUMLClassandStatechartDiagramswithStateInvariants

alyze the consistency of UML class diagrams and

UML statechart diagrams with state invariants. The

approach is fully automated thanks to the translation

tool and the existing OWL 2 reasoners. Since the

translation tool accepts standard UML models seri-

alized using the XMI standard, the approach can be

easily integrated with existing UML modeling tools.

Our approach is decidable because we restrict our-

selves to an admittedly small fragment of OCL. This

strategy has been already used for expressing con-

straints over class diagrams (Cabot et al., 2008; Quer-

alt et al., 2012b). We believe that the use of limited

subsets of OCL do not reduce the merits of this and

similar approaches even if they cannot be used to pro-

cess all possible OCL constraints. An analysis tool

could in fact integrate different analysis approaches

and use the right one depending of the fragment of

OCL used in the models.

The performance experiments show that the pro-

posed approach can process relatively large UML

models in few seconds by using current reasoning

tools on desktop computers. Therefore, we consider

that this approach has the potential to be incorporated

with existing and future UML modeling tools and of-

fer consistency analysis services that go ahead of what

is being offered in current modeling tools.

REFERENCES

Balaban, M. and Maraee, A. (2008). A UML-based method

for deciding ﬁnite satisﬁability in description logics.

In Description Logics.

Berardi, D., Calvanese, D., and Giacomo, G. D. (2005).

Reasoning on UML class diagrams. Artif. Intell.,

168(1-2):70–118.

Birgit Demuth, C. W. (2009). Model and Object Veriﬁ-

cation by Using Dresden OCL. In Proceedings of

the Russian-German Workshop Innovation Informa-

tion Technologies: Theory and Practice,, pages 81–

89.

Broy, M., Cengarle, M. V., Gr

onniger, H., and Rumpe, B.

(2009). Considerations and Rationale for a UML Sys-

tem Model. In UML 2 Semantics and Applications,

pages 43–60. John Wiley & Sons, Hoboken.

Cabot, J., Clariso, R., and Riera, D. (2008). Veriﬁcation of

UML OCL class diagrams using constraint program-

ming. ICSTW, pages 73–80.

Garcia, M. and Shidqie, A. J. (2007). OCL Compiler for

EMF. In Eclipse Modeling Symposium at Eclipse

Summit Europe 2007, Stuttgart, Germany.

Hnatkowska, B., Huzar, Z., and Magott, J. (2001). Consis-

tency Checking in UML Models. In ISM’01.

Horrocks, I., Kutz, O., and Sattler, U. (2006). The even

more irresistible SROIQ. In KR, pages 57–67.

Horrocks, I., Peter, F., Schneider, P., and Harmelen, F. V.

(2003). From SH I Q and RDF to OWL: The mak-

ing of a web ontology language. J. of Web Semantics,

1(1):7–26.

Lam, V. S. W. and Padget, J. A. (2005). Consistency check-

ing of statechart diagrams of a class hierarchy. In

ECOOP, pages 412–427.

Maoz, S., Ringert, J. O., and Rumpe, B. (2011). Seman-

tically conﬁgurable consistency analysis for class and

object diagrams. In MoDELS, pages 153–167.

OMG (2006). OCL, OMG Available Speciﬁcation, Version

2.0. http://www.omg.org/spec/OCL/2.0/.

OMG (2011). UML, Superstructure Speciﬁcation, Ver-

sion 2.4.1. http://www.omg.org/spec/UML/2.4.1/

Superstructure/.

Queralt, A., Artale, A., Calvanese, D., and Teniente, E.

(2012a). OCL-Lite: A decidable (yet expressive)

fragment of OCL. In Proc. of the 25th Int. Work-

shop on Description Logics (DL 2012), volume 846 of

CEUR Electronic Workshop Proceedings, http://ceur-

ws.org/, pages 312–322.

Queralt, A., Artale, A., Calvanese, D., and Teniente, E.

(2012b). OCL-Lite: Finite Reasoning on UML/OCL

Conceptual Schemas. Data and Knowledge Engineer-

ing, 73:1–22.

Rasch, H. and Wehrheim, H. (2003). Checking consis-

tency in uml diagrams: Classes and state machines. In

FMOODS 2003, volume 2884 of LNCS, pages 229–

243. Springer Berlin / Heidelberg.

Sekerinski, E. (2008). Verifying statecharts with state in-

variants. In ICECCS, pages 7–14.

Shearer, R., Motik, B., and Horrocks, I. (2008). HermiT: a

highly-efﬁcient OWL reasoner. OWLED.

Sirin, E., Parsia, B., Grau, B. C., Kalyanpur, A., and Katz,

Y. (2007). Pellet: A practical OWL-DL reasoner.

Journal of Web Semantics, 5:51–53.

Tsarkov, D. and Horrocks, I. (2006). Fact++ description

logic reasoner: system description. In Proceedings of

the Third international joint conference on Automated

Reasoning, IJCAR’06, pages 292–297, Berlin, Hei-

delberg. Springer-Verlag.

Van Der Straeten, R. (2005). Inconsistency Management

in Model-driven Engineering. An Approach using De-

scription Logics. PhD thesis, Vrije Universiteit Brus-

sel, Brussels, Belgium.

W3C (2009a). OWL 2 Web Ontology Language Di-

rect Semantics. http://www.w3.org/TR/owl2-direct-

semantics/.

W3C (2009b). OWL 2 Web Ontology Language

Structural Speciﬁcation and Functional-Style Syn-

tax. http://www.w3.org/TR/2009/REC-owl2-syntax-

20091027/.

Walter, T., Parreiras, F., and Staab, S. (2012). An ontology-

based framework for domain-speciﬁc modeling. Soft-

ware and Systems Modeling, pages 1–26.

Wang, S., Jin, L., and Jin, C. (2006). Ontology deﬁnition

metamodel based consistency checking of UML mod-

els. In CSCWD 2006, pages 1–5.

Yeung, W. L. (2004). Checking Consistency between UML

Class and State Models Based on CSP and B. J. UCS,

10(11):1540–1559.

MODELSWARD2013-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment