Incorporating Proofs in a Categorical Attributed Graph Transformation

System for Software Modelling and Veriﬁcation

∗

Bertrand Boisvert, Louis F´eraud and Sergei Soloviev

IRIT, Universit´e Paul Sabatier, Toulouse, France

Keywords:

Model Transformation, Graph Transformation, Attribute Computation, Single Pushout.

Abstract:

This paper deals with model transformations based on attributed graphs transformation. Our approach is

based on the categorical approach called Single Pushout. The principal goal being to strengthen the attribute

computation part, we generalize our earlier approach based on the use of typed lambda-terms with inductive

types and recursion to represent attributes and computation functions. The generalized approach takes terms in

variable context as attributes and partial proofs as computation functions that permit to combine computation

with proof development and veriﬁcation. The intended domains of application are the development of ceriﬁed

software models and semantics models for interactive proof development and veriﬁcation.

1 INTRODUCTION

In Model Driven Engineering (abbreviated MDE),

models are mostly described using a graphical syntax

(UML, SDL, etc.). Models are composed of a struc-

tural part which can be represented as a graph and of

attributes which are informations attached to vertices

or edges of the graph. Thus, models can be formal-

ized as attributed graphs and model transformation as

attributed graph transformations. An attributed graph

transformation is composed of a rewrite of the struc-

tural part and of computations on its attributes.

When consideringgraph transformations,it can be

noticed that a lot of them deal onlywith structures and

not with attributes. For instance transforming UML

class diagrams to relational models or UML activity

diagrams to Petri nets require few attribute compu-

tations. In contrast, when dealing with formalisms

such as timed automata, complex Petri nets (predicate

Petri nets, Object Petri nets, colored Petri nets), in-

ternal program representation leads to sophisticated

attribute computations. In our previous and current

works we decided to focus on graph transformations

requiring complex computations. So we developped

a ﬁrst approach based on a typed λ-calculus and now

we moved a step further considering inference rules

as a way to make attribute computations.

One of the challenges of attributed graph transfor-

mation systems concerns the implementation of at-

∗

Part of this research has been supported by the Climt

project, ANR-11-BS02-016-02

tribute computations. Most of the existing systems

based on category theory adopt the standard algebraic

approach where graphs are attributed using algebraic

data types represented by Σ-algebras (Ehrig et al.,

2006b), (Orejas, 2011). However, the computation

with algebraic data types does not permit to repre-

sent certain computations (like computation of recur-

sive functionsor term matching),and meets efﬁciency

problems when implemented.

In our earlier work, see (Rebout et al., 2011), (Re-

bout et al., 2008), (Tran et al., 2010) we suggested

to use inductive types and lambda terms in com-

bination with a modiﬁcation of the double pushout

approach (Rozenberg, 1997) called DPoPb (“double

pushout-pullback” approach). As stated above, our

goal was to use a well developed approach to imple-

ment rewriting of the structural part of graphs and

to use the expressive power of λ-terms and induc-

tive types to describe and facilitate attribute compu-

tations. But the construction of the double pushout

imposed strong constraints on computation functions

mostly due to the usage of total maps and the obli-

gation to split all the computations into two parts.

That is why later we presented a new approach based

on single pushout and λ-terms as computation func-

tions (Boisvert et al., 2011a).

In this paper, we generalize this approach towards

models incorporating proofs. Instead of λ-terms in

the same ﬁxed context we consider full typing judge-

ments of the form Γ ⊢ t : A where Γ is a context, t is

a term and A is a type. Instead of λ-terms as com-

Boisvert B., Féraud L. and Soloviev S..

Incorporating Proofs in a Categorical Attributed Graph Transformation System for Software Modelling and Veriﬁcation.

DOI: 10.5220/0004321200620074

In Proceedings of the 1st International Conference on Model-Driven Engineering and Software Development (MODELSWARD-2013), pages 62-74

ISBN: 978-989-8565-42-6

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

putation functions we take partial proofs in the corre-

sponding system of type theory. As a result, the scope

of the approach is considerably extended. It can be

used now not only to support attribute computations

in graph transformation systems but also in computer-

assisted veriﬁcation and proof-development.

The next section of this paper introduces the main

approaches of graph rewriting based on category the-

ory, and particularly the single pushout approach on

which our approach is based. Afterwards we deﬁne

our category of attributed graphs, and then explain

how to apply a rewrite rule by the computation of

a weak pushout. Proofs are based on the ideas pre-

sented in (Boisvert et al., 2011a) but applied in more

general setting. In section 5 we present examples.

Section 6 contains an outline of future work. The pa-

per is completed by an appendix that contains a brief

description of the system of typed λ-calculus with in-

ductive types used for presentation and examples as

well as necessary notions of proof theory.

2 CATEGORICAL GRAPH

REWRITING

In graph rewriting systems based on category the-

ory, we usualy deﬁne a category whose objects are

graphs and morphisms are graph homomorphisms.

A transformation rule is composed of at least two

graphs called the left-hand side (usually noted L) and

right-hand side (usually noted R). The left-hand side

describes which subgraph a graph G must contain

in order that the transformation could be applied to

it, and the right-hand side describes how this part

will look like after the transformation. Morphisms

between left-hand side and right-hand side describe

which parts of graphs will be deleted, transformed or

added. To apply a rule to some subgraph of a larger

graph G, we need ﬁrst to embed the left-hand side as

a subgraph of G. The embedding is represented by an

inclusion L

→ G. Cf Figure 1(a) and 1(b).

There are two principal categorical approaches to

graph rewriting: double pushout (abbreviated DPo,

concieved by H. Ehrig and his colleagues (Ehrig,

1978), (Rozenberg, 1997)) and single pushout (ab-

breviated SPo, mainly developped by L¨owe (L¨owe,

1993), (Rozenberg, 1997)). The main difference is

that in DPo morphisms are total maps andin SPo mor-

phisms are partial maps. This implies different forms

of rules.

In the DPo approach a rule is deﬁned by 3 graphs

and 2 total morphisms: L

← K

→ R. The morphism l

indicates what vertices or edges should be erased (the

ones who are not in the image of l) and the morphism

r indicates what vertices or edges should be trans-

formed (those who are in K), and added (those who

are not in the image of r). The application of the rule

is done by a computation of a pushout-complement

(adding the arrows K

→ D and D

∗

→ G and then a

pushout (the arrows R

∗

→ H and D

∗

→ H). Cf Figure

1(a).

In the SPo approach, a rule is deﬁned by one par-

tial morphim L

→ R. Vertices and edges not included

in the domain of r will be deleted, the ones in the do-

main of r will be transformed and those which are not

in the image of r will be added. The application of

the rule is done by the computation of one pushout

(adding the arrows G

∗

→ H and R

∗

→ H). Cf Figure

1(b)

l r

(PO1) (PO2)

∗

G D

∗

(a) DPo approach

∗

(PO)

∗

(b) SPo approach

Figure 1: Classical categorical graph rewriting approaches.

Because not all pushout-complements necessarily

exist in the categories of graphs, there exist “applica-

tion conditions” in DPo approach. As a consequence,

rules that create dangling edges are forbidden in the

DPo approach while in SPo approach dangling edges

are removed when the rule is applied. If necessary, it

is possible to add application conditions in the SPo

approach as well. Thus the SPo approach is more

general than the DPo approach, but SPo approach re-

mained less developed due, in our opinion, mostly to

historical reasons and to the fact that computation of

pushout in categories of partial maps is more difﬁcult

than in categories of total maps.

Both approachesmet many difﬁculties on the level

of attribute computations. Our experience with the

DPoPb approach, see (Rebout et al., 2008), (Rebout

et al., 2011), (Tran et al., 2010) and the use of λ-terms

for attributes was encouraging but the construction of

IncorporatingProofsinaCategoricalAttributedGraphTransformationSystemforSoftwareModellingandVerification

a double pushout still imposed some constraints due

to the use of total maps and the obligation to split

computation into two parts. The approach based on

single pushout construction with λ-terms as attributes

that we pursued afterwards (Boisvert et al., 2011a)

was more direct and natural, free of application condi-

tions and no speciﬁc constraints on the computational

level. It permitted to strengthen attribute computa-

tions and lighten the structure rewrite. At the same

time, while the relationship between λ-calculus and

proof theory is well known (one may mention famous

Curry-Howard isomorphism), the early version of our

system could not be used directly in proof develop-

ment and veriﬁcation. In this paper, we generalize it

in this direction.

3 CATEGORY OF ATTRIBUTED

GRAPHS

To develop a categorical graph rewriting system we

must deﬁne a category (objects and morphisms) and

then explain how to apply a rule (in our case by the

computation of a pushout).

Let us recall that a pushout of two morphismsL

→

R, L

→ G is a couple of morphisms (G

′

→ H, R

′

→ H)

such that:

• i

′

◦ r = r

′

◦ i

• for every other couple of morphisms (R

→ H

′

→ H

′

) such that h ◦ r = g ◦ i it exists a unique

morphism c such that the diagram below com-

mutes:

′

As a consequence, the existence of pushout im-

plies the uniqueness of the object H up to isomor-

phism (cf. (Ehrig et al., 2006a), (L¨owe, 1993)). If we

have the two properties in the deﬁnition of pushout

but not the unicity of c, the construction is called a

weak pushout.

As in our previous work (Boisvert et al., 2011a),

the system T of λ-calculus is used to deﬁne attributes

and computation functions, but now we generalize

both the notion of an attribute and of a computation

function: instead of λ-terms in a ﬁxed context, full

typing judgements Γ ⊢ M : A with arbitrary context Γ

and partial typing proofs are considered. The result-

ing category of attributed graphs will be denoted by

. (For all notions that are not explained in the

main part of our paper please see Appendix.)

To have better idea of the power of T, let us recall

that it is a system of simply typed λ-calculus with sur-

jective pairing, terminal object and inductive types.

Type constructors include → for functional types, ×

for product(pairing) andInd for inductivetypes. Pair-

ing may be used to represent records, i.e., to “pack”

multiple attributes into one. The presenceof inductive

types permits to deﬁne all ordinary types of attributes,

like Bool, Nat, etc., as well as more complex types

like lists, binary trees, ω-trees, etc. Deﬁnition of in-

ductive types includes structural recursion over each

inductive type, this explains their particular interest in

modeling computations.

Below Θ is the set of all typing judgements of T.

Objects. Objects of Gr

are attributed graphs.

An attributed graph is deﬁned as 5-tuple G =<

,sr

,tg

,att

>, wherethe structural part (ﬁrst

4 items) consists of the set of vertices V

, the set of

edges E

and two functions source sr

: E

→ V

and

target tg : E

→ V

to connect edges to vertices. The

elements of the set V

∪ E

are called “elements of

the graph”. In this paper, we assume that V

∪ E

is fully ordered (lexicographically)

. The function

att

: V

∪ E

→ Θ associates exactly the judgement

Γ ⊢ M : A with each element of the graph.

To represent multiple attributes of a structural el-

ement, we use pairing to “pack” different data into

one λ-term. So each attribute can be seen as an n-

tuple containing all information attached to an ele-

ment. The n-tuple < M

,...,M

> is considered as an

abbreviation of the term < ... < M

>,...,M

Certain inductive type(s) can be reserved to rep-

resent labels in ordinary sense. E.g., let F

Ind(α){c

: α|...|c

: α} be a ﬁnite type. In T, we

have typing judgements Γ ⊢ c

: F

in any context Γ. If

we want to use c

in combination with other attribute

M : A, we may use < M, c

> of type A × F

. The

“absence of attributes” is represented by 0 : ⊤.

Morphisms. Let G,H be two attributed graphs. A

morphism f : G → H is deﬁned in three parts:

1. The “structural part” noted f

str

is a partial graph

homomorphism (Rozenberg,1997) from the stuc-

tural part of G to the structural part of H (cf. Fig.

2).For each v ∈V

∪E

, its pre-image (i.e. the set

of all its antecedents) is noted [v]

str

⊆ V

∪ E

2. The “attribute dependency relation” f

adr

is a rela-

In any case, it is close to ordinary practice when ver-

tices are represented by natural numbers.

MODELSWARD2013-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

tion between the sets V

∪ E

and V

∪ E

. For

each v ∈ V

∪ E

, its pre-image is noted [v]

adr

⊆

∪ E

. Applying to its elements att

, all at-

tributes of graph G which are used to compute v

can be obtained.

3. The “computational part” f

cmp

(v) is represented

by a partial proof. The partial proofs f

cmp

(v) have

to be “matched” with the attributes of G and H in

the following sense.

Let v ∈ V

∪ E

. Let att(v) = Γ ⊢ M : A. Let

[v]

adr

= {u

,...,u

},u

< ... < u

(as before, we

use the ordering on elements of G) and

att(u

) = Γ

⊢ M

: A

,...,att(u

) = Γ

⊢ M

: A

The partial proof tree p = f

cmp

(v) should have

exactly k active leaves with labels that are equal

to the attributes Γ

⊢ M

: A

,...,Γ

⊢ M

: A

(in

the order deﬁned by the order of the leaves of the

tree). The root of the tree should have a label that

is equal to the attribute att

(v). Parameter leaves

are not matched to anything. (See Fig. 2.)

Equality of Objects and Morphisms. For objects,

we use identity on structural part and βηι-equality of

judgements of T for attributes. For morphisms, f = g

requires the identity of f

str

and g

str

, f

adr

and g

adr

; for

computation functions, for all v the equality of f

cmp

and g

cmp

(v) w.r.t. βηι-equality is required (see deﬁ-

nition 6.5 of the Appendix

Categorical Structure on Gr

. The identity id

deﬁned using identity graph homomorphism as f

str

identity relation as f

adr

and canonical identity par-

tial proofs as f

cmp

(v). The composition of morphisms

(only the level of partial proof trees is non-trivial) is

deﬁned using composition of partial proof trees, deﬁ-

nition 6.6 of the Appendix.

Theorem 3.1. Gr

deﬁned above is a category.

Proof. Composition is associative due to associativ-

ity of the composition of graph homomorphisms, and

associativity of the composition of relations. For par-

tial proofs composition is associative too because of

conﬂuence and the fact that T is strongly normaliz-

able. Thus any evaluation strategy will terminate on a

same simply typed λ-term. It is easy to verify that for

every morphism f : G → H we have f ◦ Id

= f and

◦ f = f.

Remarks. This notion of equality is discussed in

detail in (Boisvert et al., 2011a). Here we would like

to remark that there is no reason to impose equiva-

lence relation on partial proofs themselves since the

We may obtain other interesting categorical structures

with different kinds of equality of judgements and partial

proofs, for example syntactic (graphical) equality of judge-

ments.

system we describe is intended to study the properties

of deductions, models etc. represented by attributed

graphs. So it is more natural to impose an equivalence

relation on attributes and attributed graphs as needed.

4 RULE APPLICATION BY A

WEAK PUSHOUT

COMPUTATION

As in the SPo approach, in our approach each mor-

phism r : L → R deﬁnes a transformation rule. The

auxilliary notion of an embedding is necessary to in-

dicate a “redex” - the part of the host graph to which

the rule can be applied.

Injective Attributed Graph Morphism. Let f :G →

H be an attributed graph morphism. f is injective if:

1. f

str

is an injective partial graph homomorphism

(i.e. ∀v

∈ V(G) ∪ E(G).( f

str

) = f

str

) ⇒

= v

));

2. f

adr

= f

str

;

3. for each v

′

∈ V(H) ∪ E(H):

• if [v

′

]

adr

is empty, then f

cmp

′

) is the partial

proof tree (cf. appendix) that has one node with

the label att(v

′

). It is at the same time its root

and its only leaf, which is not active.

• if [v

′

]

adr

is not empty (thus [v

′

]

adr

is a single-

ton because f

adr

is injective) then f

cmp

′

) is

canonical identity partial proof for the attribute

att(v

′

We shall call an embedding a total injective at-

tributed graph morphism.

Canonical Retraction of an Embedding. Let f :

G → H be an embedding. A retraction of f (or a left

inverse) is an attributed graph morphism f : H → G

such that f ◦ f = Id

With this deﬁnition, we have not necessarily f ◦

f = Id

, and f is not unique in general. That’s why

we give a canonical construction to obtain a retraction

of f. This construction is deﬁned by:

1. for every v

′

∈ V(H)∪E(H) if [v

′

]

str

is empty, i.e.,

′

does not belong to the image of f

str

, then v

′

does not belong to the domain of f

str

′

); if [v

′

]

str

is not empty then [v

′

]

str

= {v} for some v because

of injectivity and we pose f

str

′

) = v. Notice that

[v]

str

= {v

′

} by this deﬁnition.

2. f

adr

= f

str

3. for each v ∈ V(G) ∪ E(G) f

cmp

(v) is canonical

identity partial proof for the attribute att(v).

IncorporatingProofsinaCategoricalAttributedGraphTransformationSystemforSoftwareModellingandVerification

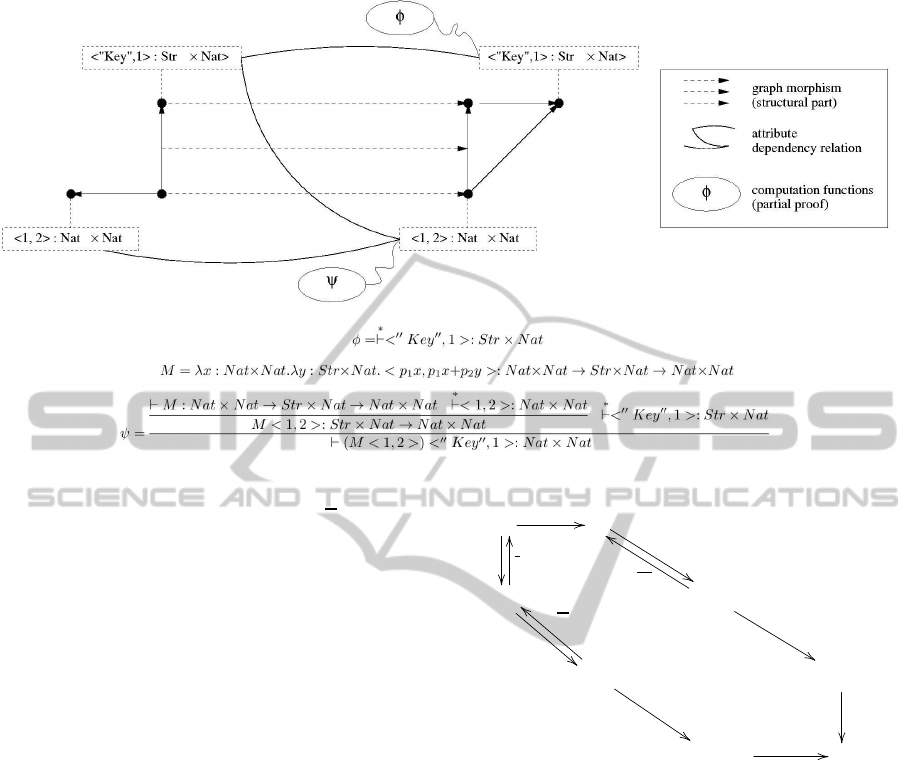
Figure 2: Attibuted graph morphism.

With this deﬁnition, it is easy to see that f ◦ f = Id

Construction of a Weak Pushout. The construction

of a (weak) pushout in case of application of a rule

is inspired by the paper by L¨owe and others (Rozen-

berg, 1997), but there will be differences due to our

deﬁnition of attributed graphs and graph morphisms.

The “starting point” is the pair of morphisms (L

→

R, L

→ G) where i is an embedding as deﬁnded above.

We want to compute the weak pushout (R

′

→ H, G

′

→

H) of this pair.

The ﬁrst step to deﬁne a pushout would be to

take the coproduct G + R of G and R (coproduct be-

ing here just the disjoint union). Next step would be

to factorize it by certain equivalence relation (creat-

ing (G+ R)

′

which contains equivalence classes), and

then to complete the construction using composition

with certain morphism p from factor object to pushout

object H.

We shall deﬁne each of the morphisms r

′

and i

′

a composition of three morphisms (Cf. ﬁgure 3) in

order to have

′

= G

′

→ (G+ R)

′

→ (G+ R)

′

→ H

and

′

= R

′′

→ (G+ R)

′′

→ (G+ R)

′

→ H

The objects and morphisms in these diagrams are

deﬁned in several steps.

• On the level of structure G+ R is disjoint union of

the graphs G and R;

′′

′

G+ R

′′

G+ R

′

(G+ R)

′

(G+ R)

′

Figure 3: Construction of weak pushout.

• on the level of attributes each element of G and R

in G+ R has the same attribute as in G and R;

• j

′

and j

′′

are inclusions respectively of G and R

into G + R, thus they are total injective attributed

graph morphisms.

To continue, we deﬁne ﬁrst the equivalence rela-

tion ∼

on the elements of the graph structure G+ R.

• let’s put a ∼

b for a,b ∈ G + R if ∃x ∈

L.( j

′

(i(x)) = a∧ j

′′

(r(x)) = b)

• then the relation ∼ is deﬁned as reﬂexive, sym-

metric and transitive closure of ∼

• notice that the elements of G+R which are not the

images of elements of G−i(dom(r)) form equiva-

lence classes consisting of single element (itself).

The elements of (G + R)

′

are deﬁned as equiva-

lence classes of elementsof G+R. It is easily checked

MODELSWARD2013-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

that this deﬁnition is consistent with the incidence re-

lation and the map sending each element of G + R

to its equivalence class is a (total) graph homomor-

phism. This map will be structural part of f

′

and f

′′

Moreover, each equivalence class with respect to

∼ containingan image of an elementof R may be seen

as a “span”, consisting of the image of this element

of R under j

′′

and the images of its antecedent via

r under j

′

◦ i. In particular, each equivalence class

contains exactly one image of an element of R. As a

consequence, the composition f

′′

str

◦ j

′′

str

is injective.

It permits also to deﬁne the attribute part of (G+

′

. Each equivalence class that contains an image

of an element of R has the same attribute as this ele-

ment has in R. Other equivalence classes (that have

the form { j

′

(y)},y ∈ G,y 6= i(x) for some x ∈ L) keep

the same attribute as in G.

The deﬁnitions of relational part and computation

functions of f

′

and f

′′

are different.

For f

′′

the relation f

′′

adr

connects the elements of R

with correspondingequivalence classes (it is bijective

on the R-part). There is no connections on the G-part.

The computation functions are identities.

Remark. The composition f

′′

◦ j

′′

is injective, in par-

ticular ( f

′′

◦ j

′′

)

str

is an injective total graph homo-

morphism,( f

′′

◦ j

′′

)

adr

= ( f

′′

◦ j

′′

)

str

and computation

functions are identities.

Now we may deﬁne f

′

as follows:

• ∀v ∈ img( j

′

◦ i):

′

= G + R

′

→ G

→ L

→ R

′′

→ G+ R

′′

→ (G+ R)

′

• for the elements of G−i(L), f

′

is like the identity.

As usual (cf. (Rozenberg,1997))H is deﬁned now

as for coequalizer construction. Let L

= dom(r). In

our case H will be a subgraph of (G+ R)

′

. The inci-

dence relation in (G + R)

′

is inherited from R and G.

The elements on H (on the level of graph structure)

are:

1. all the equivalence classes of the form

,...,x

,z} (x

,...,x

∈ j

′

(i(L

)),z ∈ j

′′

(r(L));

2. all the equivalence classes of the form {z}, z ∈

′′

(R− r(L));

3. all the equivalence classes of the form {x}, x ∈

′

(G − i(L)) that are not dangling edges (Rozen-

berg, 1997).

The attributes for the equivalence classes of the

ﬁrst two types are inherited from R and for the third

from G.

The morphism p is deﬁned as follows. Its struc-

tural part is identity on all elements of (G + R)

′

that

remain in H. We have also p

adr

= p

str

, and all com-

putation functions are identities.

Now i

′

, r

′

and H are deﬁned such that i

′

◦ r = r

′

◦ i.

Let h : R → H

′

and g : G → H

′

be two other mor-

phisms such that h ◦ r = g ◦ i. As i

′

is injective, we

can use the canonical retraction i

′

and take for c h ◦ i

′

and for elements who are not in the domain of i

′

extend c in order to make it in accord with g. The

commutativity on the level of computation functions

follows from the deﬁnition of equality of attributed

graph morphisms (cf section 3). Thus the diagram

commutes but in general the unicity of c is not guar-

anteed, so we have a weak pushout.

This is summarised in the following theorem.

Theorem 4.1. Let L

→ R be an attributed graph

morphism and L

→ G be an embedding in Gr

There exists weak pushout of L

→ R and L

→ G.

Moreover, it may be assumed that the morphism i

′

the (weak) pushout diagram is also an embedding.

Composite Rules. The proof of the theorem

above provides a canonical construction of the weak

pushout, in particular the vertical arrow i

′

is an em-

bedding like i. Such weak pushouts are sometimes

called speciﬁc weak pushouts because in the proof we

used the property that one of the two morphisms is an

embedding.

This construction of speciﬁc weak pushout per-

mits to compose the rules. Take two morphisms

→ R and R

′

→ R

′

. We have also their composition

′

◦r

−→ R

′

. The fact that i

′

in the speciﬁc weak pushout

above is also an embedding permits to construct the

second weak pushout representing an application of

the rule given by R

′

→ R

′

. It may be veriﬁed that the

construction of speciﬁc weak pushoutapplied directly

to r

′

◦ r gives the same graph H

′

after transformation.

Possible Generalizations: Schematic Morphisms

and Rule Schemas. The idea to use metavariables

in the deﬁnitions of graph transformation rules is sup-

ported by the practice of proof theory. Various ex-

amples are possible, e.g., one may deﬁne the disjoint

union of graphs using a rule schema (Boisvert et al.,

2011b). We shall use below only a restricted case of

rule schema based on the notion of schematic mor-

phism which we shall deﬁne precisely. For deﬁnitions

of partial proofs and schemas see Appendix, deﬁn-

tions 6.4 and 6.8.

Deﬁnition 4.1. A schematic morphism is obtained

if we replace partial proofs in the deﬁnition of mor-

phism in Gr

by partial proof schemas. An instance

of schematic morphism is any morphism in Gr

ob-

tained by instantiation of metavariables. Let r : L → R

be a schematic morphism. The rule schema in Gr

IncorporatingProofsinaCategoricalAttributedGraphTransformationSystemforSoftwareModellingandVerification

is the family of graph transformation rules deﬁned by

all instances of r : L → R.

5 EXAMPLES

To illustrate our transformation approach we present

in this section two detailed examples that may be of

interest from the point of view of model transforma-

tions. The ﬁrst one presents computationon attributes

representing inﬁnite trees. This can not be done us-

ing Σ-algebras. Possible applications include trans-

formations of inﬁnite models. The interest of dealing

with inﬁnite models is now taken into consideration

(Combemale et al., 2012). A model can be inﬁnite

according to the width or the depth of the graph. In

the example, we show how to deal with inﬁnite width

trees. Another example concerns coercive subtyp-

ing, that has important uses in software modeling and

reuse (Soloviev and Luo, 2001).

Let us mention also some examples not devel-

oped in this paper that can be easily treated using

our approach: (i) graph cloning, cf. (Boisvert et al.,

2011b); (ii) generation and transformation of proofs

in deductive systems, cf. (Boisvert et al., 2012) (e.g.,

Kleene-style premutations of rules (Kleene, 1952));

(iii) information transfer between attributes and struc-

ture; (iv) transformations of UML diagrams to rela-

tional models; (v) term graph rewriting (cf. (Baren-

dregt et al., 1997)).

5.1 UML Diagram to Database

Relational Model

Our approach permits to manage classical graph

transformation problems like UML diagram to

database relational model transformation. This prob-

lem is described in (). In (Taentzer et al., 2005) the

transformation using the the DPo approach ... In our

approach it is possible to manage this classical prob-

lem. In this paper we present only an example of

rule because it would take several pages to present

them all. The ﬁgure 4 presents the rule “Class2Table”

(Taentzer et al., 2005). As we use typed λ-calculus, it

necessary to deﬁne the types used in this example:

• the type Type is deﬁned as a ﬁnite type (see ap-

pendix 6) representing all “classes” of objects ma-

nipulated by the transformation:

Type = Ind(α){Class: α|Table : α|Column : α|...}

the constant Column and other constants are used in

other rules that are not described in this paper

• the type Connector is also deﬁned as a ﬁnite type

representing all temporary nodes that permit to

connect elements of the class diagram to elements

of the relational database model (see (Taentzer

et al., 2005)):

Connector = Ind(α){C2T : α|A2C : α|A2F : α|...}

• the type Name is the type describing the Name of

the classes or tables. It is more or less like String.

• the type Bool is used as the value of the attribute

is persistent of a node of Type Class.

We do not describe only one rule of this problem

here because it would take several pages to write them

all, and there is no complex attribute computation in

these rules. Thus our approach has no advantage on

other approach to manage this example. It is possi-

ble to deﬁne all the other rules presented in (Taentzer

et al., 2005) in the same way.

5.2 Managing Inﬁnity with Functional

Attributes

The use of λ-terms as attributes permits to manage

complex data structures that can represent inﬁnity.

As an example, the type T

which represents trees

with inﬁnite branching

can be deﬁned as follows:

= Indα{0 : α,

S : α → α,

L : (Nat → α) → α}

Using the standard recursion operators on in-

ductive types (see appendix), we can deﬁne com-

plex ω-trees and computations on these inﬁ-

nite tree structures. The ﬁgure 5 presents a

simple example of ω-tree deﬁned by the term

L(Rec

Nat→T

(0)(λx

Nat

λy

.S(y))). It is also possible

to deﬁne computations that transform these terms.

It is possible to write a function that takes as ar-

gument an inﬁnite tree, and give as results the trees

whith branches with pair numbers at every inﬁnite

branching:

Rec

→T

(0)(λx

.S)(λu.λv.(v◦ d))

5.3 Coercive Subtyping

The notion of coercion was introduced to represent

explicitly the transformation of the elements of the

In this example the attributes of a node have no “name”,

because they are stored in a tuple, and the position in the tu-

ple permits to identify the different attributes. We do like

this because we respect strictly on formalism, but in prin-

ciple it would be possible to add names for the different

elements of a tuple

nodes have an inﬁnite number of subtrees

MODELSWARD2013-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

Figure 4: Example of a rule.

... ...

Figure 5: Example of ω-tree deﬁned by the term

L(Rec

Nat→T

(0)(λx

Nat

λy

.S(y))). The length of the n-th

branch is n.

subtype into the elements of the supertype. It is com-

mon knowledge that the representation of the ele-

ments of a datatype is often changed when we pass

to a larger datatype, even if from mathematical point

of view it is merely an inclusion.

In coercive subtyping the subtyping relation A <

B is interpreted as existence of a certain deﬁnable

term c : A → B, with motivation of giving operational

semantics to calculi with subtyping and inheritance

(see, e.g., (Breazu-Tannen et al., 1991)).

In practice, certain “basic coercions” are deﬁned

and other coercions are derived using appropriate

rules. For example, to the transitivity of subtyping

relation corresponds composition of coercions, from

two subtyping relations A < B and C < D one can de-

rive B → C < A → D, respectively, from the coercions

: A → B and c

: C → D one may derive a coercion

c : (B → C) → (A → D).

In the calculus with inductive types basic coer-

cions are usually certain coercions between inductive

types, for example the type Bool = Ind(α){T : α|F :

α} is the subtype of Nat = Ind(α){0 : α|S : α → α}

(with coercion c(T) = S(0) : Nat, c(F) = 0 : Nat).

The set of coercions may be represented by an

acyclic attributed graph where attributes of the nodes

represent corresponding inductive types. To do that

we may use free variables, e.g., to represent the type

A we take the axiom x : A ⊢ x : A as the attribute. Two

nodes corresponding to the types A and B are con-

nected by an arc if the types are in subtyping relation,

and the attribute of this arc is the coercion ⊢ c : A → B

(coercion terms representing basic coercions have no

free variables).

The set of coercions is coherent if composition of

coercion terms along two paths with the same source

and target is equal. The graph is completed to transi-

tive closure (concerning the attributes, coherence per-

mits to do it without contradiction). Practical useful-

ness of this is clear, since the coercions “implement-

ing” the subtyping relation can be directly taken from

the graph.

One of the main results obtained in (Soloviev and

Luo, 2001) was that coherence of the set basic coer-

cions implies coherence of the set of all derived coer-

cions. The main consequence was that the subtyping

extension of the consistent type theory without sub-

typing remains consistent.

Here we shall consider as an example two graph-

rewriting rules (besides already mentioned transitiv-

ity) that may be used to extend already obtained co-

ercion graph. They include the following derivations

used to deﬁne new coercions.

d =

x : A

∗

⊢ x : A

x : A,z :C ⊢ x : A

x : A ⊢ λz : C.x :C → A

⊢ λx : A.λz : C.x : A → (C → A)

′

∗

⊢ c : A → B

z :C ⊢ c : A → B

f : C → A, z :C ⊢ c : A → B

f : C → A, z :C ⊢ f : C → A f : C → A,z :C ⊢ z : C

f : C → A, z :C ⊢ fz : A

f : C → A,z :C ⊢ c( f z) : B

f : C → A ⊢ λz : C.(c( fz)) : C → B

⊢ λ f : C → A.λz : C.(c( fz)) : (C → A) → (C → B)

Here in fact d is an ordinary derivation and d

′

is a

partial derivation, active leaves (we refer to Ap-

IncorporatingProofsinaCategoricalAttributedGraphTransformationSystemforSoftwareModellingandVerification

d’

[A] [B]

→ A] [C → B]

[A] [B]

[C → A] [C → B]

Figure 7: Rule 2.

x:A x:A

x:A x:A A→u:C A→u:C

λx:A λy:C.x:A → (C → A)

Figure 6: Rule 1.

pendix) are labeled by ∗. If A,B,C are considered

as the metavariables for arbitrary types and c as a

metavariable for arbitrary coercions, then we have

schemas of (partial) derivations instead of concrete

(partial) derivations. The instances will be obtained if

we take, e.g., Bool instead of A, Nat instead of B and

C, and concrete coercion c : Bool → Nat mentioned

above.

Of course, other rules to introduce new coercions

are possible, for example, a “contravariant” rule to

pass from A < B to B → C < A → C and the rules

for product types A∧ B.

Below we give an example of graph transforma-

tions using d and d

′

to deﬁne computation functions.

The rules are given in Fig. 6 and 7. In Fig. 7,

[A] denotes x : A ⊢ x : A, [B] denotes x

′

: B ⊢ x

′

: B

etc., c

denotes some coercion ⊢ c

: A → B, c

de-

notes ⊢ λx : A.λy : C.x : A → (C → A), c

denotes

λ.x

′

: B.λy

′

: C.x

′

: B → (C → B), and c

denotes

⊢ λf : C → A.λz : C.(c( fz)) : (C → A) → (C → B).

In Fig. 7 the left side may be assumed to be already

obtained by applications of the ﬁrst rule

6 CONCLUSIONS

The aim of this paper was to generalize our previously

deﬁned graph transformation system . As in (Boisvert

et al., 2011a), it is based on the SPo approach and its

main originality concerns the use of a partial deduc-

tions to express attribute computations. Type theory

The labels added using pairing may be used to avoid

repeated application of transformation rules to the same ar-

guments.

incorporates both λ-calculus and reductions as com-

putational mechanism, and has at the same time de-

duction rules for typing. The use of inductive types

permits to include user-deﬁned datatypes, as in many

modern programming languages, and recursion over

these types.

That gives to our approach a great expressive

power that permit to manage classical model transfor-

mations like UML to Relational databasemodel trans-

formation, and also more sophisticated examples like

computation on functions, on inﬁnite data structures,

or on proofs.

At the same time, thepresence of proofspermits to

establish connection between development and trans-

formation of software models and software certiﬁca-

tion and veriﬁcation.

Theoretically speaking, the SPo approach neces-

sitates the deﬁnition and the construction of a weak

pushout when dealing with attributes. A solution is

presented in this paper. In comparison with our pre-

vious papers, we presented a more powerful way to

describe transformation of attributes, using not only

computation with λ-terms but deduction rules.

The possible domains of applications include all

usual applications of graph transformations, e.g., ver-

iﬁcation and model transformations in software engi-

neering. Note that thanks to the approach described

above it is now possible to deal with certain inﬁnite

models. More “tight” relationship between computa-

tion, graph structure and proofs will permit also the

pursuit of much more speciﬁc goals, in particular in

the domain of computer-assisted reasoning and veri-

ﬁcation (Luo, 1994),(Soloviev and Luo, 2001).

As a principal example of deductive system based

on type theory we considered in this paper the sim-

ply typed λ-calculus with inductive types and pairing.

All the constructions, though, can be easily modiﬁed

to be used in case of higher order and dependent type

systems in proof assistants, as well as for purely logi-

cal systems and applications.

A former experiment (Tran et al., 2010) of imple-

mentation in Haskell language constitutes the basis

for building a sofware environment devoted to model

MODELSWARD2013-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

transformations using our new approach. This is a

natural practical extension of our current work.

REFERENCES

Baar, T., Strohmeier, A., Moreira, A. M. D., and Mellor,

S. J., editors (2004). UML 2004 - The Uniﬁed Mod-

elling Language: Modelling Languages and Applica-

tions. 7th International Conference, Lisbon, Portugal,

October 11-15, 2004. Proceedings, volume 3273 of

LNCS. Springer.

Barendregt, H., van Eekelen, M., Glauert, J., Kennaway, J.,

Plasmeijer, M., and Sleep, M. (1997). Term graph

rewriting. PARLE Parallel Architectures and Lan-

guages Europe, pages 141–158.

B´ezivin, J., Rumpe, B., Sch¨urr, A., and Tratt, L. (2005).

Model transformations in practice workshop. In MoD-

ELS Satellite Events, pages 120–127.

Boisvert, B., F´eraud, L., and Soloviev, S. (2011a). Typed

lambda-terms in categorical attributed graph rewrit-

ing. In 2nd WorKshop on Algebraic Methods in

Model-Based Software Engineering TOOLS 2011,

June 30th, 2011, Zurich, Switzerland . Electronic Pro-

ceedings in Theoretical Computer Science.

Boisvert, B., F´eraud, L., and Soloviev, S. (2011b). Typed

lambda-terms in categorical graph rewriting. In The

International Conference Polynomial Computer Alge-

bra, April 18-22, Saint-Petersburg, Russia, Euler In-

ternational Mathematical Institute.

Boisvert, B., F´eraud, L., and Soloviev, S. (2012). Graph

Transformations, Proofs, and Grammars. In Int. Conf.

Phylosophy, Mathematics, Linguistics, Aspects of In-

teraction, May 22-25, Saint-Petersburg, Russia, Euler

International Mathematical Institute.

Breazu-Tannen, V., Coquand, T., Gunter, C., and Scedrov,

A. (1991). Inheritance and implicit coercion. Infor-

mation and Computation, 93:172–221.

Bundy, A. (1988). The use of explicit plans to guide induc-

tive proofs. In Luck, E. and Overbeek, R., editors,

Proceedings of the 9th International Conference on

Automated Deduction (CADE), number 310 in LNCS,

pages 111–120. Springer, Argonne.

Chemouil, D. (2005). Isomorphisms of simple inductive

types through extensional rewriting. Math. Structures

in Computer Science, 15(5):875–917.

Combemale, B., Thirioux, X., and Baudry, B. (2012). For-

mally Deﬁning and Iterating Inﬁnite Models. In

France, R., Kazmeier, J., Atkinson, C., and Breu, R.,

editors, Proceedings of the 15th international con-

ference on Model driven engineering languages and

systems (MODELS’12), volume 7590 of LNCS, pages

119–133, Innsbruck, Austria. Springer.

Diestel, R. (2010). Graph Theory. Springer-Verlag, fourth

edition.

Ehrig, H. (1978). Introduction to the algebraic theory of

graph grammars (a survey). In Graph-Grammars and

Their Application to Computer Science and Biology,

pages 1–69.

Ehrig, H., Ehrig, K., Prange, U., and Taentzer, G. (2006a).

Fundamentals of Algebraic Graph Transformation

(Monographs in Theoretical Computer Science. An

EATCS Series). Springer-Verlag New York, Inc., Se-

caucus, NJ, USA.

Ehrig, H., Padberg, J., Prange, U., and Habel, A. (2006b).

Adhesive high-level replacement systems: A new cat-

egorical framework for graph transformation. Fun-

dam. Inf., 74(1):1–29.

Gentzen, G. (1934-35). Untersuchungen ¨uber das logische

Schliessen. In I, II, Math. Z. 39, pages 176–210, 405–

443.

Kleene, S. C. (1952). Permutability of inferences in

Gentzen’s calculi LK and LJ. Mem. Amer. Math. Soc.,

pages 1–26.

L¨owe, M., editor (1993). Algebraic approach to single

pushout graph transformation, TCS, volume 109.

Luo, Z. (1994). Computation and Reasoning: A Type The-

ory for Computer Science. International Series of

Monographs on Computer Science. Oxford University

Press, USA.

Luo, Z. (2008). Coercions in a polymorphic type system.

Math. Structures in Computer Science, 18(4):729–

751.

Orejas, F. (2011). Symbolic graphs for attributed graph con-

straints. J. Symb. Comput., 46:294–315.

Rebout, M. (2008). Une approche cat´egorique uniﬁ´ee pour

la r´ecriture de graphes attribu´es. PhD thesis, Univer-

sit´e Paul Sabatier, Toulouse, France.

Rebout, M., F´eraud, L., Marie-Magdeleine, L., and

Soloviev, S. (2011). Computations in Graph Rewrit-

ing: Inductive types and Pullbacks in DPO Approach.

In Szmuc, T., Szpyrka, M., and Zendulka, J., editors,

Advances in Software Engineering Techniques, CEE-

SET 2009, Krakow, Poland, October 2009, volume

7054 of LNCS, pages 150–163. Springer-Verlag.

Rebout, M., F´eraud, L., and Soloviev, S. (2008). A Uniﬁed

Categorical Approach for Attributed Graph Rewrit-

ing. In Hirsch, E. and Razborov, A., editors, Interna-

tional Computer Science Symposium in Russia (CSR

2008), Moscou 07/06/2008-12/06/2008, volume 5010

of LNCS, pages 398–410. Springer-Verlag.

Rozenberg, G., editor (1997). Handbook of Graph Gram-

mars and Computing by Graph Transformations, Vol-

ume 1: Foundations. World Scientiﬁc.

Soloviev, S. and Luo, Z. (2001). Coercion completion and

conservativity in coercive subtyping. Annals of Pure

and Applied Logic, 113–1:297–322.

Taentzer, G., Ehrig, K., Guerra, E., Lara, J. D., Leven-

dovszky, T., Prange, U., Varro, D., and et al. (2005).

Model transformations by graph transformations: A

comparative study. In Model Transformations in Prac-

tice Workshop at Models 2005, MONTEGO, page 5.

Tran, H. N., Percebois, C., Abou Dib, A., F´eraud, L., and

Soloviev, S. (2010). Attribute Computations in the

DPoPb Graph Transformation Engine (regular paper).

In GRABATS 2010, University of Twente, Enschede,

The Netherlands, 28/09/2010-28/09/2010, page (elec-

tronic medium), http://www.utwente.nl/en. University

of Twente.

IncorporatingProofsinaCategoricalAttributedGraphTransformationSystemforSoftwareModellingandVerification

APPENDIX

Typed λ-Calculus with Inductive Types

The system of λ-calculus in this paper is the simply

typed λ-calculus with surjective pairing, terminal

object and inductive types. For details see (Chemouil,

2005), here we recall the principal deﬁnitions con-

cerning this system that will be named T in the other

sections of this paper.

Deﬁnition 6.1. Types are either atomic types or de-

ﬁned by using a type constructor.

Atomic types are:

• the constant type ⊤;

• a ﬁnite or inﬁnite set S = {α,β,...} of type vari-

ables;

Type constructors are:

• → for functional types, which constructs A → B

for any types A and B

• × for product types, which constructs A × B for

any types A and B

• Ind, deﬁned as follows: let C be an inﬁnite set of

introduction operators ( constructors of elements

of inductive types), with C ∩ S = ∅. an inductive

type with n constructors c

, . .., c

∈ C , each of

them having the arity k

(with 1 ≤ i ≤ n), has the

form:

Ind(α){c

: A

→ ... → A

→ α;

... ;

: A

→ ... → A

→ α},

Here, every A ≡ A

→ ... → A

→ α is an induc-

tive schema, i.e., A

is:

– either a type not containing α;

– or a type of the form A

≡ C

→ ... → C

→ α,

where α does not appear in any C

ℓ∈1..m

(such

are called strictly positive operators).

Here Ind(α) binds the variable α.

Example 6.1. (Deﬁnition of types Bool, Nat and T

the type of ω-trees.)

= Ind(α){c

: α| ... |c

: α}

Bool = Ind(α){T : α|F : α}

Nat = Ind(α){0 : α| S : α → α}

= Ind(α){0

: α| S : α → α|L

: (Nat → α) → α}.

Deﬁnition 6.2. Let V be an inﬁnite set of variablesV

(with V ∩S ∩C = ∅). The set of λ-terms is generated

by the following grammar rules:

M ::= c|R

B,D

|x|(λx : B· M) | (M M) | < M M >

where x ∈ V , c ∈ C , B and D are arbitraty types, and

B,D

is the standard recursion operator (for details,

see (Luo, 1994), (Chemouil, 2005)).

All terms and types are considered up to α-

conversion, i.e., renaming of bound variables. Con-

text Γ is a set of term variables with types x

,...,x

: A

,...,x

distinct). Γ,∆ denotes the

union of contexts Γ,∆ (we assume that Γ, ∆ have no

common term variables). The expression Γ ⊢ M : A is

called typing judgement (or sequent). Its meaning is

“term M has type A in the context Γ”.

Deﬁnition 6.3. Here are the following typing axioms

and rules for the terms deﬁned above (A, B,D denote

arbitrary types, Γ arbitrary context).

Axioms.

• Γ,x : A ⊢ x : A, Γ ⊢ 0 : ⊤;

• For each inductive type C = Ind(α){c

|...|c

: A

} and 1 ≤ i ≤ n

Γ ⊢ c

: A

[B/α]

(for example, if C = Nat, we shall have Γ ⊢ 0 : Nat

and Γ ⊢ S : Nat → Nat);

• For C as above and any type D the axiom

Γ ⊢ R

C,D

:ϒ

,D) → ... → ϒ

,D) → C → D.

Typing Rules.

Γ ⊢ M : A Γ ⊢ N : B

Γ ⊢< M N >: A× B

(pair)

Γ ⊢ M : A× B

Γ ⊢ p

M : A

)

Γ ⊢ M : A× B

Γ ⊢ p

M : B

)

Γ,x : A ⊢ M : B

Γ ⊢ (λx : A · M) : A → B

(λ)

Γ ⊢ M : A → B Γ ⊢ N : A

Γ ⊢ (M N) : B

(app)

Remark 6.1. (i) The constant R

C,D

is called the re-

cursor from C to D. Notice that applying it (using

the rule app) to the terms M

: ϒ

,D),...,M

,D) we deﬁne the function R

C,D

...M

: C →

D. The following derived rule is often included:

Γ ⊢ M

: ϒ

,D)(1 ≤ i ≤ n)

Γ ⊢ (R

C,D

... M

) : C → D

(elim)

(ii) Usually the following structural rules are in-

cluded in T (they are admissible w.r.t. other rules):

Γ ⊢ M : B

Γ,x : A ⊢ M : B

(wkn)

Γ,x : A, x

′

: A ⊢ M : B

Γ,x : A ⊢ [x/x

′

]M : B

(contr)

(A,D) are certain auxilliary types used to deﬁne re-

cursion from C to D. They correspond to the types of func-

tions that appear in standard recursive equations overC. For

example, if C = D = Nat and A = Nat → Nat (the type of

successor S), then ϒ

Nat

(A,Nat) = Nat → Nat → Nat.

MODELSWARD2013-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

Γ ⊢ N : A Γ,x : A ⊢ M : B

Γ ⊢ [N/x]M : B

(subst)

Here [N/x] denotes substitution with renaming of

bound variables to avoid capture.

Normalization and Equality. The terms of the sys-

tem T are considered up to equality generated by

conversion relation. The α-conversion (renaming

of bound variables) was already mentioned. Other

conversions are

: (i) β-conversion (λx : A.M)N =

[N/x]M; (ii) η-conversion λx : A.(Mx) = M (where

x must not be free in M); (iii) and ι conversion for

recursion. The ι-conversion corresponds to one step

in recursive computation. It applies to the terms of

the form (R

C,D

...M

)(c

N), i.e. when the func-

tion deﬁned by recursion applied to the term begin-

ning by one of the introduction operators. For exam-

ple, for (R

Nat,Nat

ag)0 →

a and (R

Nat,Nat

ag)(Sn) →

Nat,Nat

ag)((gn)(Sn)) (here a : Nat is “initial value”

and g : Nat → Nat → Nat deﬁnes inductive step. The

exact general deﬁnition may be found in (Chemouil,

2005), p.884.

T is conﬂuent and strongly normalizing with re-

spect to βηι-reductions (directed conversions). De-

tailed description and normalization theorems for T

can be found in (Chemouil, 2005). Thus, the equiv-

alence relation on terms based on conversion (often

called βηι-equality) is decidable.

Proof Trees and Partial Proofs

An inference rule in proof theory is a couple

where

P is a list of premises, possible subject to some con-

straints. As examples one may take the rules of the

system T above. Usually in proof theory the presen-

tation of rules is schematic, that is, the metavariables

like Γ,∆ are used to represent arbitrary contexts, A,B

to represent arbitrary types etc. The presentation be-

low is generic, i.e., all the deﬁnitions can be modiﬁed

to accomodate a change of logical system, if only the

system has tree-form derivations build by application

of deduction rules to their premises.

Trees are a special case of graphs, and proof trees

are a special case of attributed graphs, but in any

case the trees below should be considered as part of

metatheory and not the objects of the category of at-

tributed graphs deﬁned in this paper. Applications

of trees to computations and data structures are usu-

ally straightforward, in difference from graphs in gen-

eral

. Our generalization of the deﬁnition of graph

We omit the contexts and types of terms.

The possibility to “embed” them into this category

seems obvious, but to our opinion it may be considered as

an invitation to study a hierarchy of graphs and attributes

transformation systems is based on the notion of par-

tial proof. Below the reader may assume that the par-

tial proofs are taken in the system T described above

but the deﬁnition will apply to any other deductive

system with appropriately deﬁned derivable objects.

According to standard deﬁnitions (cf. (Diestel,

2010)), a tree is a connected directed acyclic graph

J = (V,E) in which a single node is designated as root

and there is a unique path from the root to any other

node. If (x,y) ∈ V, we say that y is a child of x and y is

the parent of x. A leaf has no children. Since J has no

directed cycles, the transitive closure E

∗

of E deﬁnes

a partial strict order on V. There is a path from x to y

in J iff (x,y) ∈ E

∗

An ordered tree is the tree where outgoing edges

of any v ∈ V are numbered 0, 1,.... Thus, to any

(x,y) ∈ E

∗

corresponds a unique sequence of natu-

ral numbers. The lexicographic ordering of these se-

quences beginning at the root r permits to extend this

partial order to the unique linear order on V. In par-

ticular there is the natural ordering of the leaves.

The deﬁnitions below are modiﬁed deﬁnitions

from (Bundy, 1988) adapted to our case.

Deﬁnition 6.4. A partial proof is an ordered tree with

the following properties: (i) each node is labelled

with a sequent and the rule of inference which is ap-

plied to this sequent (backwards) to produce the (la-

bels of) the node’s children; (ii) the ﬁnal sequent (or

the goal) is the sequent at the root of the tree; (iii) for

the leaves, no rule of inference is speciﬁed; (iv) we

shall further distinguish “active” and “parameter”

leaves. Active leaves are marked by ∗.

Our purpose is to use partial proofs for attribute

transformations, and thus, the difference between ax-

ioms and other sequents is not relevant. In some cases

we may impose additional restrictions, e.g., that the

parameter leaves are axioms or that all leaves have

derivable sequents as labels.

The use of partial proofs instead of λ-terms to rep-

resent computation functions permits more ﬂexibility

concerning the choice of equality in the category of

graph transformations. The deﬁnitions and results be-

low will be valid for any equality (equivalence rela-

tion) on the set of sequents (logical formulas, judge-

ments). Usually (but not necessarily) the judgements

of the system T are considered up to βηι-equality.

Another choice may be syntactic (graphic) equality

of terms and types (with γ and Γ

′

equal as sets).

Next notion we are going to deﬁne is the equality

of partial proofs. In fact, the main requirement is that

the good properties of composition must be assured.

with alternating layers. The possibility seems interesting

but it is out of scope of this paper.

IncorporatingProofsinaCategoricalAttributedGraphTransformationSystemforSoftwareModellingandVerification

Deﬁnition 6.5. Partial proofs are equal if they have

the same number of active leaves, the labels of corre-

sponding active leaves (in order deﬁned by the trees)

and the labels of two roots are equal

The notion of composition of partial proofs is in-

spired by the notion of composition of multivariable

functions.

Deﬁnition 6.6. Let l

< ... < l

be all active leaves

(see deﬁnition above) of the partial proof P. Let P

,...,

be partial proofs and r

,...,r

their roots. Let

for all i, 1 ≤ i ≤ k the labels of l

and r

be equal.

The composition P ∗ (P

,...,P

) is obtained by iden-

tiﬁcation of each l

with its label and r

with its la-

bel (assuming other nodes disjoint). Order relations

are extended to the new tree in natural way. The ac-

tive leaves are now the union of the active leaves of

,...,P

and the root is the root of P.

The result is another partial proof. This composi-

tion is associative w.r.t. the equality deﬁned above.

Deﬁnition 6.7. The canonical identity partial proof

for the sequent (formula, judgement) S is the tree with

one node (which is the root and the one active leaf at

the same time) that has S as its label.

Schemas of Partial Proofs

It is common in proof theory to use axiom and rule

schemas instead of individual axioms and rules. In

the schemas the meta-variables may be used. The for-

mulations of axioms and rules of the system T above

are schematic. There may be metavariables of differ-

ent kinds, e.g., metavariables for terms, contexts, and

even for arbitrary variables as in the axiom schemas

or the rule (λ) above

Deﬁnition 6.8. (Partial Proof Schema.) A partial

proof schema is an ordered tree with the following

properties: (i) each node is labelled with a meta-level

sequent. (ii) each node except the leaves is labeled

also with the rule of inference which is applied to this

sequent (backwards) to produce the node’s children

(and the children of course must be the meta-level se-

quents matching the premises of this rule). (iii) the

ﬁnal meta-level sequent (or the goal) is the meta-level

sequent at the root of the tree, some of the leaves are

marked as active by ∗.

An alternative deﬁnition would be to require the equal-

ity of the whole ordered trees and all corresponding labels.

Essentially, this practice is similar to the use of non-

terminals in the formal grammars.

MODELSWARD2013-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment