Image Pyramids as a New Approach for the

Determination of Fractal Dimensions

Michael Mayrhofer-Reinhartshuber, Philipp Kainz and Helmut Ahammer

Institute of Biophysics, Medical University of Graz, Harrachgasse 21/IV, A-8010 Graz, Austria

Keywords:

Fractals, Pyramid Dimension, Fractal Dimension, Image Analysis.

Abstract:

The consideration of different scales and the application of fractal methods on digital images is of high im-

portance if real world objects are investigated. In this context the fractal dimension is an important parameter

to characterize structures and patterns. An accurate understanding of them is obligatory if signiﬁcant and

comparable results should be obtained. Recently a new method using an image pyramid approach was com-

pared to the very popular Box Counting Method. The intriguing results showed that a trustable value for the

fractal dimension could be obtained in much faster computational times compared to traditional Box Counting

algorithms. In addition to these results of this new approach, which is only applicable to binary (black/white)

images, we present developments toward the application to grey value/color images. Especially the determina-

tion of the grey value surface and the interpolation used to downscale the images seem to have major inﬂuence

on the results achieved.

1 INTRODUCTION

The development of both image analysis and the

available image processing techniques results in an in-

creasing number of parameters, that can be extracted

from investigated images. But discrepancies occurred

in the results of different research groups which were

studying images of the same object at different res-

olutions, especially if these objects were of natural

origin.

In 1981 Paumgartner et al. (Paumgartner et al.,

1981) showed in a pioneering study that the results

obtained from image analysis of subcellular mem-

brane systems seemed to depend on the resolution

scale used. Their estimations for the surface density

of inner mitochondrial membranes and endoplasmic

reticulum increased signiﬁcantly as the magniﬁcation

of their images was increased. This behavior was ex-

plained with a resolution effect, using a concept pro-

posed by Mandelbrot (Mandelbrot, 1977): the con-

cept of fractals.

If properties of these objects called fractals are in-

vestigated, similar patterns and structures are gained

at different scales because ﬁner and ﬁner shapes are

revealed every time the resolution is increased. To-

gether with a non-integer value for the dimension this

is one of the main characteristics of fractals. The con-

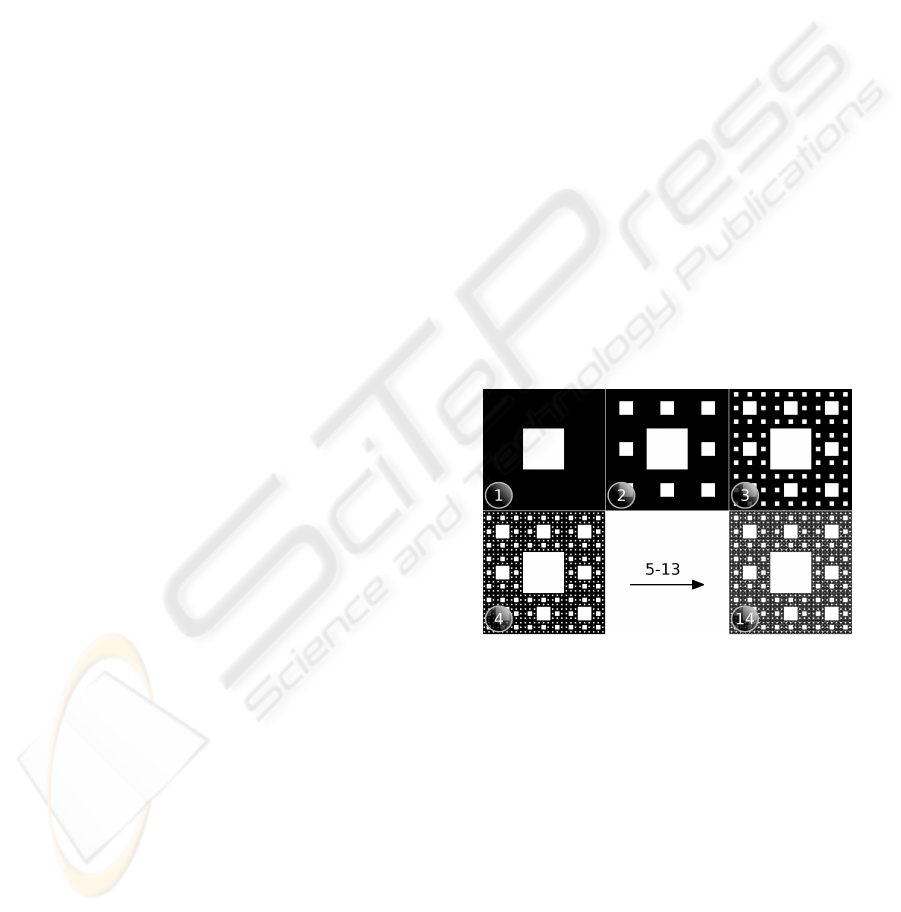
cept of fractals is illustrated in Figure 1, where suc-

Figure 1: Image set of a fractal (”Sierpinski Carpet”). In

every iterative construction step (in this example up to 14)

the fractal dimension is increased.

cessive steps of the construction process of an image

with fractal dimension are shown. In his most popu-

lar publication titled The Fractal Geometry of Nature,

Mandelbrot (Mandelbrot, 1983) showed that a lot of

objects of natural origin have fractal characteristics.

The consideration of differentscales and the appli-

cation of fractal methods on these types of structures

is not just possible, it is obligatory if signiﬁcant and

comparable results should be obtained. Conventional

morphology based on a single scale measurement al-

ways implies a Euclidean geometry as its basis. In

most studies dealing with images taken in a medical

context a concept based on non-fractal geometry can-

239

Mayrhofer-Reinhartshuber M., Kainz P. and Ahammer H. (2013).

Image Pyramids as a New Approach for the Determination of Fractal Dimensions.

In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 239-243

DOI: 10.5220/0004325902390243

 SciTePress

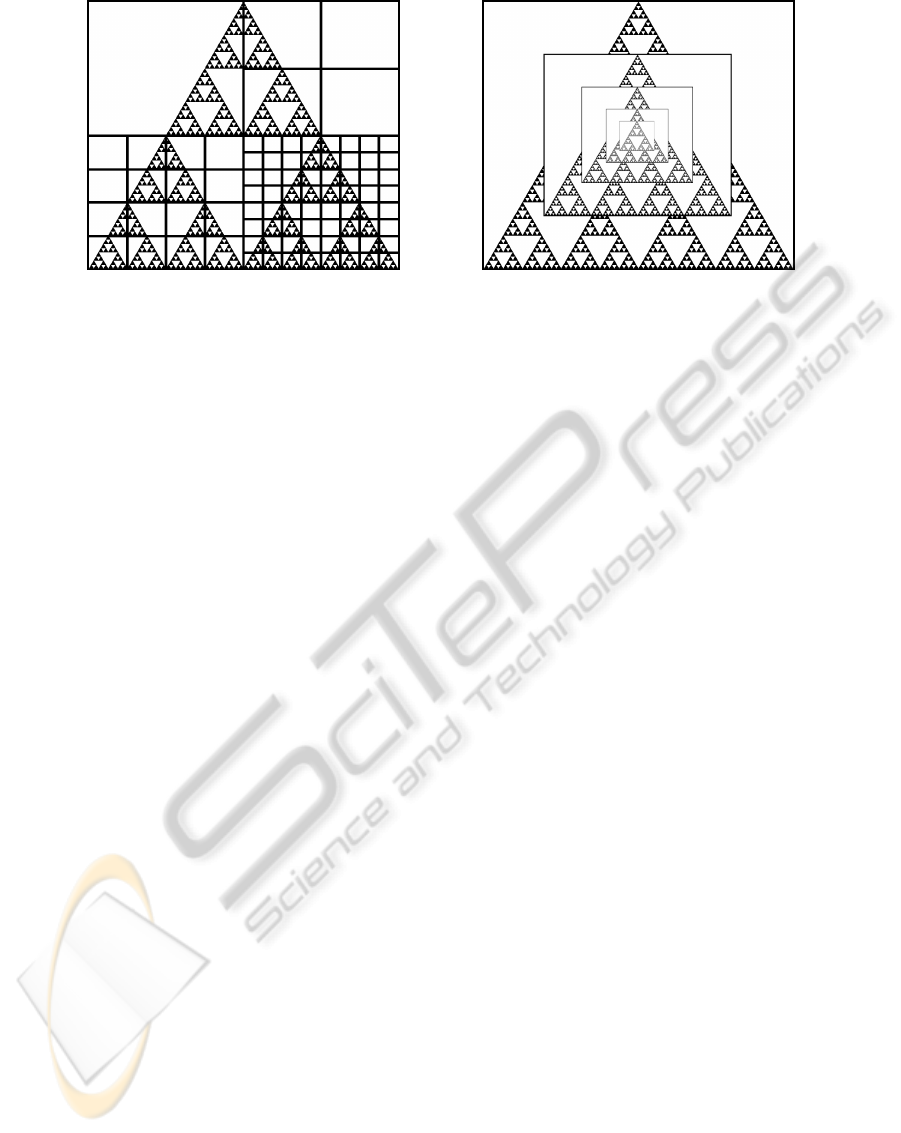
(a) (b)

Figure 2: (a) Principle of Box Counting Method applied to a standard fractal (”Sierpinsky Gasket”) showing different iteration

steps (box sizes) of the method in every quarter of the image. (b) Principle of Pyramid Method showing different iteration

steps (image sizes).

not yield comparable results, as for example Losa et

al. (Losa et al., 2011) stated in their discussion of a

publication concerning pyramidal cells in the rat so-

matosensory cortex (Romand et al., 2011). The im-

portance of scaling laws and network structures for

the understanding of processes of health and disease

in medical research was outlined by West very re-

cently (West, 2012).

However, the application of fractal methods im-

poses certain requirements on the images under in-

vestigation. A sufﬁcient resolution when calculating

fractal properties as well as inﬂuences of edge detec-

tion algorithms were determined and discussed by our

group some years ago (Ahammer et al., 2003; Aham-

mer and DeVaney, 2004). On the one hand images

with higher and higher resolutions improve the gain-

able output of image analysis. On the other hand

large amounts of data have to be handled by the im-

plemented methods. Therefore, it can be stated that

there is a demand for new approaches and methods in

fractal analysis which are able to handle images with

a high number of pixels in acceptable computational

times.

2 METHODS

2.1 Box Counting Methods and Grey

Value Surfaces

Based on the concepts of the Hausdorff deﬁnition of

a dimension, the Box Counting Method (BCM, illus-

trated in Figure 2(a)) was deﬁned by Russell et al. and

is the most popular algorithm in contemporary fractal

analyses (Hausdorff, 1918; Mandelbrot, 1983; Rus-

sell et al., 1980; Lopes and Betrouni, 2009).

The mathematical foundations and characteristics of

the BCM are well investigated and its limitations

(binarization, strictly valid only for statistically self-

similar sets, box size sensitivity) are known (Keller

et al., 1989; Normant and Tricot, 1991; Appleby,

1996; Pruess, 1995).

The approach for handling grey value images

is called the Differential Box Counting Method

(DBCM) and was proposed by Chaudhuri and Sarkar

(Sarkar and Chaudhuri, 1992; Sarkar and Chaudhuri,

1995; Chaudhuri and Sarkar, 1995). Its development

and improvements later on made it possible to over-

come some of the limitations constraining the stan-

dard BCM (Jin et al., 1995; Biswas et al., 1998).

The BCM can easily be implemented and it is

used throughout scientiﬁc communities dealing for

example with images or signals originating in diverse

medical investigations (e.g. photographs, histological

images, optical coherence tomography, ...) (Higgs,

2011; Jelinek et al., 2011; Sullivan et al., 2011). Nev-

ertheless, there exist several disadvantages of the Box

Counting Methods, e.g. the high computational time

needed for evaluating the fractal dimension of im-

ages with high pixel count. Furthermore, Box Count-

ing Methods have limitations regarding the choice of

the box sizes. As pointed out by Pickover and Kho-

rasani there were studies to ﬁnd upper and lower lim-

its for the box sizes and it was shown that the Box

Counting Methods underestimate the true values of

the fractal dimensions. Disturbance by noise which

also leads to lower fractal dimension values was in-

vestigated (Pickover and Khorasani, 1986; Bisoi and

Mishra, 2001; Asvestas et al., 1998; Lee and Hsieh,

2010).

2.2 Pyramid Method

Recently the determination of the fractal dimension

using a new method was developed by our group

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

240

(a) (b)

Figure 3: Calculated fractal dimensions of the Sierpinski Gasket ((a), 8192 x 8192 pixels, 1-14 iteration steps). (b) Values

of the Pyramid Method (linear interpolation). (c) Values of the Pyramid Method (cubic interpolation). (d) Values of the Box

Counting Method.

(Ahammer and Mayrhofer-R., 2012). The major con-

clusions of the analysis of the new method were that

the obtained values for the fractal dimensions of bi-

nary images have the same quality as when deter-

mined with the BCM but within signiﬁcantly shorter

computational times. So far the method was only de-

veloped for binary (black/white) images.

The approach of the method is the origin of

the introduced names Pyramid Method (PM) for the

method itself and Pyramid Dimension for the fractal

dimension value obtained, respectively. It uses image

pyramids which are in fact sequences of identical im-

ages but at different sizes. The original image having

the biggest size represents the bottom of the pyramid.

The size of this bottom image is then reduced succes-

sively (using a suitable interpolation algorithm) until

it is no more than one pixel, which can be thought

of as the top of the pyramid (see Figure 2(b) for an

illustration). For each image size the number N of

object pixels is counted, with N

as the number of

object pixels in the original image. A value for the

pyramid dimension is obtained by applying the men-

tioned standard technique of fractal analysis. From

the double logarithmic plot of N/N

versus the scal-

ing variable used to scale down the images a slope can

be extracted representing the value for the fractal di-

mension of the digital images.

The results obtained are quite identical to the data

gained from using the BCM. Calculated values for the

fractal dimensions of 14 subsequent images of a Sier-

pinski Gasket (Figure 3 (a)) are shown in Figure 3

(b)-(d). Results obtained by the Pyramid Method with

linear interpolation for downscaling were equal to re-

sults obtained by the Box Counting Method. Differ-

ences to the results obtained by the Pyramid Method

using cubic convolution interpolation were below one

per mill and therefore negligible. Advantages of the

PM over other comparable methods are its simple im-

plementation and a signiﬁcant reduction of calcula-

tion time. PM was shown to be approximately ten

times faster than BCM. Nevertheless, it should be

mentioned that the interpolation method used when

downscaling the images affects the result of the cal-

culation. With binary images linear and cubic convo-

lution interpolation algorithms result in trustable re-

sults whereas nearest neighbor resampling should be

avoided. Also resampling without interpolation does

not yield acceptable results. Concluding it can be

stated that for binary images PM is superior to BCM

(Ahammer and Mayrhofer-R., 2012).

As the next step toward the applicability of the

PM to high resolution images of various sources it

has to be able to handle grey value images. For that

purpose the two-dimensional grey value images are

transformed to surfaces in three-dimensional space

using the grey value as a third coordinate. The area

ImagePyramidsasaNewApproachfortheDeterminationofFractalDimensions

241

of these surfaces should be a usable parameter for

determining a value for the fractal dimension. The

ﬁnding of an accurate and fast method for the cal-

culation of these grey value surface areas is of high

importance. So far, two known methods are already

implemented: one method based on gradient analy-

sis (Chinga et al., 2007) and another one known as

Blanket Method (or Minkowski Dilation Method for

surfaces) (Peleg et al., 1984; Tang et al., 2002). At

the moment test results are evaluated. Further meth-

ods as the Isarithm Method (Shelberg et al., 1983)

or the Triangular Prism Method (Clarke, 1986) and

its improvements (Sun, 2006) will be tested. Also

the signiﬁcance of the gained parameters is expected

to be highly inﬂuenced by the interpolation methods

used when rescaling the images. Therefore, a detailed

evaluation of different existing methods, an improve-

ment of them together with a development of own al-

gorithms both for the surface area calculation and for

the interpolation are important tasks to tackle. The

results of the developed method have to be compared

to the results obtained by the well established Box

Counting or other trustable methods. Especially sig-

niﬁcant improvements in computational time are ex-

pected as indicated by experiences with the Pyramid

Method applied to binary images. This is of high im-

portance considering the fact that the image size is ex-

pected to increase in the future, for instance because

of steadily improvingscanning devices, such as whole

slide imaging.

3 CONCLUSIONS

The binary Pyramid Method applied with speciﬁc

(linear and cubic convolution) interpolation methods

yields results similar or at least comparable with re-

sults obtained from the popularBox Counting Method

(Ahammer and Mayrhofer-R., 2012). Based on these

results it is expected that an extension to grey value

images, which is in development and evaluation at

the moment, results in a reliable and fast method for

determining fractal properties of structures in digi-

tal images. By applying the new Pyramid Method

the analysis of grey value images having a high pixel

count should be feasible in signiﬁcantly faster com-

putational times than compared to methods used pre-

viously by the scientiﬁc community.

REFERENCES

Ahammer, H. and DeVaney, T. T. J. (2004). The inﬂuence

of edge detection algorithms on the estimation of the

fractal dimension of binary digital images. Chaos,

14(1):183–188.

Ahammer, H., DeVaney, T. T. J., and Tritthart, H. A. (2003).

How much resolution is enough? Inﬂuence of down-

scaling the pixel resolution of digital images on the

generalised dimensions. Physica D, 181:147–156.

Ahammer, H. and Mayrhofer-R., M. (2012). Image pyra-

mids for calculation of the box counting dimension.

Fractals, 20:281.

Appleby, S. (1996). Multifractal characterization of the dis-

tribution pattern of the human population. Geograph-

ical Analysis, 28(2):147–160.

Asvestas, P., Matsopoulos, G. K., and Nikita, K. S. (1998).

A power differentiation method of fractal dimension

estimation for 2-d signals. Journal of Visual Commu-

nication and Image Representation, 9:392–400.

Bisoi, A. K. and Mishra, J. (2001). On calculation of frac-

tal dimension of images. Pattern Recognition Letters,

22:631–637.

Biswas, M. K., Ghose, T., Guha, S., and Biswas, P. K.

(1998). Fractal dimension estimation for texture im-

ages: A parallel approach. Pattern Recognition Let-

ters, 19:309–313.

Chaudhuri, B. B. and Sarkar, N. (1995). Texture segmen-

tation using fractal dimension. IEEE Transactions on

Pattern Analysis and Machine Intelligence, 17:72–77.

Chinga, G., Johnsen, P. O., Dougherty, R., Berli, E. L., and

Walter, J. (2007). Quantiﬁcation of the 3d microstruc-

ture of sc surfaces. J Microsc, 227(Pt 3):254–265.

Clarke, K. C. (1986). Computation of the fractal dimension

of topographic surfaces using the triangular prism sur-

face area method. Computers & Geosciences, 12:713–

722.

Hausdorff, F. (1918). Dimension und ¨außeres Maß. Mathe-

matische Annalen, 79(1-2):157–179.

Higgs, R. (2011). Imaging: Fractal analysis for chd mortal-

ity. Nature Reviews Cardiology, 8(2):62.

Jelinek, H. F., Ristanovic, D., and Milosevic, N. T. (2011).

The morphology and classiﬁcation of alpha ganglion

cells in the rat retinae: a fractal analysis study. J Neu-

rosci Methods, 201(1):281–287.

Jin, X. C., Ong, S. H., and Jayasooriah (1995). A practi-

cal method for estimating fractal dimension. Pattern

Recognition Letters, 16:457–464.

Keller, J. M., Chen, S., and Crownover, R. M. (1989). Tex-

ture description and segmentation through fractal ge-

ometry. Computer Vision, Graphics, and Image Pro-

cessing, 45:150–166.

Lee, W.-L. and Hsieh, K.-S. (2010). A robust algorithm for

the fractal dimension of images and its applications to

the classiﬁcation of natural images and ultrasonic liver

images. Signal Processing, 90:1894–1904.

Lopes, R. and Betrouni, N. (2009). Fractal and multifractal

analysis: A review. Medical Image Analysis, 13:634–

649.

Losa, G. A., Ieva, A. D., Grizzi, F., and Vico, G. D. (2011).

On the fractal nature of nervous cell system. Frontiers

in Neuroanatomy, 5.

Mandelbrot, B. B. (1977). Fractals: Form, Chance and

Dimension. W. H. Freeman & Company, 1st edition.

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

242

Mandelbrot, B. B. (1983). The Fractal Geometry of Nature :

Updated and Augmented. W. H. Freeman & Company,

New York.

Normant, F. m. c. and Tricot, C. (1991). Method for eval-

uating the fractal dimension of curves using convex

hulls. Phys. Rev. A, 43:6518–6525.

Paumgartner, D., Losa, G., and Weibel, E. R. (1981). Reso-

lution effect on the stereological estimation of surface

and volume and its interpretation in terms of fractal

dimensions. J Microsc, 121(Pt 1):51–63.

Peleg, S., Naor, J., Hartley, R., and Avnir, D. (1984). Multi-

ple resolution texture analysis and classiﬁcation. IEEE

Transactions on Pattern Analysis and Machine Intel-

ligence, PAMI-6(4):518–523.

Pickover, C. A. and Khorasani, A. (1986). Fractal charac-

terization of speech waveform graphs. Computers &

Graphics, 10(1):51–61.

Pruess, S. A. (1995). Fractals in the Earth Sciences, chapter

Some remarks on the numerical estimation of fractal

dimension, pages 65–75. Plenum Press.

Romand, S., Wang, Y., Toledo-Rodriguez, M., and

Markram, H. (2011). Morphological development

of thick-tufted layer v pyramidal cells in the rat so-

matosensory cortex. Frontiers in Neuroanatomy, 5.

Russell, D. A., Hanson, J. D., and Ott, E. (1980). Dimen-

sion of strange attractors. Physical Review Letters,

45:1175–1178.

Sarkar, N. and Chaudhuri, B. B. (1992). An efﬁcient ap-

proach to estimate fractal dimension of textural im-

ages. Pattern Recognition, 25:1035–1041.

Sarkar, N. and Chaudhuri, B. B. (1995). Multifractal and

generalized dimensions of gray-tone digital images.

Signal Processing, 42:181–190.

Shelberg, M., Lam, N., and Moellering, H. (1983). Mea-

suring the fractal dimension of surfaces. Proceedings

of the Sixth International Symposium on Computer-

Assisted Cartography, 6:319–328.

Sullivan, A. C., Hunt, J. P., and Oldenburg, A. L. (2011).

Fractal analysis for classiﬁcation of breast carcinoma

in optical coherence tomography. J Biomed Opt,

16(6):066010.

Sun, W. (2006). Three new implementations of the trian-

gular prism method for computing the fractal dimen-

sion of remote sensing images. Photogrammetric En-

gineering & Remote Sensing, 72(4):373–382.

Tang, Y. Y., Tao, Y., and Lam, E. C. M. (2002). New method

for feature extraction based on fractal behavior. Pat-

tern Recognition, 35:1071–1081.

West, G. B. (2012). The importance of quantitative systemic

thinking in medicine. Lancet, 379(9825):1551–1559.

ImagePyramidsasaNewApproachfortheDeterminationofFractalDimensions

243