Can Software Transactional Memory Make

Concurrent Programs Simple and Safe?

Ketil Malde

Institute of Marine Research, Bergen, Norway

Keywords:

Software Transactional Memory, Genome Assembly.

Abstract:

Parallel programs are key to exploiting the performance of modern computers, but traditional facilities for

synchronizing threads of execution are notoriously difﬁcult to use correctly, especially for problems with

a non-trivial structure. Software transactional memory is a different approach to managing the complexity

of interacting threads. By eliminating locking, many of the complexities of concurrency is eliminated, and

the resulting programs are composable, and thus simpliﬁes refactoring and other modiﬁcations. Here, we

investigate STM in the context of genome assembly, and demonstrate that a program using STM is able to

successfully parallelize the genome scaffolding process with a near linear speedup.

1 INTRODUCTION

As multi-core processors are becoming common-

place, parallel programs are crucial for performance

critical computation. Many problems can easily be

partitioned into subproblems that can be solved inde-

pendently (so-called “embarrassingly parallel” prob-

lems) but other problems are inherently more com-

plicated, and are best solved by multiple interacting

threads. In this case, care must be taken to keep sepa-

rate threads of execution from interacting in ways that

cause the program to behave incorrectly.

Traditionally, the shared data in parallel programs

is protected by synchronization primitives (locks) that

prevent simultaneous access to data structures. How-

ever, it is still quite difﬁcult to write correct programs

using these primitives, and incorrect or careless usage

cause well-known problems like deadlocks and race

conditions (Lee, 2006). In addition, independent pro-

gram parts that use locking primitives are in general

not composable, and for instance, refactoring a pre-

viously correct program can introduce new synchro-

nization problems (Harris et al., 2005).

Software transactional memory (Shavit and

Touitou, 1995), or STM, represents a different ap-

proach. Here, state that is shared between threads

is accessed in transactions, and the state is stored in

transactional variables. If multiple threads run simul-

taneous transactions that attempt to modify the same

state, only one of the transactions succeeds, the others

are rolled back and will be rescheduled by the run-

time system.

Since there is no explicit locking, deadlocks are

eliminated, and transactions are either committed

completely or not at all, so intermediate (and possibly

inconsistent) state is never exposed. In addition, STM

transactions are composable (Harris et al., 2005). The

disadvantage is a potentially higher overhead, both

because transactions need to log access to transac-

tional variables, and because transactions sometimes

need to be restarted from scratch, which duplicates

work.

Here, we investigate how STM can be applied to

the problem of genome scaffolding, the process where

the components of a partially assembled genome se-

quence are ordered and oriented to provide a more co-

herent (but often discontiguous) whole. A scaffolder

program is implemented in Haskell using STM, and

achieves a near linear speedup with the number of

processors.

1.1 Software Transactional Memory in

Haskell

There exist implementations of software transactional

memory for many programming languages (e.g.,

Brevnov et al., 2008; Ni et al., 2008). Some of the

problems faced by implementers is that the encapsu-

lation of transactions is not easily enforced, and ex-

ceptions, I/O operations and global, mutable state can

break the transaction abstraction. Harris et al. (2005)

223

Malde K..

Can Software Transactional Memory Make Concurrent Programs Simple and Safe?.

DOI: 10.5220/0004326702230228

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2013), pages 223-228

ISBN: 978-989-8565-35-8

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

discuss this in more detail.

One distinguishing feature that sets Haskell apart

from the majority of programming languages, is that

it is pure: the result of a function depends only on

its parameters, and the return value may not depend

on or affect external state, read or write ﬁles, or

have other external effects. However, many effect-

ful computations can be simulated in pure code (e.g.

state can be passed between functions as a parame-

ter), and Haskell uses a structure (or pattern) called a

monad for convenient manipulation of effectful com-

putations. In essence, a monad allows the creation of

an environment where speciﬁc effects are made avail-

able. This can also include non-pure effects, and, un-

surprisingly, I/O operations are only available in the

appropriate monad.

The type system distinguishes effectful computa-

tions from pure computations, and enforces that pure

computations never can execute impure operations.

For instance, I/O operations are guaranteed to only

be executed in the context of the IO monad. A monad

is a parametric type, so for some type

, the type

designates an I/O action which can be executed to

produce a value of type

. For instance,

getChar

has

type

IO Char

, as it is an I/O action that can produce

a character. Apart from the ability to be executed by

the run-time system,

getChar

is a normal value, and

like other values it can be assigned to variables and

manipulated with functions. Using combining func-

tions, larger programs can be built that interact with

their environment in complex ways.

In Haskell, STM is implemented as a monad, and

transactions are conﬁned to this environment. Sim-

ilar to the IO example, a type

STM a

designates a

transaction that, when executed, returns a value of

some type

. In the STM monad, mutable data struc-

tures are available as explicitly declared transactional

variables, or

TVar

s. Using the same mechanism and

syntax as other monads, simple transactions can be

composed into more complex ones. Transactions can

be executed in the IO monad, using the

atomically

function, which converts a value of type

STM a

to a

value of type

IO a

It is important to note that

TVar

s are only ac-

cessible from the STM monad. This makes them

unavailable to non-transactional computations (i.e.,

plain functions), and the static type system rigidly en-

forces this encapsulation. Similarly, transactions have

no means to modify other state, in particular, they are

prevented from performing I/O operations or mod-

ifying global variables. This separation makes the

While most monads can be – and usually are – imple-

mented as simple libraries, the IO monad is special, and

executed by the run-time system.

Haskell STM implementation safer to use, and may

explain why STM implementationsin other languages

with less rigid type systems have been less successful.

1.2 Genome Assembly and Scaffolding

The sequencing process usually produces a large set

of short fragments (or reads) from random positions

in the genome. Given such a set of reads, the genome

assembly problem is to reconstruct the originating

genome sequence. The traditional approach is the

method called overlap–layout–consensus (Bonﬁeld

et al., 1995; Myers et al., 2000), or OLC:

1. Identify overlaps by aligning each sequence

against all others

2. Determine the layout – order and orientation – of

the reads that is best supported by the alignments

3. Merge sequences according to layout to produce a

single contiguous consensus sequence

The ﬁrst step is trivially parallelizable (each read

is independent of the others, and can be independently

aligned), but the second step is more complicated.

Usually, the problem is modeled as a graph where

each read is a node, and there exists an edge between

nodes if the corresponding reads are determined to

overlap. Assembly is then equivalent to identifying

a Hamiltonian path in the graph, which is an NP-

complete problem.

The layout phase processes the overlap graph to

produce a linear progression of the reads, and al-

though distant parts of the graph can be processed

independently, care must here be taken if two oper-

ations attempt to modify the same nodes simultane-

ously. The implementation details of assemblers are

not often published, but observation of some com-

mon OLC assemblers indicates that they commonly

perform alignments in parallel, but later run the lay-

out phase using a single thread of execution.

This

supports the view that constructing a correct locking

scheme for doing graph updates in parallel is difﬁ-

cult. In addition, it would probably be inefﬁcient,

as it would incur locking overhead also for the non-

colliding updates - likely to be the vast majority of

them.

A popular alternative to OLC is the de Bruijn assem-

bly (Pevzner et al., 2001). This is less resource-intensive,

as it avoids the all-against alignment phase, and it is equiv-

alent to identifying an Eulerian path. But it is also easier

to parallelize in practice, which may also be a factor that

contributes to its popularity.

E.g. Newbler only parallelizes computing alignments

and generating output. (454 Life Sciences Corp., 2010)

BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

224

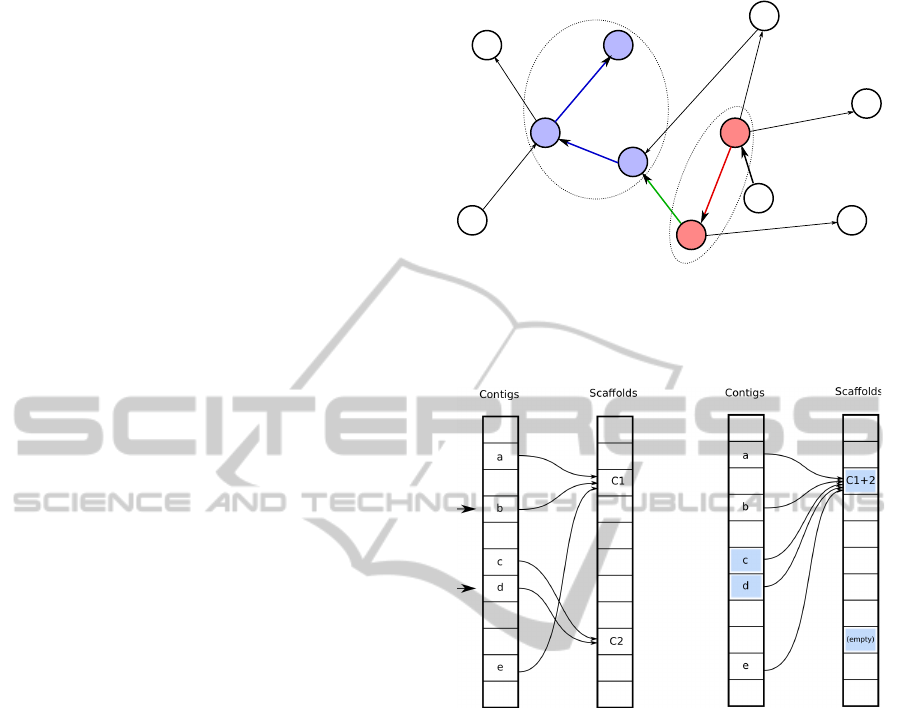
Genome scaffolding is closely related to assem-

bly. Here, the assumption is that a genome has been

sequenced and assembled into a set of contigs. In

addition to overlaps, there exists external informa-

tion about the orientation and order of the contigs.

This is typically a set of paired reads, where the

members of the read pairs are separated by some ap-

proximately known distance. As for assembly, it is

not straightforward to implement a parallel scaffold-

ing algorithm correctly using locking, and commonly

used programs like SSPACE (Boetzer et al., 2011) are

single-threaded.

Scaffolding simpliﬁes the process in two ways:

ﬁrst, it reduces the amount of data that needs to be

considered (E.g. for the sea louse assembly, the ini-

tial assembly involves up to one billion reads). Sec-

ond, mapping reads to contigs make it practical to use

standard alignment tools and ﬁle formats. For these

reasons, the following will focus on the scaffolding

problem.

2 ALGORITHM AND

IMPLEMENTATION

A practical scaffolding program is likely to involve

different heuristics to resolve ambiguous cases in-

cluding repeats and chimeric contigs. As the pur-

pose here is to demonstrate STM as an implementa-

tion technique, we implement a basic scaffolding al-

gorithm that simply links together any pair of con-

tigs that has a mutual best match, as described be-

low. Matches are determined from aligned read pairs

provided as a BAM (The SAM Format Speciﬁcation

Working Group, 2011) ﬁle.

First, the input BAM ﬁle is processed. By examin-

ing read pairs that map to the same contig, we obtain

estimates for the expected distance between paired

reads (called the insert length), and its variance. Also,

the total number of contigs is extracted from the BAM

ﬁle. Simultanously, the alignments relevant for scaf-

folding are extracted. In other words, each read of a

pair must map near the ends of different contigs, and

they must be oriented correctly. These alignments are

stored in an associative data structure.

The scaffolding process uses two arrays, the con-

tig array, which maps each contig to its scaffold, and

the scaffold array, which for each scaffold stores the

scaffold layout, i.e., the set of ordered and oriented

contigs. Initially, each contig is in its own singleton

scaffold.

The program now iterates over all contigs. For

each contig c, the set of read pairs with one mem-

ber matching near the 5’ end of c are extracted. The

Figure 1: An example overlap graph. Two scaffolds are

already identiﬁed,

(blue) containing nodes

, and

and

(red) containing nodes

and

. Adding the edge

(green) from

will merge these into a single scaffold.

Contigs

Scaﬀolds

Contigs

Scaﬀolds

Figure 2: A schematic presentation of the arrays used in the

scaffolding algorithm. As in Fig. 1, contigs

, and

are initially (left) in scaffold

, and contigs

and

are in

scaffold

. When the algorithm decides that contigs

and

(indicated by arrows) should be adjacent, the scaffolds are

merged, causing several cells to be updated (shaded, right).

contig c

to which the largest number of the mapped

reads’ mates map is identiﬁed. If this relationship is

reciprocal (i.e, the reads pairs that map to c

have a

majority of mates mapped to c), the contigs c and c

are merged. The procedure is then applied similarly

to the 3’ end of c.

For instance, in the example graph in Figure 1, ex-

amination of node

has determined that most mapped

reads link it to

, and conversely, most reads mapping

link it back to

. This causes these two contigs

to identiﬁed as adjacent, and their scaffolds are con-

sequently merged.

Merging two scaffolds involves updating one scaf-

fold’s entry in the scaffold array to contain the new

scaffold, and deleting the other scaffold’s entry (see

Figure 2). Then, the elements in the contig array cor-

CanSoftwareTransactionalMemoryMakeConcurrentProgramsSimpleandSafe?

225

responding to contigs in the scaffold that was deleted

are updated to point to the new scaffold.

To parallelize, we simply split the iteration of

the contig array so that each thread iterates over an

equally sized segment of the array. Note that even

if threads work on separate array segments, they will

affect contigs outside their segment.

Statistically, the merging operations will usually

be independent if the arrays are large compared to

the number of concurrent operations (threads). This

also depends on the locality of merging criteria. The

current implementation considers a subgraph consist-

ing of three contigs at a time, but it could be ex-

tended to examine several candidates and links, in ef-

fect making the decision depend on a larger subset

of the graph. This would increase the chance of col-

liding operations. In any case, collisions will occur

occasionally, and a parallel implementation must take

them into account.

STM here makes this process easy, and in fact,

the code implementing this algorithm using mutable

arrays in the IO monad and using transactions in the

STM monad is exactly the same. Only the top-level

function is different, as the STM version must spawn

multiple threads that process an array segment each.

3 RESULTS

In order to test the implementation, the contigs re-

sulting from the assembly of sea louse (Lepeoph-

theirus salmonis) sequences were used. This as-

sembly was constructed using the Newbler program

(Roche), which assembled approximately 50 million

454 reads (Margulies et al., 2005) into 292421 con-

tigs.

As our pairing data, we use a set of 72 200 652 Il-

lumina reads, where each pair consists of two 100bp

reads, spaced about 150bp apart. The reads were

aligned using BWA (Li and Durbin, 2009), resulting

in 68 569 814 alignments (95% of the reads), of these

10 187580 alignments mapped the read and its mate

to different contigs.

The program was compiled with GHC 7.0.2, us-

ing the

-O2

option. It was executed on a computer

with eight Intel Xeon E7340 processors, using options

+RTS -A100M

. The parallel STM version was addi-

tionally compiled with

-threaded

, and run with

-qg

Figure 3 shows the running time for the scaffold-

ing stage. We see that there is some overhead associ-

ated, both with using arrays of transactional variables

(

TArray

) over regular mutable arrays (

IOArray

), and

with running on the multi-threaded GHC run-time

over the single-threaded one.

100

150

200

250

300

350

400

Array STM-S STM-1

Scaffolding time (seconds)

Figure 3: Speed spent in the scaffolding stage. “Array” is

the implementation using mutable arrays, “STM-S” is the

STM implementation running on the single-threaded run-

time, and “STM-1” is the STM implementation using a sin-

gle thread with the threaded run-time.

1 2 4 8 16

Scaffolding speedup

Threads

Figure 4: Speedup of the STM implementation with in-

creasing number of threads. The blue line indicates the rel-

ative performance of the non-STM (“Array”) implementa-

tion.

The STM implementation scales well. From Fig-

ure 4, we see that as we increase the number of par-

allel threads, the speedup is close to the optimum, up

to eight threads, matching the number of CPUs. The

CPUs use hyperthreading, and each processor core

appear to the OS as two processing units. Thus, the

STM implementation is still achieving a substantial

speedup going from 8 to 16 threads, even though it

means running two threads per physical core.

The resulting scaffolds were checked against scaf-

folds produced by SSPACE, and were found to differ

slightly, but for the most part, they identiﬁed the same

layout of contigs.

BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

226

4 DISCUSSION AND

CONCLUSIONS

Software transactional memory is most attractive

when the program can be structured as set of mostly-

independent operations, and where each operation

only involves a small set of variables. If the oper-

ations are completely independent, the problem most

likely can be trivially partitioned, and if the number of

variables involved in each operation is large, perfor-

mance will deteriorate as the transaction log increases

in size.

The overlap-layout-consensus approach to the se-

quence assembly problem ﬁts well with these criteria,

and is well suited to an STM approach. In the im-

plementation presented, we observe a small overhead

for using software transactional memory compared to

regular arrays, and an additional overhead for using

a multi-threaded implementation compared to a sin-

gle threaded one, but the STM implementation scales

well with the number of threads, and already with two

threads it is substantially faster. Although the results

here are very promising, it remains to be seen how far

they generalize, both as the number of CPUs increase,

and to variations of the algorithm.

This analysis has concentrated on how to improve

the run-time performance of the scaffolding process.

This is an important goal in itself, but it is even

more important to improve the quality of the result-

ing genome assembly.

The composability of STM lets the programmer

easily refactor the program or otherwise modify the

algorithm without introducing deadlocks or other syn-

chronization problems. For instance, the current

implementation only considers the potential nearest

neighbors of each contig. Extending it to take into ac-

count a larger subgraph is one possibility in improv-

ing the result. With a traditional locking scheme, this

would likely increase the complexity substantially.

With STM, it would at worst increase the chance of

collisions between transactions, leading to more re-

tries, and consequently a slightly slower program.

The source code for the implementation is avail-

able

under the General Public License.

REFERENCES

454 Life Sciences Corp. (2010). 454 Sequencing System

Software Manual, v 2.5p1, part C. 454 Life Sciences

Corp., Branford, CT 06405.

http://malde.org/∼ketil/biohaskell/stmasm

Boetzer, M., Henkel, C. V., Jansen, H. J., Butler, D., and

Pirovano, W. (2011). Scaffolding pre-assembled con-

tigs using SSPACE. Bioinformatics, 27:578–579.

Bonﬁeld, J. K., Smith, K. F., and Staden, R. (1995). A

new DNA sequence assembly program. Nucleic Acids

Research, 23:4992–4999.

Brevnov, E., Dolgov, Y., Kuznetsov, B., Yershov, D.,

Shakin, V., Chen, D.-Y., Menon, V., and Srinivas, S.

(2008). Practical experiences with java software trans-

actional memory. In Proceedings of the 13th ACM

SIGPLAN Symposium on Principles and practice of

parallel programming, PPoPP ’08, pages 287–288,

New York, NY, USA. ACM.

Harris, T., Marlow, S., Peyton-Jones, S., and Herlihy,

M. (2005). Composable memory transactions. In

Proceedings of the tenth ACM SIGPLAN symposium

on Principles and practice of parallel programming,

PPoPP ’05, pages 48–60, New York, NY, USA. ACM.

Lee, E. A. (2006). The problem with threads. Technical

Report UCB/EECS-2006-1, EECS Department, Uni-

versity of California, Berkeley. The published version

of this paper is in IEEE Computer 39(5):33-42, May

2006.

Li, H. and Durbin, R. (2009). Fast and accurate short read

alignment with burrows-wheeler transform. Bioinfor-

matics, 25:1754–1760.

Margulies, M., Egholm, M., Altman, W. E., Attiya, S.,

Bader, J. S., et al. (2005). Genome sequencing in mi-

crofabricated high-density picolitre reactors. Nature,

437:376–380.

Myers, E. W., Sutton, G. G., Delcher, A. L., Dew, I. M.,

Fasulo, D. P., Flanigan, M. J., et al. (2000). A

whole-genome assembly of drosophila. Science,

287(5461):2196–2204.

Ni, Y., Welc, A., Adl-Tabatabai, A.-R., Bach, M.,

Berkowits, S., Cownie, J., Geva, R., Kozhukow, S.,

Narayanaswamy, R., Olivier, J., Preis, S., Saha, B.,

Tal, A., and Tian, X. (2008). Design and implementa-

tion of transactional constructs for c/c++. In Proceed-

ings of the 23rd ACM SIGPLAN conference on Object-

oriented programming systems languages and appli-

cations, OOPSLA ’08, pages 195–212, New York,

NY, USA. ACM.

Pevzner, P. A., Tang, H., and Waterman, M. S. (2001).

An eulerian path approach to dna fragment assem-

bly. Proceedings of the National Academy of Sciences,

98(17):9748–9753.

Shavit, N. and Touitou, D. (1995). Software transactional

memory. In Proceedings of the fourteenth annual

ACM symposium on Principles of distributed comput-

ing, PODC ’95, pages 204–213, New York, NY, USA.

ACM.

The SAM Format Speciﬁcation Working Group (2011). The

SAM Format Speciﬁcation.

APPENDIX

The code for the merging operation (as illustrated in

Figure 2 is given below. Note that the type signature is

CanSoftwareTransactionalMemoryMakeConcurrentProgramsSimpleandSafe?

227

not given, and the code will typecheck and run with-

out modiﬁcation in either the IO monad or the STM

monad. In STM, each array cell is a TVar, and the

merge operation must be part of a transaction. If an-

other thread modiﬁes any of the involved array loca-

tions before the transaction completes (say by merg-

ing one of the clusters with a different cluster), the

transaction will be aborted and restarted. In IO, there

are no such guarantees, and the function can only be

run safely in a single thread.

The function takes as input parameters arrays of

contigs (each pointing to a cluster) and scaffolds

(echo containing the list of its elements), and a pair

of contigs. It then merges the scaffolds that contain

the given each contig from the pair.

merge contigs scaffolds (contig1,contig2) = do

-- Get the scaffolds for each contig

i1 <- readArray contigs contig1

i2 <- readArray contigs contig2

when(i1/=i2) $ do

-- read counts and elements from clusters

(n1,cs1) <- readArray scaffolds i1

(n2,cs2) <- readArray scaffolds i2

-- write the merged cluster in i1,

-- and an empty cluster in i2

writeArray scaffolds i1 (n1+n2,cs1++cs2)

writeArray scaffolds i2 (0,[])

-- update previous elements in i2

-- to point to the merged cluster

mapM_ (\x -> writeArray contigs x i1) cs2

BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

228