Locally Oriented Anisotropic Image Diffusion:

Application to Phenotyping of Seedlings

Landry Benoit

, David Rousseau

Etienne Belin

, Didier Demilly

Franc¸ois Chapeau-Blondeau

and Carolyne Durr

Laboratoire d’Ing

enierie des Syst

emes Automatis

es (LISA),

Universit

e d’Angers, 62 avenue Notre Dame du Lac, 49000 Angers, France

Universit

e de Lyon, CREATIS, CNRS UMR 5220, INSERM U1044,

Universit

e Lyon 1, INSA-Lyon, 69621 Villeurbanne, France

GEVES, Station Nationale d’Essais de Semences (SNES),

rue George Morel, 49071 Beaucouz

e, France

INRA, UMR 1345, IRHS, 42 rue Georges Morel, 49071 Beaucouz

e, France

Abstract. A variant of the Perona-Malik anisotropic diffusion equation is in-

troduced for the segmentation of multiple objects with crossings. The diffusion is

automatically applied at the crossings locations along the main orientations of the

objects. Application of this process is given for illustration on an original prob-

lem of plant imaging with the monitoring of the elongation of multiple crossing

seedlings.

1 Introduction

Since its introduction some 3 decades ago by Perona and Malik [12] partial differen-

tial equations (PDE) as a mathematical framework for image processing have raised a

considerable attention [14]. This interest is mathematically motivated by the possibility

of a variational interpretation of the action of the PDE. Also, PDE inspired by physi-

cal modeling constitute a vast ﬁeld of investigation to be considered for its own sake

or for new approaches to various image processing applications (restoration, segmen-

tation, in-painting, to name few areas where PDE have been competitively applied). In

this report, we revisit the recently introduced oriented diffusion equation [5] where a

diffusion process is applied to an input image with a selective function of the angle

between the local gradient and a global orientation of reference. For gradient along

the reference, there is no diffusion, while gradients perpendicular to the reference are

associated to maximal diffusion. As such, the oriented diffusion equation of [5] is in-

teresting when a single direction is taken as reference for the whole image. This is the

case in the tagged grid MRI sequence considered for illustration in [5]. However, there

are practical situations where a selective diffusion process would be useful if applied

with a local orientation of reference. This is the case when the targeted information

task is the individual restoration of multiple objects crossing with various angles. As an

extension of [5] we therefore propose a locally oriented anisotropic diffusion process

with a local orientation of reference at the scale of an imagette. We demonstrate the

usefulness of this approach with an original bioimaging application. The report is orga-

nized as follows. We ﬁrst describe the orientation diffusion equation of [5] and discuss

Benoit L., Rousseau D., Belin É., Demilly D., Chapeau-Blondeau F. and Dürr C..

Locally Oriented Anisotropic Image Diffusion: Application to Phenotyping of Seedlings.

DOI: 10.5220/0004330100030009

In Proceedings of GEODIFF 2013 (GEODIFF-2013), pages 3-9

ISBN: 978-989-8565-49-5

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

the limitation of this approach in the case of our plant imaging application. We then

introduce our new anisotropic diffusion equation and illustrate its performance on our

application.

2 Locally Oriented Anisotropic Diffusion

Anisotropic diffusion applied in image processing has been introduced in [12]. It is a

process inspired from the physics of temperature diffusion in which an input image

is transformed in an output image ψ taken as the solution of the partial differential

equation given by

∂ψ

∂t

= div(g(k∇ψk)∇ψ), ψ(x, y, t = 0) = ψ

. (1)

The anisotropy of this diffusion process is governed by g(.) a nonlinear decreasing func-

tion of the norm of the gradient ∇ψ. Function g(.) is a nonlinear decreasing function

g(u) = exp



−



, (2)

in the original work of [12] where parameter k can be seen as a soft threshold controlling

the decrease of g(.) and the amplitude of the gradients to be preserved from the diffusion

process. Many variants of the diffusion process of Eq. (1) have been proposed (see [14]

for a review). The beneﬁt of such diffusion processes lies in the ability to smooth data

in a nonlinear way, while preserving important image features (contours, corners, . . . ).

Recently an oriented variant of the anisotropic diffusion process of Eq. (1) has been

proposed in [5] to control the diffusion process with the direction of the gradient instead

of only the norm of the gradient. The partial differential equation of [5] reads

∂ψ

∂t

= div(g(A.∇ψ)∇ψ), ψ(x, y, t = 0) = ψ

, (3)

where A is a vector ﬁeld deﬁning the particular direction to preserve from the diffu-

sion process. In [5] application of Eq. (3) was given in a case where the vector ﬁeld

A was selecting a single direction in a whole single image. In certain situations the di-

rections to be preserved can spatially change in the image. This is for instance the case

with the separation of multiple crossing objects in image. Crossing objects appear in

various ﬁelds of science like for instance vessel or muscle ﬁbers crossing in biomed-

ical imaging [4,8,2], crossings roads in remote sensing [9], or assemblies of crossing

nano-objects with microscopes in physics [3]. The restoration of each object in such

images of crossing objects is an important problem if one is interested in performing

individual measurements on each object. In this work, we consider this crossing objects

problem with the oriented anisotropic diffusion of Eq. (3). In [5] illustration is given

with a unique direction in the vector ﬁeld. To deal with multiple crossing objects, we

have implemented a locally oriented anisotropic diffusion process that preserves a local

orientation of reference at the scale of an imagette. To this purpose, we propose to per-

form a crossing detection before applying diffusion. We then apply the diffusion process

of Eq. (3) locally only in the vicinity of the crossing objects. The crossing is character-

ized by two directions. The idea is to diffuse in one of these directions to restore and

Fig. 1. Sequence of acquired images with green backlight during seedling elongation with a 2

hour time step between each snapshot A, B, C and D. The typical duration of the elongation

process can be several days.

segment one object and then to repeat this process in the other direction to restore the

other object. We apply this strategy to a real world problem from plant science in the

next section. For illustration in this work we have taken as in [6] the nonlinear function

g(.) in Eq. (3) as a hard threshold

g(u) =



0 for u ≥ k

1 for u ≤ k .

(4)

With this choice the diffusion process simply corresponds to a threshold on the gradients

oriented in the direction of the vector ﬁeld A. Gradients oriented in the correct direction

are preserved while other direction are erased. This is obtained in one iteration in the

diffusion equation.

3 Application to Seedling Elongation

Seedling elongation is an early stage of the development of plants. During this stage,

the seed is in the soil. Following a geotropism, the upper part of the seedling grows

to reach the light and activates photosynthesis while the lower part of the seedling is

going deeper to anchor in the soil and access to water and nutrients. In ﬁeld conditions

this seedling elongation is not accessible to plant analysts. However, non invasive mon-

itoring of seedling growth is accessible in vitro with computer vision machines [11, 7,

13,15], French et al., 2011, [1]. A set of seedlings can for instance be positioned on

an horizontal row in a gelose box. A backlight system associated with a camera then

produces sequences of images like in Fig. 1. From such image sequences, the temporal

evolution of the length of the radicle of the seedling is measurable with classical binary

image skeletonisation [11, 7, 13,15], French et al., 2011, [1]. However, other traits like

the respective size of the organs of the seedling are not accessible from the skeleton and

require more elaborated image processing approaches. A difﬁculty visible in the images

of Fig. 1 is that the radicle of the seedlings can cross. To overcome this difﬁculty we

propose the following pipeline including the diffusion process of Eq. (3) implemented

in the algorithm of Fig. 2. In the images of Fig. 1 the seedlings are well-contrasted from

the background. The segmentation of the seedlings can thus be done after a simple

thresholding. The resulting binary image is skeletonized. Crossings are detected in this

skeleton around points of the skeleton having connectivity higher than two. Regions of

interest including a single crossing are then deﬁned. Such a region of interest serves as

input to the algorithm detailed in Fig. 2.

Fig. 2. Four steps seedling crossing segmentation algorithm. In a ﬁrst step the algorithm load

(A) an input binary image corresponding to a crossing in the input image. (B) Histograms of

the orientation of the gradients are calculated. Two main directions of the crossing are present

in this histogram. The diffusion equation of Eq. (3) is consecutively applied in each one of these

two main directions to produce two images preserving the respective other direction (C). The

threshold k in Eq. (4) is consecutively chosen equal to the main directions of each modes in the

histogram in (B). In the second step, the holes in the binary images are ﬁlled (D). A seedling

crossing map is created in (E-F) in a third step and the seedlings are labeled (G) in the fourth

step.

As illustrated in Fig. 3, seedlings crossing in the sequence are correctly separated.

We have tested successfully the algorithm of Fig. 2 on various species including species

with several seminal roots like wheat. In these cases crossings are very common and

separating the different roots is crucial. Finally, the good performance of our algorithm

in this study is important for two reasons. First it enables to perform the elongation

monitoring at more advanced stages of development. Second this enables to concentrate

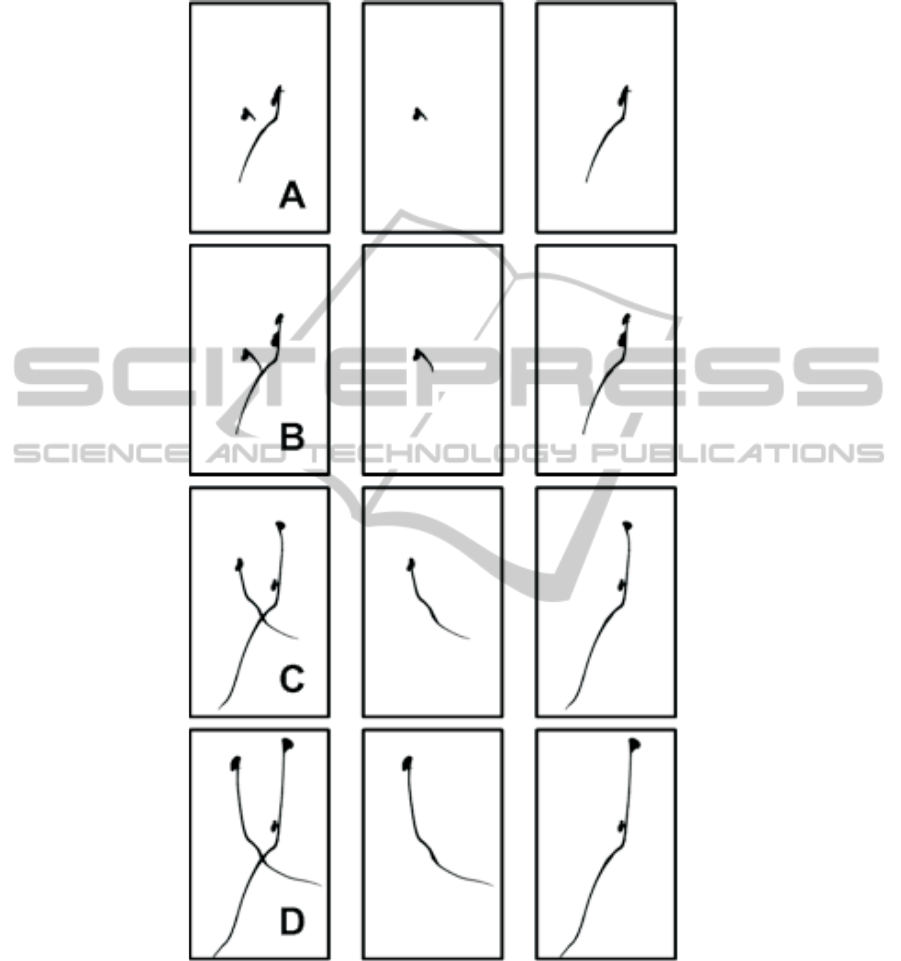
Fig. 3. Results of our crossing seedlings segmentation on two crossing seedlings of the image

sequence of Fig. 1. In the left column a binarized version of a crop form Fig. 1 at instant A, B C

and D. The two other columns represent the output of the algorithm of Fig. 2 with the two labeled

seedlings.

higher number of seeds of different types of species in the ﬁeld of view of the camera

and therefore contributes to increase the throughput of the monitoring.

4 Conclusions

In this work we have presented an extension of the partial differential equation of [5].

In our case, a detection of the part which requires to be diffused is ﬁrst performed and

the partial differential equation is then applied locally only in these parts. This presents

the interest to speed up the diffusion process by comparison to a global approach. This

also avoids diffusion artefacts in areas where no diffusion was needed. Application of

our PDE was given here for illustration in the domain of plant science with crossing

seedlings during their elongation stage. In our case the segmentation of the crossing

seedlings was obtainable from a simple threshold and the partial differential equation

was only applied in the crossings area to separate the seedlings. However, for some

species with very thin roots, the contrast between background and seedlings may not

be so favorable and it could be interesting to apply the oriented anisotropic diffusion

locally in the whole image to separate seedling around crossings and also to restore the

edges along the curvated roots in non crossing areas. Plants are highly anisotropic struc-

tures organized along branching structures. Plants growth or plant pathogens spreading

along these structures therefore constitute a natural ﬁeld of applications for anisotropic

diffusion with PDE to analyze or modelize these spatio-temporal phenomenon.

Acknowledgements

The work received support from the ANR in the framework of the AKER Investissements

d’Avenir project. Landry BENOIT thanks Angers Loire M

etropole and SNES-GEVES

for ﬁnancial support of his PhD Grant.

References

1. Belin, E., Rousseau, D., Rojas-Varela, J., Demilly, D., Wagner, M., Cathala, M., and Durr, C.

(2011). Thermography as non invasive functional imaging for monitoring seedling growth.

Computers and Electronics in Agriculture, 79:236–240.

2. B

odvarsson, B., Klim, S., Morkebjerg, M., Yoon, S. M. C., Chen, J., Maclaren, J., Luther, P.,

Squire, J., Bones, P., and Millane, R. (2008). A morphological image processing method for

locating myosin ﬁlaments in muscle electron micrographs. Image and Vision Computing,

26:1073–1080.

3. Chainais, P. and Lebental, B. (2011). Caract

erisation statistique d’une assembl

ee de nan-

otubes en imagerie microscopique. Actes du 23

eme Colloque GRETSI sur le Traitement du

Signal et des Images, Bordeaux, France, 8-11 sept. 2011.

4. Frangi, A., Niessen, W., Vincken, K., and Viergever, M. (1998). Multiscale vessel enhance-

ment ﬁltering. Lecture Notes in Computer Science, Springer, Berlin, pages 130–137.

5. Histace, A., M

enard, M., and Cavaro-M

enard, C. (2009). Selective diffusion for oriented

pattern extraction: Application to tagged cardiac MRI enhancement. Pattern Recognition

Letters, 30:1356–1365.

6. Histace, A. and Rousseau, D. (2010). Noise-enhanced nonlinear PDE for edge restoration

in scalar images. 2nd IEEE Conference on Soft Computing and Pattern Recognition, Cergy,

France, 7-11 dec. 2010.

7. Kimura, K. and Yamasaki, S. (2003). Accurate root length and diameter measurement using

nih image: use of pythagorean distance for diameter estimation. Plant and Soil, 254:305–315.

8. Kirbas, C. and Quek, F. (2003). Vessel extraction techniques and algorithms : a survey.

3rd IEEE Symposium on Bioinformatics and Bioengineering, Bethesda, USA, 10-12 march

2003, pages 238–245.

9. Laptev, I., Mayer, H., Lindeberg1, T., Eckstein, W., Steger, C., and Baumgartner, A. (2000).

Automatic extraction of roads from aerial images based on scale space and snakes. Machine

Vision and Applications, 12:23–31.

10. Naeem, A., French, A., Wells, D., and Pridmore, T. (2011). High-throughput feature counting

and measurement of roots. Bioinformatics, 27:1337–1338.

11. Nagy, F. and Schafer, E. (2002). Phytochromes control photomorphogenesis by differentially

regulated, interaction signaling pathways in higher plants. Annual Review of Plant Biology,

53:329–355.

12. Perona, P. and Malik, J. (1990). Scale-space and edge detection using anistropic diffusion.

IEEE Transactions on Pattern Analysis and Machine Intelligence, 12:629–639.

13. Wang, L., Assadi, A. H., and Spalding, E. P. (2009). Tracing branched curvilinear structures

with a novel adaptive local PCA algorithm. Plant Physiology, 53:1632–1637.

14. Weickert, J. (1998). Anisotropic Diffusion in Image Processing. Teubner-Verlag, Stuttgart.

15. Yazdanbakhsh, N. and Fisahn, J. (2010). Analysis of arabidopsis thaliana root growth kinet-

ics with high temporal and spatial resolution. Annals of Botany, 105:783–791.