
Rotated Local Binary Pattern (RLBP)
Rotation Invariant Texture Descriptor
Rakesh Mehta and Karen Egiazarian
Tampere University of Technology, Tampere, Finland
Keywords:
Texture Descriptor, Local Binary Pattern (LBP), Rotation Invariance, Local Descriptor.
Abstract:
In this paper we propose two novel rotation invariant local texture descriptors. They are based on Local
Binary Pattern (LBP), which is one of the most effective and frequently used texture descriptor. Although
LBP efficiently captures the local structure, it is not rotation invariant. In the proposed methods, a dominant
direction is evaluated in a circular neighbourhood and the descriptor is computed with respect to it. The
weights associated with the neighbouring pixels are circularly shifted with respect to this dominant direction.
Further, in the second descriptor, the uniformity of the patterns is utilized to extract more discriminative
information. The proposed methods are tested for the task of texture classification and the performance is
compared with original LBP and its existed extensions.
1 INTRODUCTION
Texture classification is an important area of research
in computer vision and pattern recognition. The
texture based descriptors have been used for object,
scene and face classification. A number of approaches
can be found in literature based on filter banks (Salas
and Hille, 1978), co-occurrence statistics (Haralick,
1979), local scale (Ojala et al., 2002) and more re-
cently, on keypoints based setting (Ling and Soatto,
2007) and multi fractal schemes (Xu et al., 2009).
Among them, Local Binary Pattern (LBP) (Ojala
et al., 2002) has gained a popularity due to compu-
tational simplicity and good performance. The origi-
nal LBP operator is invariant to monotonic gray scale
changes as it is computed by taking a difference of the
pixels intensities. However, it is not invariant to im-
age rotations. A number of extensions of LBP have
been proposed to incorporate the rotation invariance
property into it. Ojala et. al. proposed LBPROT
which circularly shifts the binary code until it cor-
responds to one of the preselected rotation invariant
patterns (Ojala et al., 2002). This approach, how-
ever, loses a discriminative information because of
the non-uniformity of the pattern density in the im-
age. To retain the global information Li et. al. pro-
posed a circular shifting of the histogram bins with
respect to the largest bin, since it corresponds to the
most frequent pattern in the image (Li et al., 2012).
Gou et. al. combined the information related to the
g
1
g
0
g
7
g
6
g
2
g
5
g
3
g
4
2
1
128
64
4
32
8
16
g
c
a b
Figure 1: (a) The neighbourhood for LBP (b) Weights asso-
ciated with the neighbours.
magnitude and central pixel that is complementary to
the sign values (Guo et al., 2010a). They also pro-
posed to estimate the principle orientation and then
align the LBP features with respect to this orientation
(Guo et al., 2010b). Recently Zhao et. al. proposed
LBP Histogram Fourier (LBP-HF) descriptor (Zhao
et al., 2012), that computes the discrete Fourier trans-
form over the histograms to achieve rotation invari-
ance. The Fourier transform, however, completely
ignores the structural arrangement of the histogram,
thereby losing some discriminative information.
In all above mentioned approaches the rotation
invariance is achieved at the expense of losses of
some discriminative features extracted using original
LBP. These losses occur due to the compact map-
ping (Ojala et al., 2002), transformation of histograms
(Zhao et al., 2012) or shifting of the histograms bins
(Li et al., 2012). In this paper we propose a frame-
work which can incorporate the complete structural
497
Mehta R. and Egiazarian K. (2013).
Rotated Local Binary Pattern (RLBP) - Rotation Invariant Texture Descriptor.
In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 497-502
DOI: 10.5220/0004334304970502
Copyright
c
SciTePress

221
53
170
202
43
55
44
52 127
1
0
1
1
0
0
0
0
2
1
128
64
4
32
8
16
170
20
2
55
52
53
44
221
43 127
1
1
0
0
0
0
1
0
2
1
128
64
4
32
8
16
a
b
c
d
11
194
e
Figure 2: Effect of rotation on LBP operator (a) The image (top) and 90
0
counter-clockwise rotated image (bottom), (b) In
the rotated images the neighbourhood is rotated counter-clockwise by 90
0
, (c) Values above threshold are shown in red color,
(d) The weights corresponding to the thresholded neighbours, (e) LBP values.
information extracted by LBP and, at the same time,
achieve a rotation invariance. The main idea behind
the paper is to set a local reference direction in ev-
ery circular neighbourhood and compute the descrip-
tor with respect to it. When the image is rotated, the
local reference direction is also subjected to the rota-
tion by the same degree, hence, the descriptor com-
puted with respect to it remains the same. The choice
of local reference, instead of a global one, is moti-
vated by the fact that the texture is a local cue and is
computed locally by LBP. Usage a single global ref-
erence for a whole image may lead to computation of
LBPs which are misaligned.
This paper starts with a discussion on the reason-
ing behind the inability of LBP to deal with a rotation
changes. Then we introduce the idea of dominant di-
rection, which is used as the reference while comput-
ing the local descriptor. Based on this idea we propose
novel descriptors RLBP and uRLBP. RLBP is com-
puted by circularly shifting the binary code at each
location based on the dominant direction. uRLBP is
an extension of RLBP, utilizing the concept of uni-
form pattern. The proposed descriptors are easy to
compute and with a relatively less number of neigh-
bours they achieve a good performance.
The rest of the paper is organized as follow. In
Section 2 we discuss the LBP operator on rotated
images. In Section 3, we present the proposed ap-
proach for a texture classification based on two novel
descriptors RLBP and uRLBP. The experiments are
performed on the standard texture datasets to com-
pare the performance of the proposed methods with
the existed ones. The results are reported in Section 4
and, finally, the paper is concluded in Section 5.
2 LBP ON ROTATED IMAGES
LBP operator is computed in a local circular region by
taking the difference of the center pixel with respect
to its neighbours. It is defined as
LBP
R,P
=
P−1
∑
p=0
s(g
p
− g
c
) · 2
p
, (1)
s(g
p
− g
c
) =
1 g
p
≥ g
c
0 g
p
< g
c
. (2)
where g
c
and g
p
denote the gray values of the cen-
tral pixel and its neighbour, respectively, p is the in-
dex of the neighbour, R is the radius of the circu-
lar neighbourhood and P is the number of the neigh-
bours. Fig. 1 shows the neighbours for P = 8 and
the weights corresponding to these neighbours. If the
coordinate of the central pixel is (x,y), then the coor-
dinates of uniformly spaced circular neighbourhood
are given as (x + Rcos(2πp/P),y − Rsin(2πp/P)) for
p = 0,1,2,...,P − 1. If the neighbouring coordinate
does not correspond to integer values, then bilinear
interpolation is used for estimation of pixel value.
Further, to extract the most fundamental struc-
ture from the LBP, the idea of uniform pattern is uti-
lized. A local binary pattern is called uniform if bi-
nary code contains at most two transitions from 0 to
1 or vice versa. For example, the patterns 00011100,
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
498

01000000 are uniform as both consist of 2 transitions,
while 00101000 and 00011010 are non-uniform as
they contain 4 transitions. In practice, this is imple-
mented using a lookup table of elements where the
table maps the non-uniform patterns into a single bin
and all others separately. For P neighbours, the num-
ber of uniform LBP patterns is given by P(P − 1)+ 3.
The LBP operator takes the difference of the cen-
tral pixel with the neighbouring pixels and combines
the signs of these differences using unique weights.
The order of the weights is fixed in the circular neigh-
bourhood, i.e. the weight corresponding to g
0
is al-
ways 1 and so on, as it is shown in Fig. 1. If the im-
age undergoes a rotation, the arrangement of the pixel
around the center undergoes a shift. Since the order of
the weights is fixed, the LBP computed on the rotated
images is unable to deal with the rotation changes.
Thus, even for a simple image rotation the LBP oper-
ator provide very different values. Fig. 2 shows the
effect of rotation on the LBP operator. In this illus-
tration LBP is computed at some location in image
and on a rotated version of the same image. As image
is rotated counter-clockwise by 90
0
, the neighbours
around each pixel also undergo a counter-clockwise
rotation of the same angle as shown in Fig. 2(b). The
pixels in the circular neighbourhood are thresholded
with respect to the central pixel and those above the
threshold are shown in red color in Fig. 2(c). The
weights corresponding to these pixel values are also
highlighted in red color in Fig. 2(d). The thresholded
pixels and weights in both images correspond to very
different locations and when summed up this results
in distinct output values. It is due to the fact that the
arrangement of the weights in LBP does not depend
on the values of the neighbours. In order to overcome
this problem we propose to adaptively select the ar-
rangement of the weights based on the values of pix-
els in the neighbourhood.
3 TEXTURE CLASSIFICATION
USING RLBP
In this section we present the proposed approach for
the task of texture classification. First, we intro-
duce RLBP operator obtained by circularly shifting
the weights of LBP operator. Further, the intrin-
sic structure of the patterns is utilized by incorporat-
ing the principle of uniform patterns to generate uni-
form RLBP (uRLBP). Finally, two classifiers (nearest
neighbour (NN) and support vector machine (SVM))
are discussed along with their choice of parameters.
3.1 Rotated Local Binary Pattern
(RLBP)
LBP only considers the signs of the differences to
compute the final descriptor. The information related
to the magnitude of the differences is completely ig-
nored. The magnitude provides a complimentary in-
formation that has been utilized (Guo et al., 2010a)
to increase the discriminative power of the operator.
Especially in the neighbourhood with strong edges
the magnitude of the differences can provide an im-
portant information. Here we utilize the magnitude
of the difference to find the dominant direction in a
neighbourhood. The dominant direction is defined as
the index in the circular neighbourhood for which the
difference is maximum. As an image undergoes a ro-
tation the dominant direction in a neighbourhood also
undergoes the rotation by the same angle. In the pro-
posed descriptor the dominant direction is set as the
reference and the weights for the neighbourhood are
arranged with respect to it.
In order to make the LBP invariant to rotation we
circularly shift the weights according to the dominant
direction. The dominant direction (D) in a neighbour-
hood is the index of neighbour whose difference to
the central pixel is maximum; it is defined as
D = argmax
p∈(0,1...P−1)
|g
p
− g
c
|. (3)
The rotation of neighbourhood with respect to its cen-
ter shifts the direction D by the same angle. For ex-
ample, if we consider a neighbourhood [23 25 28;
167 35 31; 56 67 72], after the thresholding its bi-
nary code is [01111000], the index of D is 4 (shown
in bold) corresponding to the pixel value 167 . If the
image is rotated by 45
0
counter-clockwise, then the
neighbourhood also rotates by the same angle and the
binary code shifts to [00111100]. D index still cor-
responds to the same value (167) but it shifts by one
step. However, the circular arrangement of the pix-
els in the neighbourhood remains the same with re-
spect to the direction D. Therefore the lowest weight
is associated with the index corresponding to D and is
subsequently increased in the counter-clockwise di-
rection.
Since the dominant direction is taken as the ref-
erence in the circular neighbourhood, the weights are
assigned with respect to it. Thus the RLBP operator
is defined as
RLBP
R,P
=
P−1
∑
p=0
s(g
p
− g
c
) · 2
mod(p−D,P)
, (4)
where mod indicates the modulus operation. In the
above definition the weight term 2
mod(p−D,P)
depends
RotatedLocalBinaryPattern(RLBP)-RotationInvariantTextureDescriptor
499
221
53
170
202
43
55
44
52 127
1
0
1
1
0
0
0
0
1
128
64
32
2
16
4
8
170
202
55
52
53
44
221
43 127
1
1
0
0
0
0
1
0
64
32
16
8
128
4
1
2
a
b
c
d
97
97
e
Figure 3: Effect of rotation on RLBP operator (a) The image (top) and 90
0
counter-clockwise rotated image (bottom), (b)
Yellow color pixel indicate the dominant direction, (c) Values above threshold are shown in red color, (d) The weights are
circularly shifted with respect to dominant direction, (e) RLBP values.
on D. The weights are circularly shifted with respect
to the dominant direction. The shift results in a ro-
tation invariance, as the weights now depend on the
neighbourhood and not on a preselected arrangement.
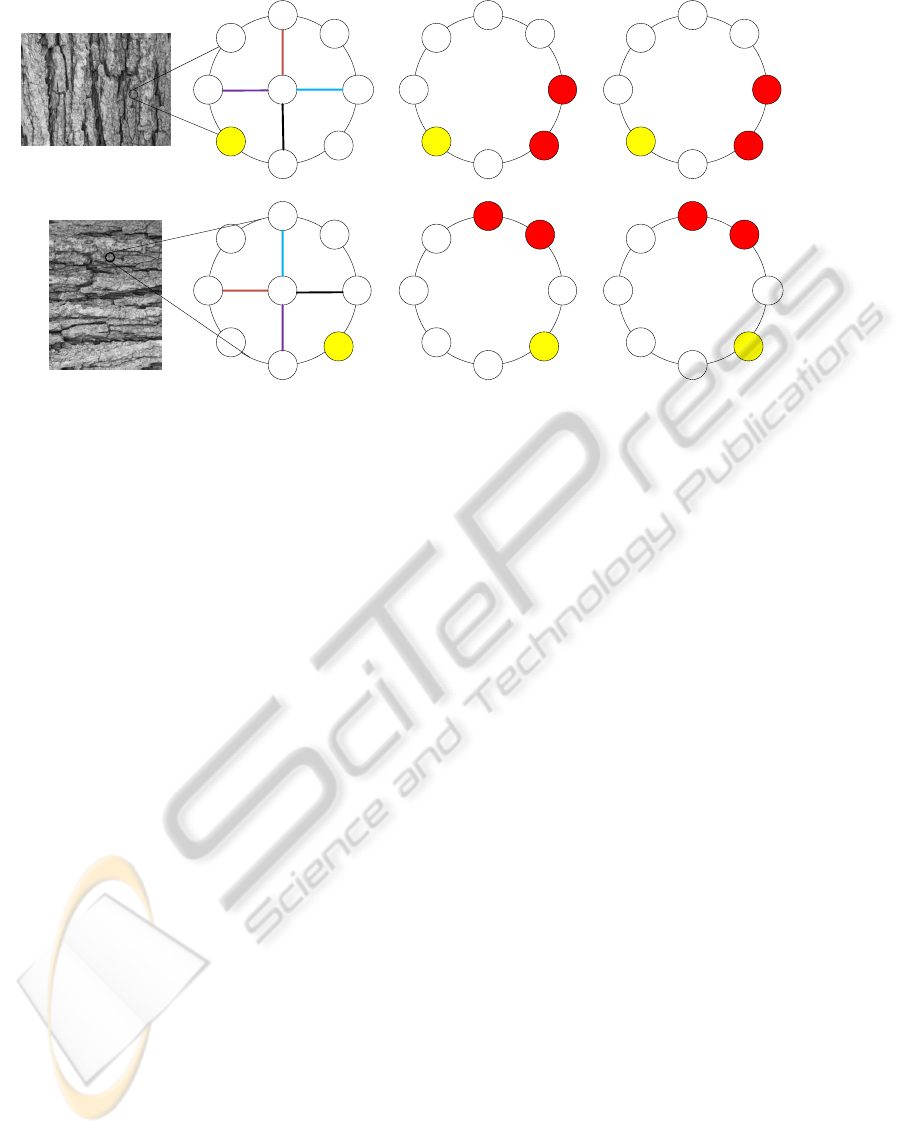
Fig. 3 shows the effect of rotation on the RLBP fea-
tures. For clear understanding we use the same sce-
nario as was used in Fig. 2 for LBP. As before, the red
color indicate the pixels above the threshold, yellow
color indicate the pixel corresponding to the dominant
direction D. The bit corresponding to index D always
takes the lowest weight of 1 and other weights are cir-
cularly shifted with respect to it. In Fig. 3(d) it can
be seen that the weight corresponding to the dominant
position is the same for original and rotated images,
although these pixels are at different locations. Thus
the RLBP values obtained for two different rotated
neighbourhood are similar in this case.
3.2 Uniform Rotated Local Binary
Pattern
To utilize the intrinsic structure of the binary pat-
terns the idea of uniform patterns is applied on the
LBP. The uniform LBP (uLBP) achieves better per-
formance compared to LBP due to the statistical prop-
erties of these patterns. Experiments carried out on
large image datasets showed that up to 90% of the
total patterns are uniform while the remaining small
percentage are non uniform. This small portion of
non-uniform patterns are distributed in large number
of histogram bins which cannot be estimated reliably.
The accumulation of large number of uniform pat-
terns into relatively small number of histogram bins
provides the discriminative information, which is uti-
lized by uLBP. Thus, if the distribution of the patterns
obtained by the operator is preserved, the uniformity
of the pattern can be utilized to enhance the discrimi-
native power.
Similar to the LBP operator, the RLBP operator
computes the binary patterns based on pixel neigh-
bourhood. The final values obtained by these oper-
ators are different because the weights are circularly
shifted in RLBP operator. Since the binary patterns
are same for both operators, the distribution of the
patterns is similar. To capture an additional discrimi-
native information, we apply the idea of the uniform
patterns to RLBP operator. The uniform RLBP opera-
tors is given as U(RLBP
R,P
), where U() is the lookup
table that defines a mapping from a binary pattern to
a uniform pattern. For a neighbourhood of P pix-
els, the lookup table U () consist of 2
P
elements and
P(P − 1) + 3 different output values corresponding to
the uniform patterns.
3.3 Classifiers
The performance of the descriptor is tested by two dif-
ferent classifiers: Nearest Neighbour (NN) and Sup-
port Vector Machine (SVM). The nearest neighbour
classifier is used with a number of different distance
metrics such as chi-square, log-likehood, cosine dis-
tance, etc. In this study we use the histogram inter-
section which is given as
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
500

d(H,K) = 1 −
∑
i
min(h
i
,k
i
)
∑
i
k
i
(5)
where H is the histogram of the test sample, K is the
histogram of the training sample, i represent the bin
number and h
i
, k
i
are the values of the the i
th
bin in
the histogram H and K respectively. The test sample
is assigned to the class of the training sample which
minimizes this distance.
Nearest neighbour is a simple classifer which can
deal with easy rotational variations. However it can-
not effectively model the texture with more difficult
viewpoint and scale variations. Thus, to deal with
these difficult conditions, SVM classifier is utilized.
The SVM classifier is tested with different kernels and
the linear kernels provided the best numerical results.
4 EXPERIMENTS
The proposed method is tested on three different tex-
ture datasets: Outex-10, Outex-12 and UIUC tex-
ture datasets. Outex-10 and Outex-12 have only ro-
tational variation while the UIUC is much more dif-
ficult dataset with rotation, scale and viewpoints vari-
ations. The performance of the proposed algorithm
is compared with LBP, uniform LBP (uLBP), rota-
tion invariant LBP (riLBP), uniform rotation invari-
ant LBP (uriLBP) and LBP-HF.Three of these meth-
ods ((riLBP),(uriLBP) and LBP-HF) are rotation in-
variant version of LBP. To keep the complexity low
we set the number of neighbours to 8 in all the tests.
4.1 Outex-12
Outex-12 dataset consists of 9120 images represent-
ing 24 different textures under different lighting and
rotations. In our experiments, 20 images from each
class are used for training and the rest are used for
testing. Thus, the testing set consists of 8640 images
and training set consists of 480 images. The results of
comparison are shown in Table 1. It can be observed
that the methods proposed specifically to deal with the
rotation changes, such as riLBP, LBP-HF and the pro-
posed descriptor, achieve much better accuracy than
the original LBP. LBP-HF preforms better than ear-
lier proposed descriptors riLBP and uriLBP. However,
the proposed descriptor outperforms this state-of-the-
art rotation invariant LBP-HF. The radius parameter
is increased from 1 to 3 for LBP-HF and RLBP. It is
interesting to observe that for both descriptors the per-
formance improves with an increase in the radius. At
smaller radius the operator captures pixel related in-
formation while at the larger radius the region based
Table 1: Test results for Outex-12 dataset.
Method Accuracy Dimensionality
LBP 54.8 256
uLBP 54.54 59
riLBP 66.40 36
uriLBP 62.23 10
LBP − HF
1,8
75.48 38
LBP − HF
2,8
80.30 38
LBP − HF
3,8
82.97 38
RLBP
1,8
72.35 256
RLBP
2,8
80.88 256
RLBP
3,8
85.68 256
uRLBP
1,8
74.86 59
uRLBP
2,8
83.19 59
uRLBP
3,8
88.01 59
information is captured. For radius 3 the operator cap-
tures the directional information from the circular re-
gions of diameter 7. As the radius is increased further
the accuracy decreases, which implies that for large
region (radius > 3) binary patterns cannot effectively
capture the structure.
4.2 Outex-10
The Outex-10 dataset consists of 4320 images
belonging to 24 different textures classes. The
images are rotated at nine different angles
(0
0
,5
0
,10
0
,15
0
,30
0
,45
0
,60
0
,75
0
,90
0
) and the
illumination is kept constant. In our experiments,
20 images from each class are used for training
and the rest 3840 images are used for testing. The
results are shown in Table 2. LBP and uLBP perform
poorly because they are not designed to deal with
any rotational variations. Their rotation invariant
versions, riLBP and uriLBP, provide much better
results. The best accuracy is again achieved by the
uRLBP with radius 3. The proposed method again
achieves higher accuracy than the recently proposed
LBP-HF which can be attributed to the fact that the
structural information is retained in the RLBP while
in the LBP-HF rotation invariance is achieved at
the loss of the structural information of the binary
patterns.
4.3 UIUC Dataset
In order to test descriptor against more difficult con-
ditions we have used the UIUC texture dataset. This
dataset consist of 1,000 uncalibrated unregistered im-
ages: 40 samples each of 25 different textures. Sig-
nificant rotation, viewpoint changes and scale differ-
ences are present within each class and illumination
RotatedLocalBinaryPattern(RLBP)-RotationInvariantTextureDescriptor
501

Table 2: Test results for Outex-10 dataset.
Method Accuracy Dimensionality
LBP 52.66 256
uLBP 54.19 59
riLBP 83.15 36
uriLBP 84.01 10
LBP − HF
1,8
78.46 38
LBP − HF
2,8
83.46 38
LBP − HF
3,8
87.81 38
RLBP
1,8
86.41 256
RLBP
2,8
89.82 256
RLBP
3,8
90.39 256
uRLBP
1,8
88.07 59
uRLBP
2,8
92.94 59
uRLBP
3,8
95.96 59
conditions are uncontrolled. In our experiments we
use 10 images from each class for training and rest
of the images for testing. The results of the compari-
son are shown in Table 3. Although the descriptor is
not specifically designed to deal with viewpoint and
scale changes, it achieves best performance among
the rotation invariant LBP versions. It can be ob-
served that the performance of other rotation invariant
LBP (uLBP, riLBP and LBP-HF) decreases consid-
erable on this dataset. Proposed descriptor achieves
highest accuracy because it retains the structural in-
formation captured by the original LBP in addition
the rotation invariance helps to deal with the view-
point changes. Also it is interesting to note the role
of uniform pattern in this dataset; for all three de-
scriptors LBP, riLBP and RLBP where uniform pat-
terns are utilized, the accuracy drops by few percent
for their uniform counterpart. In the difficult rotation,
scale and viewpoint variations the small number of
uniform patterns are not sufficient to model the neigh-
bourhood of the pixels.
5 CONCLUSIONS
In this paper we have presented rotation invariant lo-
cal descriptors for texture classification. The opera-
tors utilize information from the local neighbourhood
to achieve a rotation invariance. Under any rotation
transformation the local circular neighbourhood also
undergoes the rotation around its center. However, if
the descriptor is computed by using the local dom-
inant direction as the reference, then it becomes in-
variant to a rotation. Based on this idea we proposed
two rotation invariant descriptors RLBP and uRLBP.
The experiments performed on the standard texture
datasets show that the proposed method performs bet-
Table 3: Test results for UIUC Texture dataset.
Method Accuracy Dimensionality
LBP 50.40 256
uLBP 49.2 59
riLBP 58.00 36
uriLBP 56.13 10
LBP − HF
1,8
59.73 38
LBP − HF
2,8
70.00 38
LBP − HF
3,8
66.40 38
RLBP
1,8
67.06 256
RLBP
2,8
73.60 256
RLBP
3,8
77.47 256
uRLBP
1,8
67.06 59
uRLBP
2,8
72.53 59
uRLBP
3,8
74.53 59
ter than a number of state-of-the-art LBP based rota-
tion invariant descriptors.
REFERENCES
Guo, Z., Zhang, L., and Zhang, D. (2010a). A completed
modeling of local binary pattern operator for texture
classification. Image Processing, IEEE Transactions
on, 19(6):1657–1663.
Guo, Z., Zhang, L., and Zhang, D. (2010b). Rota-
tion invariant texture classification using lbp variance
(lbpv) with global matching. Pattern Recognition,
43(3):706–719.
Haralick, R. (1979). Statistical and structural approaches to
texture. Proceedings of the IEEE, 67(5):786–804.
Li, Z., Liu, G., Yang, Y., and You, J. (2012). Scale-
and rotation-invariant local binary pattern using
scale-adaptive texton and subuniform-based circular
shift. Image Processing, IEEE Transactions on,
21(4):2130–2140.
Ling, H. and Soatto, S. (2007). Proximity distribution ker-
nels for geometric context in category recognition. In
IEEE ICCV., pages 1–8.
Ojala, T., Pietikainen, M., and Maenpaa, T. (2002). Mul-
tiresolution gray-scale and rotation invariant texture
classification with local binary patterns. IEEE TPAMI,
24(7):971 –987.
Salas, S. and Hille, E. (1978). Calculus: One and Several
Variable. John Wiley and Sons, New York.
Xu, Y., Ji, H., and Ferm
¨
uller, C. (2009). Viewpoint invari-
ant texture description using fractal analysis. IJCV,
83(1):85–100.
Zhao, G., Ahonen, T., Matas, J., and Pietikainen, M. (2012).
Rotation-invariant image and video description with
local binary pattern features. Image Processing, IEEE
Transactions on, 21(4):1465 –1477.
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
502
