Reflection and Transmission Properties

of Light in Chiral Liquid-crystalline Photonic Structures

with Pitch Gradient and the Phenomenon of Nonreciprocity

H. Gharagulyan, H. Grigoryan, M. S. Rafayelyan, A. H. Gevorgyan and R. B. Alaverdyan

Yerevan State University, 1A.Manoogian, Yerevan, Republic of Armenia

Keywords: Chiral Photonic Crystal, Cholesteric Liquid Crystal, Nonreciprocity, Selective Reflection, Inhomogeneous

Pitch, Photonic Band Gap.

Abstract: In frame of this paper we have investigated reflection and transmission properties of light in chiral liquid-

crystalline photonic structures with inhomogeneous pitch. We have experimentally confirmed and

theoretically justified the existence of the phenomenon of nonreciprocity in the mentioned above systems.

The liquid-crystalline cells through the contact of two and more cholesteric liquid crystals with different

pitches and chiralities were prepared. The problem was solved by Berremann 4x4 matrix method. Our

results can be used in optical diodes, transistors and logical elements, as well as for expansion of Bragg’s

reflection range, namely in the systems as a broadband mirrors for circularly polarized light and in spatially

tunable liquid-crystalline lasers with a pitch gradient.

1 INTRODUCTION

During the last decade photonic crystals and various

photonic structures became one of the most

interesting objects of physics due to their unique

physical properties and their relevance for

development of new electro-optical and photonic

devices. The main peculiarity of PCs is the fact, that

they exhibit photonic band gaps (PBGs), namely

they prevent light propagation in certain frequency

ranges, which can be suitably tuned modifying their

structure (Joannopoulos et al. 1995); (Sakoda,

2001); (Johnson and Joannopoulos, 2002);

(Soukoulis, 2001). Chiral photonic crystals (CPCs),

namely cholesteric liquid crystals (ChLCs) are

classic examples of PCs. The main difference

between CPCs and usual photonic crystals lies in the

fact that the photonic band gap in CPCs exists only

for one polarization (in case of normal light

incidence) coinciding with the chiral medium helix

sign. ChLCs are particularly interesting one-

dimensional materials because of their spontaneous

self-assembly into periodic structures and the fact

that the photonic band gap can be tuned over a broad

range of frequencies. In terms of their optical

properties, a prominent feature of cholesterics is the

helical structure of their director axes. This helicity

gives rise to selective reflection and transmission of

circularly polarized light (Kolomzarov, et al., 1999);

(De Gennes and Prost, 1993). As we mentioned

above, the periodic structure of ChLCs leads to a

polarization sensitive photonic band gap. Its location

and width depend on the pitch p and the ordinary

) and extraordinary (n

) refractive indices of

cholesteric material. For ChLCs the reflection band

is defined by n

p<<n

p. Within the stop band only

circularly polarized light that has the same

handedness as the ChLC helix is selectively

reflected. Light polarized with the opposite

handedness and light with wavelengths outside the

stop band are both transmitted through the ChLC

cell. Maximum reflection efficiency at normal

incidence for ambient light is 50%. Therefore, ChLC

systems, that can reflect both right- and left-

circularly polarized light simultaneously, attract

scientists’ attention. For example, M. Mitov et al.

have obtained a way to exceed the 50% reflectance

limit (Mitov et al., 1999); (Dimitrios et al., 2006);

(Belalia et al., 2006). It is worthy to mention about

nonreciprocal photonic crystals, which are also of

special interest, the more so given that some new

mechanisms of nonreciprocity have been proposed

in recent years (Scalora et al., 1994); (Poladian,

1996). The importance of nonreciprocal photonic

crystals is related, in particular, to the possibility of

115

Gharagulyan H., Grigoryan H., S. Rafayelyan M., H. Gevorgyan A. and B. Alaverdyan R..

Reﬂection and Transmission Properties of Light in Chiral Liquid-crystalline Photonic Structures with Pitch Gradient and the Phenomenon of

Nonreciprocity.

DOI: 10.5220/0004340101150120

In Proceedings of the International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS-2013), pages 115-120

ISBN: 978-989-8565-44-0

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

creating optical diodes, unilateral reflectors etc.

Accordingly, a device transmitting light in one

direction and blocking its propagation in the reverse

direction (i.e., characterized by nonreciprocal

transmission) may be called a purely optical diode.

The importance of the creation and characterization

of optical devices (optical diodes, transistors, etc.)

analogous to electrical devices is related, in

particular, to the general tendency of using optical

signals instead of electrical. This trend is explained

by some advantages and extremely broad

possibilities offered by optical signals.

From applications point of view, photonic-

crystal-based devices should be important for

controlling of optical properties, because they do not

rely on the intrinsic properties of the constituent

materials. In particular, the properties of chiral

photonic crystals are dependent on the boundary

conditions, which can be engineered to suit a wide

variety of diverse applications. So, the optical

devices, constructed on the bases of chiral photonic

crystals result intelligent, multifunctional and

tunable optics, which possess such good traits, as

their compactness, small losses, high reliability and

compatibility with other devices. PCs, such as

cholesteric liquid crystals, artificial chiral-made

crystals etc., are used in switches, laser devices,

tunable filters, tunable optical chips, nonlinear

optical devices, colour displays, thermometers,

optical polarizers, as well as in thermal mapping and

for solar energy savings in building windows (Yeh

and Gu, 1999); (Wu and Yang, 2001); (Bahadur,

1991); (Foresi et al., 1997); (Mochizuki et al., 2000);

(Furumi and Sakka, 2006). Therefore, we can say

that ChLCs are widely used in basic research as well

as in commercial purposes.

2 DIFFUSION AND PITCH

GRADIENT PECULIARITIES

IN CPC STRUCTURES

The pitch change is caused as a result of the

molecular diffusion of the chiral components into

the ChLC as shown schematically in Fig.1. The

diffusion of molecules of LC in the depth direction

of the cell has been used to create a ChLC material

with a pitch gradient. A diffusion process between

compounds and therefore, a chirality gradient may

occur in a direction perpendicular to the plane of

films. Because of deformation the helical pitch

simply followed the changes in sample thickness.

At the beginning of the process the two original

parts can still be distinguished with their small and

large periodicity, but the interface is no longer

visible. Clearly the adjacent surfaces have merged

and diffusion has occurred. Finally, redistribution of

the chiral compound might allow the material to

adjust its local equilibrium pitch. The speed of CLCs

mixing by diffusion depends on four main

parameters: temperature, size (mass) of the diffusing

particles, viscosity of the structure and pressure. The

main characteristics of diffused layers are: surface

resistance or surface concentration of mixture, depth

of doped layer, as well as distribution of mixture’s

density in that layer. The concentration gradient in

the cell with the thickness d will be determined by

the following equation:



C = (C

-C

) / d,

(1)

where C

and C

are the concentrations

of diffusion

layers. For our sample the concentration gradient is

of the order about 2.8x10

-4

. So, the pitch

gradient is the consequence of the concentration

gradient. As we know diffusion process is

characterized by diffusion constant, which is the

quantitative characteristic of diffusion velocity. It

should be incorporated in the model for it to be

capable of predicting the pitch change phenomena

for given experimental conditions. It is defined by

medium’s properties. The diffusion process

throughout the sample allows the concentration

become uniform.

Figure 1: The model of ChLC pitch’s profile: a) at the

beginning of diffusion, b),c) in the middle of diffusion

process and d) at the end of diffusion.

The pitch profile is represented by the following

function:

(2)

where p

and p

are pitches of two cholesteric liquid

21 21

2( ) 3

() ( )( )

() 2

pp zz

pz p z z z



  



PHOTOPTICS2013-InternationalConferenceonPhotonics,OpticsandLaserTechnology

116

crystals.

Although the pitch gradient is formed along the

one direction, the liquid-crystalline material also

diffuses flowing on the transverse plane,

consequently the total thickness gradually

diminishes as the thermal diffusion process lasts

longer. As we know concentration increases when

pitch decreases. Helical twisting power (HTP) is

expressed by the pitch and concentration of ChLC:

HTP=1/(P*C), (3)

According to this equation ChLC pitch (reflection

band) is determined based on the concentration of

ChLC.

So, the ChLC film with a lateral pitch gradient

was prepared by thermally activated molecular

diffusion across the interface of two films with

disparate chiral concentrations. As we mentioned

above, in order to broaden the selective reflection

band we have changed the helix pitch. The pitch of

ChLCs can be varied by adding chiral dopants, by

adjusting temperature or by irradiating with light of

a specific wavelength, namely the helical pitch can

also be altered by UV irradiation of ChLC

containing light-sensitive molecules with variable

chirality controlling the pitch (Bodrovsky et al.,

2004). So, many external stimuli, such as pressure,

electric and magnetic fields, temperature and light

can be used to modify the pitch and /or average

refractive index of the CLCs (Munoz et al., 2001);

(Funamoto et al., 2005); (Furumi et al., 2004);

(Sackmann, 1971). The spectral position of the

reflection band can be tuned throughout the visible

spectrum: but since the typical birefringence of LCs

in the optical region is ∆n=n

-n

0,15-0,2, the

typical reflection bandwidth is limited to 50-100nm.

This fact is insufficient for some applications. By

introducing a pitch gradient in the helix (reflection

bandwidth with pitch gradient CLCs is defined by

∆= n

- n

) we show that reflection may occur

of a wavelength bandwidth greater 300nm.

Therefore the spectral position of reflection band can

be controlled in whole visible spectrum. A way to

make cholesteric films reflecting in a broad

wavelength band consists in associating different

cholesteric pitches in the same film. A controlled

helix pitch modulation in the in-plane direction of a

planarly aligned cholesteric liquid crystal cell by

using photopolymerizable cholesteric liquid-crystals

is demonstrated in the work of H.Yoshida and

Masanori Ozaki et al. (Hiroyuki et al., 2008). We

proposed an interesting method to produce film with

pitch gradient based on a thermal processing and we

studied the optical properties of this film with

respect to the time of processing. Let us recall that

our intention was to make double- and multiple-

pitched specimen. The type of linear pitch gradient

for achieving a broadband reflection was analysed

and the number of chiral pitches required for

establishing the stop-band was simulated. In this

case we have to know answers of two important

questions, namely: how to adjust the pitch and how

to keep it constant when the right value is reached?

It is worthy to mention, that we considered the

helical pitch variation profile uniformly along the

two directions. This idealization has been proven far

from being valid in practice: the cholesteric films

after the heating procedure showed both transversal

variations

and additionally, a disturbed longitudinal

profile.

3 EXPERIMENT

3.1 Sample Preparation

For investigation of spectral properties of ChLCs,

we have used right-handed pelargonium, left-handed

oleate and E7 nematic liquid crystals.

We have

prepared cholesteric liquid-crystalline cell through

the contact of two and more cholesteric liquid

crystals with different pitches and chiralities. The

inner surfaces of glass substrates were first coated

with thin polymide layer and then they were

uniaxially rubbed with special material. As a result,

the orientation of CLCs director was parallel to the

surfaces, which means that the helix axis was

perpendicular to the surfaces of the cell. The

substrates were coated with mixtures of different

pitches and chiralities. The mixture was drop-filled

into the empty sandwiched cell and it was sealed

with glue. After this procedure the cell showed the

pitch gradient produced by the mixing process.

Polyethylene films with a thickness of 15m were

used as the cell spacers and the distance between

them was 3,5mm.

3.2 Experimental Set-up

In order to investigate the transmission and

reflection spectra for unpolarized, linear and circular

polarized lights (at normal incidence) we have

assembled the experimental set-up, depicted in

Figure 2. In our experiment StellarNet spectrometer

with optical resolution of 0,75 nm was used.

ReflectionandTransmissionPropertiesofLightinChiralLiquid-crystallinePhotonicStructureswithPitchGradientand

thePhenomenonofNonreciprocity

117

Figure 2: Scheme of experimental set-up for investigation

of discussed system’s reflection and transmission spectra:

1. Tungsten-krypton lamp. 2. CLC cell, 3.

Microrefrigerator, 4. Controller of temperature, 5.Tester,

6. Spectrometer, 7. PC.

4 RESULTS AND DISCUSSION

It is worthy to mention about phenomenon of

nonreciprocity as well. It is in the centre of attention

of scientists, who are interested in the questions of

reflection and transmission.

Its experimental and theoretical justifications

were given for different liquid-crystalline systems

(Manipatruni et al., 2009); (Vardanyan and

Gevorgyan, 2005); (Miroshnichenko et al., 2010),

but in chiral photonic liquid-crystalline structures

with inhomogeneous pitch it isn’t justified yet, so

experimental and theoretical justifications of this

important phenomenon is considered one of the

basic questions of this paper. The meaning of

nonreciprocity phenomenon is that the optical

properties of liquid-crystalline system are different

from two different sides of the system, which means

that reflections of light from different sides of the

system are different. For our system the absorption

can be neglected, so for transmission coefficients the

phenomenon of nonreciprocity also takes place. The

phenomenon of nonreciprocity is widely used in

optical diodes, transistors, as well as in different

logical elements.

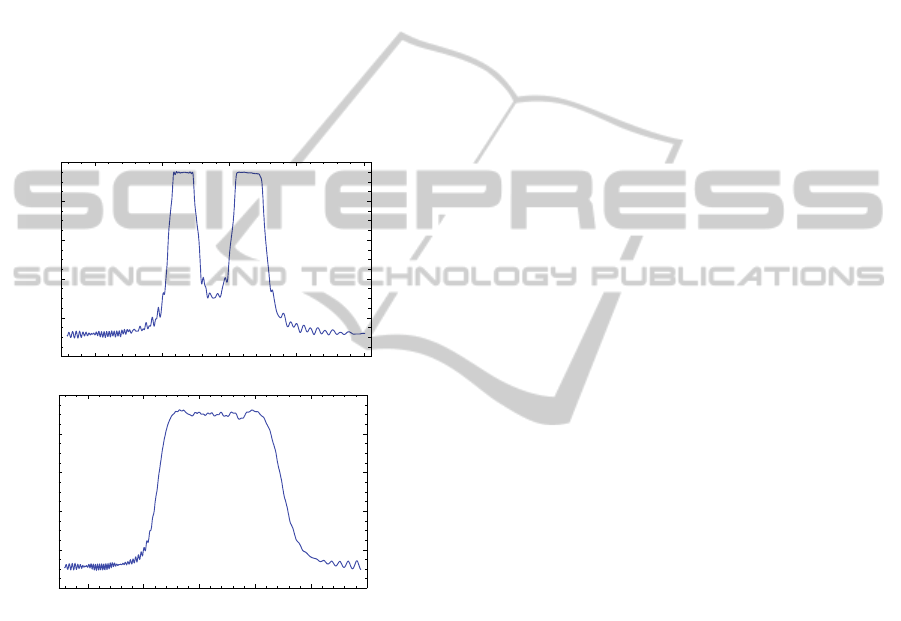
Figure 3 shows the reflection spectra of the cell

for different moments of diffusion process. At the

beginning of the diffusion process two peaks are

separated obviously, then two peaks come to close

each other. Finally, at the end of diffusion process

these two peaks almost can’t be distinguished.

5 METHOD OF ANALYSIS

In order to simulate our experimental results, we use

Berremann 4x4 matrix method. There are many

methods of solving the problem of electromagnetic

wave propagation through a 1D anisotropic PC layer

Figure 3: Reflection spectra of the cell for different

moments of diffusion process: a )at the beginning of

diffusion, b ) in the middle of diffusion process and c)at

the end of diffusion.

but it seems that the most applicable one has

recently become the Berremann’s method

(Berreman, 1972). According to Berreman’s

method, the Maxwell’s equations will presented as

follows:















, (4)

where

,,,

xyy x

EHE H















is the field

generalized vector p



is the well-known

PHOTOPTICS2013-InternationalConferenceonPhotonics,OpticsandLaserTechnology

118

Berremann’s 4x4matrix.

The solution of equation (4) can be expressed by

the characteristic matrix

  

2212

,zPzz z





(5)

For the multilayer structures

is defined by the

following product:





















1311

ˆˆ ˆ ˆ ˆ ˆ

...

PP P P P P



 

(6)

In Figure 4 simulation results are presented,

namely the reflection spectra of the cell are

calculated at the beginning and at the end of

diffusion process.

400 500 600 700 800

avelength

n Nanometer

ectance



400

700 800 900

Wavelength

n Nanometer

ectance



Figure 4: Reflection dependences on wavelength of the

cell for different moments of diffusion process.

As it is obvious from the graphs, the simulation

results agree with experiment. Let us not that the

absorption of the ChLC medium is neglected.

6 CONCLUSIONS

In summary, we theoretically designed the ChLC

cell with two and more cholesterics of different

pitches and chiralities, as well as experimentally

demonstrated the peculiarities of this system. Thanks

to the diffusion process, we created a gradient in the

pitch of the helix. The pitch gradient was stable for

few months. So, as a result of the sensitivity of the

helical pitch we create a new material. We also

showed that the bandwidth of cholesteric reflection

was broaden. Our studies provide important insights

into self-assembled photonic investigations to go

into details about the diffusion mechanism between

the individual films inside the cell. The comparison

of experimental results with the theoretical

predictions confirms the validity of the approach.

Work is in progress aiming to improve our sistem’s

nonreciprocity.

ACKNOWLEDGEMENTS

This work was supported by Grant 11-1c194 of State

Committee of Science of Republic of Armenia.

REFERENCES

Joannopoulos, J., Meade, R., and Winn, J., 1995.

Photonic Crystals, Princeton Univ.

Sakoda, K., 2001. Optical properties of Photonic crystals,

Berlin: Springer.

Johnson, S., G., and Joannopoulos, J., 2002. Photonic

Crystals: The Road from Theory to Practice, Boston:

Kluwer.

Soukoulis, C., M., (Ed), 2002. Photonic Crystals and

Light Localization in the 21st Century. NATO Science

Series C: Vol.563. 616 p.

Kolomzarov, Yu., Kozachenko, A., Lev, B., Nazarenko,

V., and Sorokin, V., 1999. Some peculiarities of

angular selective reflection of cholesteric liquid

crystals in an electric field, Jpn. J. Appl. Phys., 814-

817, Part1, No2A, February.

De Gennes, P., G., Prost, J., 1993. The Physics of Liquid

Crystals, Clarendon Press, Oxford, 271-280.

Mitov, M., Boudet, A., and Sopena, A., 1999. From

selective to wind-band light reflection: a simple

thermal diffusion in a glassy cholesteric liquid crystal,

Eur.Phys.J.B8, 327-330.

Dimitrios C., Emmanouil E., Kriezis, Michel Mitov,

Corinne Binet, 2006. Theoretical and experimental

optical studies of cholesteric liquid crystal films with

thermally induced pitch gradient, Physical Review E

73, 061701

Belalia, M., Mitov, M., Bourgeratte, C., Krallafa, A.,

Belhakem M., and Bormann,D., 2006. Cholesteric

liquid crystals with a helical pitch gradient: Spatial

distribution of the concentration of chiral groups by

Raman mapping in relation with the optical response

and the microstructure, Phys. Rev. E 74, 051704.

Scalora, M., J., P., Dowling, C., M., Bowden, and M., J.,

Bloemer, 1994, The Photonic Band Edge Optical

Diode, J.Appl.Phys. 76, 2023.

Poladian, L.,1996, Resonance mode expansions and exact

ReflectionandTransmissionPropertiesofLightinChiralLiquid-crystallinePhotonicStructureswithPitchGradientand

thePhenomenonofNonreciprocity

119

solutions for nonuniform gratings, Phys. Rev. E 54,

2963

Yeh, P., and Gu, C., 1999. Optics of Liquid Crystal

Displays, New York: Wiley.

Wu, S., T., and Yang, D., K., 2001. Reflective Liquid

Crystal Displays (New York: Wiley).

Bahadur, B., 1991. Liquid Crystals: Applications and

Uses, edited by (World scientific, Singapore).

Foresi, J., S., Villeneuve, P.,R., Ferrera, J., Thoen, E., R.,

Steinmeyer, G., Fan, S., Joannopoulos, J., D.,

Kimerling, L., C., Smith, H., I., and Ippen, E.,P., 1997.

Photonic-bandgap microcavities in optical

waveguides, Nature (London) 390, 143.

Mochizuki, H., Hasui, T., Shiono, T., Ikeda, T., Adachi,

C., Taniguchi, Y., and Shirota, Y., 2000. Emission

Behavior of Molecularly-Doped Electroluminescent

Device Using Liquid-Crystalline Matrix, Appl. Phys.

Lett. 77, 1587.

Furumi, S., and Sakka,Y., 2006. Adv. Mater. (Weinheim

Ger)18, 775.

Bodrovsky, A., Boiko, N., Shibaev, V., Wendorff, J.,

2004. Photoinduced textural and optical changes in a

cholesteric copolymer with azobeneze-containing side

groups, Liquid Crystals 31, 351-359.

Munoz, A., Palffy-Muhoray, F., P., and Taheri, B., 2001

Ultraviolet lasing in cholesteric liquid crystals, Opt.

Lett. 26, 804-806.

Funamoto, K., Ozaki, M., and Yoshino, K., 2005.

Discontinuous Shift of Lasing Wavelength with

Temperature in Cholesteric Liquid Crystal,

Jpn.J.Appl.Phys.42, L1523-L1525.

Furumi, S., Yokoyama, S., Otomo, A., and Mashiko, S.,

2004.Phototunable photonic bandgap in a chiral

liquid crystal laser device, Appl.Phys.Lett.84, 2491-

2493.

Sackmann, E., 1971. Photochemically induced reversible

color changes in cholesteric liquid crystal,

J.Am.Chem. Soc. 93, 7088-7090.

Hiroyuki, Yoshida, Yusuke, Miura, Kazuki, Tokuoka,

Satoshi Suzuki, Akihiko Fujii and Masanori Ozaki,

2008. In-plane pitch control of cholesteric liquid

crystals by formation of artificial domains via

patterned photopolymerization, 10 November , Vol.

16, No. 23, OPTICS EXPRESS 19033.

Manipatruni, S., Robinson, J.,T., and Lipson, M. 2009.

Optical Nonreciprocity in Optomechanical Structures,

Phys. Rev. Lett. 102, 213903.

Vardanyan, G., A., and Gevorgyan, A., A., 2005. Wave

nonreciprocity in inhomogeneous gyrotropic media

and multilayer systems: I. Inhomogeneous gyrotropic

media, Optics and Spectroscopy Volume 99, Number

Miroshnichenko, A., E., Brasellet E., and Kishvar, Y., S.,

2010. Reversible optical nonreciprocity in periodic

structures with Liquid crystals, Applied Physics

Letters 96,063302.

Berreman. J., D., W., 1972. Opt. Soc. Am., 62, 502-510.

PHOTOPTICS2013-InternationalConferenceonPhotonics,OpticsandLaserTechnology

120