
Job Order Assignment at Optimal Costs in Railway Maintenance
Franziska Heinicke
1
, Axel Simroth
1
, Roberto Tadei
2
and Mauro M. Baldi
2
1
Fraunhofer Institute for Transportation and Infrastructure Systems IVI, Dresden, Germany
2
DAUIN, Politecnico di Torino, Turin, Italy
Keywords:
Railway Maintenance Planning, Job Order Scheduling, Operations Research.
Abstract:
Tamping is an important part of railway maintenance. Well tamped ballast reduces track irregularities and
increases travel safety and comfort. But if the ballast is in a bad condition, the train speed must be restricted,
which leads to delays and penalty costs for the operator. In this paper a novel model for the tamping scheduling
problem in a short-term planning horizon is presented. In contrast to other railway maintenance scheduling
problems the penalty costs caused by deferring tamping activities are considered in the scheduling process
beside the travel costs. Three greedy heuristics are presented and compared in different benchmarks. An
outlook discusses issues of interest for further research.
1 INTRODUCTION
Tamping is an important part of railway maintenance.
Well tamped ballast reduces track irregularities and
increases travel safety and comfort. But if the bal-
last is in a bad condition, the train speed must be re-
stricted, which leads to delays and penalty costs for
the operator. By scheduling the tamping works these
penalty costs should be minimised together with in-
curred travel costs.
Within the ACEM-Rail project of the Europeans
Seventh Framework Programme a novel solution ap-
proach for the tamping scheduling problem will be
developed. In this paper the model is presented, first
solution approaches are shown and a look out of the
further research is given.
There are different papers dealing with railway
maintenance scheduling.
Higgins and Ferreira (1999) develop an integer
programming model to reduce train delays caused by
maintenance activities. The problem is solved with a
Tabu-Search heuristic.
Budai develops solution approaches for the pre-
ventive maintenance scheduling problem (PMSP)
(Budai et al., 2004, 2009). Aim of the PMSP is
to minimize track possession costs caused by sched-
uled routine activities and projects. For this purpose
they combine as much tasks as possible. The prob-
lem is formulated as integer programming model and
solved with heuristics and evolutionary computation
approaches.
In (Miwa, 2002; Oyama and Miwa, 2006) an in-
teger programming model for optimally scheduling
a multiple tie tamper is shown. The objective is to
maximize the improvement of track condition under
bounded maintenance costs. The resulting schedule
defines for each 10 day term where to locate the tam-
per and which lots to be maintained.
Gorman and Kanet (2010) and Peng et al. (2011)
present a time-space network to schedule larger
projects to maintenance crews and execution weeks.
They consider the specification of the crews (not ev-
ery crew could execute all tasks), time windows (ear-
liest start and latest resolving time of a project), travel
costs, and cross-job constraints (precedence, non-
concurrent, simultaneity).
An integer programming model to minimize the
tamping effort is presented by Vale et al. (2012). The
optimal time-allocation to 90 day terms is searched,
such that the track quality keeps a given level. They
take into account four aspects of tamping: the time
dependent deterioration process, the track layout, the
imperfect track quality after maintenance and the
track quality limits that depend on the maximal per-
missible train speed.
In (Quiroga and Schnieder, 2010) a heuristic ap-
proach for the tamping scheduling problem is pre-
sented. Aim is to find a set of N interventions, one
per night, which maximise a defined objective func-
tion, e.g. the expected track condition one year later.
An intervention is defined by a start depot, the tamp-
ing works, and an end depot.
156
Heinicke F., Simroth A., Tadei R. and M. Baldi M. (2013).
Job Order Assignment at Optimal Costs in Railway Maintenance.
In Proceedings of the 2nd International Conference on Operations Research and Enterprise Systems, pages 304-309
DOI: 10.5220/0004343603040309
Copyright
c
SciTePress

The model presented here is different. On the one
hand the planning horizon is short-termed – a few
weeks or months – and the schedule defines explicitly
the execution times of small tamping works. On the
other hand so-called daily costs – penalty costs for re-
strictions in railway services caused by the untamped
track – are considered in the decision process and will
be minimised together with the costs for traveling be-
tween the tamping works.
The paper is organised as follows: In section 2
the short-term tamping scheduling problem is defined.
Three Greedy Heuristics are presented and compared
in section 3. Issues of interest for further research
– extensions of the model and concepts for general
solution approaches – are presented in section 4.
2 PROBLEM FORMULATION
The short-term tamping scheduling problem is de-
fined as follows. Given a set of jobs that are defined
by
• working duration
• daily costs
• location in the network.
There is a single tamping machine operating at the
network and resolving jobs one after the other. The
jobs are executed during the night in an eight hour
working shift. For each job the execution time has to
be assigned in order to minimize maintenance costs.
At the time at which the plan is calculated the tamping
machine is located in section A and when all jobs are
resolved, the machine will be parked at section B (the
depot).
Each job refers to a small section of the track with
a short working duration (about half an hour) such
that the planning flexibility is high, but the number
of jobs is not too large. The daily costs are caused
by traffic restrictions (like speed limitations) result-
ing from a bad track condition. They have to be paid
for every day from the beginning until the job is re-
solved. If the track condition is still acceptable, the
daily costs of the corresponding job are zero. Be-
cause of the short planning horizon (a few weeks or
months) the time-dependence of track condition and
thus the time-dependence of the daily costs is not con-
sidered. The costs and time for traveling between jobs
are calculated based on the locations in the network.
The travel times contain 15 minutes for changeover
between travel and working mode. Between jobs of
consecutive track sections the time and costs for trav-
elling are zero. In practice they are executed within
one larger working step and without traveling. If the
work will be continued in the next night at the same
location the machine stays nearby over day. Thus no
costs and time for travelling to a machine depot are
incurred. If the work starts next night on another loca-
tion the machine travels over day to the new location.
The material costs, machine rent and the employee’s
wages are not included in the model, because they are
fixed and must be paid no matter if the job is executed
today or in a week. Thus only the travel costs and the
daily costs must be considered in an objective func-
tion.
The problem could be described as an integer pro-
gramming model. Given a set of jobs J, |J| = n. Let
for each job j ∈ J
• d( j) the working duration
• c
d
( j) the daily costs
• c
t
( j, k) the travel costs between the jobs j, k ∈ J
• t
t
( j, k) the travel time between the jobs j, k ∈ J
Aim of the optimisation is to assign an execution time
t
e
( j), such that the maintenance costs are minimal.
For the start point A and the end point B two ar-
tificial jobs j
A
and j
B
, are defined and J
AB
:= J ∪
{ j
A
, j
B
}. For both working duration and daily costs
are zero. The travel costs and time are calculated from
the locations in the network.
The execution time t
e
= (t
e
1
,t
e
2
) consists of two
components: the execution day t
e
1
≥ 1 and the ex-
ecution minute t
e
2
∈ [T
1
, T
2
]. The execution minute
is restricted by the working shift, that starts at
T
1
b= 10:00 p.m. and ends at T
2
b= 6:00 a.m. For j
A
the execution time is set to t
e
( j
A
) = t
start
, which is the
time at which the plan is calculated.
The problem can be formulated as follows:
min z =
∑
j∈J
AB
∑
k∈J
AB
c
t
( j, k)· x( j, k)
+
∑
j∈J
AB
t
e
1
( j) · c
d
( j)
(1)
with
t
e
( j
A
) = t
start
t
e
( j
B
) = (∞, 0)
(2)
x( j,k) =
1 , if @l ∈ J
AB
: t
e
( j) < t
e
(l) < t
e
(k)
0 , else
(3)
subject to
t
e
(k) ≥ t
e
( j) + d( j)+t
t
( j, k)
∀ j,k ∈ J
AB
: x( j, k) = 1
(4)
t
e
1
( j) ≥ 1
t
e
2
( j) ≥ T
1
t
e
2
( j) + d( j) ≤ T
2
∀ j ∈ J (5)
With the objective function (1) the maintenance costs,
i.e. the sum of the costs for traveling between the jobs
and the daily costs, are minimised.
JobOrderAssignmentatOptimalCostsinRailwayMaintenance
157

The maintenance machine starts at t
start
in track
section A and will be parked at track section B, when
all jobs are resolved. The execution times of the re-
spective jobs j
A
and j
B
are defined in equation (2).
Binary variables x( j, k) state whether two jobs are re-
solved directly one after the other and thus if travel
costs occur or not (see (3)). A distinction whether two
jobs are on consecutive track sections is not necessary
because the travel time and travel costs between jobs
of consecutive track sections are zero. By constraint
(4) and (5) it is ensured that the scheduled execution
times are feasible.
The problem can be reduced to a job order
assignment problem. Instead of determining the
explicit execution time for each job, the order
J
O
= ( j
1
, j
2
, ..., j
n
) to resolve the jobs j
i
∈ J has to be
specified. Then for the order ( j
A
, j
1
, j
2
, ..., j
n
, j
B
) the
minimal feasible execution times are calculated based
on the equations (2)–(5).
The tamping scheduling problem is similar to the
travelling salesman problem. Instead of visiting cities
jobs are resolved. The main difference is the objective
function. Not only the costs for travelling between
the jobs are minimised, but also the daily costs, that
depends on the execution day, have an influence on
the solution quality.
Also, the problem shows resemblance to the rural
postmen problem (a variant of the Chinese postman
problem). There a shortest closed path is searched in
a graph that pass through an edge subset. The graph is
given by the track network and the edges are the track
sections with a job. Again, the objective function dif-
fers because of the daily costs.
Both problems are NP-hard, thus the tamping
scheduling problem is NP-hard, too.
3 GREEDY HEURISTICS
Dependent on the ratio between daily and travel costs
different solution approaches are reasonable. For ex-
ample, if the daily costs of all jobs are zero or very
small, a heuristic that minimises travel costs leads
to good results. Contrariwise, if the travel costs are
much lower than the daily costs it is important to pre-
fer jobs with high daily costs, even if this causes de-
tours. Three different greedy heuristics are presented,
which show good results in different benchmarks. All
greedy heuristics follows the same procedure, see Al-
gorithm 1.
Starting with an arbitrary job k ∈ J the job order
J
O
(k) = (k) is built up step-by-step: A job j ∈ J that
is not contained in the job order so far is selected by a
heuristic-specific selection criterion and added to the
Algorithm 1: General Greedy Heuristic procedure.
J
∗
O
:= ();
z
∗
:= ∞;
for k ∈ J do
J
O
(k) := (k);
repeat
select j ∈ J \ J
O
(k);
append j at the end of J
O
(k);
until J \ J
O
(k) ==
/
0;
determine execution times;
calculate maintenance costs z(J
O
(k));
if z(J
O
(k)) < z
∗
then
z
∗
:= z(J
O
(k));
J
∗
O
:= J
O
(k);
end
end
return J
∗
O
end of J
O
(k). This step is repeated until all jobs are
contained of the job order. Then j
A
and j
B
are added
to complete the order, the execution times are deter-
mined based on the equations (2)–(5), and the costs of
the job order are calculated.
To improve the solution quality a job order J
O
(k)
is generated for each job k ∈ J and the best of these
job orders is selected.
In the following the three selection criterions are
presented. In section 3.4 a comparison of the three
heuristics is made.
3.1 Nearest Job
At each step of Algorithm 1 the nearest uncontained
job, thus the one with the lowest travel costs to the
last job in the order, is selected and added. If there
are two or more jobs with the same distance, then the
job with the highest daily costs is chosen.
With the Nearest Job Greedy Heuristic the travel
costs are kept small, but the daily costs play a minor
role in the decision process.
3.2 Most Expensive Job
At each step of Algorithm 1 the most expensive job
is selected and added to the job order. If there is
more than one job with the same costs, the nearest
of them is selected. In our model it is assumed that
the daily costs of consecutive track sections typically
fluctuate. Then these selection criterion leads to high
fragmented solutions. Often the machine travels to re-
solve only a single job, and then travels to a different
track section for the next job. To avoid such a frag-
mentation of the job order, direct neighboured jobs
ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems
158
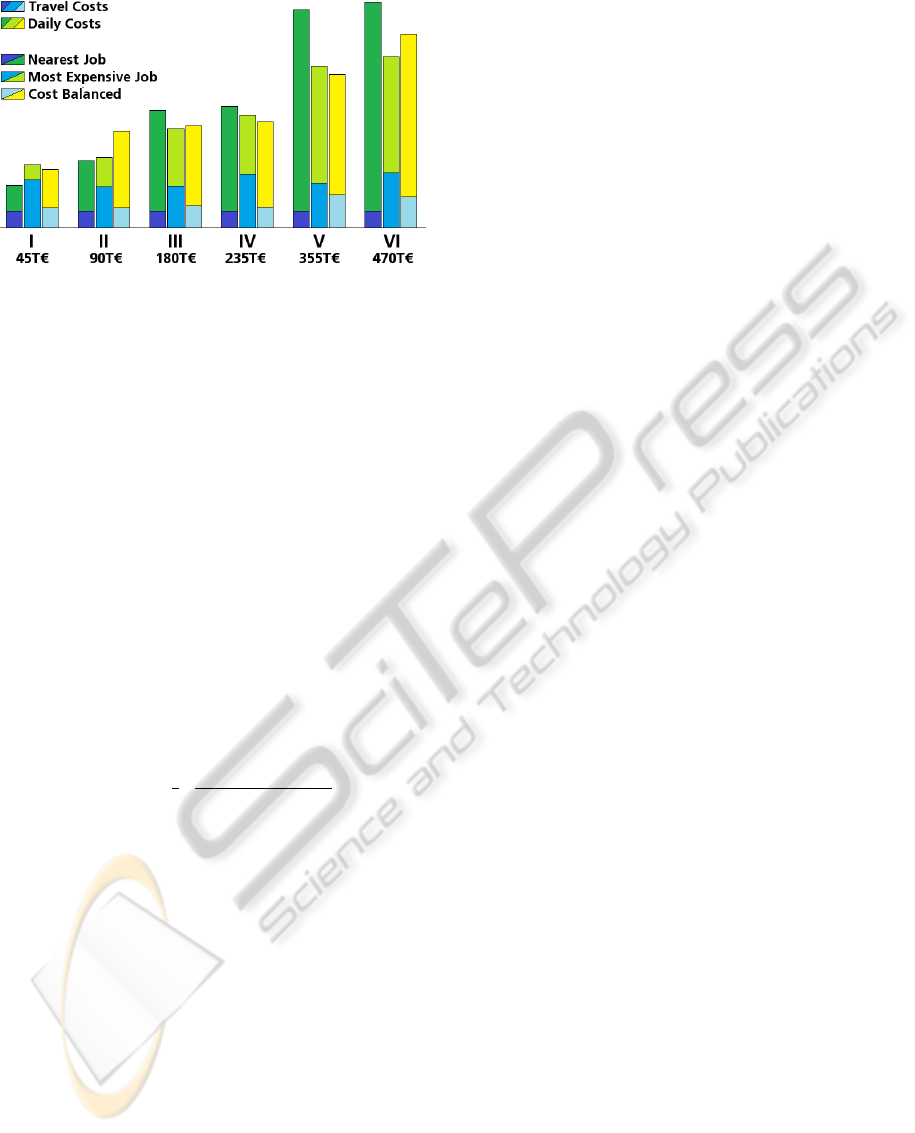
Figure 1: Results of the three greedy heuristics in six bench-
marks.
are preferred. That means if there is a job that could
be reached without traveling and has daily costs in the
same cost range as the most expensive one, this job is
added instead of the most expensive job.
The Most Expensive Job Greedy Heuristic usually
results in a job order where the jobs with non-zero
daily costs are always added first. The jobs with-
out daily costs are added similar to the Nearest Job
Greedy Heuristic.
3.3 Cost Balanced
Here, both costs are considered by defining a com-
bined cost measure. With this the travel costs and a
very rough estimation for the savings in daily costs
are summed. For each job that is not contained in the
job order the cost measure is calculated by
m
c
( j) = c
t
( j
l
, j)− α · c
d
( j)
with α =
1
2
·
# unresolved jobs
# jobs resolved per day
(6)
where j
l
is the last job in the current order and α is
an estimation on the number of days the job will stay
unresolved until now. If one of the direct neighboured
jobs has daily costs in the same cost range as j
l
, this
job is chosen. Again, this avoids a fragmentation of
the solution like in the Most Expensive Job Greedy
Heuristic. Otherwise the job with the minimal cost
measure m
c
is selected.
With the Cost Balanced Greedy Heuristic both
kinds of costs are considered in the decision process.
3.4 Comparison
The three greedy heuristics are tested in different
benchmarks. In Figure 1 the results of the heuristics
are compared in six benchmarks (I–VI). All bench-
marks are built up of 1415 jobs on a network with
more than 1400 km of track. 353 of them are af-
flicted with daily costs ranging from 45,000 e per day
(benchmark I) up to 470,000 e in benchmark VI. The
jobs with non-zero daily costs are located in the cen-
tre of the track network. The travel costs are 1000 e
per kilometre. To resolve all jobs at least 184,500 e
have to be paid for travelling.
In the bar graphs the travel costs (lower part) and
the daily costs (upper part) are stacked. The left bar
shows the results of the Nearest Job Greedy Heuristic
(short NJ), in the middle bar the results of the Most
Expensive Job Greedy Heuristic (MEJ) are plotted,
and the right bars represents the results of the Cost
Balanced Greedy Heuristic (CB).
Due to the fact that the benchmarks only differ in
the daily costs, NJ always generates the same solu-
tion for a certain first job k ∈ J. In each benchmark
the same job order J
∗
O
is selected and thus always the
same travel costs occur. Only the daily costs differ
due to the different daily costs in the benchmarks.
Benchmark I – III and V are very similar: in
benchmark II the daily costs of benchmark I are dou-
bled, in benchmark III they are fourfold and in bench-
mark V the costs are eightfold.
In benchmark I and II the share of the daily costs is
low. NJ starts with the most expensive track sections
and resolves the other jobs without much traveling.
This leads to a plan with low travel and daily costs.
The heuristic CB leads to a solution with higher daily
and higher travel costs than NJ. One reason is that
the daily costs are underestimated and that the jobs
with non-zero daily costs are resolved as long as the
detour is short. So the travel costs are higher as with
NJ and there are no savings in daily costs. By MEJ the
jobs afflicted with daily costs are resolved first. This
leads to long detours and to an increase in travel costs,
which cannot be compensated by the savings in daily
costs.
In benchmark III NJ obtains the same plan as in
benchmark I and II, but the daily costs are much
higher, so the expensive jobs should be preferred.
Also with CB the daily costs are underestimated and
thus they have a high share in the costs of the job or-
der. By MEJ the most expensive jobs are resolved first
with long detours, but this time this can be is compen-
sated by the savings in daily costs.
In benchmark V the daily costs have a huge share in
the overall costs. The cost measure of jobs with non-
zero daily costs is low and these jobs will be resolved
first. Because of the consideration of travel costs in
the decision process CB leads to better results than
MEJ. The detours are shorter, but the jobs afflicted
with daily costs are nevertheless resolved first.
In the benchmark IV and VI the daily costs differ
even more. There are 115 jobs with high daily costs
in the centre of the network on a line. The other jobs
JobOrderAssignmentatOptimalCostsinRailwayMaintenance
159

have only small daily costs and are located around.
Resolving the jobs with small daily costs first leads
to long detours, which could be compensated by the
savings in daily costs only in benchmark VI. In bench-
mark IV the small daily costs are low enough, so that
long detours to resolve them are not necessary. There-
with CB obtains the best result.
The heuristics have also been tested in further
benchmarks, with different jobs on the network and
different assignments of daily costs to jobs. We no-
ticed that it is hard to predict which heuristic obtains
the best result. But some statements are possible:
• If the daily costs have a small share in the mainte-
nance costs, then NJ and CB obtains good results,
because they minimise the travel costs.
• If the daily costs are high and scattered over the
track network, then CB obtains the best results.
MEJ resolves the expensive jobs more ordered by
daily costs and thus travels crisscross through the
network, where CB resolves the expensive jobs
first, too, but ordered by location. The resulting
savings in travel costs compensate the small in-
crement in daily costs.
• If the daily costs are medium or high and clus-
tered, then MEJ obtains good results, because of
the lower travel effort. Within CB the daily costs
often are underestimated in this type of bench-
marks, which leads to worse results.
4 ISSUES OF INTEREST FOR
FURTHER RESEARCH
The model presented in section 2 will be extended by
some additional points, see section 4.1.
In the further research solution approaches will
be developed that are suitable for arbitrary ratios be-
tween daily and travel costs, and that can handle the
additional restrictions from the model extension. The
metaheuristic Simulated Annealing (section 4.2) and
a multilevel solution approach (section 4.3) will be
implemented and compared in terms of solution qual-
ity and computation time in different benchmarks.
4.1 Model Extension
(1) K machines are available to resolve the jobs. So
K disjunctive job orders have to be defined and non-
simultaneous restrictions must be considered (e.g. a
minimal distance must be kept between two tamping
machines).
(2) Maintenance is not always possible. Due to night
trains, freight traffic, and other maintenance activities
the possible execution times of a certain job will be
restricted. In the model time windows will be defined
for each job when maintenance is possible. If the time
window ends before the maintenance works are fin-
ished, the crew must leave the track and wait for the
next time window.
(3) Consideration of depots. In some railway net-
works it is not possible or not common that the main-
tenance machine stays close to the track over the day.
There the machine stays in a depot. Then not only the
jobs are scheduled, but also the best depot to stay over
day must be determined and additional travel costs
must be considered.
4.2 Simulated Annealing
The basic idea of Simulated Annealing comes from
annealing processes in metallurgy. After heating the
metal the atoms are inordinated. Through the slow
cooling process they have enough time to order them-
self and to form crystals. This leads to a low-energy
state.
The algorithm starts in the “hot stage” with a
initial solution s and a high temperature T . Then
the solution ˜s is created by modifying s. Depen-
dent on the temperature T , the probability P(s, ˜s,T ) =
min{1, e
z(s)−z(˜s)
T
} to accept ˜s is calculated. If ˜s is ac-
cepted, then s := ˜s. After that the temperature is
cooled. This step – modify solution s, accept the mod-
ified ˜s with probability P(s, ˜s, T ), cool T – is repeated
until a given minimal temperature is reached. Then
the best solution is returned.
The challenge in the design of a proper Simulated
Annealing approach for an optimisation problem is
the definition of a modification heuristic to get the so-
lution ˜s and of a cooling schedule for T . For out tamp-
ing scheduling problem at first methods from solving
the TSP are implemented. The SA starts with a ran-
dom job order. The solution is modified by a 2-opt
method Meer (2007): Two indices 0 ≤ i < j ≤ n + 1
are chosen randomly and the suborder between i and
j is inverted. The temperature T is cooled exponen-
tially. This leads to a fast improvement of the solution
quality, but at the end the solution remains a bit frag-
mented. To smooth the solution a post-optimisation
method will be developed. With this, irregularities –
like jumping over a few jobs and resolve them later –
will be removed without losing the solution structure.
4.3 Multilevel Branch and Bound
Multilevel solution approaches are common methods
in graph partitioning Karypis and Kumar (1996) and
VLSI-design Cong et al. (2005). A multilevel solution
approach consist of three steps:
ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems
160

1. Coarsening: merge objects to super objects
2. Solving: find a (nearly) optimal solution for the
super object problem
3. Refinement: transfer the solution back to the orig-
inal problem and post-optimise
Step 1 is repeated until the number of super objects
fall below a given threshold. Then the small prob-
lem is solved (step 2). Step 3 is executed as often
as step 1. On each level the post-optimisation step
can be used to improve the solution quality. For the
tamping scheduling problem a multilevel Branch and
Bound method seems to be a promising approach. In
practise, mostly some consecutive jobs are resolved
in one working step without travelling. Thus jobs of
consecutive track sections can be merged to one su-
per job. Therewith the problem size is decreased and
the application of exact methods, like a Branch and
Bound approach, is possible. The solution obtained is
transferred back to the original problem. In the post-
optimisation step the super job structure will be bro-
ken by rearranging single jobs in order to improve the
solution.
ACKNOWLEDGEMENTS
We acknowledge the financial support from the Eu-
ropean Communitys Seventh Framework Programme
under Grant Agreement no. 265954, ACEM-Rail
project. The EC is not liable for the use that can be
made of the information contained herein.
REFERENCES
Budai, G., Dekker, R., and Kaymak, U. (2009). Genetic
and memetic algorithms for scheduling railway mainte-
nance activities. Technical report, Econometric Institute,
Erasmus University Rotterdam.
Budai, G., Huisman, D., and Dekker, R. (2004). Schedul-
ing preventive railway maintenance activities. Technical
report, Econometric Institute, Erasmus University Rot-
terdam.
Cong, J., Fang, J., Xie, M., and Zhang, Y. (2005). Mars-a
multilevel full-chip gridless routing system. Computer-
Aided Design of Integrated Circuits and Systems, IEEE
Transactions on, 24(3):382 – 394.
Gorman, M. F. and Kanet, J. J. (2010). Formulation and
solution approaches to the rail maintenance production
gang scheduling problem. Journal of Transportation En-
gineering, 136:701–708.
Higgins, A. and Ferreira, L. (1999). Scheduling rail track
maintenance to minimise overall delays. In Proceedings
of the 14th International Symposium on Transportation
and Traffic Theory.
Karypis, G. and Kumar, V. (1996). Parallel multilevel graph
partitioning. In Parallel Processing Symposium, 1996.,
Proceedings of IPPS ’96, The 10th International, pages
314 –319.
Meer, K. (2007). Simulated annealing versus metropo-
lis for a TSP instance. Information Processing Letters,
104(6):216 – 219.
Miwa, M. (2002). Mathematical programming model anal-
ysis for the optimal track maintenance schedule. QR of
RTRI, 43:131–136.
Oyama, T. and Miwa, M. (2006). Mathematical modeling
analyses for obtaining an optimal railway track mainte-
nance schedule. Japan J. Indust. Appl. Math., 23:207224.
Peng, F., Kand, S., Li, X., and Ouyang, Y. (2011). A heuris-
tic approach to the railroad track maintenance scheduling
problem. Computer-Aided Civil and Infrastructure Engi-
neering, 26:129–145.
Quiroga, L. M. and Schnieder, E. (2010). A heuristic ap-
proach to railway track maintenance scheduling. WIT
Transactions on The Build Environment, 114:687–699.
Vale, C., Ribeiro, I. M., and Calc¸ada, R. (2012). Integer
programming to optimize tamping in railway track as
preventive maintenance. Journal of Transportation En-
gineering, 138:123–131.
JobOrderAssignmentatOptimalCostsinRailwayMaintenance
161
