
3D Face Pose Tracking from Monocular Camera via Sparse
Representation of Synthesized Faces
Ngoc-Trung Tran
1
, Jacques Feldmar
2
, Maurice Charbit
2
Dijana Petrovska-Delacr
´
etaz
1
and G
´
erard Chollet
2
1
Telecom Sudparis, Paris, France
2
Telecom ParisTech, Paris, France
Keywords:
Pose Tracking, Pose Estimation, Sparse Representation.
Abstract:
This paper presents a new method to track head pose efficiently from monocular camera via sparse represen-
tation of synthesized faces. In our framework, the appearance model is trained using a database of synthesized
face generated from the first video frame. The pose estimation is based on the similarity distance between
the observations of landmarks and their reconstructions. The reconstruction is the texture extracted around
the landmark, represented as a sparse linear combination of positive training samples after solving `
1
-norm
problem. The approach finds the position of new landmarks and face pose by minimizing an energy function
as the sum of these distances while simultaneously constraining the shape by a 3D face. Our framework gives
encouraging pose estimation results on the Boston University Face Tracking (BUFT) dataset.
1 INTRODUCTION
Head pose tracking is an important issue and has
received much attention in the last decade because
of the multiple applications involved such as video
surveillance, human computer interface, biometrics,
etc. The difficulties come from a number of factors
such as projection, multi-source lighting as well as bi-
ological appearance variations, facial expressions and
occlusion with accessories, e.g. glasses, hats... and
especially the self-occlusion of the face appearance
depending on head pose.
Since the pioneer work of (Cootes and Taylor,
1992; Cootes et al., 1998), it is well-known nowa-
days that the Active Shape Model (ASM) and Active
Appearance Model (AAM) provided an efficient ap-
proach for face pose estimation and tracking frontal
or near-frontal faces. Then some extensions (Xiao
et al., 2004; Gross et al., 2006) have been devel-
oped. More recently, some works tackled local ap-
pearances changes by exhaustive local search around
landmarks constrained by a 3D shape model, called
deformable model fitting. This method can track sin-
gle non-frontal face of large Pan angle well in well-
controlled environment (Saragih et al., 2011). How-
ever, it requires a lot of training data to learn 3d shape
and local appearance distributions. It is a limitation
which makes them costly in unconstrained environ-
ments.
Another approach to track faces and estimate pose
uses 3d rigid models such as semi-spherical or semi-
cylindrical (Cascia et al., 2000; Xiao et al., 2003),
ellipsoid (Morency et al., 2008) or mesh (Vacchetti
et al., 2004). These methods do not need a lot training
data and can estimate three rotations. However, these
models assume constant distances between points and
only rigid transformation can be applied on. This hy-
pothesis is efficient when the face is far from cam-
era and the image resolution is low. The low num-
ber of degree of freedom of these models facilitates
the alignment process since there is not many param-
eters to optimize. The bias introduced by these strong
constraints on the model can be restrictive particularly
when the morphology of facial expressions are com-
plicated to align.
For a robust tracking, head pose and facial ac-
tions should be taken into account. The early proposal
(DeCarlo and Metaxas, 2000) to do so involves opti-
cal flow and and updates continuously during track-
ing to be adaptable to environmental changes. Opti-
cal flow can be very accurate but is not robust to fast
movements. Moreover, this approach accumulates er-
rors and drift away which is not easy to recover in
long video sequences. With the help of local features
which provides descriptors invariant to non-rigid mo-
tions, Chen and Davoine (Chen and Davoine, 2006)
took advantages of local features constrained by a 3d-
face paramerized model, called Candide-3, to capture
both rigid and non-rigid head motions. This method
does not need a huge-size pool of training data ei-
328
Tran N., Feldmar J., Charbit M., Petrovska-Delacrétaz D. and Chollet G..
3D Face Pose Tracking from Monocular Camera via Sparse Representation of Synthesized Faces.
DOI: 10.5220/0004345003280333
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 328-333
ISBN: 978-989-8565-48-8
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

ther: it generates learning data from synthesized faces
which is rendered from the first video frame. How-
ever, this approach suffers the following problem: the
learning model assumes Gaussian distributions of lo-
cal appearance and the candidate is chosen depends
on the minimum distance to mean vector; hence, it is
not realistic and possible to render more training faces
to be robust to profile-view. Ybanez et al (Yb
´
a
˜
nez-
Zepeda et al., 2007) and Lefevre et al (Lefevre and
Odobez, 2009) have adopted the same approach using
synthesized faces as training data. (Yb
´
a
˜
nez-Zepeda
et al., 2007) finds the linear correlation between 3d
model parameters and global appearance of stabilized
face images. This method is robust for face and land-
mark tracking but limited to frontal and near-frontal
faces. (Lefevre and Odobez, 2009) extended Candide
by collecting more appearance information from head
profiles by randomly choosing more points to repre-
sent facial appearance. Their error function consists
of structure and appearance features combined with
dynamic modeling. The minimization problem of this
function is of large dimension and is likely to fall into
local minimum.
In this paper, we adopt the sparse presentation
which is well-known in many applications (Wright
et al., 2009; Elad and Aharon, 2006; Mei and Ling,
2011), to build the tracking framework. We also
take advantage of a synthesized database (Chen and
Davoine, 2006; Yb
´
a
˜
nez-Zepeda et al., 2007; Lefevre
and Odobez, 2009) to circumvent the huge-size data
problem and adopt local features to be robust to rigid
and non-rigid changes. Why is sparse representation
useful in our context? (1) the database of synthesized
faces is not huge which is suitable to build dictionar-
ies or codebooks. (2) The codebooks are able to be
built by collecting not only positive samples but also
negative samples. (3) The method could search and
choose only the nearest neighbors from training data
to represent the observation by solving `
1
-norm prob-
lem (4) and the most important is that this method
can reconstruct the observation using training samples
that is likely a way to realize whether the observation
is good or not; moreover, the noise is probably re-
moved during reconstruction.
The remaining sections of this paper are organized
as follow: Section 2 gives some background on the
3d face model and the sparse representation. Section
3 shows the proposed framework for tracking using
sparse representation. Experimental results and anal-
ysis are presented in Section 4. Finally, we draw con-
clusions in Section 5.
Figure 1: Candide-3 model and 26 selected points for track-
ing in our framework and some examples of rendered im-
ages from frontal face using Candide-3.
2 RELATED WORKS
In this work, Candide model (Ahlberg, 2001) is used
to represent the 3d face model and create synthe-
sized images as learning data and sparse representa-
tion (Wright et al., 2009) which models a new face as
a sparse linear combination of learning faces.
2.1 3d Geometric Model
Candide-3 (Ahlberg, 2001) is a very commonly used
face shape model. It consists of 113 vertices and 168
surfaces. See Fig. 1 represents the frontal view of the
model. It is controlled both in translation, rotation,
shape and animation:
g(σ,α) = Rs (g + Sσ+ Aα) + t (1)
where g is 3N-dimensional mean shape (N = 113 is
the number of vertices) containing the 3d coordinates
of the vertices. The matrices S and A control respec-
tively shape and animation through σ and α param-
eters. And R is a rotation matrix, s is the scale, and
t is the translation vector. The model makes a weak
perspective assumption to project 3d face onto 2d im-
age. Like in (Chen and Davoine, 2006; Lefevre and
Odobez, 2009; Yb
´
a
˜
nez-Zepeda et al., 2007), only 6
dimensions r
a
of the animation parameter are used
to track eyebrows, eyes and lips. Therefore,the full
model parameter is in our framework has 12 dimen-
sions, consists of 3 dimensions of rotation (r
x
,r
y
,r
z
),
3 dimensions of translation (t
x
,t
y
,t
z
) and 6 dimen-
sions of animation r
a
:
b = [r
x
,r
y
,r
z
,t
x
,t
y
,t
z
,r
a
] (2)
Texture Model: In Candide model, appearance or
texture parameters are not available. Usually, we
warp and map the image texture onto the triangles of
the 3d mesh by the image projection.
2.2 Sparse Representation
In many applications based on a linear model, we
have to deal with a set of coefficients which almost
3DFacePoseTrackingfromMonocularCameraviaSparseRepresentationofSynthesizedFaces
329

all of them are equal to zero. This is particularly evi-
dent when the problem is highly under-determined. In
such cases we speak of sparsity representation. Spar-
sity representation has received a very large attention
during the last two decades in many data process-
ing applications (Tibshirani, 1996). Nowadays it is
well-known that introducing a `
1
-norm constraint on
the optimization problem, based for example on the
quadratic minimization, is able to force the sparsity
of the solution.
More recently for classification problem in image
processing, sparsity has been considered by (Wright
et al., 2009). Given a set A (training database) of K
different dictionaries, associated respectively to K ob-
ject classes, and let y a vector under testing, we may
expect that, if y belongs to the class i, it could be ex-
plained by only the dictionary A
i
. More specifically,
if we write that y ≈ Aα that α must be sparse:
ˆ
α
1
= argmin
k
α
k
1
sub ject to
k
Aα −y
k
2
2
< ε (3)
3 PROPOSED METHOD
Our framework consists of two steps: training and
tracking. The proposed framework is basically sim-
ilar to (Chen and Davoine, 2006) to create a database
of synthesized faces but we propose a new way of
tracking face poses. In this section, we describe our
method in detail.
3.1 Training
The campaign of acquisition of ground-truth is very
costly and the databases need often manual annota-
tion which is also time consuming. To circumvent
this drawback, many people used synthetic databases
(Chen and Davoine, 2006; Yb
´
a
˜
nez-Zepeda et al.,
2007; Lefevre and Odobez, 2009) generated with
Candide model. To collect training data, they do the
three following steps to obtain images using Candide
and building codebooks for the next tracking step:
3.1.1 3d Model Initialization
In the work of (Chen and Davoine, 2006), the authors
align manually the Candide model on the first video
frame Y
0
and warp and map the texture from the im-
age to the model. In our work, we manually annotate
several landmarks on the first video frame, then using
the POSIT algorithm (Dementhon and Davis, 1995)
we estimate the pose based on these landmarks and
the corresponding Candide model landmarks to get
the initial model parameters b
0
.
3.1.2 Data Generation
After initialization, the texture is warped and mapped
from the first video frame to the Candide model. We
obtain our training database by rendering model dif-
ferent shapes and views around this frontal image. Let
us remark that the full dimension of the parameters to
track is 12. Therefore, we cannot explore this space
finely. However,we can realize that the translation pa-
rameters t
x
and t
y
will not affect the face appearances
and although the different expressions (corresponding
to changes of animation parameters) can account non-
rigid motions which generate different face appear-
ance, it will not significantly influence local features.
Therefore, only the rotation are gridded for building
the training database. Specifically, 7 values of Pan
and Tilt and Roll from -30 to +30 by step 10 are taken
to create 7
3
= 343 pose views as Fig. 1.
3.1.3 Codebook Building
In our framework, we take advantage of sparse repre-
sentation like in (Wright et al., 2009) and it requires
to build linear codebooks as discussed at Eq. 6 of
Section 2.2. The framework adopts 26 local descrip-
tors as 9 × 9 squared blocks that form 81-dim vectors
around 26 landmarks as Fig. 1. Each codebook A
i
plays a role as learning data for landmark ith, it is a
matrix 81 × m where m is the number of training sam-
ples. It consists of 343 positive training samples of
ith landmarks extracted from the synthesized data and
m − 343 negative training samples chosen randomly
on first frame. The negative samples are very impor-
tant to reduce noise during reconstruction. it means
a tracked ith landmark, if it is good should approxi-
mately lie in the linear span of the training samples
and, ideally, very few coefficients associated to posi-
tive landmarks should have non-zero values.
3.2 Tracking
Our tracking method refers to the Likelihood ap-
proach which searches the efficient distribution
of p(Y
t
|b
t
) where Y
t
is the observation of land-
marks at time t and b
t
is the hidden state, b
t
=
(r
x
,r
y
,r
z
,t
x
,t
y
,t
z
,r
a
) is the 12-dimensional vector in
our context.
The tracking system starts from the frontal face
that Candide is fitted on, and then it finds the can-
didate of face in the next frame t from state vector
at time t − 1, with t = 0 at the first frame. In order
to obtain the hidden state b
t
at time t, we initialize
thirteen hidden states at time t from previous state:
b
t
= b
t−1
+ δ
b
to form a simplex, where δ
b
is cho-
sen randomly around previous state. The optimum
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
330

solution that can then be found, based on the sim-
plex using a derivative-free optimizer such as down-
hill simplex (Nelder and Mead, 1965). For each pa-
rameter b
t
, the 3d Candide is projected onto the next
2D frame at t to localize 2D landmark positions, and
the appearance texture Y
t
is concatenation of local tex-
tures y
i
(b
t
),i = {1,..., n} which are extracted around
the landmarks as the observed appearance. These ob-
servations can then be used to establish the observa-
tion model for tracking and the most important thing
is how to find the efficient observation model.
In (Chen and Davoine, 2006; Lefevre and Odobez,
2009), the authors assumed that the local appearances
around landmarks are independent and obey multi-
variate Gaussian distributions. So, the observation
model is defined as a joint probability of Gaussian
distributions and the tracking problem can be solved
as maximum likelihood problem of a non-linear func-
tion.
p(Y
t
|b
t
) =
n
∏
i=1
ϕ(y
i
(b
t
)|µ
i
,Σ
i
) (4)
where Y
t
= [y
1
(b
t
),y
2
(b
t
),..., y
n
(b
t
)], n is the num-
ber of landmarks, ϕ(y
i
(b
t
)|µ
i
,Σ
i
) denotes multivariate
Gaussian distribution of function value at observation
around the ith landmark y
i
(b
t
) with µ
i
and Σ
i
pre-
learned from rendered images during training. Tak-
ing the logarithm of likelihood, they finally attempt to
minimize the sum of Mahalanobis distance:
ˆ
b
t
= argmin
b
t
n
∑
i=1
k
y
i
(b
t
) −µ
i
k
2
Σ
−1
i
(5)
The key of their proposition is that all points are
assumed to be in an ellipsoid represented by a fixed
mean and covariance and the best observation is the
candidate which has the minimum distance to the
mean. It is not really realistic.
In our work, we tackle the problem from another
perspective with a similarity distance between the ob-
servation and its reconstruction from training samples
defined as follows:
ˆ
b
t
= argmin
b
t
n
∑
i=1
k
y
i
(b
t
) − ˆy
i
−
ˆ
ε
i
k
2
2
(6)
where ˆy
i
denotes the reconstruction of the observation
y
i
(b
t
) of ith landmark at time t from training data and
and
ˆ
ε
i
is the noise should be removed from the ob-
servation. In order to obtain the reconstruction and
noise, we attempt to minimize the problem:
{
ˆ
α
i
,
ˆ
ε
i
} = argmin
α
i
,ε
i
k
α
i
k
1
+
k
ε
i
k
1
st. A
i
α
i
+ ε
i
= y
i
(7)
where A
i
is the codebook of ith landmark. The re-
construction can be computed using ˆy
i
= A
i
ρ(
ˆ
α
i
) and
the function ρ(.) keeps only coefficients associates to
the positive ith landmarks in its codebook and others
are set zeros, see (Wright et al., 2009). The equation
(7) could be converted to a basic `
1
-norm problem of
coefficient vector [
ˆ
α
i
ˆ
ε
i
] and the codebook [A
i
I]:
{[
ˆ
α
i
ˆ
ε
i
]
T
} = argmin
α
i
,ε
i
[α
i
ε
i
]
T
1
st. [A
i
I]
α
i
ε
i
]
T
= y
i
(8)
where I is identity matrix and (8) can be solved using
(3). Equation (7) means that a new ith observed patch
y
i
on the frame should lie on span of linear combi-
nation of atoms of A
i
codebook with some noise. If
y
i
is a well-localized ith patch, the vector α
i
should
be sparse and very few coefficients associated to pos-
itive atoms of A
i
should be non-zero and the oppo-
site for negative atoms. This sparse vector brings
ρ(
ˆ
α
i
) ≈
ˆ
α
i
and the error reconstruction will be small.
To sum up, the better well-localized the landmark is,
the smaller the objective function gets. From another
point of view, for example in (Chen and Davoine,
2006; Lefevre and Odobez, 2009), the contribution of
all training samples is the same to find the best can-
didate, but there are many landmarks not actually re-
lated to current observation that can cause noise. It
is better to choose only the nearest neighbors around
the observation to contribute to the objective function
and our proposed function somehow is a quite rea-
sonable selection. It is illustrated in Fig. 2: the large
coefficients are associated to positive landmarks (red)
and the noise is reduced in reconstruction, whereas
the values of coefficients are distributed on both the
positive and negative sides in the case of negative ones
(yellow). Finally, this method makes no assumption
of Gaussian distribution of landmarks appearance as
in (Chen and Davoine, 2006; Lefevre and Odobez,
2009). In optimization context, the error function in
(6) with constraints (7) is a multi-dimensional func-
tion of model parameter b
t
which can be solved using
derivative-free optimizer as discussed above.
4 EXPERIMENTAL RESULTS
In order to evaluate the performance of our approach,
we used the Boston University Face Tracking (BUFT)
database(Cascia et al., 2000). This dataset con-
tains two subsets, uniform-light and varying-light,
where the ground-truth is captured by magnetic sen-
sors “Flock and Birds” with an accuracy of less than
1
o
. The uniform-light set has a total of 45 video se-
quences (320×240 resolution) for 5 subjects (9 videos
3DFacePoseTrackingfromMonocularCameraviaSparseRepresentationofSynthesizedFaces
331
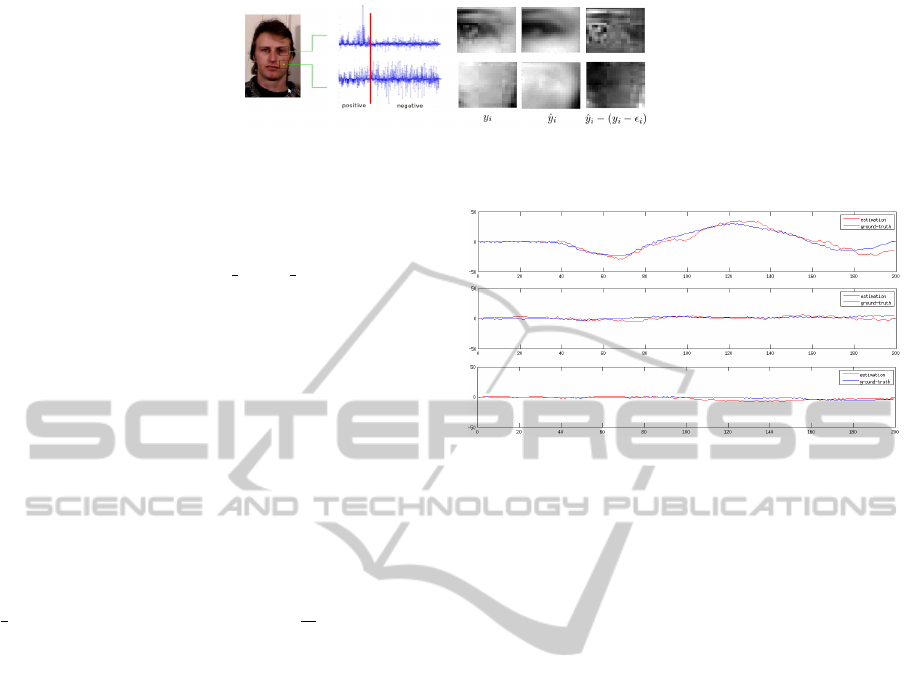
Figure 2: A visualization of observation, reconstruction and the error reconstruction of positive and negative landmarks. Large
coefficients are associated to the positive side for positive landmarks, whereas this is the opposite for negative landmarks.
per subject) and the second set of video sequences
for each of three subjects, they both have available
ground-truth formatted as (X pos, Y pos, depth, roll,
yaw (or pan), pitch (or tilt)). In this paper, we use the
first set to evaluate our methods.
For each frame of a video sequence, we use the
estimation of the rotation error e
i
= [θ
i
−
ˆ
θ
i
]
T
[θ
i
−
ˆ
θ
i
] like in (Lefevre and Odobez, 2009) to evaluate
the accuracy and robustness, where θ
i
and
ˆ
θ
i
are
(pan,tilt,roll) of the ground-truth and estimated pose
at frame i respectively. The robustness is the number
N
s
of frames tracked successfully and P
s
is the per-
centage of frames tracked over all videos. A frame
is lost when e
i
exceeds the threshold. The precision
includes the pan, tilt, roll and average rotation er-
rors (MAE measure) as the measure of tracker accu-
racy over tracked frames: E
pan
,E
tilt
,E
roll
and E
m
=
1
3
(E
pan
+ E
tilt
+ E
roll
) where E
pan
=
1
N
s
∑
i∈S
s
(θ
i
pan
−
ˆ
θ
i
pan
) (similarly for the tilt and roll) and S
s
is set of
tracked frames.
In our framework, we used the synthesized
database as discussed above, with 26 landmarks cho-
sen around the eyes, nose and mouth to build code-
books. For ith landmark, the codebook A
i
∈ R
343×1200
where the number of columns is 1200 which includes
343 positive samples and the remaining negative sam-
ples are chosen randomly. In order to solve the `
1
-
norm problem, we used the fast and efficient algo-
rithm described in (Yang et al., 2010).
For evaluation, we evaluate our performance with
framework of Chen and Davoine (Chen and Davoine,
2006) with and without using PCA to reduce the di-
mension of features before computing Mahalanobis
distances and compare to state-of-the-art methods.
We also evaluate the state-of-the-art of landmark
tracking (Saragih et al., 2011) and compare to our
work. As can be seen in Table 1, the Chen and
Davoine’s framework (Chen and Davoine, 2006) is
slightly worse than the second model using PCA for
feature reduction. Our proposed approach is better
than the two others both in terms of precision and ro-
bustness because we took into account the error of ob-
servation and found contributions only from the near-
est atoms as discussed above. Comparing to state-of-
the-art methods, we outperform (Cascia et al., 2000)
Figure 3: One example result on (jim1.avi) between our es-
timation and ground-truth. From first to third rows: Pan
error: 3.99, Tilt error: 2.32 and Roll error: 2.02.
at both the accuracy and robustness, slightly worse
than (Saragih et al., 2011) at robustness and finally
lower than remaining methods at both the robustness
and accuracy. The result shows that our method is still
not robust and gets a high error of Pan rotation when
the failure of tracker is caused by large Pan angle. For
example, several landmarks around one eye disappear
when the Pan is more than 30
o
and this leads to uncer-
tainty of observations around landmarks and makes
the tracker failed, see Fig. 3. And this is also the rea-
son causes the failure of robustness during tracking
in our framework. However, this problem could be
solved by generating more training data, using differ-
ent weights of landmarks or by making the observa-
tion model adaptive to changes of the environment.
5 CONCLUSIONS
In this paper, we propose a new way to deal with the
problem of face tracking using sparse representation.
In our method, we synthesize a database and local fea-
tures are extracted around landmarks to build code-
books. For tracking, an energy function which is the
sum of similarity distances between the observations
and their reconstructions using a sparse representa-
tion, is minimized. The result shows that the use of
a sparse representation is better than the use of mean
and covariance matrices to describe the observation
model. It suggests that mean and covariance matrices
in the same framework are inadequate to model the
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
332

Table 1: The comparison of robustness P
s
and accuracy (E
pan
, E
tilt
, E
roll
, E
avg
) between our method and state-of-the-art on
uniform-light set of BUFT dataset.
Approach P
s
E
pan
E
tilt
E
roll
E
avg
(Cascia et al., 2000) 75% 5.3 5.6 3.8 3.9
(Xiao et al., 2003) 100% 3.8 3.2 1.4 2.8
(Lefevre and Odobez, 2009) 100% 4.4 3.3 2.0 3.2
(Morency et al., 2008) 100% 5.0 3.7 2.9 3.9
(Saragih et al., 2011) 92% 3.9 3.9 2.3 3.4
Mahalanobis Distance (Chen and Davoine, 2006) 85% 5.1 3.8 2.0 3.6
PCA + Mahalanobis Distance 87% 5.2 3.5 2.0 3.6
Our model 89% 4.7 3.5 2.1 3.4
variations of appearance around landmarks. Although
performance is improved by our method, it remains
quite far from state-of-the-art methods. However, it
could be more efficient if the dynamical model or
state evolution was taken into account. Or the weights
of contribution to energy function were dependent on
the confidence of landmark observations at each time.
Finally the observation model could also be adapted
to changes through frames and be made more robust
for face tracking and pose estimation.
ACKNOWLEDGEMENTS
This work was financially supported by the ANR-
CONTINT-ORIGAMI2 project (ANR-10-CORD-
0016) and the LTCI of the Telecom-ParisTech
Institute, France.
REFERENCES
Ahlberg, J. (2001). Candide-3 - an updated parameterised
face. Technical report, Dept. of Electrical Engineer-
ing, Linkping University, Sweden.
Cascia, M. L., Sclaroff, S., and Athitsos, V. (2000). Fast,
reliable head tracking under varying illumination: An
approach based on registration of texture-mapped 3d
models. IEEE Trans. PAMI, 22(4):322–336.
Chen, Y. and Davoine, F. (2006). Simultaneous tracking of
rigid head motion and non-rigid facial animation by
analyzing local features statistically. In BMVC.
Cootes, T. F., Edwards, G. J., and Taylor, C. J. (1998). Ac-
tive appearance models. TPAMI, pages 484–498.
Cootes, T. F. and Taylor, C. J. (1992). Cj.taylor, ”active
shape models - ”smart snakes. In BMVC.
DeCarlo, D. and Metaxas, D. N. (2000). Optical flow con-
straints on deformable models with applications to
face tracking. IJCV, 38(2):99–127.
Dementhon, D. F. and Davis, L. S. (1995). Model-based
object pose in 25 lines of code. IJCV, 15:123–141.
Elad, M. and Aharon, M. (2006). Image denoising via
sparse and redundant representations over learned dic-
tionaries. IEEE Transactions on Image Processing,
15(12):3736–3745.
Gross, R., Matthews, I., and Baker, S. (2006). Active ap-
pearance models with occlusion. IVC, 24(6):593–604.
Lefevre, S. and Odobez, J.-M. (2009). Structure and ap-
pearance features for robust 3d facial actions tracking.
In ICME.
Mei, X. and Ling, H. (2011). Robust visual tracking and
vehicle classification via sparse representation. IEEE
Trans. PAMI, 33(11):2259–2272.
Morency, L.-P., Whitehill, J., and Movellan, J. R. (2008).
Generalized adaptive view-based appearance model:
Integrated framework for monocular head pose esti-
mation. In FG.
Nelder, J. A. and Mead, R. (1965). A simplex algorithm
for function minimization. Computer Journal, pages
308–313.
Saragih, J. M., Lucey, S., and Cohn, J. F. (2011). De-
formable model fitting by regularized landmark mean-
shift. IJCV, 91:200–215.
Tibshirani, R. (1996). Regression shrinkage and selection
via the lasso. Journal of the Royal Statistical Society
(Series B), 58:267–288.
Vacchetti, L., Lepetit, V., and Fua, P. (2004). Stable real-
time 3d tracking using online and offline information.
IEEE Trans. PAMI, 26(10):1385–1391.
Wright, J., Yang, A., Ganesh, A., Sastry, S., and Ma, Y.
(2009). Robust face recognition via sparse represen-
tation. TPAMI, 31(2):210 –227.
Xiao, J., Baker, S., Matthews, I., and Kanade, T. (2004).
Real-time combined 2d+3d active appearance models.
In CVPR.
Xiao, J., Moriyama, T., Kanade, T., and Cohn, J. (2003).
Robust full-motion recovery of head by dynamic tem-
plates and re-registration techniques. International
Journal of Imaging Systems and Technology, 13:85 –
94.
Yang, A. Y., Ganesh, A., Zhou, Z., Sastry, S., and Ma, Y.
(2010). A review of fast l1-minimization algorithms
for robust face recognition. CoRR, abs/1007.3753.
Yb
´
a
˜
nez-Zepeda, J. A., Davoine, F., and Charbit, M. (2007).
Local or global 3d face and facial feature tracker. In
ICIP, volume 1, pages 505–508.
3DFacePoseTrackingfromMonocularCameraviaSparseRepresentationofSynthesizedFaces
333
