3D Gesture Recognition by Superquadrics
Ilya Afanasyev and Mariolino De Cecco
Mechatronics Lab., University of Trento, via Mesiano, 77, Trento, Italy
Keywords: Superquadrics, Gesture Recognition, Microsoft Kinect, RANSAC Fitting, 3D Object Localization.
Abstract: This paper presents 3D gesture recognition and localization method based on processing 3D data of hands in
color gloves acquired by 3D depth sensor, like Microsoft Kinect. RGB information of every 3D datapoints
is used to segment 3D point cloud into 12 parts (a forearm, a palm and 10 for fingers). The object (a hand
with fingers) should be a-priori known and anthropometrically modeled by SuperQuadrics (SQ) with certain
scaling and shape parameters. The gesture (pose) is estimated hierarchically by RANSAC-object search
with a least square fitting the segments of 3D point cloud to corresponding SQ-models: at first – a pose of
the hand (forearm & palm), and then positions of fingers. The solution is verified by evaluating the
matching score, i.e. the number of inliers corresponding to the appropriate distances from SQ surfaces and
3D datapoints, which are satisfied to an assigned distance threshold.
1 INTRODUCTION
Gesture recognition, having the goal of interpreting
human gestures via mathematical algorithms, is the
important topic in computer vision with many
potential applications such as human-computer
interaction, sign language recognition, games, sport,
medicine, video surveillance, etc. The model-based
methods of hand gesture tracking have been studied
by a high number of researchers (Rehg and Kanade,
1995); (Starner and Pentland, 1995); (Heap and
Hogg, 1996); (Zhou and Huang, 2003); (La Gorce,
et al., 2008). Some publications used hand tracking
by color gloves with data acquired by fixed-position
webcams (Geebelen et al., 2010) or a single camera
(Wang and Popović, 2009). The hand tracking with
quadrics was used by the authors (Stenger et al.,
2001), but they had a model consisted of 39
quadrics, representing only palm and fingers.
The proposed method of 3D gesture recognition
by SQ is close to the corresponding hierarchical
method (Afanasyev et al., 2012) for 3D Human
Body pose estimation by SQ applied for processing
3D data captured by a multi-camera system and
segmented by a special preprocessing clothing
algorithm. In this paper, the object of recognition is
hand gesture; the sensor is MS Kinect; 3D point
cloud segmentation is provided by analyzing Kinect
RGB-depth data of color gloves. As far as a hand
and fingers can be a priori modeled with
anthropometric parameters in a metric coordinate
system, we propose using the hierarchical
RANSAC-based model-fitting technique with the
composite SQ-models. As known SQs can be used
for description of complex-geometry objects with
few parameters and generation of a simple
minimization function of an object pose (Jaklic et
al., 2000) and (Leonardis et al., 1997). The logic of
3D Gesture Recognition algorithm is clarified by the
block diagram (Fig. 1).
The gesture recognition starts with pre-
processing 3D datapoints (captured by MS Kinect),
segmenting them into 12 parts (forearm, palm and
10 for fingers) according to colors of gloves. Then
the algorithm recovers 3D pose of the hand as the
largest object (“Hand Pose Search”) and after that
restores fingers pose (“Fingers Pose Search”). To
cope with measurement noise and outliers, the Pose
Search is estimated by RANSAC-SQ-fitting
technique. The fitting quality is controlled by inlier
thresholds (for hand & fingers), which are a ratio of
the optimal amount of inliers to whole data points.
The tests showed that Hand Pose Search can give a
wrong palm position satisfying a palm threshold, but
troubling Fingers Pose Search. For this reason, when
a finger inliers solution less than a finger threshold,
the algorithm restarts the Hand Pose Search again
until finding suitable results for every fingers.
429
Afanasyev I. and De Cecco M..
3D Gesture Recognition by Superquadrics.
DOI: 10.5220/0004348404290433
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 429-433
ISBN: 978-989-8565-48-8
Copyright
c
 2013 SCITEPRESS (Science and Technology Publications, Lda.)

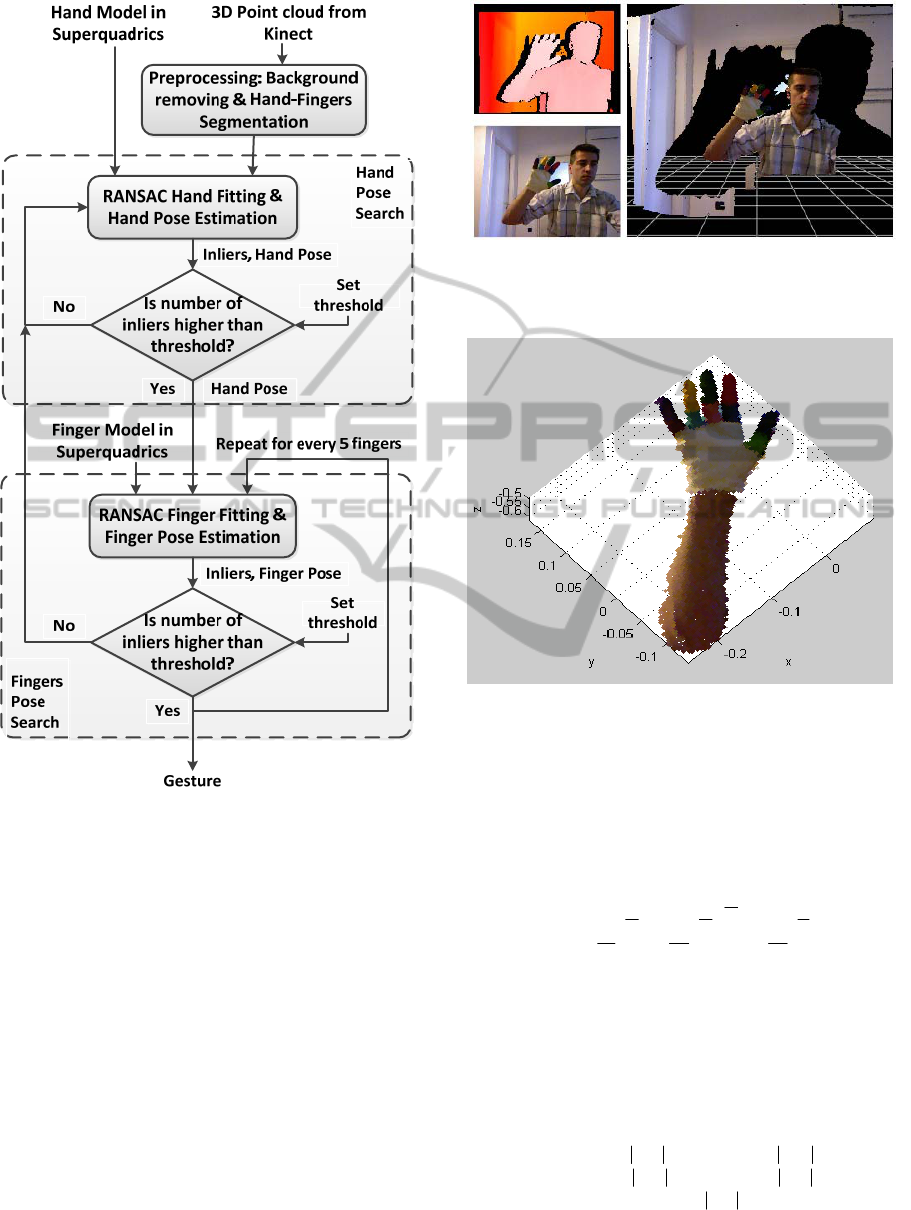
Figure 1: The block diagram of 3D Gesture Recognition
algorithm.
2 3D GESTURE RECOGNITION
ALGORITHM
2.1 About 3D Sensor and Data
The proposed method of 3D gesture recognition
works with 3D sensors captured 3D coordinate and
color information, like RGB-D (Red Green Blue -
Depth) cameras, multicamera systems, etc. We used
MS Kinect with 3D scanning software “Skanect”
developed by Nicolas Burrus (Burrus, 2011). The
software corrects the image distortions and captures
3D object rawdata in a metrical coordinate system
with the origin at Kinect 3D depth sensor (Fig. 2, 3).
Figure 2: Images acquired by Kinect RGB camera (left,
bottom) and Kinect 3D depth sensor (left, top); combined
image from Skanect software (right).
Figure 3: 3D cloud point of a hand with a color glove
captured by Kinect with color segmentation.
2.2 Superquadric Parameters
The implicit SQ equation is well suited to
mathematical modeling for fitting 3D data (Jaklic et
al., 2000) and (Leonardis et al., 1997):
()
1
1
2
22
2
3
2
2
2
1
,,
ε
ε
ε
εε
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
a
z
a
y
a
x
zyxF

(1)
where x, y, z – superquadric coordinate system;
a
1
, a
2
, a
3
– scale parameters of the object;
ε
1
, ε
2
– object shape parameters.
The explicit SQ equation is used for SQ
visualization (where η, ω – spherical coordinates):
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⋅⋅
⋅⋅⋅⋅
⋅⋅⋅⋅
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
1
21
21
sin)(sin
sin)(sincos)(cos
cos)(coscos)(cos
3
2
1
ε
εε
εε
ηη
ωωηη
ωωηη
signuma
signumsignuma
signumsignuma
z
y
x

(2)
Figure 3 illustrates 3D point cloud of hand & finger
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
430

modeled in 12 superquadrics – superellipsoids with
the shape parameters ε
1
= ε
2
= 0.6 and the following
scaling parameters for:
- Forearm: a
1
= a
3
= 0.025, a
2
= 0.115 (m).
- Palm: a
1
= a
3
= 0.04, a
2
= 0.018 (m).
- Phalange: a
1
= a
3
= 0.008, a
2
= 0.027 (m).
2.3 Hand & Fingers in Superquadrics
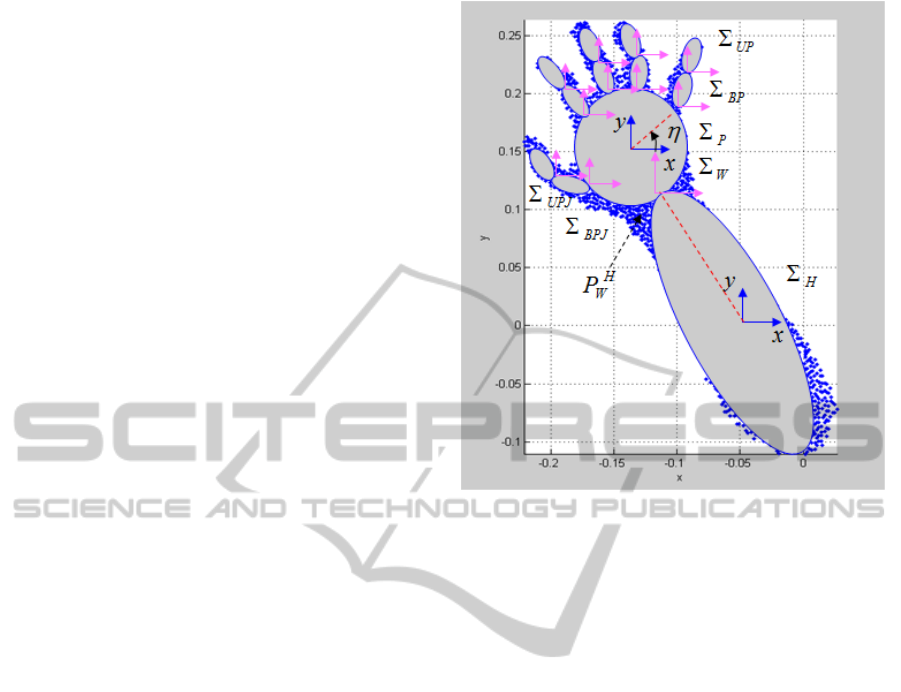
2.3.1 Transformation for a Hand
SQ position of a Hand is defined by rotations α, β, γ
among x, y, z (clockwise) correspondingly and the
translation of SQ center (x
c
, y
c
, z
c
) along x, y, z. The
transformation matrix T
H
for the HAND is:
where
z
y
x
RT
c
c
c
HH
,
1000
100
010
001
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⋅=
() ()
() ()
() ()
() ()
()
(
)
() ()
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
⋅
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
⋅
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
=
1000
0100
00cossin
00sincos
1000
0cos0sin
0010
0sin0cos
1000
0cossin0
0sincos0
0001
γγ
γγ
ββ
ββ
αα
αα
H
R
(3)
2.3.2 Transformations Hand – Wrist, and
Bottom – Upper Phalange Joint
The transformations Hand - Wrist (H-W) and
Bottom – Upper Phalange Joint (BP-UPJ) are the
similar and correspond to the matrix:
,
1000
100
010
001
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
==
L
L
H
W
BP
UPJ
H
W
P
TT
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
==
0
0
2
aPPwhere
BP
UPJ
H
W

(4)
2.3.3 Transformation Wrist - Palm
The transformation Wrist - Palm (W-P) is calculated
by rotations ξ, ρ, σ among x, z, y (clockwise)
correspondingly and the translation of SQ center on
distance a
2
along y.
()
,
1000
0100
010
0001
,,
2
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⋅==
a
RTT
W
P
W
P
W
P
σρξ

(5)
where R
P
W
is the rotation matrix of Palm:
() ()
() ()
()
(
)
() ()
() ()
() ()
.
1000
0cos0sin
0010
0sin0cos
1000
0100
00cossin
00sincos
1000
0cossin0
0sincos0
0001
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
⋅
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
⋅
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
=
σσ
σσ
ρρ
ρρ
ξξ
ξξ
W
P
R
(6)
Figure 4: Presentation of Hand in 12 parts: H – hand, P –
palm, W – wrist, BPJ/UPJ – Bottom/Upper Phalange
Joints, BP/UP – Bottom/Upper Phalanges, etc.
2.3.4 Transformation: Palm – Bottom
Phalange Joint
The transformation Palm – Bottom Phalange Joint
(P-BPJ) corresponds to the matrix:
,
1000
100
010
001
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
L
L
P
BPJ
P
BPJ
P
T
()
()
.
0
sin
cos
2
1
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
η
η
a
a
Pwhere
P
BPJ

(7)
2.3.5 Transformation: Bottom Phalange
Joint - Bottom Phalange
The transformation Bottom Phalange Joint – Bottom
Phalange (BPJ-BP) is created by rotations δ and ε
among x and z (clockwise) correspondingly and the
translation of SQ center on –a
2
along y.
() ()
() ()
(
)()
() ()
.
1000
0100
010
0001
1000
0100
00cossin
00sincos
1000
0cossin0
0sincos0
0001
2
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
⋅
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
=
a
T
BPJ
BP
εε
εε
δδ
δδ
(8)
2.3.6 Transformation: Upper Phalange Joint
- Upper Phalange
The transformation Upper Phalange Joint - Upper
Phalange (UPJ-UP) is created by the rotation θ
3DGestureRecognitionbySuperquadrics
431

among x (clockwise) and the translation of SQ
center on –a
2
along y.
()
() ()
() ()
1
2
1000
0cossin0
sincos0
0001
−
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
=
θθ
θθ
θ
a
T
UPJ
UP

(9)
2.3.7 Full Transformation: Hand – Upper
Phalange
Finally, taking into account equations (4)-(9), the
full transformation for every point of system “Hand
– Upper Phalange” (H-UP) is:
()
HUPJ
UP
BP
UPJ
BPJ
BP
P
BPJ
W
P
H
W
UP
PTTTTTTP ⋅⋅⋅⋅⋅⋅=
−1

(10)
where P
H
, P
UP
– coordinates of Hand and Upper
Phalange points correspondingly (Figure 3).
2.4 RANSAC-SQ-Fitting Algorithm
The Hand and Fingers Pose Searches are very
similar and have the common logic (Figure 1).
RANSAC Hand Fitting algorithm is used to find the
hand pose hypothesis, i.e. 6 variables: 3 rotation (α,
β, γ) and 3 translation coordinates (x
C
, y
C
, z
C
). These
variables are needed to calculate the transformation
matrix T
H
(3). The model described by the
superquadric implicit equation (1) is fitted to 3D
datapoints sorted by segmentation. Each RANSAC
sample calculation is started by picking a set of
random points (s = 6) in the world coordinate system
(x
Wi
, y
Wi
, z
Wi
). The following equation is used to
transform these points to the SQ centered coordinate
system (x
Si
, y
Si
, z
Si
):
,
1
),,(
1
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⋅=
−
i
i
i
iiii
w
w
w
HANDssss
z
y
x
TzyxF

(11)
where
1−
HAND
T
is the matrix of inverting homogeneous
transformation for the hand (3).
Then the inside-outside function is calculated
according to the superquadric implicit equation (1)
in world coordinate system:
.
)()()(
1
1
2
22
2
3
2
2
2
1
ε
ε
ε
εε
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
a
zF
a
yF
a
xF
F
iii
i
ssssss
w

(12)
The inside-outside function for superquadrics has 11
parameters (Jaklic et al., 2000) and (Solina and
Bajcsy, 1990):
),,,,,,,,,,,,,,(
21321 cccWWWw
zyxaaazyxFF
iiii
χ
β
α
ε
ε
=

(13)
where 5 parameters of the SQ size and shape are
known (a
1
, a
2
, a
3
, ε
1
, ε
2
) and other 6 parameters (α,
β, γ, x
C
, y
C
, z
C
) should be found by minimizing the
cost-function:
(
) ,1)(min
2
1
2
1
−=
∑
=
ε
i
W
w
s
i
ii
F
FxF

(14)
where additional exponent ε
1
ensures that the points
of the same distance from SQ surface have the same
values of F
W
(Solina and Bajcsy, 1990).
SQ fitting to the random dataset by minimizing
the inside-outside function of distance to SQ surface
is realized by nonlinear least-square minimization
method with “Trust-Region algorithm” (or
“Levenberg-Marquardt algorithm”). The amount of
inliers is estimated by comparing the distances
between every point of 3D point cloud and SQ
model with distance threshold t (t = 1 cm):
(
)
.1
2
321
1
−⋅⋅⋅=
ε
i
wi
Faaad

(15)
3 RESULTS
The Figure 5 shows the workability of the
RANSAC-based model-fitting the composite SQ-
model to 3D point cloud for Gesture Recognition.
The presented example concludes 4848 points of 3D
data, achieving about 65% of inliers for distant
threshold 1 cm. The algorithm has been developed in
MATLAB. The RGB-D information was obtained
with Microsoft Kinect and then processed offline
(taking about several minutes for a gesture). The
quality of gesture recognition depends on quality of
segmentation that requires good illumination
condition and using gloves with bright colors. For
some gestures (when fingers are hidden) the method
cannot correctly recognize the finger poses.
4 CONCLUSIONS
The paper describes a method of 3D Gesture
Recognition by SuperQuadrics (SQ) from 3D point
cloud data captured by Microsoft Kinect and
clustered according to the colors of the color gloves.
The hand was modeled by a composite SQ-model
consisted of forearm, palm and fingers with a-priori
known anthropometric dimensions. The proposed
method based on hierarchical RANSAC-pose search
with a robust least square fitting SQs to 3D data: at
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
432

first for the hand, then for the fingers. The solution
is verified by evaluating the matching score and
comparing this score with admissible inlier threshold
for the hand and fingers. The gesture estimation
technique described has been tested by processing
3D data offline, giving encouraging results.
ACKNOWLEDGEMENTS
The work of Ilya Afanasyev on creating the
algorithms of 3D Gesture recognition has been
supported by the grant of EU\FP7-Marie Curie-
COFUND-Trentino postdoc program, 2010-2013.
The authors are very grateful to colleagues from
Mechatronics Lab., UniTN, for help and support.
REFERENCES
Afanasyev I., Lunardelli M., De Cecco M., et al. 2012. 3D
Human Body Pose Estimation by Superquadrics. In
Conf. Proc. VISAPP’2012 (Rome, Italy), V.2, 294-302.
Burrus N. Kinect software “Skanect-0.1”. 2011.
http://manctl.com/products.html.
Heap A.J. and Hogg D.C., 1996. Towards 3-D hand
tracking using a deformable model. In Conf. Proc. on
Face and Gesture Recognition, P.140–145.
Geebelen G., Cuypers T., Maesen S., and Bekaert P.,
2010. Real-time hand tracking with a colored glove.
In Conf. Proc. 3D Stereo Media.
Jaklic A., Leonardis A., Solina F., 2000. Segmentation and
Recovery of Superquadrics. Computational imaging
and vision 20, Kluwer, Dordrecht.
La Gorce M., Paragios N., Fleet D., 2008. Model-Based
Hand Tracking with Texture, Shading and Self-
occlusions. In IEEE Conf. Proc. CVPR. P.1-8.
Leonardis A., Jaklic A., Solina F., 1997. Superquadrics for
Segmenting and Modeling Range Data. In IEEE Conf.
Proc. PAMI-19 (11). P. 1289-1295.
Rehg J.M. and Kanade T., 1995. Model-based tracking of
self-occluding articulated objects. In IEEE Conf. Proc.
on Computer Vision, P. 612–617.
Solina F. and Bajcsy R., 1990. Recovery of parametric
models from range images: The case for superquadrics
with global deformations. IEEE Transactions PAMI-
12(2):131-147.
Stenger B., Mendonca P.R.S., and Cipolla R., 2001.
Model-based 3D tracking of an articulated hand. In
IEEE Conf. Proc. CVPR 2001 (2): 310-315.
Starner T. and Pentland A., 1995. Real-time american sign
language recognition from video using hidden Markov
models. In IEEE Proc. Computer Vision, P. 265-270.
Wang R.Y. and Popović J., 2009. Real-time hand-tracking
with a color glove. ACM Transactions on Graphics
(TOG), 28 (3), 63.
Zhou H. and Huang T. S., 2003. Tracking articulated hand
motion with eigen dynamics analysis. In IEEE Conf.
Proc. on Computer Vision, V. 2, P. 1102–1109.
APPENDIX
Figure 5: 3D gesture recognition by Superquadrics.
3DGestureRecognitionbySuperquadrics
433