SoftGrid: A Green Field Approach of Future Smart Grid

Yayun Zhou

, Harald Held

, Wolfram Klein

, Kurt Majewski

, Rainer Speh

Philipp Emanuel Stelzig

and Christoph Wincheringer

Siemens AG, Corporate Technology, RTC AUC MST-DE, Otto-Hahn-Ring 6, Munich, Germany

Siemens AG, Corporate Technology, RTC BAM ORD-DE, Otto-Hahn-Ring 6, Munich, Germany

Siemens AG, Corporate Technology, RTC AUC MSP-DE, Otto-Hahn-Ring 6, Munich, Germany

Siemens AG, Infrastructure & Cities Sector Strategy, IC ST TI, Otto-Hahn-Ring 6, Munich, Germany

Keywords:

SoftGrid, Renewable Energy, Decentralized System, Optimization, Automation, Two-level Control.

Abstract:

In this paper, a novel power grid solution “SoftGrid” is proposed, which is a decentralized power system with

two-level control architecture. The basic unit of this grid solution is a so-called SoftGrid-Adapter (SGA),

which controls generators, consumers as well as energy storage devices under the guidance of an optimization

model. The energy transmission among SGAs is supervised by a SoftGrid-Dispatcher (SGD), which balances

energy among SGAs. Using the proposed SoftGrid two-level control architecture, one can build up a local

grid from scratch. It is especially well-suited to be applied in remote areas where no commercial power grid

exists. Hence it is also viewed as a green ﬁeld approach to a future smart grid. The concept of SoftGrid is

veriﬁed through system modeling and simulation under different scenarios. The simulation results show that

SoftGrid is a power grid solution with both ﬂexibility and reliability.

1 INTRODUCTION

Today’s alternating current (AC) power grid is based

on Nikola Tesla’s design published in 1888 (Tesla,

1888). At that time, the grid was conceived as a local

grid with a demand-driven control function. Those

electricity systems were usually operated locally by

cities or industries. As power grids grew over time,

some of them were interconnected for economic and

reliability reasons in the early 20th century. After sev-

eral decades’ development, the electric grids in de-

veloped countries have become very large and highly

interconnected. In such grid systems, the power is

generated in “central” generation power stations and

delivered to major load centers to provide power to

smaller industrial and domestic users over the entire

supply area. In such centralized power system, the

number of power stations had to increase in order to

satisfy the increasing user demand. When the increas-

ing number of power stations cannot keep up with the

increasing demand of users, it results in poor power

quality including blackouts and power cuts. Since the

user demand varies from time to time, the grid capac-

ity designed to meet the peak time demand usually

leads to idle resources in average time. It remains as

one of the limitations of the traditional electrical grid

until the improvements of electronic communication

technology ﬁnally provide a possibility to guide user

demand in early 21st century. At that time, the in-

tension to integrate highly variable renewable energy

such as wind power and solar power into the existing

grid leads to the need for more sophisticated control

systems. Herein, the concept “smart grid” (Siemens,

2012) becomes very popular for it allows for sys-

tematic communication between suppliers and con-

sumers and permits both the suppliers and the con-

sumers to be more ﬂexible and sophisticated in their

operational strategies. Fig. 1 shows the evolutionary

process of power grids. The move from a traditional

grid to a smart grid is a move from a centralized,

producer-controlled network to a less centralized and

more consumer-interactive network.

Researches and market reports have shown that

the upgrade from traditional grid to smart grid can

bring in substantial beneﬁts such as improvement of

reliability by reducing power quality disturbances;

improvement of efﬁciency by reducing the cost to

produce, deliver, and consume electricity; protection

of environment and reduction of emissions by inte-

grating renewable energy resources; improvement of

safety and security by reducing the probability and

consequences of man-made attacks and natural disas-

Zhou Y., Held H., Klein W., Majewski K., Speh R., Stelzig P. and Wincheringer C..

SoftGrid: A Green Field Approach of Future Smart Grid.

DOI: 10.5220/0004356500050011

In Proceedings of the 2nd International Conference on Smart Grids and Green IT Systems (SMARTGREENS-2013), pages 5-11

ISBN: 978-989-8565-55-6

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Evolutionary Process of Power Grids.

ters (Dodrill, 2010). Nevertheless, current smart grid

projects are mostly carried out in developed coun-

tries to modernize their grid systems. There is still

a market vacancy in remote areas and less developed

countries, where no commercial grids are available.

In those areas, the population density is often low

and residents usually live far from each other. Since

long distance transmission brings in energy losses, a

more reasonable solution is to employ power gener-

ation and energy storage at a local level. This dis-

tributed generation concept allows collection of en-

ergy from many sources, providing higher power re-

liability and security with fewer environmental con-

sequences compared with traditional power genera-

tors. However, application of individual distributed

generators can cause many problems. A better way to

realize the emerging potential of distributed genera-

tion is to take a system approach which views genera-

tion and associated loads as a subsystem or a “micro-

grid” (Lasseter and Mettam, 2004)(Mohamed, 2008).

Similar to “microgrid”, our power grid solution

aims to serve decentralized systems. It does not rely

on the existing commercial grids and is able to operate

in a stand-alone mode. The basic unit of SoftGrid is a

SoftGrid-Adapter (SGA), which controls generators,

consumers and energy storage devices of typically a

household or a small business under the guidance of

an optimization model. It balances the power supply

capacity and user demands by scheduling generation

and consumption at a local level. Those basic units

can connect with each other, building up a grid from

bottom to up. Therefore, SoftGrid is especially ap-

plicable in remote areas with no existing energy grid.

Moreover, it provides the option for stepwise invest-

ments and installations, starting with a single SGA,

adding others and interconnecting them to a local ex-

ecutable grid. The energy transmission among SGAs

is supervised by a SoftGrid-Dispatcher (SGD), which

balances both the energy supplies and demands in this

local network. Furthermore, the SGD regulates the

power ﬂow and enables the local grid to be integrated

to an available external power grid. Fig. 2 shows the

two-level control architecture of SoftGrid. With this

Figure 2: Two-level Control Architecture of SoftGrid.

two-level control architecture, SoftGrid combines the

advantages of smart grid and microgrid, providing a

reliable and ﬂexible local grid which optimizes the

power ﬂow through sophisticated optimization mod-

els.

In this paper, the concept of SoftGrid is proposed

and veriﬁed through components modeling and user

demand simulation under different scenarios. The

rest of the paper is organized as followings: Firstly,

the system model of SoftGrid is introduced in Sec-

tion 2. The component models in a SoftGrid system

are implemented and stored in a library in the CoS-

MOS (Complex Systems Modeling, Optimization and

Simulation), which is a simulation and optimization

software developed by our group

. Then the software

structure of SoftGrid is brieﬂy introduced in Sec-

tion 3. It is developed based on the server-client ar-

chitecture. Afterwards, the principles of the optimiza-

tion model construction in the SGA and the SGD are

revealed in Section 4. The optimization problems are

solved by the CoinOR Solvers Ipopt and CBC (COIN-

OR, 2012). To verify the concept under different op-

eration environments, different examples are tested.

Some simulation results are shown in Section 5. Fi-

nally, a conclusion is drawn in Section 6.

2 SYSTEM MODEL

A SoftGrid system comprises ﬁve categories of com-

ponents: generator, consumer, storage device, con-

trol device and assistant component. The genera-

tor category not only includes renewable energy de-

vices, such as photovoltaic panels, biomass genera-

Siemens AG, Corporate Technology, Research & Tech-

nology Center, Research Field Automation & Control, Re-

search Group Simulation Germany

SMARTGREENS2013-2ndInternationalConferenceonSmartGridsandGreenITSystems

tors and wind turbines, but also allows the possible

use of traditional energy resources, such as diesel gen-

erators. The generator models refer to (Mohamed,

2008)(Gonzalez-Longatt, 2006)(Jurado et al., 2003).

The various electric consumption devices in a house-

hold are further categorized into three types: ﬁxed-

proﬁle consumer, deferrable consumer, and energy-

control consumer. The ﬁxed-proﬁle consumer oper-

ates according to a load proﬁle that models the user

demand with respect to time. Most household ap-

pliances can be modeled as ﬁxed-proﬁle consumers,

such as light, refrigerator, television and fan. The de-

ferrable consumer has a user-deﬁned operation pat-

tern and the operation time can be shifted within a cer-

tain time period. Typical example of a deferrable con-

sumer are washing machine and dishwasher, whose

operation pattern is pre-programmed (typically ﬁll,

wash, spin or ﬁll, wash, heat) and the start of oper-

ation time can be optimized to minimize the cost or

maximize the energy usage. The energy-control con-

sumer is a device which transforms the electric energy

into another form in order to store the energy or use it

for certain purpose. A typical example of an energy-

control consumer is water pump that pumps water to

a tank or an irrigation device.

indent The usual storage device in the SoftGrid sys-

tem is a battery. It is critical to balance the electric-

ity demand and electricity supply to prevent deep dis-

charge of the battery and idle resources caused by a

full battery. Hence, a circuit based battery model is

adopted and simpliﬁed according to the simulation

need (Salameh et al., 1992)(Appelbaum and Weiss,

1982). A SoftGrid system has two types of control

devices: SGA and SGD. SGA is the ﬁrst level con-

trol device, which controls the operation of genera-

tor, and consumers with while monitoring the battery

state of charge (SOC). It optimizes the energy allo-

cation based on demand prognosis and power genera-

tion capacity prediction. SGD is the second level con-

trol device, which monitors the energy generation and

consumption status in the local SGAs. Once energy

shortage is foreseen in one of the interconnected local

SGAs, the SGD will command other SGAs with en-

ergy residual to support the SGAs with energy short-

age in order to keep the user demands satisﬁed in the

whole system. The objective function of SGD fulﬁlls

the function to satisfy user-demands, charge storage

devices, as well as minimize the transmission loss.

The assistance components are the components that

complete the system conﬁguration, such as electric

transmission line, resister and DCDC-Converter. All

the component models are implemented and stored in

a library.

Fig. 3 shows some components implemented in

Figure 3: Some Simulation Component Models imple-

mented in the SoftGrid System.

the SoftGrid library. In this library, each system com-

ponent corresponds to a unique graphic symbol. The

component model is implemented independently and

connected later to constitute a complex system. New

components can be added to the SoftGrid library in

case of system extension. Each component provides a

user interface that enables the user to set and change

parameters. Fig. 4 shows an example of parameter

setting menu of a component. Those components are

the basic elements. Different test scenarios are con-

structed by changing grid topology and component

parameters.

Figure 4: User Interface of Consumer.

3 SIMULATION SYSTEM

The SoftGrid system is implemented under the frame-

work of CoSMOS (Complex Systems Modeling, Op-

timization and Simulation). It is a simulation tool de-

veloped by our group to simulate and optimize com-

plex systems in different application areas. CoS-

MOS is a model based simulation tool with a client-

server architecture. The components in a complex

system are associated with mathematical models (typ-

SoftGrid:AGreenFieldApproachofFutureSmartGrid

ically partial differential equations (PDEs) and alge-

braic equations). Each component contains four parts:

terminals, equations, parameters and extern-system-

variables. Terminals are used to connect other compo-

nents, for example in an electrical or control manner,

in order to generate a system. From a mathematical

point of view, when two components are connected,

certain equations are formed. Those equations stand

for the component model. Each component is char-

acterized by different parameters and extern-system-

variables are used to exchange data between different

clients through the server.

Fig. 5 shows the software structure of the Soft-

Grid simulation system. The SoftGrid component li-

brary stores all components which are implemented

according to system models introduced in the previ-

ous section. The chosen components are connected

to set up a local grid network. In a SoftGrid test,

three main processes are evolved: simulation, opti-

mization, and automation. The simulation solves the

electric network system and simulates the power ﬂow

inside the local network. The optimization serves as

a headquarter deciding the power allocation for each

component. The automation keeps the system robust

against unexpected situations, such as sudden weather

change and device failure. The PowerBridge is a de-

centralized communications unit, which enables op-

erators of solar or wind power facilities to logon to

a virtual power plant through the Internet with just a

few mouse clicks.

Figure 5: Software Architecture of SoftGrid System.

In the simulation process, the electricity demands

are modeled as stochastic time series, which mimic

the random behavior of users. The environmental im-

pact is also considered as a stochastic process. The

expectation value of the time series are used in the

optimization process as predictions of electricity de-

mands and electricity supplies. An automation pro-

cess checks the status of energy storage devices in or-

der to keep the system stable. The communication

between these three processes is carried out by the

corresponding clients. Fig. 6 shows the synchroniza-

tion of these three processes.

Figure 6: Synchronization of Simulation, Optimization and

Automation.

4 OPTIMIZATION MODEL

There are two types of optimization problems in the

SoftGrid system. In the basic control unit SGA, the

key purpose is to keep a performance balance be-

tween the different consumers and generators con-

nected to the local SGA and exploit all available en-

ergy as efﬁciently as possible. In the second level

control unit SGD, the local system stability is main-

tained by allowing power transmission among SGAs.

The task for the SGD is to guarantee the satisfac-

tion of all user demands, maintain the system stabil-

ity and minimize the transmission losses considering

the local grid topology and network condition. The

optimization problem is constructed based on a busi-

ness inspired model and the objective function varies

due to different scenarios and requirements. However,

there are some basic principles about the optimization

model construction:

• SGD Optimization. On a grid level, the SGD opti-

mization collects information from the SGAs con-

stituting the SoftGrid, including battery SoC and

a cumulated energy consumption/generation pre-

diction over a time-discrete prognosis horizon. It

is assumed that the network topology in the Soft-

Grid is known (as it is constructed from scratch)

and therefore one can compute the admittance ma-

trix to incorporate the signiﬁcant cable losses in

the low voltage DC SoftGrid. The SGD opti-

mization now computes for each single SGA and

each interval of the time-discrete prognosis hori-

zon optimal power inﬂows or outﬂows into the

SoftGrid, taking into account transmissions losses

and moreover additional generation capacities in

the SGAs like diesel generators that the SGAs can

dispatch in the case of necessity. Here, optimality

means that power demands are met, diesel gener-

ator costs are avoided, batteries are charged, and

resistive cable losses are minimized, as good as

possible. Finally, the SGD is a purely continu-

ous optimization problem and can be solved efﬁ-

ciently.

• SGA Optimization. The optimization on the local

level guides the consumers connected to the SGA,

its generators and monitors the battery SoC. More

precisely, over the same time discrete prognosis

SMARTGREENS2013-2ndInternationalConferenceonSmartGridsandGreenITSystems

horizon the SGD uses the SGA optimization com-

putes for each of its connected consumers as well

as for the generators it can control (e.g. a diesel

generator, opposed to a photovoltaic panel that

generates power according to solar irradiance) a

control signal, while it has to satisfy the power

inﬂow/outﬂow the SGD imposes on the single

SGA. The nature of these control signals depend

on the nature of the consumers and generators.

For deferrable loads with a ﬁxed operation pat-

tern, binary signals decide about whether the load

is turned on or off in a certain used-deﬁned time

window of the time-discrete prognosis horizon.

For energy-control loads and controllable gener-

ators a binary variable controls whether the ma-

chine is turned on or off during a certain user-

deﬁned time window of the prognosis horizon,

while a continuous variable decides about the

power with which the machine shall run (tak-

ing into account the machine’s technical opera-

tion range). For proﬁle-type loads, a continuous

variable decides about dimming (again within the

loads technical limits) while in case of insufﬁcient

power supply or a low battery a binary variable

may switch the proﬁle load off in every time in-

terval. Also, consumers may be associated a pri-

ority such that the demands of high priority con-

sumers are satisﬁed prior to those of low prior-

ity, which may in extreme cases be completely

switched off by the optimization. When neglect-

ing transmission losses between the SGA and its

connected components (which are spatially close

to the SGA), the resulting optimization problem

has the form of a mixed integer linear program

(MILP), which can be solved efﬁciently on an em-

bedded computer even for realistic problem di-

mension.

In the end, we are able to separate the two opti-

mization problems to two categories: The SGA op-

timization is modeled as a mixed integer linear pro-

gramming (MILP) problem, which is solved by the

CBC solver (CBC, 2012). The SGD optimization

is modeled as a nonlinear programming (NLP) prob-

lem, which is solved by the Ipopt solver (Ipopt, 2012).

This split into a purely continuous optimization model

for the SGD and a mixed integer linear program for

the SGA has several advantages. Firstly, it avoids

solving a large mixed-integer nonlinear program that

otherwise would guide all consumers and generators

in the entire SoftGrid including the SGAs and their

components. Moreover, since the optimal guidance

for an SGA’s components is done locally, i.e. solved

on the SGA’s embedded hardware, the system is more

robust towards failure in the computation or in the

computing hardware: even if the dispatcher or a sin-

gle SGA fails to deliver results, the other problems

may still be solved independently.

5 SIMULATION RESULTS

In order to verify the concept and ﬁnd out appropriate

system conﬁguration parameters, different scenarios

have been tested. Fig. 7 shows the stand-alone mode

of a single SGA. This example shows a household

with typical home appliances like television, refriger-

ator and washing machine. In this case, the refrigera-

tor is a ﬁxed-proﬁle consumer, which needs to operate

all time, while the washing machine is a deferrable

consumer, which can be scheduled to operate in an

appropriate time window to gain certain ﬂexibility.

The operation of LED and television are simulated by

stochastic time series, and the expectations are passed

to the optimization model as prognoses. Fig. 8 shows

the electrical appliances’ behavior for one day. It can

be seen that the SGA can satisfy the user demand by

allocate the power properly. Under the guidance of

the optimization in the SGA, the washing machine is

turned on at noon, when the electricity supply is sufﬁ-

cient due to the high solar irradiance thus large photo-

voltaic power generation and electricity consumption

peak has not arrived yet. In order to check the robust-

ness of the optimization model, a series of tests are

carried out using different time series. In our tests,

the optimization algorithm shows very good perfor-

mance to keep the user demands satisﬁed. Only in

very few occasions, some LEDs are dimmed in order

to save energy.

Figure 7: Test Scenario 1: Stand-alone SGA with Fixed-

proﬁle and Time-deferrable Consumers.

As introduced in Section 2, SoftGrid has two-level

control architecture. Fig. 9 shows an example with

three SGAs and one SGD. In this case, no external

SoftGrid:AGreenFieldApproachofFutureSmartGrid

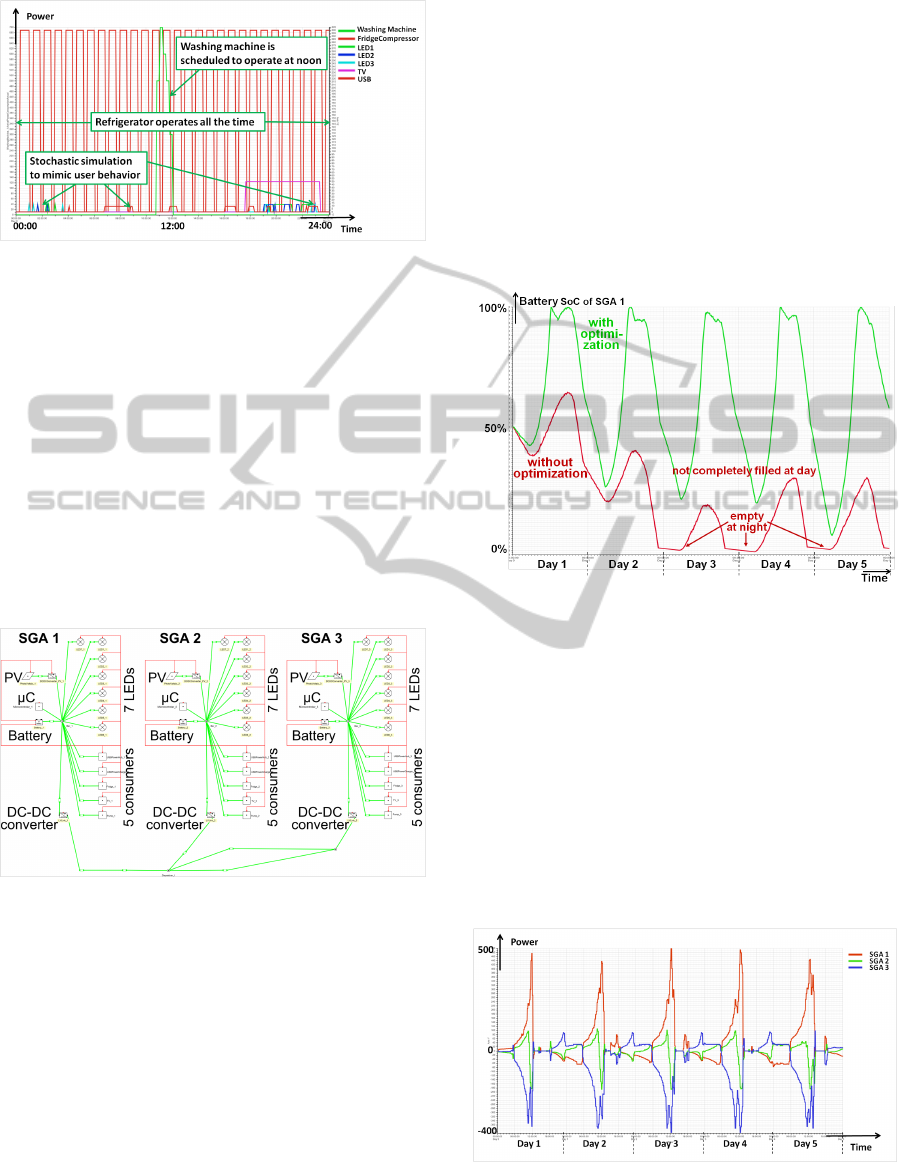
Figure 8: Power Consumption of Consumers.

grid is provided. This example is to test the perfor-

mance of a SGD optimization algorithm. Each lo-

cal grid controlled by the SGA contains one battery,

one photovoltaic panel and several consumers. This

system performance depends strongly on the local

weather condition. Besides, we also investigate the

system in a special condition. In the ﬁrst SGA, we set

up a battery with big capacity and a photovoltaic with

low power production ability. In the second SGA,

both parameters of battery and photovoltaic capacity

are chosen to be medium. In the third SGA, we use a

battery with a small capacity and a photovoltaic with

high peak power generation. The optimization in the

SGD has to balance this uneven system conﬁguration.

Figure 9: Test Scenario 2: 3 SGAs and 1 SGD.

Since there is no deferrable load and no biomass

generator in the local grid, the SGA has little freedom

in optimization. Without the SGD optimization, the

SGA has troubles to run in the stand-alone mode. Ob-

viously, the battery can only get charged at daytime.

Even if the ﬁrst battery has sufﬁcient initial level, it

does not get enough reﬁlls due to the small photo-

voltaic panel in the local system. Therefore, the user

demands in the following days cannot be fulﬁlled. On

the other side, the third battery is too small to store

the energy generated by the photovoltaic during the

daytime, which causes resource waste. The optimiza-

tion algorithm running in the SGD allows power ﬂow

among the neighboring SGAs. It can balance the sup-

ply and demand globally. Fig. 10 shows the compari-

son of battery status with and without SGD optimiza-

tion. We see that during the daytime extra energy gen-

erated by the third photovoltaic panel is transmitted

to the ﬁrst battery, while in the night the third SGA

with small battery gets support from the ﬁrst SGA

to fulﬁll the user demands. In such a way, the three

SGAs can balance the supply and demand by support-

ing each other. Fig. 11 shows the power transmission

among SGAs, the positive power ﬂow means that a

local SGA receives power while the negative power

ﬂow means a local SGA exports power.

Figure 10: Comparison of Battery Status with and without

Optimization.

This example proves that the two-level control ar-

chitecture is very reliable. The SGD optimization

can balance the demand and supply even under ex-

treme situations. Nevertheless, this situation should

be avoided in the praxis, since power transmission

among SGAs will cause power loss. The guideline

for SoftGrid is to generate and consume power lo-

cally. Power transmission among SGAs is for mutual

support only. With the help of our simulation system,

system design ﬂaws like the above example can be

detected in the early stage.

Figure 11: Power Transmission among SGAs.

SMARTGREENS2013-2ndInternationalConferenceonSmartGridsandGreenITSystems

6 CONCLUSIONS AND FUTURE

WORK

In this paper, the concept of SoftGrid as a green ﬁeld

approach for smart grid is presented. It is a power

ﬂow optimization and optimal scheduling based de-

centralized power system, which adopts the two-level

control architecture. This two-level control architec-

ture can build up a local grid from scratch and inte-

grate the local grid to any existing power grid. The

concept of SoftGrid is veriﬁed through system mod-

eling and simulation. The ﬂexible simulation soft-

ware allows user to design systems with different net-

work topology and test system designs under different

scenarios. The simulation results show that SoftGrid

combines the advantages of smart grid and microgrid,

providing a power grid solution with both ﬂexibility

and reliability. It stands for the power grid devel-

opment trend in the future. The optimization mod-

els in SGA and SGD can be adapted to meet differ-

ent user needs. In general, the SGA optimization is

a MILP Problem solved by the CBC solver and the

SGD optimization is a NLP problem solved by the

Ipopt solver. This separation avoids the difﬁculty of

solving a MINLP problem and thus allow the prob-

lems to be solved on an embedded computer. The

details of optimization models will be explained in

future publications. The hardware realization of this

concept is now under test.

ACKNOWLEDGEMENTS

The project is initiated by Dr. Rainer Speh and car-

ried out in cooperation with several research groups

of Siemens AG Corporate Technology: CT RTC POA

POE-DE and CT RTC NEC EMB-DE, who take re-

sponsibility of hardware implementation and commu-

nication. The colleagues Dr. Richard Kuntschke, Dr.

Michal-Wolfgang Waszak, and Dr. J

org Heuer also

have contributed to this paper.

REFERENCES

Appelbaum, J. and Weiss, R. (1982). An electrical model of

the lead-acid battery. In Telecommunications Energy

Conference, pages 304–307.

CBC (2012). Coin-or branch and cut. https://projects.coin-

or.org/Cbc.

COIN-OR (2012). Computational infrastructure for opera-

tions research. http://www.coin-or.org.

Dodrill, K. (2010). Understanding the beneﬁts of

the smart grid. http://www.netl.doe.gov/smartgrid/

referenceshelf/whitepapers/06.18.2010 Understanding

%20Smart%20 Grid%20Beneﬁts.pdf.

Gonzalez-Longatt, F. M. (2006). Model of photovoltaic

module in matlab. In II CIBELEC 2006.

Ipopt (2012). Interior point optimizer. https://projects.coin-

or.org/Ipopt.

Jurado, F., Cano, A., and Carpio, J. (2003). Modelling of

combined cycle power plants using biomass. Renew-

able Energy, 28:743–753.

Lasseter, R. H. and Mettam, P. P. (2004). Microgrid: A

conceptual solution. In Power Electronics Specialists

Conference, volume 6, pages 4085–4290.

Mohamed, F. A. (2008). Microgrid modelling and on-

line management. PhD thesis, Helsinki University of

Technology.

Salameh, Z. M., Casacca, M. A., and Lynch, W. (March

1992). A mathematical model for lead-acid batteries.

IEEE Transactions on Energy Conversions, 7(1):93–

97.

Siemens (2012). http://w3.siemens.com/smartgrid/global/

en/pages/default.aspx.

Tesla, N. (1888). A New System of Alternating Current Mo-

tors and Transformers. American Institute of Electri-

cal Engineers.

SoftGrid:AGreenFieldApproachofFutureSmartGrid