Contribution of Probabilistic Grammar Inference with k-Testable

Language for Knowledge Modeling

Application on Aging People

Catherine Combes

1,2

and Jean Azéma

University of Lyon, Bron, France

Hubert CURIEN Laboratoy, UMR CNRS 5516, University of Jean Monnet,18 Rue Benoît Lauras,

42023 Saint-Etienne cedex 2, France

University of Jean Monnet, 23 Avenue du Docteur Paul Michelon, 42023 Saint-Etienne cedex 2, France

Keywords: Grammar Inference, k-Testable Language in Strict Sense, Probabilistic Deterministic Finite Automata, Time

Series, Evolution of Elderly People Disability.

Abstract: We investigate the contribution of unsupervised learning and regular grammatical inference to respectively

identify profiles of elderly people and their development over time in order to evaluate care needs (human,

financial and physical resources). The proposed approach is based on k-Testable Languages in the Strict

Sense Inference algorithm in order to infer a probabilistic automaton from which a Markovian model which

has a discrete (finite or countable) state-space has been deduced. In simulating the corresponding Markov

chain model, it is possible to obtain information on population ageing. We have verified if our observed

system conforms to a unique long term state vector, called the stationary distribution and the steady-state.

1 INTRODUCTION

Demographic shifts in the population and the fact

that people are living longer have created an

awareness that the health care system is and will be

increasingly difficult to control, organize and

finance especially where the ageing population are

concerned. The senior citizen population is

increasing along with the diversity of their health

backgrounds and medico-social needs which cannot

be provided easily because of health aspects, social

conventions and lifestyles that are intertwined with

the ageing process. Long-term care is a variety of

services that includes medical and non-medical care

to people who have a chronic illness or disability.

This illness or disability could include a problem

with memory loss, confusion, or disorientation. This

is called cognitive impairment and can result from

conditions such as Alzheimer’s disease. Care needs

often progress as age or as chronic illness or

disability progresses. Long-term care helps meet

health or personal needs. Most long-term care is to

assist people with support services such as activities

of daily living like dressing, bathing, and using the

toilet. Approximately 70% of individuals over the

age of 65 will require at least some type of long-

term care services during their lifetime. Over 40%

will need care in a nursing home for some period of

time. Nursing homes provide long-term care to

people who need more extensive care, particularly

those whose needs include nursing care or 24-hour

supervision in addition to their personal care needs.

We focus our interest on nursing homes. This project

is being carried out in close collaboration with a

French mutual benefit organization called

“Mutualité Française de la Loire” which manages

several nursing homes. The steps of the project

consist in:

1. The specification of elderly people profiles in

using unsupervised learning approach (Combes

and Azéma, 2013),

2. The study of the development of these profiles

over time in using a probabilistic graph of

transitions between the clusters inferred by k-

TSSI (k-Testable Languages in the Strict Sense

Inference) algorithm. The objective is to deduce

Markov process which has a discrete (finite or

countable) state-space.

3. Discrete-time Markov chain simulation is used

to forecast population ageing. It allows to

identify the elderly people care needs and the

451

Combes C. and Azéma J..

Contribution of Probabilistic Grammar Inference with k-Testable Language for Knowledge Modeling - Application on Aging People.

DOI: 10.5220/0004356804510460

In Proceedings of the 5th International Conference on Agents and Artiﬁcial Intelligence (LAFLang-2013), pages 451-460

ISBN: 978-989-8565-38-9

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

workload in short-term, medium-term and long-

term and to predict the future costs. An

application is presented in (Combes et al.,

2008).

This presentation is split up into seven sections.

After an introduction describing the scope of the

study, we introduce the characteristics of the

collected data in section 2. In section 3, we describe

the profiles of residents obtained in using cluster

analysis. A brief review of previous works is

presented in section 4. The section 5 treats the

techniques used (regular probabilistic grammar

inference) to model the automaton symbolizing the

changing profiles and their development over time.

Starting from this automaton, a Markov model is

deduced. Thereby, it is possible to verify if our

system is achieving a steady state. The section 6

presents the obtained results concerning the four

medical nursing homes (called Bernadette, Soleil,

Les Myosotis, Val Dorlay situated in France) and

dementia disease and more particular, Alzheimer’s

disease. We conclude with some perspectives.

2 DATA COLLECTED

The quantitative data arises from the databases and

the corresponding information system deals with the

evaluation of autonomy/disability of elderly people.

Dependence evaluation in France is carried out using

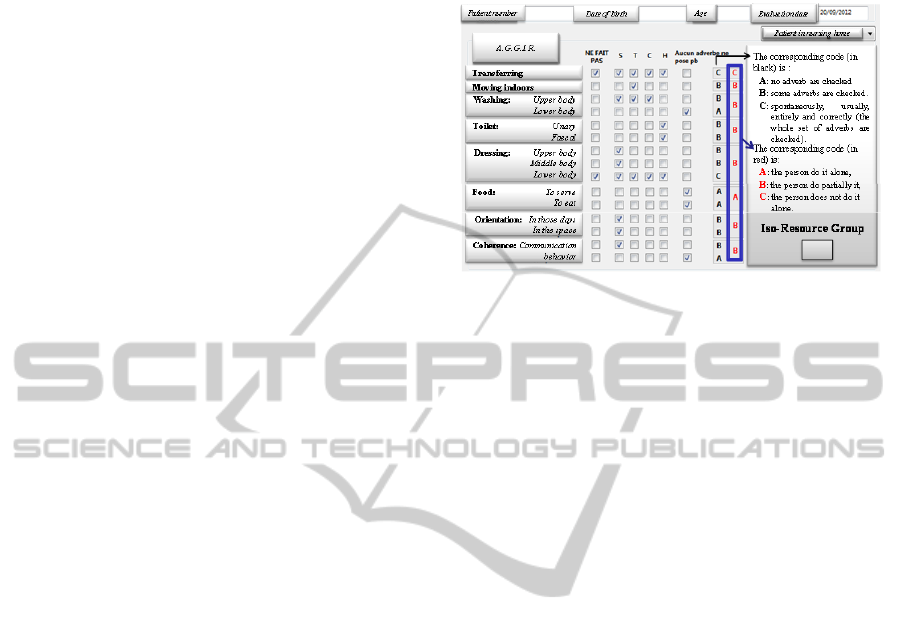
a specific national scale called AGGIR: Autonomy-

Gerontology-Group-Iso-Resources. The quantitative

data concerns 628 residents and more than 2,200

observations of independence evaluations. The

evaluations are made by the resident doctor in

collaboration with the medical staff. An item can be

evaluated using the four adverbs (see figure 1):

 Spontaneously corresponding to the letter S,

 Entirely corresponding to the letter T,

 Correctly corresponding to the letter C,

 Usually corresponding to the letter H.

The codification is the following. If all four

adverbs are marked, the code is C. If less than four

adverbs are checked (three or two or one), the code

is B. If no adverb is checked, the code is A.

The proposed algorithm uses numerical data. So,

the corresponding values are:

 0 for code A meaning the person can do it

alone,

 1 for code B meaning the person can do

partially it,



2 for code C meaning the person cannot do it

alone.

The first step is to analyze the degree of

autonomy-disability in order to identify clusters.

Figure 1: A.G.G.I.R scale.

3 IDENTIFICATION OF

RESIDENTS’ PROFILES

The aim is to find feature-patterns related to the

autonomy-disability level of elderly people living in

nursing homes. These levels correspond to profiles

based on the people’s ability to perform activities of

daily living like being able to wash, dress and move.

To achieve this aim, an unsupervised learning

approach is proposed (Combes and Azéma, 2013). It

based on principal component analysis technique to

direct the determination of the clusters with self-

organizing partitions. Cluster analysis is made on the

8 variables: Transferring to or from bed or chair,

Moving indoors, Washing, Toilet, Dressing, Food,

Orientation, Coherence. The cluster analysis

identifies two kinds of patterns:

 The decline in executive functions regarding to

motor and functional abilities called apraxia

disorders,

 The cognitive impairment and

neuropsychological deficits.

By combining clustering with a machine learning

process, we could be able to predict the development

of physical autonomy loss or mental autonomy loss

in elderly people over time. To reach this objective,

we use machine learning approach based on

grammar inference in order to infer a probabilistic

automaton. In the article, we only present the

patients’ profiles evolution regarding to upper

function disorders (cognitive impairment).

4 RELATED WORKS

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

452

We want to obtain a probabilistic graph of

transitions between states (clusters) with the length-

of-stay in each state (temporal state representations).

It is also interesting to study cluster succession of

length k (for example, the 3 last states of resident’s

clusters, a k timed series). Probabilistic automata are

used in various areas in pattern recognition or in

fields to which pattern recognition is linked.

Different concept learning algorithms have been

developed for different types of concepts. The

learning of deterministic finite automata (DFA), also

called regular inference is based on acceptance of

regular languages which allow to model the

behaviour of systems. The aim consists in

constructing a DFA from information about the set

of words it accepts. There are many algorithms for

regular inference (Angluin, 1987); (Garcia and

Vidal, 1990a); (Rivest and Sphapire, 1993); (Balczar

et al., 1997); (Parekh et al., 1998); (Parekh and

Honavar, 2001); (Bugalho and Oliviera, 2005)...

A finite automaton with transition probabilities

represents a distribution over the set of all strings

defined over a finite alphabet. The articles presented

by (Rico-Juan et al., 2000) and (Vidal et al., 2005)

present a survey and a study of the relations and

properties of probabilistic finite-automata and tree.

(Dupont et al., 2005) clarify the links between

probabilistic automata and hidden Markov models.

In a first part of this work, the authors present:

 the probabilities distributions generated by

these models,

 the necessary and sufficient conditions for an

automaton to define a probabilistic language.

The authors show that one the one hand,

probabilistic deterministic finite automata (PDFA)

form a proper subclass of probabilistic non-

deterministic automata (PNFA) and the other hand,

PNFA and hidden Markov models are equivalent.

We assume that our problem could be modelled

as a state transition graph (probabilistic deterministic

finite automaton). Consequently, the pattern

recognition of sequences and the corresponding

probabilities could be inductively learned via an

inference algorithm. The k-TSSI (k-Testable

Languages in the Strict Sense Inference) algorithm

(Garcia et al., 1990a, 1990b) could be useful,

convenient and suitable for two reasons: the

simplicity of implementation and the possibility to

take into account memory effects (timed macro-

states). The inductive inference of the class of k –

testable languages in the strict sense (k-TLSS) has

been studied and adapted to local languages, N-

grams and tree languages. A k-TLSS is essentially

defined by a finite set of substrings of length k that

are permitted to appear in the strings of then

language. Given a size k of memory, the objective is

to find an automaton for the language. This subclass

of language called k-testable language has the

property that the next character is only dependent on

the previous k-1 characters. In our case, it is

interesting to be able to identify the substrings

(memory) of length k. But, our goal is to infer a

timed model and an automaton inferred by the k-

TSSI algorithm does not take into account the timed-

state. The interesting question is how to infer timed

automata and very few works exist in the domain

(Alur et al., 1990, 1991); (Alur and Dill, 1994);

(Grinchtein et al., 2005); (Verwer et al., 2007,

2011). Timed automata correspond to finite state

models where explicit notion of time is taken into

account and is represented by timed events. Time

can be modelled in different ways, e.g. discrete or

continuous. The more recent works (Verwer et al.,

2007, 2011) propose an algorithm for learning

simple timed automata, known as real-time automata

where the transitions of real-time automata can have

a temporal constraint on the time of occurrence of

the current symbol relative to the previous symbol.

The problem is also that it is difficult to take into

account a set of substrings of length k (k>1) and the

algorithm is not generalized to probabilistic timed-

automata. In this section we propose a model in

order to take into account the concept of time in the

automaton inferred by the k-TSSI algorithm (i.e. the

duration of time a resident spends in a particular

cluster). In the next section, we present the

implementation of the model.

5 DEVELOPMENT OF

PATIENTS’ PROFILES:

MODEL IMPLEMENTATION

The method consists in:

1. Learning a deterministic finite automata (DFA)

using k-TSSI algorithm.

2. Transforming this DFA into a probabilistic

DFA.

3. Converting this probabilistic DFA in a Markov

chain model.

5.1 Preliminaries

The aim of grammatical inference is to learn models

of languages from examples of sentences of these

languages. Sentences can be any structured

composition of primitive elements or symbols,

ContributionofProbabilisticGrammarInferencewithk-TestableLanguageforKnowledgeModeling-Applicationon

AgingPeople

453

though the most common type of composition is the

concatenation. So we infer a grammar and the

corresponding representation is an automaton.

An automaton consists of:

- : a finite input alphabet of symbols,

- *: the set of all finite length strings generated

from ,

- L: a sub-set of * corresponding to the

collected words,

- Q: a finite set of states with q

as start state, F

is a set of final states (F  Q),

- : a transition function of

QQ. So that q’=

(q,



) returns a state for current state q and

input symbol



from . Each transition is noted

by 3-tuple (q,



,q’).

A finite automaton is a 5-tuple (Q, , ,q

,F). If

for all q  Q and for all



 , (q,



) corresponds

to a unique state of Q, then the automaton is said to

be a Deterministic Finite Automaton (DFA).

Grammatical inference refers to the process of

learning rules from a set of labelled examples. It

belongs to a class of inductive inference problems

(Angluin and Smith, 1983) in which the target

domain is a formal language (a set of strings

generated from some alphabet ) and the hypothesis

space is a family of grammars. It is also often

referred to as automata induction, grammar

induction, or automatic language acquisition. The

inference process aims at finding a minimum

automaton (the canonical automaton) that is

compatible with the examples. In regular grammar

inference, we have a finite alphabet  and a regular

language L  *. Given a set of examples that are in

the language (I

) and a (possibly empty) set of

examples not in the language (I

), the task is to infer

a deterministic finite automaton A that accepts the

examples in I

and rejects the examples in I

5.2 k-TSS Inference Algorithm

The k-TSSI algorithm (Garcia and Vidal, 1990a)

allows us to infer k-Testable Languages in the Strict

Sense. The inductive inference of the class of k-

Testable Languages in the Strict Sense is defined by

a finite set of substrings of length k that are allowed

to appear in the strings of the language. Given a

positive sample I

 L of strings of an unknown

language, a deterministic finite-state automaton that

recognizes the smallest k-TLSS containing I

obtained. An automaton inferred by the k-TSSI

algorithm is by its construction, non-ambiguous.

Moreover, our choice is justified by the fact that k-

testable (k > 1) can take into account a memory

effect (ie N-gram). Indeed, we observed during data

analysis that the change in evolution of the

autonomy/disability state depends on the previous

resident’s states and their diseases (especially for

chronic and disabling diseases such as osteoarticular

degenerative diseases, anxio-depressive disorder,

behavioural disorders…). To illustrate our approach

and for the sake of simplicity, we will present in this

article, the results obtained with 1-TSSL (the next

state depends only on the previous states) in order to

explain how we turn the time series into sequences.

We choose to divide up the length-of-stay in the

each cluster (for example, one discrete step = 30

days). Consequently, the corresponding automaton is

a 6-tuple (Q,





,F,d) where d corresponds to the

length-of-stay in the states. In the following sections,

we explain the implementation of the model through

an example (on only six residents: 7, 12, 17, 14, 8,

44 corresponding to an excerpt of the collected

data).

5.2.1 Setting Up the Alphabet

The assessment of elderly people’s

autonomy/disability allows us to classify residents

into five levels of mental dependence situation (5 to

1 in decreasing order of severity). Figure 2 presents

the data collected from the database.

Figure 2: Data and sequences.

The resident assessment is made on different

dates. For example, resident number 7 was evaluated

at level 3 (mental disorder) on the 06/24/2002. For

all the assessments concerning resident number 7,

we can deduce the sequence: 3321111. But this

sequence does not express the amount of time the

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

454

person spends in each state (level of mental

disorder).

5.2.2 Preliminary Mapping of the Set of

Strings (k-TSSI Algorithm)

The objective is to obtain a stochastic state transition

graph taking into account the length-of-stay in each

state.

The first step consists in the definition of the

alphabet (the set ). The set  is based on an

alphabet of 6 symbols - {a,b,c,d,e,f} which

correspond to:

- a length-of-stay in cluster number 1 during a

given period (example:30 days),

- b length-of-stay in cluster number 2 during a

given period,

- etc (until the symbol e for cluster number 5).

The symbol f models the fact that a resident can

leave the nursing home or corresponds to the last

resident assessment during the last 30 days before

the data extraction. It is only used when we want to

deduce the Markov model. Consequently, in the

following example, the symbol f does not exist in

figure 3.

The second step concerns the identification of

the words which corresponds to the translation of the

initial sequence in order to take into account length

of time spent in each cluster. Resident number 7

stayed in cluster number 3 from 06/24/2002 to

03/15/2004 (date at which the resident was evaluated

and changed to cluster number 2). Thus resident

number 7 stayed in cluster number 3 for about 22

periods of 30 days. The symbol modeling cluster

number 3 for 30 days is c, consequently the initial

sequence “33” becomes “cccccccccccccccccccccc”.

The resident stayed in cluster number 2 for 9

periods… and the corresponding word is:

ccccccccccccccccccccccbbbbbbbbbaaaaaaaaaa

aaaaaaaa

So we obtain the set L  *. L corresponds to

the learning set from which the automaton is

inferred. The initial set of sequences (figure 2)

{3321111, 42, 212, 56656, 243333, 4

}

becomes:

L={ccccccccccccccccccccccbbbbbbbbbaaaaaaa

aaaaaaaaaaa, ddb, bbbbbaaaab, ddddeeeeeeeeddee,

bbbdddddddccccccccccccccccc, dd}

From the set L in using k-TSSI algorithm (to

simplify, we present the case corresponding to k=1),

we obtain the automaton described in figure 3. This

algorithm consists in building the sets Q, , ,q

by observation of the corresponding events in the

training strings. From these sets, a finite-state

automaton that recognizes the associated language is

straightforwardly built. The detail of the algorithm is

described in (Garcia et al., 1990b).

Figure 3: The automaton inferred by the algorithm k-TSSI

with q

=0.

5.3 Computation of Probabilities

The automaton is inferred by the k-TSSI algorithm.

We have to associate transition probabilities with

states. In order to compute these probabilities, we

use the learning set L. From the words of set L,

when they are recognized by the automaton inferred

by k-TSSI, we count:

- The transition between two states for a given

symbol (transition from the state q by the

symbol



): cp



(q,



)

- each transition in a state q: cp

- if a state q is the final state (end of the words):

q_final

For the algorithm, we use the three epochs-

counts in order to estimate the probabilities. The

algorithm computing the probabilities from a

learning set is the following.

Input I

= {

,…,x

I+

} //collected sample

= (Q, , ,q

,F) //the inferred automaton

Output PA

= { p



( q,xij)

, p

q_final

} //the obtained

probabilities

Begin

For i=1 until I

 //for all words x

in I

q q

For j=1 until x

 //for all symbol x

of the word



q’ 



( q,x

)

//the corresponding transition

++ //epoch-count in passing state



( q,xij)

++ //epoch-count in passing

transition

q q’

EndFor

q_final

++ //epoch-count concerning the

final states

ContributionofProbabilisticGrammarInferencewithk-TestableLanguageforKnowledgeModeling-Applicationon

AgingPeople

455

EndFor

For all q  Q

q_final

= cp

q_final

/ cp

//Computation of final-state

probabilities

EndFor

For all



( q,



)



( q,



)

= cp



( q,



)

/ cp

//Computation of transition

probabilities

EndFor

Return PA

The obtained results from the sample presented in

figure 2 are:

 cp

= (6

(0)

, 39

(1)

, 19

(2)

, 22

(3)

, 17

(4)

, 10

(5)

 cp

q_final

= (0

(0)

, 1

(1)

, 2

(2)

, 1

(3)

, 1

(4)

, 1

(5)

 cp



(q,



)

= (2



(0,b)

, 1



(0,c)

, 3



(0,d)

, 0



(0,e)



(1,b)

, 37



(1,c)

, 2



(2,a)

, 14



(2,b)

, 1



(2,d)



(3,a)

, 1



(3,b)

, 1



(4,b)

, 1



(4,c)

, 12



(4,d)



(4,e),



(5,d),



(5,e)

And afterwards, we deduce the probabilities:

 p

q_final

= (0/6

(0)

, 1/39

(1)

, 2/19

(2)

, 1/22

(3)

1/17

(4)

, 1/10

(5)

 p



(q,



)

= (2/6



(0,b)

, 1/6



(0,c)

, 3/6



(0,d)

1/39



(1,b)

, 37/39



(1,c)

, 2/19



(2,a)

14/19



(2,b)

, 1/19



(2,d)

, 20/22



(3,a)

1/22



(3,b)

,1/17



(4,b)

, 1/17



(4,c)

, 12/17



(4,d)

2/17



(4,e)

, 1/10



(5,d)

, 8/10



(5,e)

So we obtain the probabilistic deterministic

automaton where the time series are taken into

account. The advantage of using 1-TSSL (k-TSSI

algorithm with k=1) lies in the fact that one state

corresponds to one symbol. We have added a new

symbol f and a final state q

in order to facilitate the

translation of the probabilistic automaton into a

Markov process. For all q states where p

q_final

>0,

we add a transition



(q,g)= q

, p



(q,g)

= p

q_final

and

q_final

0. We note that p

_final

=1.

From patients’ file living in Soleil nursing home

and suffering from Alzheimer disease, the

probability matrix of transitions between states and

the corresponding automaton are respectively

presented in the table 1 and in the figure 4.

Table 1: The corresponding probability matrix of

transitions between states (figure 4).

To 

From 

Cluster 5 Cluster4 Cluster3 Cluster2 Cluster1

0.5072 0.0580 0.3333 0.0290 0.0725

luste

5 0.9738 0.0005 0.0009 0 0 0.0248

luste

4 0.0629 0.9021 0.0210 0 0 0.0140

luste

3 0.0229 0.0134 0.9408 0.0019 0.0019 0.0191

luste

2 0 0.0299 0.0299 0.8955 0 0.0448

luste

1 0 0 0.0122 0.0488 0.9268 0.0122

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

456

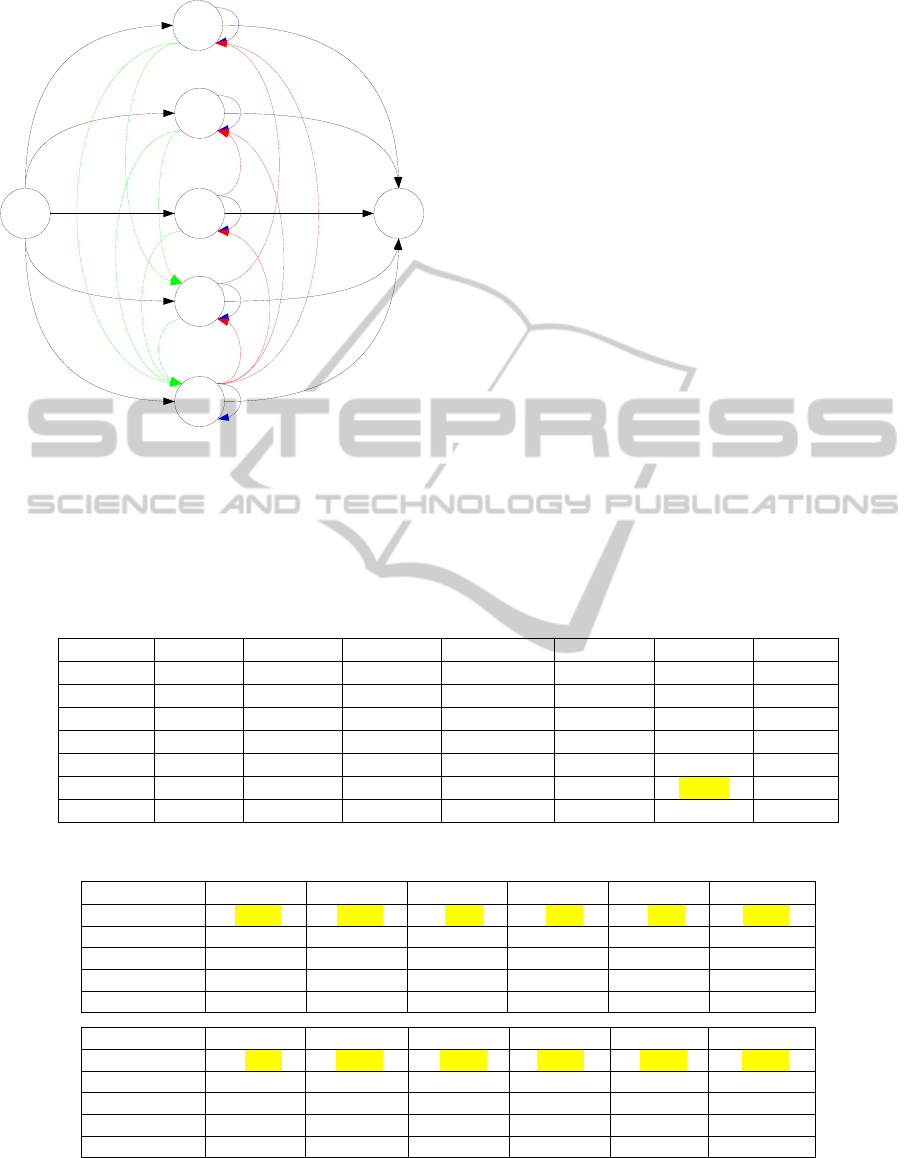
Figure 4: The automaton inferred by the algorithm k-TSSL

(Soleil nursing home: residents suffering from dementia).

5.4 Markov Model

The final state q

not only represents the resident

state when they left the system but also the last

resident assessment (resident present in the system at

the date of database extraction).

In order to obtain the Markov chain model, we

have to compute the probabilities:

- P

: Input probabilities (i.e. the initial resident

assessments) in each cluster

(i=1..5),

- Psi: Output probabilities (i.e. the last resident

assessments when residents leave the system)

in being cluster

(i=1..5) after 30 days

(corresponding to the equidistant discrete

time).

We have also to modify the probabilities of

staying in cluster

(i=1..5), regarding if the patient is

staying in the nursing home at the at the date of

database extraction (these evaluations are taken into

account in the transition with the symbol f to q

table 1). We add the number of evaluations in the

corresponding cluster

. It is the reason that the

probability to be in cluster1, (initially is 0.9738 in

table1) becomes 0.9902 in the Markov matrix.

When a resident leaves the system, he is

immediately replaced by a new resident.

Consequently, two other probabilities are taken into

account PE and PS. The Markov matrix is presented

in the table 2.

Table 2: The Markov matrix obtained from the collected data - Soleil Nursing home: patient suffering from dementia.

Cluster5 Cluster4 Cluster3 Cluster2 Cluster1 PSS

PEE 0 0 0 0 0 0 1

Cluster5 0.0725 0.9390 0 0.0019 0 0 0

Cluster4 0.0290 0.0488 0.9403 0.0019 0 0 0

Cluster3 0.3333 0.0122 0.0299 0.9580 0.0210 0.0009 0

Cluster2 0.0580 0 0.0299 0.0134 0.9161 0.0005 0

Cluster1 0.5072 0 0 0.0229 0.0629 0.9902 0

Psi 0 0 0 0.0019 0 0.0084 0

Table 4: Evolution of patients’ profiles in 2 years.

No Dementia Cluster5 Cluster4 Cluster3 Cluster2 Cluster1 Exit

Cluster5 50.9% 16.0% 5.8% 1.6% 2.4% 23.3%

Cluster4 3.8% 56.0% 10.6% 3.4% 4.1% 22.2%

Cluster3 4.3% 4.0% 25.2% 9.1% 13.8% 43.6%

Cluster2 0.8% 0.9% 11.4% 29.4% 29.6% 27.9%

Cluster1 0.1% 0.6% 0.7% 1.3% 33.1% 64.2%

Dementia

Cluster5 Cluster4 Cluster3 Cluster2 Cluster1

Exit

Cluster5 9.7% 20.6% 27.1% 12.7% 19.4% 10.5%

Cluster4 0.5% 20.2% 32.4% 14.7% 20.0% 12.2%

Cluster3 0.6% 1.5% 21.8% 17.7% 34.1% 24.3%

Cluster2 0.1% 0.1% 1.9% 11.9% 31.7% 54.3%

Cluster1 0.2% 0.1% 1.5% 15.5% 64.8% 17.9%

Cluster

c c

ContributionofProbabilisticGrammarInferencewithk-TestableLanguageforKnowledgeModeling-Applicationon

AgingPeople

457

We verify if the system reaches a steady state. Out

of definition, an eigenvector x is associated to

eigenvalue l if: A*x =l*x

(A corresponding to the probabilities matrix

presented in table 2)

If an eigenvector of x is associated to a unique

eigenvalue 1, such a vector is called a steady state

vector. If we identify only one eigenvalue 1, then the

distribution is said to be irreducible and aperiodic.

The eigenvector associated with the eigenvalue 1

has been computed. We have one eigenvalue 1 and

the corresponding eigenvector x is the following:

0.00692 0.01263 0.01966 0.12108 0.03768 0.79510

0.00693

The interpretation of this eigenvector is that the

system (ratio of the resident profiles without 0.69%

of resident turnover of input/output in the nursing

home) evolves towards a state where the percentages

of population are:

- 1.28% are in cluster5,

- 1.99% are in cluster4,

- 12.28% are in cluster3,

- 3.82% are in cluster2,

- 80.63% are in cluster1.

6 EXPERIMENTS

The table 3 presents the steady state vectors from

different samples. We see that the decline is more

important for elderly people with dementia than non-

demented elderly people.

Table 3: Steady state: population staying in medical

nursing homes.

4 Nursing

Homes

Patient Without

Dementia

Disease

Patient

Suffering from

Dementia

Cluster5 3.57% 35.98% 0.32%

Cluster4 13.42% 27.00% 1.93%

Cluster3 27.80% 15.96% 5.21%

Cluster2 11.54% 5.65% 6.84%

Cluster1 43.66% 15.40% 85.69%

Now, we simulate the evolution over time in

using transition matrix used to model the Markov

chain concerning each population. The results

concerning the patients’ profiles in 2 years are

presented in table 4.

If the patient does not suffer from dementia

disease, if he is initially in cluster5, the probabilities

that the patient will be staying in:

 Cluster5 is 50.9%,

 Custer4 is 16%,

 Cluster3 is 5.8% ...

and leaves the system with a probability near to

23%.

If the patient suffers of dementia, the

probabilities that the patient which will be staying

in:

 Cluster5 is 9.7%,

 Cluster4 is 20.6%,

 Cluster3 is 27.1%, ...

and leaves the system with a probability near to

10%.

7 CONCLUSIONS

An application of grammatical inference to the

identification of the resident’s autonomy-disability

progress over time has been presented. From profiles

identified in using clustering approach (Combes and

Azéma, 2013), we propose preliminary results of an

investigation where regular grammars are used for

modeling the ageing people evolution over time. The

finite automaton is inferred in using the k-TSSI

algorithm and afterward modified in order to obtain

a probabilistic graph of transitions between states

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

458

(clusters) with the length-of-stay in each state. From

this graph, we deduce automatically the

corresponding Markov chain model. For the sake of

simplicity, we only present in the article, the case

where k=1. It is evident that in this case, we can use

a bi-gram. But we have also study the evolution with

k=2..n.

In perspective, we have to extend and to validate

our approach on different models such that Hidden

Markov Models which are widely used in many

patterns recognition areas. We have to study in more

details probabilistic automata and discrete hidden

models in order to clarify the links between them

(Dupont et al., 2005).

It could be interesting to study other classes of

diseases. Approximately 1-1,5 % French population

suffer from dementia and the causes of dementia are

neurological disorders such as Alzheimer's disease

(causes 50 percent to 70 percent of all dementia),

blood flow-related (vascular) disorders such as

multi-infarct disease, inherited disorders such as

Huntington's disease, and infections such as HIV

(Khachaturian, 2007). In fact, we would like to

simulate the patient’s progress in order to forecast

and to analyze the facility needs for long, medium

and short-term care in order to dimension the

human, financial and physical resources necessary in

the future.

ACKNOWLEDGEMENTS

The authors would like to acknowledge

Mr. F. Navarro (Chairman of the Board of

“Mutualité Française” Rhône-Alpes - France), as

well as all the staff who had the kind enough to

entrust us this project, data to validate our models

and who answered our numerous questions.

The authors are very grateful to the reviewers for

their comments which were both useful and helpful.

REFERENCES

Alur, R., Courcoubetis, C., Dill, D., 1990. Model-checking

for real-time systems. In Proceedings of the Fifth

IEEE Symposium on Logic in Computer Science, 414-

425.

Alur, R., Courcoubetis, C., Dill, D., 1991. Model-checking

for probabilistic real-time systems. In Automata,

Languages and programming: Proceedings of the 18th

ICALP, Lecture Note in Computer Science 510.

Alur, R., Dill, D., 1994. A theory of timed automata.

Theoritical Computer Science, 126, 183-235.

Angluin, D., Smith, C. H., 1983. Inductive inference:

Theory and methods, ACM Computing Surveys 15 (3),

237–269.

Angluin, D., 1987. Learning regular sets from queries and

counterexamples. Information and Computation, 75,

87–106.

Balczar, J. L., Daz, J., Gavald R., 1997. Algorithms for

learning finite automata from queries: A unified view.

In Advances in Algorithms, Languages, and

Complexity, 53–72.

Bugalho, M., Oliveira, A., 2005. Inference of regular

languages using state merging algorithms with search.

Pattern Recognition, 38(9), 1457–1467.

Combes, C., Azéma, J., Dussauchoy, A., 2008. Coupling

Markov model – optimization: an application in

medico-social care, 7e International Conference

MOSIM’08 - march 31th - April 2th, Paris – France,

1310-1319.

Combes, C., Azéma, J., 2013. Clustering using principal

component analysis applied to autonomy-disability of

elderly people. Decision Support System,

http://dx.doi.org/10.1016/j.dss2012.10.016.

Dupont, P., Denis, F., Esposito Y. 2005. Links between

probabilistic automata and hidden Markov models:

probability distributions, learning models and

induction algorithms. Patterns Recognition, 38(9),

1349-1371.

Garcia, P., Vidal, E., 1990a. Inference of k-testable

languages in the strict sense and applications to

syntactic pattern recognition. IEEE Transactions on

ContributionofProbabilisticGrammarInferencewithk-TestableLanguageforKnowledgeModeling-Applicationon

AgingPeople

459

Pattern Analysis and Machine Intelligence, 12 (9),

920-925.

Garcia, P., Vidal, E., Oncina, J., 1990b. Learning Locally

Testable Language In Strict Sense. In Proceedings of

the Workshop on Algorithmic Learning Theory, by

Japanese Society for Artificial Intelligence.

(http://users.dsic.upv.es/grupos/tlcc/papers/fullpapers/

GVO90.pdf).

Grinchtein, O., Jonsson, B., Leucker, M., 2005. Inference

of Timed Transition Systems. In Proceedings of

International Workshop on Verification of Infinite

State Systems, Electronic Notes in

TheoreticalComputer Science, 138(3):87-99.

Khachaturian, Z. S., 2007. A chapter in the development

of Alzheimer’s disease research: a case study of public

policies on the development and funding of research

programs. Alzheimer’s & dementia: the journal of the

Alzheimer’s Association 3(3), 243–258.

Parekh, R., Honavar, V., 2001. Learning DFA from simple

examples. Machine Learning, 44(1/2), 9–35.

Parekh, R., Nichitiu C. M., Honavar, V., 1998. A

polynominal time incremental algorithm for learning

DFA. In Proceeding of International Colloquium on

Grammatical Inference: Algorithms and Applications,

37–49.

Rico-Juan, J., Calera-Rubio, J., Carrasco, R., 2000,

Probabilistic k-testable tree languages, In A. Oliveira

(Ed.), Proceedings of 5th International Colloquium,

ICGI, Lisbon (Portugal), Lecture Notes in Computer

Science, vol. 1891, Springer, 221–228.

Rivest, R.L., Schapire. R.E., 1993. Inference of finite

automata using homing sequences. Information and

Computation, 103, 299–347.

Verwer, S., de Weerdt M., Witteveen, C., 2007. An

algorithm for learning real-time automata. In

proceedings of the 18

Benelearn, P. Adriaans, M. van

Someren, S. Katrenko (eds.).

Verwer, S., de Weerdt M., Witteveen, C., 2011. The

efficiency of identifying timed automata and the

power of clocks. Information and Computation, 209

(3), 606-625.

Vidal, E., Thollard, F., de la Higuera, C., Casacuberta, F.,

Carrasco, R.C., 2005. Probabilistic Finite-States

Machine, IEEE Transactions on Patterns Analysis and

Machine Intelligence, 27 (7), 1013-1039.

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

460