
Parameterization of Written Signatures based on EFD
Pere Marti-Puig, Jaume Danés and Jordi Solé-Casals
Group of Digital Technologies, University of Vic, C/ de Laura 13, 08500 Vic, Barcelona, Spain
Keywords: Quantitative Shape Analysis, Elliptical Fourier Descriptors (EFD), Handwriting Recognition, Biometrics.
Abstract: In this work we propose a method to quantify written signatures from digitalized images based on the use of
Elliptical Fourier Descriptors (EFD). As usually signatures are not represented as a closed contour, and
being that a necessary condition in order to apply EFD, we have developed a method that represents the
signatures by means of a set of closed contours. One of the advantages of this method is that it can
reconstruct the original shape from all the coefficients, or an approximated shape from a reduced set of them
finding the appropriate number of EFD coefficients required for preserving the important information in
each application. EFD provides accurate frequency information, thus the use of EFD opens many
possibilities. The method can be extended to represent other kind of shapes.
1 INTRODUCTION
The quantitative shape analysis that is sometimes
required in biometrics, agronomy, medicine,
genetics, ecology or taxonomy, among other
research fields, is commonly performed on the
contours extracted from images (Lestrel, 1997). One
of the major problems when performing an
automatically quantification of contour sets is the
large amount of data involved in describing the
shape. As a result, previous to the application of a
known analysis or classification technique, the
contours are parameterized. Then, with suitable
contour parameterization, the most relevant shape
information for a particular purpose can be
represented with a reduced number of coefficients.
Although different contour descriptors have been
developed, the most widely used are the Elliptical
Fourier Descriptors (EFD) that are applied to the
(x,y) contour coordinates. EFD were first proposed
by Kuhl and Giardina (Kuhl and Giardina, 1982) and
one of the reasons for its wide acceptance is because
EFD can represent all kinds of close curves as well
as preserve the original shape information when
shape reconstruction is required, using only a limited
number of coefficients, providing intuitive
information about the number of coefficients
required to preserve a given level of detail of the
shapes. EFD can also be prepared to be invariant to
translation, rotation and scale (Nixon and Aguado,
2008). There exist many fields that use EFDs for
shape quantization. We found some examples
applied to the characterization of biological contours
of animals (Rohlf and Archie, 1984); (Bierbaum and
Ferson, 1986); (Diaz et al., 1989); (Ferson et al.,
1985); (Castonguay et al., 1991); (Chen et al., 2000);
(Tort, 2003); (Tracey et al., 2006) and applied to the
contours of plants (Iwata et al., 2000); (Iwata and
Ukai, 2002); (Iwata et al., 2004). Concerning the
practical uses of EFD, although the reconstruction of
any discrete contour can be perfect with the
appropriate number of EFD coefficients, in realistic
applications a good balance between the
preservation of the relevant shape information and
interesting data dimensional reduction must be done.
Hence, only a part of the coefficients are selected.
2 ELLIPTICAL FOURIER
CONTOUR DESCRIPTORS
OVERVIEW
As it is well-known, a continuous close contour with
period T is defined by the evolution of its
coordinates x(t) and y(t) along the variation of t. The
contour coordinates can be expanded using the
Fourier series. The contour coordinates, in its
equivalent real or complex forms, can be written as:
439
Marti-Puig P., Danés J. and Solé-Casals J. (2013).
Parameterization of Written Signatures based on EFD.
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing, pages 439-444
DOI: 10.5220/0004359004390444
Copyright
c
SciTePress

k
k
t
T
k
j
k
k
kk
eu
T
kt
b
T
kt
aatx
2
1
0
2
sin
2
cos)(
(1)
k
k
t
T
k
j
k
k
kk
ev
T
kt
d
T
kt
ccty
2
1
0
2
sin
2
cos)(
(2)
where:
dtetx
T
u
t
T
k
j
T
k
2
.
)(
1
(3)
dtety
T
v
t
T
k
j
T
k
2
.
)(
1
(4)
with:
*
kkk
uua
and
*
kkk
uujb
(5)
*
kkk
vvc and
*
kkk
vvjd
(6)
The real coefficients a
k
, b
k
, c
k
and d
k
become an
alternative to perfectly describe the contour and are
known as Elliptic Fourier coefficients. It is easy to
see from (3) and (4) that the coefficients a
0
and c
0
only represent the position of the centre of gravity of
the shape contour. If a
0
and c
0
take the zero value the
contour is centred in the origin. The contour
approximation based on the EFD is achieved by
selecting a reduced set of coefficients, i.e. by
limiting the number of harmonics in the following
way:
K
k
nkK
T
kt
b
T
kt
aatx
1
0
2
sin
2
cos)(
(7)
K
k
kkK
T
kt
d
T
kt
ccty
1
0
2
sin
2
cos)(
(8)
Clearly the approximations x
K
(t) and y
K
(t) improve
as K increases.
3 EFC DESCRIPTORS AND ITS
RELATION TO THE DFT
The contours from 2D images have a discrete nature
and what we really have are the discrete signals x(n)
and y(n) which can be thought of as sampled
versions of x(t) and y(t) at the instants t=nT/N where
n goes from 0 to N-1. In practice, then, we have the
N pair of points (x(n),y(n)) of a fundamental period.
In order to show how the Fourier series expansion of
the discrete signals x(n) and y(n) can be related to
the DFT let us first consider the expansion of x(t) in
(1) and its complex equivalent expression in the
following way:
k
k
t
T
k
j
k
t
T
k
j
ko
k
k
t
T
k
j
k
k
kk
eueuueu
T
kt
b
T
kt
aatx
1
222
1
0
2
sin
2
cos)(
(9)
With the aim of obtaining the discrete signal x(n)
and y(n) from the continuous ones, the following
changes must be applied. First t has to be replaced
by the discrete values nT/N (n=0,...,N-1) in (9).
Second, taking into account that the discrete lowest
frequency able to represent is
1
=2π/N and the
highest is
k
=π the set of analogical frequencies
k
=2πk/T from k going from 0 to becomes
k
=2πk/N where index k goes from 0 to N/2. Then x(n)
takes the form:
2/
1
22
2/
2/
2
2/
1
0
2
sin
2
cos)(
Nk
k
kn
N
j
k
kn
N
j
ko
Nk
Nk
kn
N
j
k
N
k
kk
eueuueu
kn
N
bkn
N
aanx
(10)
In the same way, the coefficients u
k
can be found
from (3) by replacing the integral by a summation,
the continuous variable t by its samples nT/N and dt
by the minimum increment T/N:
1
0
2
1
0
2
)(
1
)(
1
N
n
kn
N
j
N
n
N
Tn
k
T
j
k
enx
NN
T
enx
T
u
(11)
Then, from the DFT definition, the coefficients u
k
can be obtained as:
)(
1
kX
N
u
k
(12)
Where X(k) is the k-th element of the DFT of x(n).
Let us remember the well-known conjugate
symmetry DFT property (Proakis and Manolakis
1996):
)()()(
*
kNXkXkX
(13)
This means that u
-k
= u
k
*
(where symbol * denotes
the conjugation operation), then using (13) the last
term of (11) becomes:
2/
1
2
*
2
)(
Nk
k
kn
N
j
k
kn
N
j
ko
eueuunx
(14)
By writing u
k
in the polar form u
k
=|u
k
|e
jk
, using the
BIOSIGNALS2013-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
440

Euler formula and applying the well known equality
cos(A+B)=cos(A)cos(B)-sin(A)sin(B), we have:
kn
N
ukn
N
uu
kn
N
uu
eeuunx
kk
Nk
k
kko
Nk
k
kko
Nk
k
jkn
N
jjkn
N
j
ko
kk
2
sinsin2
2
coscos2
2
cos2
)(
2/
1
2/
1
2/
1
22
(15)
As a result, from (11) and (15) it is easy to obtain the
EFD coefficients of x(n) from the DFT of x(n).
Similarly, as y(n) has an expression formally
identical to x(n) the coefficients c
k
and d
k
are also
obtained from the DFT of y(n). Therefore we have:
N
X
ua
)0(
00
(16)
N
Y
vc
)0(
00
(17)
N
kX
ua
kkk
)](Re[2
cos2
(18)
N
kX
ub
kkk
)](Im[2
sin2
(19)
N
kY
vc
kkk
)](Re[2
cos2
(20)
N
kY
vd
kkk
)](Im[2
sin2
(21)
where X(k) and Y(k) are the DFTs of x(n) and y(n)
respectively. The discrete signal approximation of
x
K
(n) and y
K
(n) (K < N/2) takes the form as:
K
k
kkK
kn
N
bkn
N
aanx
1
0
2
sin
2
cos)(
(22)
K
k
kkK
kn
N
dkn
N
ccny
1
0
2
sin
2
cos)(
(23)
Note that the DFT can be efficiently computed by its
fast algorithm, the FFT, which can also be optimised
for real data (Proakis and Manolakis, 1996). Note
also that the elliptic Fourier descriptors can be
modified to be invariant with respect to size,
rotation, or starting point (Nixon and Aguado,
2008).
On the left of figure 1, a 2D butterfly contour is
represented and on the right the sequences of 1024
points of x(n) and y(n) are depicted. In figure 2,
following the same distribution, we can see the
contour reconstruction, on the left, and the x(n) and
y(n) reconstructions taken only the first 72
coefficients, 36 for x(n) and 36 y(n), on the right.
Figure 1: On the left, image contour. On the righ,
representation of the contour coordinates y(n) and x(n).
Figure 2: On the left, image contour reconstruction using
EFD given 72 real coefficients. On the right,
representation of the contour coordinates reconstruction
employing the first 36 real coefficients for both x(n) and
y(n).
In some applications it is interesting to obtain the
coefficients representing a contour independently of
position, scale factors or rotations. From (16) and
(17), according to Nixon and Aguado (Nixon and
Aguado, 2008), it is easy to see than the coefficients
a
0
and b
0
represent the centre of the contour. By
imposing a
0
=b
0
=0 the contour reconstruction is
centred at the origin of coordinates. So, this is the
condition to modify the parameters to be
independent of the position. To be scale invariants,
normalization of the set of parameters by S is
required, being S = max{a
1
,b
1,
c
1
,d
1
} (Nixon and
Aguado 2008). The invariance to rotation requires
defining a new set of parameters in the following
way (Nixon and Aguado 2008):
2
2
22
22
k
k
kk
kk
K
v
u
dc
ba
r
(24)
4 PROPOSED
PARAMETERIZATION
METHOD
In order to compare and quantify written signatures
we will use images. A digital camera or a scanner
can be used to obtain the images of the signatures. If
the image is taken with a minimum quality by
simple image processing techniques we obtain the
ParameterizationofWrittenSignaturesbasedonEFD
441

different closed contours of the signature. Each
signature can contain a particular number of closed
contours with different number of points. The basic
idea of the proposed method is the following: a
signature is decomposed in different closed contours
that are ordered from the longest to the lower. Then
we consider only the M longer contours. Each of
these contours is parameterized by a reduced number
of N EFD coefficients that are ordered sequentially.
When the signature has only L closed contours,
L<M, the last (M-L)N parameters will be zero. In
figure 3 the level of the EFD coefficients with
respect to its index (k) is presented, showing that the
coefficients with lower index are more important
than the coefficients with higher index. If we
consider the characterization of the N most
important contours per signature, and a signature has
less than N contours we complete the difference
with zeros. Depending on the application, we can
consider the modification of the parameters in order
to achieve invariance to scale and rotation,
maintaining a relative position of the closed contours
with respect to the centre of masses of the signature.
We show the process by an example.
In figure 4 we show the reconstruction of a
signature using 40, 30, 20 and 10 complex
coefficients per contour.
Figure 3: Representation of the EFD coefficients with its
index.
The signature used in figure 5 has only 7
contours. On the following figures (6 and 7), for the
same example, we show the detail of 3 of these
contours with the axis indicating position
information.
5 DISCUSSION AND FUTURE
WORK
The proposed parameterization can be easily used
for characterizing signatures or words of different
people. As the original images are static images
(scanned of photo images), the kind of applications
that can profit of this technique are related to off-line
handwritten signature verification. One of the
challenging problems in this field is the feature
extraction process. Our system can be a good
strategy in order to improve verification results and
specially in order to develop a general system to
classify every signature. Therefore, we are now
putting our efforts in exploring the generalization
capability of our extracted parameters for signature
verification and writer recognition using EFD as
parameters and different kind of linear and nonlinear
classifier. It is important to note that writer
recognition using short words has been recently
studied in (Sesa-Nogueras and Faundez-Zanuy,
2012) and very good results have been obtained for
text-dependent writer recognition.
Figure 4: Representation of the original image, the contour
extracted from the original image and some
reconstructions using different number of EFD
coefficients.
BIOSIGNALS2013-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
442
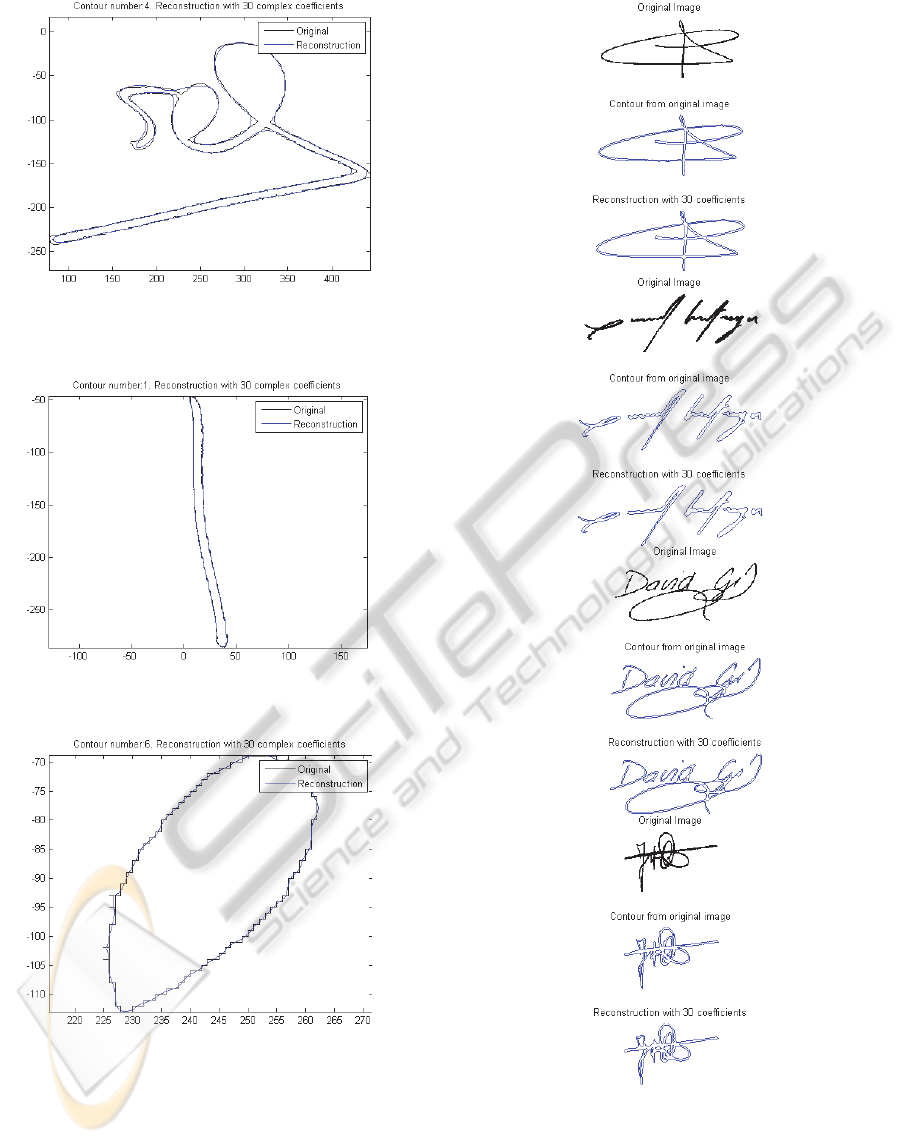
Figure 5: The longer contour with its reconstruction using
30 complex coefficients.
Figure 6: The second longer contour with its
reconstruction using 30 complex coefficients.
Figure 7: Another contour and its reconstruction.
Figures 8 provide some other kind of signatures
with its reconstructions.
6 CONCLUSIONS
In this work we show a way to apply the Elliptic
Figure 8: Another contour ad its reconstruction.
Fourier analysis to the parameterization of
signatures. We analyse also the relation of the
coefficients given by Kuhl and Giardiana with the
complex coefficients computed with the FFT in
order to obtain a fast method for the EFD derivation.
ParameterizationofWrittenSignaturesbasedonEFD
443

An important advantage when using the proposed
kind of parameters is that from a reduced set of
coefficients we can obtain an approximate
reconstruction of the original shape, controlling the
preserved or discarded information in order to
optimize the performance for each application. One
of the advantages of this method is that it allows
comparison of different signatures of the same
person taken in different times.
ACKNOWLEDGEMENTS
This work has been supported by the University of
Vic under the grant R0904.
REFERENCES
Bierbaum R. M., Ferson S., 1986. Do symbiotic pea crabs
decrease growth rate in mussels? Biol Bull. 170:51-61.
Castonguay, M., Simard, P., and Gagnon, P., (1991)
Usefulness of Fourier analysis of otolith shape for
Atlantic mackerel (Scomber scombrus) stock
discrimination. Can.J.Fish.Aquat.Sci. 48(2):296-302.
Chen, S. Y. Y., Lestrel, P. E., Kerr, W. J. S., McColl, J.
H., (2000) Describing shape changes in the human
mandible using elliptical Fourier functions. Eur. J.
Orthodont. 22, 205–216.
Diaz G., Zuccarelli A., Pelligra I., Ghiani A., 1989.
Elliptic Fourier analysis of cell and nuclear shapes.
Comp Biomed Res. 22:405-414.
Ferson S., Rohlf F. J., Koehn R. K., 1985. Measuring
shape variation of two-dimensional outlines. Syst Zool.
34:59-68.
Iwata H, Niikura S, Matsuura S, Takano Y, Ukai Y,
(2000). Diallel analysis of root shape of Japanese
radish (Raphanus sativus L.) based on elliptic Fourier
descriptors. Breed Sci. 50:73-80.
Iwata, H., Ukai, Y., (2002): SHAPE: a computer program
package for quantitative evaluation of biological
shapes based on elliptic Fourier descriptors. J. Hered.
93, 384–385.
Iwata, H., S. Niikura, S. Matsuura, Y. takano and Y. Ukai
(2004) Interaction between genetic effects and soil
type in diallel analysis of root shape and size of
Japanese radish (Raphanus sativus L.). Breeding
Science 54: 313-318.
Kuhl, F. P., Giardina, C. R., (1982). Elliptic Fourier
features of a closed contour. Comput. Graph. Image
Process. 18, 236–258.
Lestrel, P. E. (Ed.)., (1997): Fourier Descriptors and their
Application in Biology. Cambridge University Press,
UK, p. 466.
Nixon, M., Aguado A. (2008): Feature Extraction and
Image Processing (2 Ed.) Academic Press.
Rohlf F. J., Archie J. W., (1984). A comparison of Fourier
methods for the description of wing shape in
mosquitoes (Ritera culicidae). Syst Zool. 33:302-317.
Sesa-Nogueras, E., Faundez-Zanuy, M., (2012) Biometric
recognition using online uppercase handwritten text.
Pattern Recognition 45, 128-144.
Tracey, S. R., Lyle, J. M., Duhamelb, G., (2006)
Application of elliptical Fourier analysis of otolith
form as a tool for stock identification. Fisheries
Research 77, 138–147
Tort, A., (2003) Elliptical Fourier Functions as a
Morphological Descriptor of the Genus Stenosarina
(Brachiopoda, Terebratulida, New Caledonia). Math.
Geology, 35 (7), 873-885.
BIOSIGNALS2013-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
444
