Model-based Control Approaches for Optimal Integration of a Hybrid

Wind-diesel Power System in a Microgrid

Luis Ismael Minchala Avila

1,2

, Adriana Vargas Mart

ınez

, Youmin Zhang

Luis Eduardo Garza Casta

, Eduardo Robinson Calle Ortiz

and Julio C

esar Viola

Department of Mechatronics and Automation, Tec. de Monterrey, Eugenio Garza Sada 2501, Monterrey NL, Mexico

Department of Mechanical and Industrial Engineering, Concordia University, 1455 de Maisonneuve, Montreal, Canada

Engineering Research Center for Innovation and Development, Universidad Polit

ecnica Salesiana,

Calle Vieja 12-30, Cuenca, Ecuador

Keywords:

Distributed Generation, Hybrid Wind-diesel, Microgrids, Model Predictive Control, Model Reference

Adaptive Control.

Abstract:

This paper presents two model-based approaches for designing control strategies in order to integrate a diesel

generator as frequency and voltage leader in an islanded microgrid conﬁguration. The selected microgrid

conﬁguration is composed of a hybrid wind-diesel system with a battery storage system (BSS). A model

predictive control (MPC) scheme and a model reference adaptive control (MRAC) scheme are selected for

this task, due to its ﬂexibility and capability for handling constraints and fault-tolerance, respectively, which is

helpful for smart grid (SG) architectures to achieve reduced fuel consumption and with and enhanced reliability

and integration of renewable energy sources (RES) into the electrical network. A constrained fuel consumption

strategy has been implemented in the diesel engine generator (DEG) controller with the help of MPC strategy

and fault-tolerance is achieved with MRAC. Different operating conditions of the microgrid were simulated: 1)

diesel-only generation, 2) wind turbine generator (WTG) ignition, 3) sudden connection of 0.5 MW load, and

4) a 3-phase fault with duration of 0.5 seconds. Improved performance over a baseline controller, IEEE type 1

automatic voltage regulator (AVR), is achieved. Dynamic models of the network components are presented in

details on design and implementation of the microgrid conﬁguration in Matlab/Simulink



1 INTRODUCTION

Microgrids are small-scale low voltage power sys-

tems with distributed energy resources (DER), sto-

rage devices and controllable loads, connected to the

main power network or islanded. Microgrids are

concerned with power generation near the consumers

(Jiang et al., 2009; Gentile, 2009). Nevertheless, mi-

crogrids have different operating characteristics than

bulk power systems (BPS) such as lack of inertia, re-

sistive lines and high penetration of RES.

Microgeneration units, typically located at users

locations, have emerged as an option to meet grow-

ing customer needs for electric power with an em-

phasis on reliability, power quality, and contribution

to different economic, environmental and technical

beneﬁts. The impact on power balance and grid fre-

quency of microgeneration at low voltage levels, such

as wind energy or photovoltaic (PV), is a great cha-

llenge (Schwaegerl et al., 2009). Wind is a promis-

ing RES due to its cleanness and social impact moti-

vated by environmental and economical issues. How-

ever, wind energy also has some limiting characteris-

tics such as: unschedulable, uncontrollable, etc. To

obtain relatively constant power, variable blade pitch

angle controls are installed in the wind turbines (WT)

(Abdin and Xu, 2000; Abdal et al., 2010).

There is a variety of contributions on the ﬁeld

of simulating and controlling a hybrid wind-diesel

power system. In (Vechiu et al., 2004; Kini and Yara-

gatti, 2006) detailed models of the system compo-

nents of the hybrid conﬁguration are presented, as

well as performance analysis under different operat-

ing conditions, i.e. different wind velocities, load

changes, etc., where IEEE type 1 AVR has been

used. A fully distributed control strategy for a mi-

crogrid conﬁguration integrating a WTG through DC-

link voltage control is studied in (Vandoorn et al.,

Minchala Avila L., Vargas Martínez A., Zhang Y., Eduardo Garza Castañón L., Robinson Calle Ortiz E. and César Viola J..

Model-based Control Approaches for Optimal Integration of a Hybrid Wind-diesel Power System in a Microgrid.

DOI: 10.5220/0004359400120021

In Proceedings of the 2nd International Conference on Smart Grids and Green IT Systems (SMARTGREENS-2013), pages 12-21

ISBN: 978-989-8565-55-6

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

2011), where two loops control strategy (voltage and

power) is designed and simulated for the WTG. In

(Kassem and Ali, 2011) a robust control approach for

long term operation of a hybrid wind-diesel system

is presented, a linearized model of the entire system

is proposed through the combination of the subsys-

tem models, and it is used for the design of a central-

ized controller. A MPC strategy has been used for a

stand-alone wind energy conversion system (WECS)

in (Kassem, 2012) and a novel functional MPC is pro-

posed for a faster processing time.

Frequency and voltage regulation in interco-

nnected electrical systems with multiple sources ge-

neration are main control challenges in distributed

generation systems. Many different approaches have

been studied and proposed for both grid-connected

and islanded microgrid operation. Grid-connected

operation relies on main grid parameters and the ma-

jority of contributions are related with volt-var strate-

gies through the use of capacitor banks and ﬂexible

AC transmission system (FACTS), although advanced

control strategies like adaptive controllers for volt-

age regulation at the generation unit are detailed in

(Fusco and Russo, 2008; Fusco and Russo, 2012).

Islanded microgrid operation, on the other hand has

generated the necessity of a frequency leader, or mul-

tiple frequency leaders under faulty scenarios, due to

the high integration of RES whose intermittent cha-

racteristic complicates the use of traditional control

schemes. Voltage and frequency regulation for iso-

lated generators are studied in some research papers;

in (Munoz-Aguilar et al., 2011) a sliding mode con-

trol for voltage amplitude regulation of a stand-alone

synchronous generator connected to a resistive load is

presented, while in (Kumar et al., 2008) a frequency

regulator for a microgrid conformed by a diesel gen-

erator, a wind turbine power, an aqua electrolyzer

and a fuel cell through multiple PI controllers is pro-

posed. A multiagent-based automatic generation con-

trol (AGC) for isolated power systems with dispersed

power sources such as PV, WTG, diesel generator and

energy capacitor systems (ECS) for the energy stor-

age is very well detailed in (Hiyama, 2011).

This paper presents the design methodology for

controlling a hybrid wind-diesel system in islanded

microgrid conﬁguration using two model-based con-

trol approaches: MPC and MRAC. MPC is used for

optimizing RES utilization and minimizing fuel con-

sumption of the DEG with the help of MPC’s opti-

mized performance with constraints handling capabil-

ities. MRAC is used for controlling the system un-

der faulty scenarios due to its capability of adapting

the control output for guaranteeing asymptotic out-

put tracking. The control design objectives are to

maintain desired voltage and frequency (frequency &

voltage leader), and supply energy for the balanced

load (total load - WTG power). With the model de-

veloped for each network component, a distributed

control strategy is then proposed. Different operating

conditions of the microgrid were simulated: 1) diesel-

only generation, 2) wind turbine generator (WTG) ig-

nition, 3) sudden connection of 0.5 MW load, and 4) a

3-phase fault with duration of 0.5 seconds. Improved

performance over a baseline controller, IEEE type 1

AVR, is achieved.

The paper is organized as follows: Section II

presents model generation of the microgrid compo-

nents. Section III deals with the controllers design.

Section IV presents simulation results and perfor-

mance analysis and ﬁnally conclusions are drawn in

Section V.

2 MODELING OF MICROGRID

A typical microgrid conﬁguration, consists of DG

units, controllable loads and storage. Fig. 1 presents a

typical microgrid architecture, where it is remarkable

the high penetration of RES and DC-links for inte-

grating these intermitent units into the main grid. In

the following subsections, detailed models of the net-

work componentes are presented.

Figure 1: A typical microgrid architecture.

2.1 Diesel Engine Generator

The DEG is composed of two machines: diesel en-

gine (prime mover) and synchronous generator. In

the following two subsections the diesel engine and

synchronous generator models are presented.

2.1.1 Diesel Engine

For a complete dynamic simulation of the diesel en-

gine, a high order model would be required. How-

ever, for speed control purpose (frequency control of

Model-basedControlApproachesforOptimalIntegrationofaHybridWind-dieselPowerSysteminaMicrogrid

the grid), a simpler model will be enough. Fig. 2

shows a block diagram of the diesel engine. The ac-

tuator block is modeled by a ﬁrst-order system with

a gain K

and a time constant T

. On the other hand,

the diesel engine block contains the combustion sys-

tem and it is responsible of the movement of the pis-

tons and in consequence the crankshaft will gener-

ate a torque T (s) in the shaft. Some research papers

(Kuang et al., 2000; Lee et al., 2008) use a time delay

−τs

and a torque constant K

for modeling this block.

The ﬂywheel block is an approximation of the com-

plex inertia dynamics generated inside the machine,

while the ρ coefﬁcient represents friction. The output,

(t) represents the angular velocity of the machine’s

shaft. d(s) is used for modeling load changes in ro-

tor shaft, e.g. larger mechanical power demanded for

the synchronous generator due to a connection of an

electrical load.

Figure 2: Classic diesel engine block diagram (Lee et al.,

2008).

The continuous-time model of Fig. 2 is repre-

sented in state-space equations, as follows:

˙x

(t) = −

(t) +

u(t) (1)

˙x

(t) = γK

(t − τ) −ργx

(t) (2)

x(t) = A

x(t) + A

x(t − τ) + B

u(t) (3)



−

0 −ργ



(4)



0 0

γK



(5)





(6)

System model (3) is a continuous time-delay state

space representation that needs to be discretized for

control design purposes. Many approaches for input-

delay discretization has been proposed (Zeng and Hu,

2010), while a simpler solution is presented in (Jugo,

2002), which is adopted in this study. Characteristic

values of the diesel engine constants in (3) are taken

from (Kuang et al., 2000) and summarized in Table 1.

Using a sampling time of 50 ms, one obtains:

x[k + 1] = x[k] +

∑

i=1



+ A



−1



x[k]



t + A

tµ



−1



dt u[k]

= 20;

x[k + 1] =



0.6703 0

0.0142 0.9985



x[k] +



0.3297

0.0030



u[k]

(7)

(8)

Table 1: Typical parameters of a diesel engine.

System parameter Value range Nominal

Actuator gain K

(pu) 1.0 1.0

Actuator time T

(s) 0.05 − 0.2 0.125

Engine torque K

(pu) 0.8 − 1.5 1.15

Engine dead time τ (s) 0 − 1 0.5

Plant. ﬂywheel accel γ



−1



0.1 − 0.5 0.3

Friction coefﬁcient ρ (pu) 0.1 0.1

2.1.2 Synchronous Generator

The machine’s shaft is driven by a prime mover, i.e.,

steam, hydraulic turbine or diesel engine. The mag-

netic ﬁeld produced by the ﬁeld winding links the

stator coils to induce voltage in the armature wind-

ings as the shaft is moved by the prime mover. A

state-space model using the dynamic equations with

dq (direct-quadrature) as frame reference, through a

Park’s transformation, for a pure resistive load R

resistive load is used in the model, due to the fact

that a microgrid is mainly resistive) connected into the

synchronous machine is presented in (Munoz-Aguilar

et al., 2011) and is summarized as following:

= Ax + Bv

(9)

x =









A =





−(R

+ R

) ωL

−ωL

−(R

+ R

) −ωM

0 0 −R





L =





0 M

0 L





B =









where





are the dq stator and ﬁeld

currents, respectively; R

and R

are the stator and

SMARTGREENS2013-2ndInternationalConferenceonSmartGridsandGreenITSystems

ﬁeld resistances; L

, L

, and L

are the stator, mag-

netizing, and ﬁeld inductances; ω is the electrical

speed; v

and v

are the dq stator voltages; and v

is the ﬁeld voltage which will be used as a control

input. The parameters of the synchronous generator

used for the simulation are: Rs = 0.0036, L

= 0.08,

= 0.057014, L

= 0.1288, R

= 0.5, ω = 377,

= 39.65.

2.2 Wind Turbine Generator

This subsection presents the model details of a WTG,

where a horizontal-axis WT has been chosen as prime

mover and an induction generator for energy conver-

sion. This combination of WT and asynchronous ma-

chine is the most commonly WTG found in commer-

cial versions for generating powers ranging from a

few kilowatts up to 3 MW. The operating condition

of the wind turbine is classiﬁed into three regimes:

startup regime, sub-rated power regime and rated

power regime. Dynamic simulation and the controller

design are investigated in this work at rated power

regime.

2.2.1 Wind Turbine Model

A WT model has been proposed in (Abdin and Xu,

2000; Abdal et al., 2010), where a PID algorithm for

blade pitch control is mainly used. The WT model

that will be used here is a lumped mass one, i.e. it

does not model the double mass phenomenon. The

turbine is pitch controlled through the blade pitch an-

gle, β. The power coefﬁcient, C

characterizes the

WT which is function of both tip speed ratio, λ =

ΩR

and β, where R is the wind turbine rotor radius, Ω is

the mechanical angular velocity of the WT rotor and

is the wind velocity.

(λ,β) =



116



λ + 0.08β

−

0.035

+ 1



− 0.4β − 5



× 0.5716e

−21



λ+0.08β

−

0.035



+ 0.0039λ (10)

The dynamic output is the mechanical torque (T

)

of the WT and is expressed as:

ρARC

2λ

(11)

where ρ is the air density and A represents the swept

area by the blades.

2.2.2 Induction Generator

The electrical equations of induction generator model

in the dq reference frame can be expressed as:

= r

(12)

= r

−

(13)

= r



ω − ω



(14)

= r



ω − ω



(15)

where ω

is the base electrical angular velocity used

to calculate the inductive reactances. The mechanical

part is expressed in per unit as:

− T

) (16)

= ψ

− ψ

(17)

2.3 Storage Subsystem

An electrical battery is one or more electrochemical

cells that convert stored chemical energy into electri-

cal energy. Lead-acid batteries are fully charged if

one can measure an open-circuit voltage of fully dis-

charged battery cell(s). The term discharged means

that all free charges within the battery are zero and the

only voltage source is the cell(s) voltage, V

(Fuchs

and Masoum, 2011).

A simple nonlinear Thevenin model has been

adopted for mathematical modeling purpose in (Chi-

asson and Vairamohan, 2005), whose aim is to design

a discrete time estimator for the state of charge (SOC)

of the battery. This model takes into account the dy-

namic response of the battery, which is inﬂuenced by

the capacitive effects of the battery plates and by the

charge-transfer resistance. Fig. 3 shows the equiva-

lent circuit.

Figure 3: Equivalent circuit of lead-acid battery.

In order to design control strategies for charge and

discharge process of the battery, it is required to deﬁne

state space equations, leading to the following equa-

tions for the discharge process (charge process is sim-

ilar, except for using R

instead of R

Model-basedControlApproachesforOptimalIntegrationofaHybridWind-dieselPowerSysteminaMicrogrid

= R

i(t) +

[i(t) + i

(t)]dt

(t) =

[i(t) + i

(t)]dt

= R

(t)

(t) +

(18)

(t)

= −

(t) −

(t) +

(19)

(t) = V

(t) − R

(t) (20)

A linear (approximate) relationship between open

circuit voltage and SOC is used in several research

papers (Chiasson and Vairamohan, 2005; Carter et al.,

2012), leading to a simple equation for estimating bat-

tery’s SOC:

S(t) =

(t) − b

(21)

where b is the battery terminal voltage when S(t) =

0% and a is obtained knowing the value of b and v

at SOC = 100%.

3 CONTROLLERS DESIGN

Figure 4 depicts the hybrid wind-diesel power sys-

tem architecture that has to be controlled, where DC

stands for distributed controller, CB stands for circuit

breaker and ILVDCB for intelligent low voltage dc

breaker (Minchala et al., 2012). The proposed control

strategy is composed of three distributed controllers,

each one with speciﬁc tasks:

1. DC1 implements two non-decoupled MPCs as a

ﬁrst approach and two MRACs as a second ap-

proach that are in charge of regulating both grid

frequency and voltage amplitude. A diesel en-

gine is used as a prime mover which drags a syn-

chronous machine generator at a constant speed.

In an islanded conﬁguration, the frequency is de-

termined by the mechanical speed ω

which is

provided by the diesel engine, while the volt-

age amplitude is set by the synchronous generator

ﬁeld voltage.

2. DC2 is regarded with power generation control of

the WTG. In this ﬁrst stage of investigation, an un-

constrained MPC for a limited range of the blade

pitch angle, β between 0 to 10 degrees, has been

designed.

3. DC3 controls a bi-directional dc−dc converter to

manage battery charge and discharge. A classic

PWM modulation control for the boost and buck

converters is used.

Figure 4: Hybrid wind-diesel power system architecture.

3.1 MPC Design

An integrator for reducing the steady-state error in

closed-loop has been added to MPC designs. The

augmented state-space model for diesel engine, SM

and WTG can be obtained as follows (Wang, 2009):

(k + 1) = A

(k) + B

u(k) (22)

y(k) = C

(k) (23)

∆x

(k + 1) = A

∆x

(k) + B

∆u(k) (24)

∆x

(k) = x

(k) − x

(k − 1) (25)

∆u(k) = u(k) − u(k − 1) (26)

x(k + 1) = Ax + B∆u(k) (27)

x(k) =



∆x

(k + 1)

y(k + 1)



(28)

A =





(29)

B =





(30)

y(k) =





x(k) (31)

where A

, B

, C

and x

represent the state matrix,

input matrix, output matrix and state vector of the

model, respectively. The augmented model in state

space that includes the integrator is represented by A,

B, x and ∆u. MPC uses this explicit model to predict

future trajectories of system states and outputs. This

prediction capability allows to solve optimal control

problems online, where prediction error and control

input action are minimized over a prediction horizon,

. The optimization yields to an optimal control se-

quence as input and only the ﬁrst element from the se-

quence is used as the control signal for controlling the

system, while the whole optimization procedure is re-

peated over and over again in each sampling step. The

ﬁnal aim of MPC is to provide zero output tracking

error with minimal control effort. Designing a MPC

with constraints is equivalent to solving a quadratic

programming problem in order to ﬁnd the parameter

vector ∆U, which minimizes a cost function J subject

to inequality constraints as follows:

SMARTGREENS2013-2ndInternationalConferenceonSmartGridsandGreenITSystems

J = [R

− Fx (k

)]

− 2∆U

− Fx (k

)]

+ ∆U



Φ + R



∆U (32)

γ ≥ M∆U (33)

u(k) = u(k − 1) + ∆u(k) (34)

F =



CA CA

··· CA



(35)

Φ =







CB 0 ··· 0

CAB CB ··· 0

B CAB ··· 0

−1

B CA

−2

B ··· CA

−N







(36)

where R = r

×N

and r

is used as a tuning param-

eter for the desired closed-loop performance. R

is a

vector with length N

that allows a comparison be-

tween reference signal and model output, for which

case we assume that the reference, r(k) is constant

in the prediction horizon. M ∈ R

(

+4N

)

×N

and

γ ∈ R

(

+4N

)

×1

are adequate matrices that represent

every constraint in matrix form. Hildreth’s quadratic

programming algorithm has been used for updating

control law, whose processing time in every sampling

interval varies from less than 1 ms up to 35 ms (tic toc

instruction in Matlab), for a computer with an i7 2.3

GHz processor and 4 GB of RAM memory.

The following design parameters have been

adopted in the controllers:

• SM rotor speed controller: One of the aims of the

optimal integration of the diesel generator in the

microgrid is to reduce fuel consumption, giving

priority to the power coming from RES, in our

case from WTG. To achieve this objective, a hard

constraint on the control signal is imposed, al-

though softening this constraint will allow a better

performance as it will be shown in the simulation

results. The maximum tolerable frequency devia-

tion is ±3 and a hard constraint for y is imposed

according to this and ﬁnally neither accelerations

nor deaccelerations greater than 50% are allowed

and a constraint for this requirement is also con-

sidered.

= 20

= 10

= 20

0 ≤ u ≤ 0.8

−0.5 ≤ ∆u ≤ 0.5

0.97 ≤ y ≤ 1.03

• SM Voltage Output Controller. Due to a resistive

load has been considered in (9), a greater predic-

tion horizon than the preceding controller is con-

sidered, in order to assure system stability when

capacitive and inductive loads are connected into

the system. The only hard constraint is on the con-

trol signal, since it is not admissible to have val-

ues smaller than zero and greater than 2 in order

to avoid saturation phenomenoms in the SM mag-

netic circuit.

= 50

= 5

0 ≤ u ≤ 2

• WTG Power Controller. An unconstrained con-

troller for a pitch angle range from 0 to 10 de-

grees is used. A stable behaviour is reached out

of this range with this controller, although a de-

graded performance on settling time is obtained,

due to the nonlinear relationship between β and

generated power.

= 20

= 10

= 0.7

3.2 MRAC Design

The MRAC implements a closed-loop controller that

involves the parameters that should be optimized, in

order to modify the system response to achieve the

desired ﬁnal value. The adaptation mechanism ad-

justs the controller parameters to match the process

output with the reference model output. The refer-

ence model is speciﬁed as the ideal model behavior

that the system is expected to follow. The design ap-

proach chosen for this work is the one using the Lya-

punov theory, presented in (Astrom and Wittenmark,

1995) and adapted here:

e = y

process

− y

re f erence

= G

× u − G

re f

× u

(37)

where e, y

process

, y

re f erence

, G

, u, G

re f

and u

repre-

sent the error, process output, reference output, pro-

cess model, process input, reference model and con-

troller signal, respectively. For a second order system,

the implemented MRAC scheme has two adaptation

parameters: adaptive feedfoward gain θ

and adap-

tive feedback gain θ

. These parameters will be up-

dated to follow the reference model. Then, the input

is rewritten in terms of the adaptive feedforward and

adaptive feedback gains as follows:

Model-basedControlApproachesforOptimalIntegrationofaHybridWind-dieselPowerSysteminaMicrogrid

u = θ

× u

− θ

× y

process

(38)

The Lyapunov stability theorem establishes the

following: If there exists a function V : R

→ R be-

ing positive deﬁnite and its derivative:

∂V

∂x

∂V

∂x

f (x) = −W (x) (39)

is negative semideﬁnite, then the solution x(t) = 0 to

= f (x) f (0) = 0 (40)

is stable. If

is negative deﬁnite the solution will be

asymptotically stable. V denotes the Lyapunov func-

tion for the system. If

< 0 and V (x) → ∞ when ||x|| → ∞ (41)

the solution is globally asymptotically stable.

To design an MRAC controller using Lyapunov

theory, the ﬁrst step is to derive a differential equa-

tion for the error that contains the adaptation param-

eters. Then, a Lyapunov function and an adaptation

mechanism need to be established to reduce the error

to zero. The Lyapunov derivative function

is usu-

ally negative semideﬁnite. Therefore, determining the

parameter convergence is necessary to establish per-

sistently excitation and uniform observability on the

system and the reference signal (Nagrath and Gopal,

2008). The proposed Lyapunov function is quadratic

in tracking error and controller parameter estimation

error because it is expected that the adaptation mech-

anism will drive both types of errors to zero. From the

equation error dynamics (42) the proposed Lyapunov

function can be chosen as (43):

= −

−

e +

(θ

− 1) u

−

(42)

V (e,θ

,θ

) =



(θ

− 1)

(θ

)



(43)

where b

, γ and a

> 0.

Equation (43) will be zero when the error is zero

and the controller parameters are equal to the de-

sired values. The above Lyapunov function is valid

if the derivative of this function is negative. Thus, the

derivative of (44) is:

V = a

(θ

− 1)

dθ

(44)

Substituting (42) in the above equation and rear-

ranging the similar terms, equation (45) is obtained:

V = −e

− a

− b

)



dθ

+ γu



)



dθ

− γy

process



(45)

If the adaptation parameters are updated as:

dθ

= −γu

e and

dθ

= γy

process

e (46)

then,

V = −e

− a

(47)

It can be seen that (47) is negative semideﬁnite

which implies V (t) ≤ V (0). This ensures that e, θ

and θ

are bounded. Since a

> 0, a

> 0 and u

is bounded then y

re f erence

is bounded and therefore

process

= e + y

re f erence

is bounded as well. From the

boundedness and convergence set theorem it can be

concluded that the error e will go to zero (Nagrath

and Gopal, 2008).

To overcome the limitations of the simple MRAC

structure (smaller fault accommodation threshold

than the MRAC in combination with other structures),

a classical PID controller expressed in the form

PID = K

+ K

s (48)

is introduced in the feedforward part of the simple

MRAC scheme. The PID parameters were obtained

by using a genetic algorithm pattern search to track

the desired system trajectory with the Matlab



Op-

timization Toolbox. The desired closed-loop behav-

ior of the system is established through the model

reference trajectory when there is no fault in the sys-

tem. The parameters that need to be established for

the desired optimization are shown in Table 2.

Table 2: Matlab



Optimization Toolbox parameters.

Parameters Value

Step initial value 0

Step ﬁnal value 1

Step time 0

Rise time 6s

% Rise 90

Settling time 9s

% Settling 5

% Overshoot 20

% Undershoot 2

SMARTGREENS2013-2ndInternationalConferenceonSmartGridsandGreenITSystems

Then, the genetic algorithm (GA) obtains the best

parameter optimization (see Table 3). The desired re-

sponse is introduced in terms of rise time, stabiliza-

tion time and overshoots.

Table 3: Optimized PID parameters using GA.

Parameter PID

3.8748

2.6471

1.9347

The MRAC has an adaptation learning rate γ =

0.99 for simulations to be presented in next section.

4 SIMULATION RESULTS

The system architecture shown in Fig. 4 was imple-

mented in Matlab/Simulink



. System parameters are

shown in Table 4. Three different controllers for the

diesel engine generator were tested, the ﬁrst one is

the baseline diesel engine speed and voltage control

that Matlab has in its library, i.e. governor and PI

controller for the rotor speed control and IEEE type

1 AVR for maintaining the voltage amplitude of the

microgrid. The second control approach tested is the

MPC described in sub-section 3.1 and the third one

is the MRAC described in sub-section 3.2. Variable

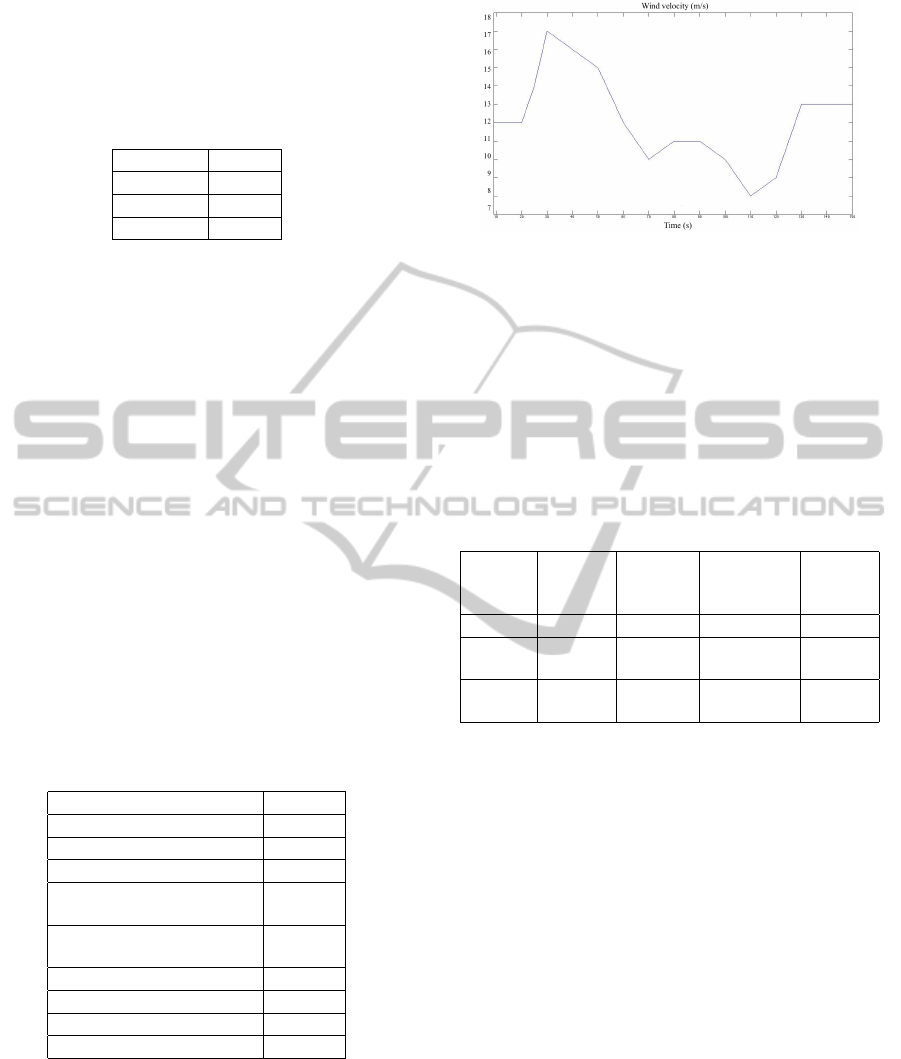
wind speed was used during the simulation, whose

velocity in every time instant of the simulation is de-

picted in Fig. 5.

Table 4: Hybrid wind-diesel system parameters.

Parameter Value

SM power 3 MVA

Grid voltage 220 V

Grid frequency 60 Hz

WT nominal mechanical

output

1.5 MW

WT max power at base

wind speed

0.85

Base wind speed 12 m/s

Load-1 2 MW

Load-2 0.5 MW

Load-3 0.4 MW

Fig. 6 shows the simulation results when the MPC

with softened constraint is used and Fig. 7 shows the

simulation results for the three control approaches.

The exact same events were tested in every case: (i)

when system is in steady state and WTG is off, then

suddenly WTG is turned on (after 12 seconds have

elapsed in the simulation) and the battery starts charg-

ing from 50% of SOC; (ii) when 50 seconds have

Figure 5: Wind velocity during the simulation.

elapsed, Load-2 is connected whose power consump-

tion is 0.5 MW; and (iii) a three-phase fault of 0.5 s of

duration is present in node-3 when 100 s of the simu-

lation time have elapsed. CB-32 disconnects every-

thing that is at its right side for isolating the fault.

MPC and MRAC show a much better performance

than the baseline controller and also they offer several

advantages over it, as summarized in Table 5.

Table 5: Advantages of MPC and MRAC over classic con-

trollers for DG integration in the microgrids.

Robust-

ness

Fault-

Tolerance

Constraints

Manage-

ment

Scalabi-

lity

MPC High Yes Yes High

MRAC Very

High

Yes No High

Classic

control

Low No No Low

A maximum power extraction from the WTG is

pretended by this network conﬁguration through pitch

angle control by a PID controller when the baseline

controller is used and unconstrained MPC when MPC

and MRAC are used in the diesel generator. Different

wind speeds are present, so 1 MW of power reference

is set in the WTG, and the balanced load (total load

- WTG power) is fed by the diesel engine. Battery

is charging from its initial SOC until full and is being

fed by an ac to dc converter with PWM control, whose

duty cycle has been set to 1.

5 CONCLUSIONS

A distributed MPC strategy and a MRAC with a PID

controller whose parameters were tuned using a GA

have been developed in this paper for an islanded mi-

crogrid conﬁguration which integrates the wind tur-

bine generator and diesel engine generator for more

efﬁcient electricity generation in the framework of

smart grids. Compared with a baseline controller, the

Model-basedControlApproachesforOptimalIntegrationofaHybridWind-dieselPowerSysteminaMicrogrid

Figure 6: System simulation with MPC controlling the diesel generator and the WTG.

Figure 7: Performance comparison for the three different control approaches.

developed controllers, MPC and MRAC, achieved a

better performance in both voltage and frequency re-

sponses. Softening the control signal constraint of the

diesel engine during WT ignition offered an improved

response in frequency control. Hard constraint on the

control signal of the diesel engine allows setting max-

imum fuel consumption and prioritizes energy gener-

ated by RES. A major advantage of MPC is its ability

to integrate constraints in the design that can be used

in a future work for FTC capabilities. On the other

hand the MRAC has an inherent capacity to accom-

modate perturbations and faults and direct physical

interpretation, and it is relative easy for implemen-

tation. Howerver, the use of only this type of con-

troller has certain limitations. For this reason, it is

normally to combine MRAC with other structures in

order to guarantee the system performance, to reduce

the unknown model dynamics, disturbances, to have

a better transient behavior, etc. It is important to re-

mark that the Lyapunov theory implemented to design

the MRAC guarantees closed-loop stability with also

fault-tolerant capabilities.

SMARTGREENS2013-2ndInternationalConferenceonSmartGridsandGreenITSystems

REFERENCES

Abdal, F., Abbas, R., and Abdulsada, M. A. (2010). Sim-

ulation of wind-turbine speed control by matlab. In-

ternational Journal of Computer and Electrical Engi-

neering, 2(5):912–915.

Abdin, E. and Xu, W. (2000). Control design and dynamic

performance analysis of a wind turbine-induction gen-

erator unit. IEEE Transactions on Energy Conversion,

15(1):91–96.

Astrom, K. and Wittenmark, B. (1995). Adaptive Control.

Addison-Wesley Publishing Company, 2nd edition.

Carter, R., Cruden, A., Hall, P., and Zaher, A. (2012).

An improved lead acid battery pack model for use in

power simulations of electric vehicles. IEEE Transac-

tions on Energy Conversion, 27(1):21–28.

Chiasson, J. and Vairamohan, B. (2005). Estimating the

state of charge of a battery. IEEE Transactions on

Control Systems Technology, 13(3):465–470.

Fuchs, E. F. and Masoum, M. A. (2011). Analyses and de-

signs related to renewable energy systems. In Power

Conversion of Renewable Energy Systems, pages 557–

687. Springer US.

Fusco, G. and Russo, M. (2008). Adaptive voltage regulator

design for synchronous generator. IEEE Transactions

on Energy Conversion, 23(3):946–956.

Fusco, G. and Russo, M. (2012). Nonlinear control design

for excitation controller and power system stabilizer.

Control Engineering Practice, 19(3):243–251.

Gentile, T. J. (2009). Smart grid a necessary component in

the remaking of america. IEEE-USA Annual Meeting.

Hiyama, T. (2011). Intelligent Automatic Generation Con-

trol. CRC-Press.

Jiang, Z., Li, F., Qiao, W., Sun, H., Wan, H., Wang, J., Xia,

Y., Xu, Z., and Zhang, P. (2009). A vision of smart

transmission grids. pages 1–10.

Jugo, J. (2002). Discretization of continuous time-delay

systems. In Proceedings of the 15th IFAC World

Congress, 2002, pages 117–122.

Kassem, A. M. (2012). Robust voltage control of a stand

alone wind energy conversion system based on func-

tional model predictive approach. International Jour-

nal of Electrical Power and Energy Systems, 41:124–

132.

Kassem, A. M. and Ali, M. Y. (2011). Robust control of an

isolated hybrid winddiesel power system using linear

quadratic gaussian approach. International Journal of

Electrical Power and Energy Systems, 33:1092–1100.

Kini, A. and Yaragatti, U. (2006). Modelling and simula-

tion of a wind/diesel hybrid power system. In Pro-

ceedings of the IEEE International Conference on In-

dustrial Technology, ICIT, pages 1670–1675.

Kuang, B., Wang, Y., and Tan, Y. L. (2000). An h

∞

con-

troller design for diesel engine systems. In Proceed-

ings of the International Conference on Power System

Technology, volume 1, pages 61–66.

Kumar, B., Mishra, S., Bhende, C., and Chauhan, M.

(2008). Pi controller based frequency regulator for

distributed generation. In Proceedings of the TEN-

CON - IEEE Region 10th Conference, pages 1 –6.

Lee, S.-H., Yim, J.-S., Lee, J.-H., and Sul, S.-K. (2008).

Design of speed control loop of a variable speed diesel

engine generator by electric governor. pages 1–5.

Minchala, L., Garza, L., and Calle, E. (2012). An intelli-

gent control approach for designing a low voltage dc

breaker. Number 4, pages 163–166.

Munoz-Aguilar, R., Doria-Cerezo, A., Fossas, E., and Car-

doner, R. (2011). Sliding mode control of a stand-

alone wound rotor synchronous generator. IEEE

Transactions on Industrial Electronics, 58(10):4888–

4897.

Nagrath, I. and Gopal, M. (2008). Control Systems En-

gineering. Anshan Ltd Press, United Kingdom., 5th

edition.

Schwaegerl, L., Tao, J.P.; Lopes, A., Madureira, P., Mancar-

ella, A., Anastasiadis, N., Hatziargyriou, and Krkol-

eva, A. (2009). Report on the technical, social, eco-

nomic, and environmental beneﬁts provided by micro-

grids on power system operation.

Vandoorn, T., Meersman, B., Degroote, L., Renders, B., and

Vandevelde, L. (2011). A control strategy for islanded

microgrids with dc-link voltage control. IEEE Trans-

actions on Power Delivery, 26(2):703–713.

Vechiu, I., Camblong, H., Tapia, G. B., and Dakyo, C. N.

(2004). Dynamic simulation model of a hybrid power

system: Performance analysis. 2004 European Wind

Energy Conference.

Wang, L. (2009). Model Predictive Control System Design

and Implementation Using MATLAB. Springer Pub-

lishing Company, Incorporated, 1st edition.

Zeng, L. and Hu, G.-D. (2010). Discretization of

continuous-time systems with input delays. Acta Au-

tomatica Sinica, 36(10):1426–1431.

Model-basedControlApproachesforOptimalIntegrationofaHybridWind-dieselPowerSysteminaMicrogrid