Joint MAS-PDE Modeling of Forest Pest Insect

Dynamics: Analysis of the Bark Beetle’s Behavior

David Picard, Aymeric Histace and Marie-Charlotte Desseroit

ETIS UMR 8051, ENSEA, University of Cergy-Pontoise, CNRS, Cergy-Pontoise, France

Abstract. This article deals with the social behavior modeling of a particular

forest pest insect: the bark beetle. This ant-like insect has been responsible for

the devastation of acres of pines trees in North America since 2005. Any tactic

of forest pest management requiring prediction of pest population change over

time and/or space, a realistic modeling of beetle colonies behavior would be a

real beneﬁt. The originality of this work is to propose a reactive Multi-Agent-

System integrating physical diffusion phenomena. The main idea is to take into

account the natural vanishing of the trail markers emitted both by decomposing

trees (ethanol) and the agents that have found a source of food (pheromone). The

proposed experiments show, on the one hand, that the MAS-PDE modeling leads

to a realistic global behavior of the colony when considering a usual foraging sce-

nario and, on the other hand, that, when compared with a simple reactive agent,

the proposed model has a faster convergence to the asymptotic usual expected

“S-shape” behavior of the agents’ colony.

1 Introduction

Modeling population dynamics is the essential part of both research and management

of forest pest insects. Any tactic of forest pest management requires prediction of pest

population change over time and/or space. However, the scope of prediction depends

on management objectives. An example of complex objective is to mi

nimize the impact of pest population on forest ecosystems during several years.

These kind of complex objectives require prediction of population changes over long

time intervals and over large areas. Of course, it is impossible to predict pest abundance

at speciﬁc location ten years ahead, but it may be possible to predict the change in

average pest population density as a result of some change in environment.

Formerly, to tackle this objective, mathematical modeling was the major tool for

predicting population dynamics and the reader could refer to Berryman and Millstein

[1] for a complete overview of some of the most known models that are mainly based

on modiﬁcations of discrete-time analog of the logistic model. The main advantage of

such methods is that parameters of these models can be adjusted to ﬁt available data.

Nowadays, mathematical modeling based approaches tend to be replaced by Multi-

gent Modeling (MAM) that has constituted an important research and development

area for the past two decades [2]. A MAM is formed of two elements, a Multi-agent Sys-

tem (MAS), and an environment in which the MAS evolves. When designing a Multi-

agent model (MAM), the modeler has control over the multi-agent system behavior and

Picard D., Histace A. and Desseroit M..

Joint MAS-PDE Modeling of Forest Pest Insect Dynamics: Analysis of the Bark Beetle’s Behavior.

DOI: 10.5220/0004362100290038

In Proceedings of GEODIFF 2013 (GEODIFF-2013), pages 29-38

ISBN: 978-989-8565-49-5

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

development and the environment. The latter is especially important in evolutionary

models as it determines the direction of the adaptation.

Fundamentally, a MAS is a system composed of multiple interacting agents within

an environment. The most simple MAS, called “reactive MAS” [3], assumes the behav-

ior of the agents can be modeled by a simple state machine (e.g. “resting”, “foraging”,

etc). These behavioral states often involve the modiﬁcation of the environment (for in-

stance the deposit of a pheromone) or interacting with other agents. Such agents do not

have have any memory capability, nor any decision making process. Thus, the switch

from one behavior to another is performed in reaction to some changes of the environ-

ment or due to some interactions with other agents. However, the collective behavior

of the MAS, emerging from the interactions of the agents with the environment, can

often be far more complex than that of the agents alone. Ant colonies are a good start-

ing example for such MAS: Although the local behavior of a single ant does not seem

to be controlled centrally, nor any explicit coordination between ants is observable, the

superorganism “ant colony” is able to construct complex nest architectures or adapt its

distribution of foragers to food sources in an efﬁcient way [4].

Cognitive MAS, based on a cognitive architecture, allows more complex behavior

modeling. A cognitive architecture can be deﬁned as the organizational structure of

functional processes and knowledge representations that enable the modeling of cogni-

tive phenomena like memory [5]. Nevertheless, such MAS needs to have a very deep

knowledge about the individual behavior of each single agent of the colony, which is

not always easy to model when too few parametric data are available from the expert

(entomologists for instance).

Considering now the “environment” of the Multiagent Model [6], the related dy-

namic is usually considered as a static phenomenon. It means that a food source will

only be modiﬁed (location, quantity) by the interacting agents of the MAS but not

by possible underlying external physical phenomena (like diffusion for example). This

could be considered as a limitation since the environment has a strong inﬂuence onto

the global behavior of the agents.

The aim of this article is to propose a MAM based on a simple reactive MAS and

the taking into account of evolution physical laws related to the corresponding environ-

ment. More precisely, we want to show that by integrating the way the resources and

the trail markers could naturally vanish (steered by a diffusive phenomenon parametri-

cally described using the spatio-temporal heat equation), we can obtain a more realistic

modeling of the global behavior of the MAS dynamics.

Practically speaking, we focus our attention on the behavior modeling of an so-

cial pest insect: the “Bark beetle”. Bark beetles are ecologically and economically sig-

niﬁcant [7] since outbreak species help to renew the forest by killing older trees and

other species aid in the decomposition of dead wood. However, several outbreak-prone

species are known as notorious pests that can cause tremendous damage to pine tree

forests for instance [8]. As a consequence, a better understanding of the social behavior

of this beetle would deﬁnitely be of some precious help to limit its damage capability.

This article is organized as follows: We ﬁrst introduce the bark beetle species with a

focus on the entomological data. Second, we introduce the proposed MAM that permits

to model the social behavior of the bark beetle with a taking into account of the physical

law steering the inner evolution of the available resources in a given environment. We

then propose an experimental section in which the behavior of the model is shown.

Finally, the obtained modeling results are discussed and concluded.

2 A Social Pest Insect: The Bark Beetles

2.1 Bark Beetles Description

Bark beetles are so-named because the best known species reproduce in the inner bark

(living and dead phloem tissues) of trees. Some species, such as the mountain pine bee-

tle (Dendroctonus ponderosae), attack and kill live trees. Most, however,live in dead,

weakened, or dying hosts. Once beetles ﬁnd a suitable host tree, they release aggregat-

ing pheromones to attract other beetles enabling a “mass attack” that can overwhelm

even a healthy tree defenses [7]. Along with releasing pheromones, the attacking bee-

tles introduce a staining fungus that infects and blocks the sapwood further weakening

the tree. Aggregating pheromones plus a pathogenic fungus infection help make rela-

tively healthy trees a quick meal for bark beetles.

Most bark beetles look the same to the casual observer. Bark beetles are usually less

than 5mm long, shiny brown to black, cylindrical, with hard wing covers.Basically, they

look like everyday beetles, only smaller (see Fig. 1(a) for illustration). Beetles spend

almost their entire life beneath tree bark. After mating, an “egg gallery” is excavated by

the female beetle, sometimes with help from a male friend. Eggs, laid along the sides

of the gallery, hatch within a few weeks. The larvae feed on the nutritious inner bark of

the tree, pupate, and then emerge as an adult. The adult beetle only spends a few days

outside the bark ﬂying to relocate to a new host.

(a) A typical bark beetle (b) Colony galleries on a dead tree

Fig.1.

Bark beetles excavate egg galleries like tiny tunnels in the live inner bark (Fig. 1(b)).

Engraver beetles score the sapwood, too. Larvae excavate “larval mines”. Bark beetle

galleries weaken the host tree and eventually kill it by girdling. Water and nutrient

transport in the live inner bark and in the outer edge of the sapwood are effectively

disrupted.

2.2 Ecological Role

Bark beetles and forests evolved together. In balanced forests, beetles have many bene-

ﬁcial roles. The most important are:

– Beetles “thin” naturally overstocked forests. Beetle-induced thinning is often irreg-

ular and patchy contributing to forest diversity. Gaps encourage changes in vegeta-

tion and forest structure beneﬁcial to wildlife.

– Beetles help recycle old forests. Beetles introduce wood decay fungi through the

bark where adults burrow into trees. Decay fungi help to rapidly decompose wood

and hasten nutrient recycling back into the soil.

– Beetle killed trees are a food source important to birds and other insect predators.

Snags provide roosting and nesting habitat.

However, due to peculiar warm climatic conditions, some deregulation could ap-

pear in the natural balance between forests and bark beetle population growing. As

a consequence, massive outbreaks of a speciﬁc species of bark beetles (the mountain

pine beetles) in western North America in 2005 have killed millions of acres of for-

est from New Mexico to British Columbia threatening increases in mudslides, forest

ﬁres and other adverse effects. A similarly aggressive species in Europe is the spruce

ips typographus. Another tiny bark beetle, the coffee berry borer, Hypothenemus

hampei is a major pest on coffee plantations around the world.

3 Modeling of Bark Beetles Behavior

In this section we explain the notations used in the paper, along with the physical quan-

tities we model.

3.1 Hypotheses and Notations

Bark beetles are social insects and consequently, the global behavior of a nest can be

modeled by a simple reactive MAS based on simple interaction among the different

agents. Three main hypothesis will steer the behavior of each agent : (i) They look for

food sources (pine trees for example) ; (ii) Once a food source is detected the agent

emit a particular pheromone that will strengthen the related path (the “trail markers”),

and (iii) food sources emit on their surroundings an attractor element (trees in decom-

position emit ethanol that naturally attract xylophagus insects).

For the experiments, we consider a 2D area of evolution. Each site of this area are

located using their cartesian coordinates (x, y). The following related notations are used

to characterize resources and agents:

Resources

Let s(x, y) denotes a food source (trees):

– the corresponding evolution law of the available resources is noted R

(t),

– the corresponding evolution law of the ethanol emission is noted E

(t),

– and E(x, y, t) denotes the quantity of ethanol at the coordinates (x, y) and for a

given instant t.

Agents

Let a(x, y) denotes an agent at the location (x, y) of the area

– n

(t) denotes the number of agents on a given site s,

– q

(t), the probability for a given agent a to quit the colony, at instant t,

– and p

(x, y, t) the probability of an agent to move to location (x, y), at instant t.

Moreover, agents are mobile only if they are not on a resources site.

4 Experiments

For all the following experiments, we will consider a closed homogenous SMA. Only

beetles will interact (no other types of agents) and that the total amount of agents will

stay the same (50 agents) all along the different experiments (no phenomenon like

“birth” or “death” of agents will be taken into account).

For all experiments, we use the usual logistic law to model the evolution of the

resources on a site:

(t + 1) = R

(t) − αn

(t) (1)

with α a given value representing the mean consumption rate of an agent between

two iterations of the evolving process. This non-linear choice is motivated by the fact

that numbers of agents related to a resource is not a ﬁxed value all along the process.

4.1 Agents Departure Modeling

In this ﬁrst scenario, only one resource is considered and 50 agents are located on it. We

want to test the effect of resources exhaustion on the mobility of the agents. We propose

to model the probability of departure of an agent by the ration of available resources at

time t:

(t) = 1 −

(t)

(0)

(2)

No emission of ethanol is taken into account (i.e. E

(t) = 0) nor emission of

pheromone. Fig. 2.(a) shows the number of agents that turns to a “mobile” state against

the number of iterations.

A usual “S-phenomenon” [9] characterizes this evolution law. For a better illus-

tration, Fig.2.(b) shows the smoothed evolution law computed as a mean of the phe-

nomenon on 50 realizations. This ﬁrst experiment shows the viability of our model

considering simple conditions of evolution. Let us know enrich the model.

0 5 10 15 20 25

(a)

0 5 10 15 20 25

(b)

Fig.2. Illustration of the “S-phenomenon” related to the number of “mobile” agents function of

the iteration number of the process for a unique resource site where all agents (50) are located at

t = 0: (a) for one realization of the experiment, (b) averaging on 50 realizations of the experi-

ments.

4.2 Resource Attraction and Aggregating Behavior Modeling

We now want to model the resources attraction phenomenon and the aggregating be-

havior of the agents. We consider the agents are randomly located all over the area of

evolution and that ethanol and pheromones are emitted respectively by the resource

sites and the agents which have found a resource site. The corresponding emission laws

are Gaussian functions such as:

E(x, y, t) =

(t)e

−γ[(x−x

)

+(y−y

)

]

, (3)

for ethanol emission (E

(t) = µR

(t), µ being a positive value lesser than one), and

P h(x, y, t) =

P h

(t)e

−γ[(x−x

)

+(y−y

)

]

, (4)

for pheromone emission (P h

(t) = νn

(t), ν being a positive value lesser than one).

We propose to model the probability of movement by the quantity of attracting

markers in the neighborhoodof the agents. Let us deﬁne the quantity of attracting mark-

ers A(x, y, t) as a coupling between ethanol and pheromones at location (x, y) and time

A(x, y, t) = ηP h(x, y, t) + (1 − η)E

(

x, y, t) , (5)

with 0 ≤ η ≤ 1 being the coupling term. The probability to move to location

⋆

, y

⋆

) for agent a is then:

⋆

, y

⋆

) =

A(x

⋆

, y

⋆

, t)

(x,y)∈N (a)

A(x, y, t)

, (6)

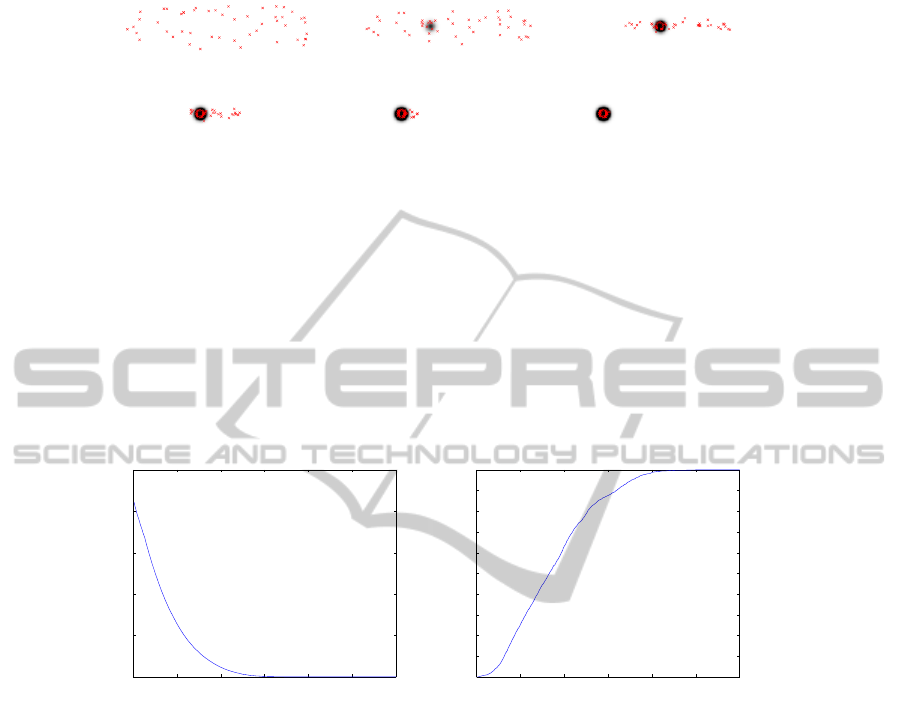
(a) (b) (c)

(d) (e) (f)

Fig.3. Illustration of Experiment 2: 50 agents are randomly dispatched all over the evolution area

(red stars) where a unique source of food is present. Evolution of the agents’ position is shown

for (a) iteration 0 of the process, (b) iteration 20, (c) iteration 60, (d) iteration 100, (e) iteration

140 and ﬁnally (f) iteration 180. The dark disk that progressively appears in the center of the

area highlights the position of the source of food, the gray level intensity is related to the level of

emitted pheromone: the more black, the more pheromone.

with N (a) being the neighborhood of agent a. In all our experiments, we consider 8-

connexity neighborhoods. Whenever an agent arrives on a resources site, it stops mov-

ing and starts emitting pheromones and consuming resources.

In Fig.3, we show the evolution of agents location as well as the pheromone levels

over time for a single run. As we can see, the agents are attracted to the resources site.

0 50 100 150 200 250 300

(a)

0 50 100 150 200 250 300

(b)

Fig.4. (a) Mean distance of the agents to the source of food function of the iteration number of

the process with η = 0.7. (b) Amount of agents on the source of food function of the iteration

number of the process (averaging on 50 realizations of the experiment)

In Fig. 4, we show (a) the mean distance of the bark beetles to the source of food

with η = 0.7 (more importance is given to pheromone emission than ethanol emission),

and (b) the amount of agents on the source of food over time t.

As we can see on Fig. 4.(a), the proposed model for ethanol and pheromone emis-

sion is compatible with a realistic modeling of the behavior of the beetles’ colony: for a

sufﬁcient number of iterations (approximately 140) all the agents have converged to the

source of food. The exponential decreasing of the plot shows a two-step process: in a

ﬁrst fast step, agents which are close from the resource site are attracted by the ethanol

emission of decomposing tree. Once they are on the resource site they then begin to

emit pheromone, attracting more and more agents. In a second step, due to the decreas-

ing of the resource, there’s a deceleration of the process since less and less ethanol is

emitted. Moreover, Fig. 4 .(b) shows the expected “S-phenomenon” related to that kind

of behavior.

Nevertheless, one limitation of this behavioral model is the insufﬁcient taken into

account of the underlying physical phenomenonrelated to pheromone and ethanol emis-

sions. More precisely, if the Gaussian laws of Eqs. (3) and (4) are realistic, they do not

integrate any temporal dynamics highlighting for instance a natural diffusion process.

And yet, this diffusion scheme will interact with the attraction process by modifying the

expected p

probability. We now propose to integrate such a diffusive property within

the model.

5 Joint SMA-PDE Modeling

We now propose to consider that ethanol and pheromones are naturally dissipated

within the atmosphere at each iteration of the evolving process characterizing the colony

of beetles. For this, the simple isotropic diffusion process is considered. This physical

phenomenon is simple but as so, remains easy to control on the contrary of more com-

plex anisotropic processes. This natural phenomenon is mathematically deﬁned by the

usual PDE of Eq. (7) also known as the “heat-equation”:

∂P h(x, y, t)

∂t

= △P h(x, y, t) =

∂

P h(x, y, t)

∂x

∂

P h(x, y, t)

∂y

(7)

with △, the Laplacian operator. If in Eq. (7), pheromone emission is considered, a

similar equation is related to natural diffusion of ethanol. Consequently, for each iter-

ation of the experiment, the initial distributions of pheromone and ethanol of Eqs. (3)

and (4) are naturally vanishing. Practically speaking, for each iteration t, Eqs. (3) and

(4) are convolved with a bidimensionnal Gaussian ﬁlter with standard deviation σ that

controls the speed of the isotropic diffusion. Iteration after iteration, the maximal am-

plitude of the pheromone emission is decreasing whereas the global spreading is made

over a larger surface of the area of simulation.

For the experiments, we set 2 different resources sites. At the beginning, all agents

are located on the ﬁrst site, which has limited resources. On the contrary, the second

site has a near inﬁnite quantity of resources. We expect the agents to quickly leave the

ﬁrst site (as in section 4.1), and converge to the second site (as in section 4.2).

Fig. 5 shows the behavior of the beetles for different iteration of the process. As it

can be noticed, after a signiﬁcant lapse of time corresponding to the random research

for food, the agents that are near the second site are attracted by the ethanol. Once these

agents ﬁnd the resource site, the emission-diffusion of pheromone makes possible a fast

convergence of all agents to the corresponding site.

Fig. 6 shows the average distance of the agents from the initial point (x

, y

), func-

tion of the iteration number of the evolving process. The global behavior of the colony

is characterized by a double “S-phenomenon”. The ﬁrst “S” corresponds to the small

pool of agents attracted by the ethanol at ﬁrst, while the second “S” corresponds to

the remaining agents attracted by the pheromones. Compared to previous experiments,

the phenomenon is slower due to the initial location of the agents. Agents ﬁrst exhaust

the food on their initial location, before they randomly move in the neighborhood. A

(a) t = 1 (b) t = 101 (c) t = 301

(d) t = 401 (e) t = 501 (f) t = 601

(g) t = 701 (h) t = 801 (i) t = 901

(j) t = 951

Fig.5. Beetles’ behavior corresponding to the joint SMA-PDA modeling proposed. σ is arbitrar-

ily set to 1.

0 100 200 300 400 500 600 700 800 900 1000

1000

2000

3000

4000

5000

6000

7000

8000

9000

10000

Fig.6. Average distance of the agents from the initial site they were localized at t = 0, function

of the iteration number of the process. Contrary to other experiments, this curve was obtained

with only one realization of the evolving process.

necessary signiﬁcant lapse of time is needed for few agents to ﬁnd the second source

thanks to the ethanol diffusion. Nevertheless, as soon as an agent is located on the new

resource site, the emission/diffusion of pheromone produces an acceleration of the con-

vergence when compared with experiment of section 4.2. Moreover, it is important to

notice that the “S-shape” of Fig. 6 was obtained with only one realization of the ex-

periment, whereas for Experiment 1 and 2, it was necessary to average the results over

50 realizations to obtain similar results. This shows the beneﬁt of integrating the un-

derlying physical phenomenon that steers the natural evolution of pheromone/ethanol

diffusion, once emitted by agents.

6 Conclusions and Perspectives

In this article, a joint MAS-PDE for the modeling of the behavior of the bark beetle’s

colonies is presented. The main originality of the proposed approach is to integrate

within a simple reactive MAS some possible physical phenomena that steers the diffu-

sion of emitted substances like pheromone or ethanol. The prospective experiments of

this work show that such a joint model could lead to more realistic simulations of the

global behavior of the colony, with no need for multiple realizations of the process. If

this study is focused on the bark beetle, clearly identiﬁed since 2005 as a pest insect,

extensions to ant-like insects are straight forward. The next experiments will consist in

(i) improving the MAS by a managing of the “birth” and “death” of the beetles, but

also of the funding of new colonies by females, and(ii), in considering the possibility

to integrate more complex diffusion processes, like anisotropic ones, in order to take

into account the structure of the bark beetle’s nest within trees (galleries), and natural

perturbations like wind.

References

1. Berryman, A. A., Millstein, J. A.: Population analysis system. Pullman edn., Washington

(1994) Version 4.0.

2. Ferber, J.: Multi-Agent Systems: An Introduction to Distributed Artiﬁcial Intelligence.

Addison-Wesley (1999)

3. Demazeau, Y.: From interactions to collective behavior in agent-based systems. In: Proceed-

ings of the First European Conference on Cognitive Science. (1995) 117–132

4. Deneubourg, J., Goss, S.: Collective patterns and decision-making. 1 (1989) 295–311

5. Sun, R.: Cognitive Science Meets Multi-Agent Systems: A Prolegomenon. Phylosophical

Psychology 14 (2001) 5–28

6. Weyns, D., Parunak, H., Michel, F., Holvoet, T., Ferber, J.: Environments for Multiagent

Systems State-of-the-Art and Research Challenges. In: Proceedings of E4MAS. (2004) 1–47

7. Bentz, B.: Climate Change and Bark Beetles of the Western United States and Canada: Direct

and Indirect Effects. BioScience 8 (2010) 602–613 doi:10.1525/bio.2010.60.8.6.

8. Robins, J.: Bark Beetles Kill Millions of Acres of Trees in West. New York Times, 17

November (2008)

9. Langlois, P., Daud´e, E.: Concepts et mod´elisations de la diffusion g´eographique. Cybergeo:

European Journal of Geography 364 (2007) http://www.cybergeo.eu/index2898.html