Autonomous Wheelchair for Patients with Severe Motor Disabilities
Alfredo Ch
´
avez
1
, H
´
ector Caltenco
2
, Kim Dremstrup
1
and Alvaro Fuentes Cabrera
1
1
Department of Health Science and Technology, Aalborg University, Aalborg, Denmark
2
Certec, Dept. of Design Sciences, Lund University, Lund, Sweden
Keywords:
Sensor Fusion, Autonomous Wheelchair, Laser, Occupancy Grids, Localization, Nonlinear Control, Input-
Output Linearization, Path Planning.
Abstract:
This paper presents the design and implementation of a control strategy for an autonomous wheelchair to
assist individuals suffering from severe motor disabilities. The user is presented with a pre-generated map of
a known area (e.g. home, office) displayed on a computer screen, on which the location of the wheelchair is
shown. Using a specially design man-machine interface the user can select the desired point to be transported
to. After the the desired point has been selected on the map, the control algorithm calculates the path and
transports the user to the destination, avoiding any obstacles on its way. A Bayesian estimation method, which
takes into account the uncertainty inherent in the sensor measurements, is used to fuse the sensory information
obtained from a laser, and to generate and update the occupancy grid map. The proposed system uses data from
a probabilistic laser map to feed a Kullback Leiber Divergence KLD localization algorithm and path planning
based on the solution of the Laplace’s equation. The system described in this manuscript is simulated in
Matlab using actual measurements from a laser mounted on a mobile robot.
1 INTRODUCTION
Several electrical powered wheelchairs with modu-
lar architecture to assist mobility of disabled per-
sons are available in the market (Edlich et al., 2004).
While users with remaining hand functionality of-
ten use a joystick to control direction and speed of
the wheelchair, many need different control inter-
faces that suit their needs. Users with severe upper-
limb mobility impairments, such as spinal cord injury
(SCI), have to rely on alternative control interfaces
based on head (Christensen and Garcia, 2003), chin
(Guo et al., 2002), eye (Agustin et al., 2009) or tongue
(Huo and Ghovanloo, 2010; Lund et al., 2010) move-
ments. Interfaces controlled with brain activity, com-
monly called brain-computer interfaces (BCI) (Reb-
samen et al., 2007), have also been developed to as-
sist users suffering from total motor paralysis, e.g. ad-
vanced states of amyotrophic lateral sclerosis (ALS).
However most of these interfaces require high levels
of concentration for navigating in environments with
many obstacles, fixing the eyes on the screen (eye
trackers) or holding the tongue in certain position for
long time (tongue interfaces). Driving the wheelchair
and doing activities that require the use of eyes, head
or tongue at the same time might not be possible.
Another approach to augmentative mobility of
disabled persons is the use of an autonomous
wheelchair, which typically consists of either a stan-
dard powered wheelchair mounted with a computer
and a collection of sensors or a mobile robot specially
modified for the transportation of persons, (Blatt
et al., 2008). The level of autonomy of the wheelchair
depends on the complexity of the sensor fusion, map
making, localization, path planing and control mod-
ules. The more advanced the modules are, the less
interaction they should require from the user to con-
trol direction and speed movement in order to ensure
a collision-free travel, e.g. avoiding obstacles, like
furniture, passing through doorways, or an accurate
navigation to the desired location (Tonin et al., 2010).
Adding low-level autonomy to the wheelchair, while
still mantaining high level control from the user, can
be advantageous in many environments. Therefore,
an autonomous wheelchair should require from regu-
lar to as little physical contribution as possible from
the user, while still providing robust, safe and reliable
mobilization.
Previous research on autonomous wheelchair
has focused on different levels of autonomy, e.g.,
Miller and Slack (Vlassis et al., 1996) developed
a wheelchair that assist the user in avoiding obsta-
93
Chávez A., Caltenco H., Dremstrup K. and Fuentes Cabrera A..
Autonomous Wheelchair for Patients with Severe Motor Disabilities.
DOI: 10.5220/0004362700930101
In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2013), pages 93-101
ISBN: 978-989-8565-71-6
Copyright
c
 2013 SCITEPRESS (Science and Technology Publications, Lda.)

cles, going to pre-designated places and maneuver-
ing through narrow or crowded areas, making use of
a variation of Dijkstra’s algorithm on top of a topo-
logical map for path planing and obstacle avoidance.
Civit et al (Civit-Balcells et al., 2002) presented a sys-
tem that implemented recorded trajectory playback,
while also providing computer assisted navigation to
the user. Both systems previously described were im-
plemented in a powered wheelchair, where users pro-
vided input using a joystick. This interaction method
might be notoptimal for people with sever motor im-
pairments. Coelho and Nunes (Coelho and Nunes,
2004) proposed an algorithm for path following con-
trol, based on a destination point paradigm, but lacks
map making, path planning and localization.
In the system described in this study, the user can
input the coordinates of the destination on a map of
the known environment using a regular pointing de-
vice or assistive computer interface, in this paper we
used an inductive wireless tongue-computer interface
(Lund et al., 2010) to select the desire location on
the map, previously built by the sensors. We have
also included in the present study a global localiza-
tion and a path planning module to generate a refer-
ence to the control input and estimate the actual pose
of the wheelchair respectively. The proposed system
would be able to autonomously transport the user to
a desired location from a starting point in a known
environment.
2 METHODS
The control algorithm described in this section has
been designed to work using one input from the user,
that is a destination point. When the system is turned-
on the first task it performs is to display the map of
the environment. Then, using the data from the laser,
the system localizes the wheelchair on the map. The
user is then asked to choose the desired destinationon
the map of the known environment, through the use
of any pointing device or assistive computer inter-
face. Then, armonic potential field path planing (Mi-
tra, 2008; Connolly, 1997) is performed. Then, lo-
calization of the wheelchair in the previously gener-
ated map of the environment to be navigated using the
Kullback Leibler Divergence (KLD) sampling (Her-
shey and Olsen, 2007). The control of the trajectory is
based on input-output state feedback control, method
which has been chosen due to the fact that the system
has both holonomic and non-holonomic constraints,
making the system not fully state feedback lineariz-
able (Coelho and Nunes, 2003; Sarkar et al., 1994;
Nijmeijer and Van der Schaft, 1990).
2.1 Sensor Fusion and Map Making
During the functioning of an autonomous wheelchair
the uncertainty inherited in laser sensor data readings
must be interpreted by means of a probabilistic sensor
model and fused into a probabilistic occupancy map
grid, where the recursive Bayesian method is used to
update the probabilistic map (Elfes, 1989).
P
o
=
P
o
s
P
o
m
P
o
s
P
o
m
+ (1 − P
o
s
)(1 − P
o
m
)
(1)
where
• P
o
m
and 1−P
o
m
are the prior probabilities that a cell
is occupied and empty respectively.existing map.
• P
o
s
is the conditional probability that a sensor
would return the reading given the state of the cell
being occupied.
• P
o
is the conditional probability that a cell is oc-
cupied based on the previous sensor readings.
A new sensor reading introduces additional infor-
mation about the state of the cell C
i, j
. This informa-
tion is obtained by the sensor model P
o
s
. And, it is
combined with the most recent probability estimate
stored in the cell P
o
m
by means of the Bayes’ rule
to give a new estimate P
o
. The initial map’s prior
cell probabilities are initialized to P
o
m
= 1 − P
o
m
= 0.5
∀ C
i, j
.
2.2 Localization within the Map
The localization of the wheelchair within the map is
done using the KLD algorithm, which is a variant of
the MCL algorithm in the sense that it adapts the num-
bers of samples over time, (Thrun, 2002).
The KLD implementation (algorithm 1) takes as
inputs the previous sample set (X
t−1
), the map, the
most recent control odometry data (U
t
) and laser
measurements (Z
t
). It also includes statistical error
bounds ε and δ. In contrast, it ensures the actual sam-
ple set (X
t
) and the best state estimate (x
est
).
Lines 1 through 2 of algorithm 1 initialize X
t
, and
particle thresholds M and M
x
. Initially each bin b in
the histogram H is set to empty (lines 3 through 5).
In line 7, the particle is drawn in a probabilistic way
according to the weights of the particles w
i
t−1
. The
outcome is a single particle, which is then predicted,
weighted and inserted in the new sample set (lines 8-
10). The core of the KLD-sampling is implemented
in lines 11 through 18. Line 11 examines whether the
new particle falls into an empty bin in the histogram.
If it does it, then the number of non-empty bins (k) is
incremented and then the bin is set to non-empty bin.
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
94

Therefore, the number k represents the number of his-
togram bins filled with at least one particle. M
x
gives
the number of particles needed, based on the number
k and the statistical error bounds ε and δ. These values
are available in standard statistical tables. The algo-
rithm main loop ends when M exceeds M
x
and M
min
.
Lines 20 through 23 normalize the weights to ensure a
probabilistic distribution. Lines 23 through 24 select
the best state estimate x
est
, (Thrun, 2002).
Algorithm 1: KLD-Sampling.
Require: X
t−1
, U
t
, Z
t
, map, ε, δ
Ensure: X
t
, x
est
1: X
t
= 0
2: M = 0, M
x
= 0, k = 0
3: for all b in H do
4: b =empty
5: end for
6: while M < M
x
AND M < M
min
do
7: draw a particle i with a probability w
[i]
t−1
8: X
[M]
t
= sample motion model(U
t
, x
i
t−1
)
9: w
[M]
t
= measurement model(z
t
, x
M
t
, map)
10: X
t
= X
t
+ ⟨X
M
t
, w
M
t
⟩
11: if x
M
t
falls into an empty bin b then
12: k = k + 1
13: b =non-empty bin
14: if k > 1 then
15: M
x
:=
k−1
2ε

1 −
2
9(k−1)
+

2
9(k−1)
z
1
− δ

3
16: end if
17: end if
18: M = M + 1
19: end while
20: W
total
=
∑
M
i=1
w
[i]
t
21: for i = 1 to M do
22: w
[i]
t
=
w
[i]
t
W
total
23: end for
24: index = max(W
total
)
25: x
est
= X
t
(index)
2.3 Path Planning
To ensure free collision path planning, the occu-
pied area (shown as white surface on the maps) has
been dilated in 20cm from the contour (Gonzalez and
Woods, 2002). Then, the planner finds a suitable path
based on a selected destination point. Thus, for plan-
ning purposes the grid elements that represent bound-
ary conditions like the obstacles and goal are held
fixed to one and zero respectively. In the following
the path planning algorithm is described.
Previous studies in robotics have used harmonic
functions to solve the Laplace’s equation for robot
path planning (Mitra, 2008; Connolly, 1997). A har-
monic function ϕ on a domain Ω ⊂ R
n
is a function
that satisfies Laplace’s equation, (Connolly, 1997).
∆
2
ϕ =
n
∑
i=1
∂
2
ϕ
∂x
2
i
= 0 (2)
The solution of Laplace’s equation yields to equa-
tion (3).
ϕ
i, j
=
1
4
(ϕ
i+1, j
+ ϕ
i−1, j
+ ϕ
i, j+1
+ ϕ
i, j−1
) (3)
If ϕ satisfies Laplace’s equation, then any grid cell
C
i, j
that correspond to ϕ
i, j
in the domain Ω, is the av-
erage of the cell’s values at four surrounding points.
This method is an iterative process that ends when
there is no change of any cell grid from one iteration
to the next. The algorithm creates smooth collision-
free paths and does not suffer from local minima as
the potential field algorithm does, (Lai et al., 2007;
Connolly, 1997). 2 shows the algorithm.
Algorithm 2: Path planning using Laplace’s equation.
Require: ϕ
0
i, j
{The initial map };
Ensure: ϕ
n+1
i, j
{Harmonic functions};
1: ϕ
i, j
⇐ 1 {Obstacles (i, j) are fixed to 1};
2: ϕ
i, j
⇐ 0 {Goal position (i, j) is fixed to 0};
3: while ϕ
n+1
i, j
̸= ϕ
n
i, j
do
4: ϕ
n+1
i, j
⇐
1
4
(ϕ
n
i+1, j
+ ϕ
n
i−1, j
+ ϕ
n
i, j+1
+ ϕ
n
i, j−1
)
5: end while
3 MODELING AND CONTROL
Consider a nonholonomic differential drive
wheelchair (front drive wheels) subjected to m
constraints and n generalized coordinates (q), where
m < n is assumed. A geometric model is shown in
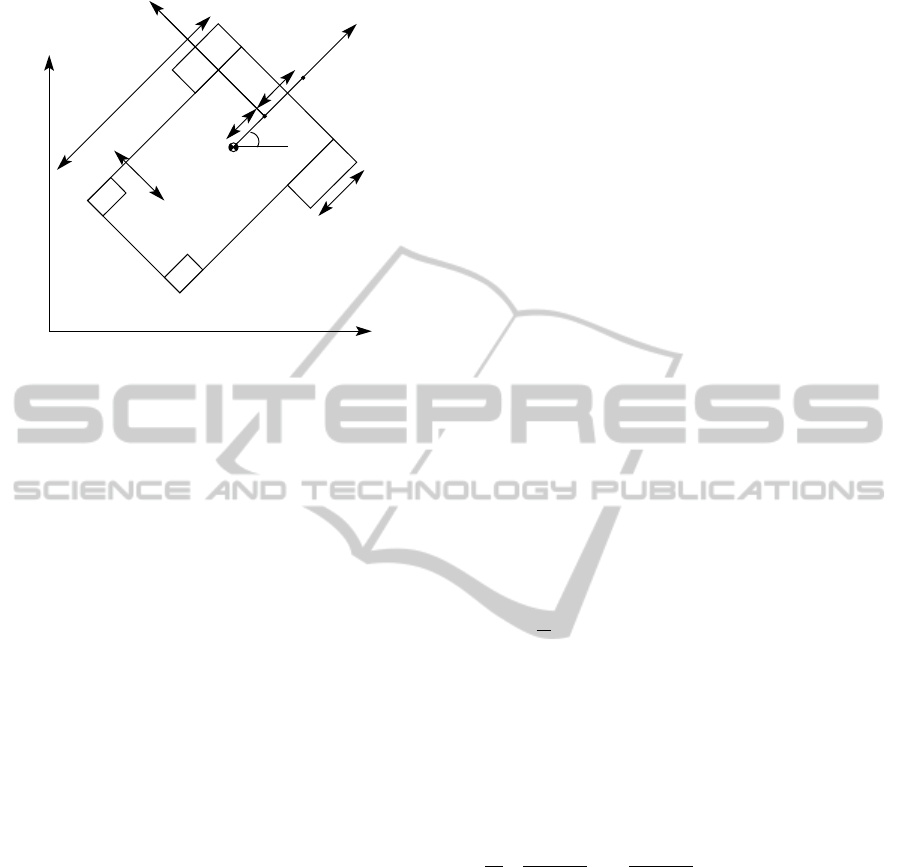
Figure 1, where;
F
A
, fix robot frame (x
1
, x
2
). F
W
world reference
frame (x, y). CM, center of mass. P
c
, center of mass
(x
c
, y
c
). P
l
, virtual point (x
l
, y
l
). P is an intersection
point between the driving wheel axis and the geome-
try axis of symmetry. b, distance between the center
of each wheel and the geometry axis of symmetry. a,
the length of the platform. d, distance from P
c
to P.
L, distance from P to P
l
. r, radius of each wheel. w
r
,
right wheel. w
l
, left wheel. α, the angle from CM to
the center of the wheel. θ, angle of rotation.
AutonomousWheelchairforPatientswithSevereMotorDisabilities
95

θ
P
l
x
d
P
a
x
1
y
P
c
CM
L
x
2
b
F
A
F
W
2r
w
r
w
l
cw
cw
Figure 1: Differential drive wheelchair geometry. A fixed
local frame F
A
is attached to the mobile robot and moving
with respect to a world reference frame F
W
. θ is the angle
of rotation around the center of mass CM and with respect
to F
W
. The robot moves along x
1
and perpendicular to the
driving wheel axis.
3.1 Kinematic Model
Two constraints are imposed to the kinematic model.
a) Rolling without slipping, which means that the lin-
ear velocity of the wheel at the contact point must be
zero, (Campion et al., 1996). b) No lateral movement
constraint assumes that the wheel’s orthogonal veloc-
ity components are zero, (Campion et al., 1996).
Equations (4) to (6) are the constraints imposed to
the fixed wheels of the system with respect to P
c
.
˙y
c
cosθ − ˙x
c
sinθ +
˙
θd = 0 (4)
˙x
c
cosθ + ˙y
c
sinθ + b
˙
θ − r
˙
ψ
r
= 0 (5)
˙x
c
cosθ + ˙y
c
sinθ − b
˙
θ − r
˙
ψ
l
= 0 (6)
The m constraints are in the form C(q, ˙q), with k
holonomic constraint and m − k nonholonomic con-
straints, all of which can be written in the form,
A(q) ˙q = 0 (7)
With
A(q) =


−sinθ cosθ d 0 0
−cosθ −sinθ −b r 0
−cosθ −sinθ b 0 r


(8)
˙q =

˙x
c
˙y
c
˙
θ
˙
ψ
r
˙
ψ
l

(9)
Some remarks about C(q, ˙q) can be stated as fol-
low; if C(q) it can be integrated, is a holonomic con-
straint and if C( ˙q) can not be integrated, is a nonholo-
nomic constraint.
From the mechanical system given by equation
(7), Let S
i
(q) = [s
1
, ·· · , s
n−m
]
T
be a set of smooth
(continuously differentiable) and linear independent
vector fields in the null space of A(q), (N(A)),
such that, A(q)S
i
(q) = 0, i = 1, ·· · , n − m. Hence,
S
i
(q) = ˙q. Now it is possible to define (n −m) veloci-
ties η(t) = [η
1
, ·· · , η
n−m
]
T
such that for all t, (Coelho
and Nunes, 2003).
˙q = S(q)η(t) (10)
Equation (10) represents the kinematic model of
a mechanical system, where S(q) is a Jacobian map-
ping matrix from R
(n−m)
→ R
n
. In other words, it
converts velocities from a mobile entity to velocities
in a Cartesian system.
A Jacobian matrix S(q), which satisfies the rela-
tion A(q)S(q) = 0, must be computed and finally a
velocity vector η is stated. The computation of N(A)
turns out in equation (11), whereas, the velocity vec-
tor results in η = [η
1
, η
2
]
T
= [
˙
ψ
1
,
˙
ψ
2
]
T
.
S(q) =





c(bcosθ + dsinθ) c(bcosθ − dsinθ)
c(bsinθ − dcosθ) c(bsinθ + dcosθ)
c −c
1 0
0 1





(11)
With c =
r
2b
.
3.2 Dynamic Model
The Lagrangian formalism to holonomic and non-
holonomic systems has been selected to develop the
dynamic equations of motion (Bloch, 2003; Gold-
stein, 1980).
d
dt

∂L(q, ˙q)
∂ ˙q

−
∂L(q, ˙q)
∂q
= M
I
(q) ¨q +V (q, ˙q)
= B(q)τ − A
T
(q)λ
(12)
L(q, ˙q) = T (q, ˙q) − W (q), the Lagrangian of the
system. M
I
∈ R
n×n
, the inertia matrix. V (q, ˙q) ∈
R
n×n
, the centripetal and coriolis matrix. A
T
(q),
the Jacobian transport matrix of the constraint ma-
trix. B(q) ∈ R
n×(n−m)
, the input transformation ma-
trix. τ ∈ R
(n−m)
, an input torque vector. λ ∈ R
m
,
the undetermined Lagrangian multipliers. It is as-
sumed that the differential wheelchair is moving only
in a horizontal plane, therefore the potential energy
remains constant and can be neglected from the La-
grangian multiplier. The kinetic energy of a dif-
ferential wheelchair with respect to P
c
is stated as,
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
96

T =
1
2
˙
ξ
T
R
T
MR
˙
ξ +
1
2
˙
ψ
T
I
wm
˙
ψ. With;
˙
ξ = [ ˙x
c
, ˙y
c
,
˙
θ
c
]
T
,
˙
ψ = [
˙
ψ
1
,
˙
ψ
2
]
T
, I
wm
= [I
w
, 0; 0, I
w
],
M =


M
1
0 M
2
0 M
1
M
3
0 0 M
4


R =


cosθ sinθ 0
−sinθ cosθ 0
0 0 1


Where:
M
1
= M
2
=
1
2

M
T
+2m

, M
3
= ml
∑
2
i=1
cos

α
i
+
θ

, M
4
=
1
2

I
T
+ 2ml
2
+ I
w

.
The dynamic model is obtained by replac-
ing T into the left expression of equation
(12), with; ¨q = [ ¨x
c
, ¨y
c
,
¨
θ,
¨
ψ
r
,
¨
ψ
l
]
T
V (q, ˙q) =
[−2m
w
d
˙
θ
2
cosθ, −2m
w
d
˙
θ
2
sinθ, 0, 0, 0]
T
τ = [τ
r
, τ
l
]
T
B(q) = [0, 0; 0, 0; 0, 0; 1, 0;0, 1]
M
I
(q)=





M
I
1
0 M
I
2
0 0
0 M
I
1
M
I
3
0 0
M
I
4
M
I
5
M
I
6
0 0
0 0 0 I
w
0
0 0 0 0 I
w





(13)
Where, M
I
1
= M
T
+ 2m
w
, M
I
2
= −2m
w
dsinθ,
M
I
3
= 2m
w
dcosθ, M
I
4
= −2m
w
dsinθ, M
I
5
=
2m
w
dcosθ, M
I
6
= I
T
+2m
w
l
2
+I
w
. τ
r
and τ
l
, the right
and left torques. M
T
, the mass.
¨
ψ
r
and
¨
ψ
l
, the right
and left angular accelerations.
A dynamic mapping function f : τ →
˙
η is obtained
by elimination of the Lagrangian multipliers from
(10), where, f
1
= S
T
M
I
S and f
2
= S
T
M
I
˙
Sη + s
T
V .
˙
η = − f
−1
1
f
2
+ f
−1
1
τ (14)
Choosing the state space variable x = [q
T
η
T
]
T
and
from (10) and (14), the kinematic and dynamic sys-
tems can be arranged into a state representation.
˙x =

Sη
− f
−1
1
f
2

+

0
f
−1
1

τ
(15)
3.3 Input-Output Linearization
The system in turn is not fully input state lineariz-
able, it may be input-output linearizable if a proper set
of output equations are chosen, (Coelho and Nunes,
2003).
A state diffeomorphism transformation z = T (x)
and x = T
−1
(z), will bring the system in a normal
form with external and internal parts respectively,
making the system partially linearizable.
External and internal variables are visible and hid-
den to the output respectively. Moreover, a control
law will bring the external part of the normal system
into a lineal one. The relative degree of the system
may tell the number of outputs equations must be cho-
sen for a specific system.
The state representation stated in equation (15)
is arranged in a general nonlinear form by choosing
a nonlinear feedback τ = f
1
u + f
2
. With; f (x) =
[S(q)η, 0]
T
and g(x) = [0, I]
T
˙x = f (x) + g(x)u (16)
y = h(x) (17)
Since, there are two inputs to the system u =
[u
1
, u
2
]
T
two output equations must be chosen, y =
[y
1
, y
2
]
T
= h(q) = [h
1
(q), h
2
(q)]
T
. For trajectory
tracking control system, two output equations are
chosen based on the coordinates of the virtual point
P
l
.
y =

y
1
y
2

= h(q) =

h
1
(q)
h
2
(q)

=

x
c
+ (d + L)cosθ
y
c
+ (d + L)sinθ

(18)
In order to obtain the relative degree of the system,
the output y is derivate until it meets the input u.
˙y = Φ(q)η
¨y =
˙
Φ(q)η + Φ(q)u
(19)
The output y has been derivate twice before it has
encountered the input u, therefor is verified that the
relative degree of the system is ρ = 2.
Φ(q) is the decoupling matrix and defined as
Φ(q) = J
h
(q)S(q) and J
h
=
∂h(q)
∂q
∈ R
(n−m)×n
as the
Jacobian Matrix.
A state variable transformation vector will bring
the system into an input-output linearizable one
(Sarkar et al., 1994; Yun et al., 1992).
z = T(x) = [z
1
, z
2
, |z
3
, z
4
, |z
5
]
T
=
[h(q), |L
f
h(q), |
˜
h(q)]
T
= [h(q), |Φ(q)η, |
˜
h(q)]
T
.
Where
˜
h(q) ∈ R
m
is a vectorial function such that
[J
T
h
, J
T
˜
h
] is a full row rank, (Sarkar et al., 1994; Yun
et al., 1992). The system under the new state variable
transformation vector T(x) is characterized by
˙z = [˙z
1
, ˙z
2
, |˙z
3
, ˙z
4
, |˙z
5
]
T
=

z
3
, z
4
, |

˙
Φ(q)η +
Φ(q)u

, |

J
˜
h
Sη(J
h
S)
−1

[z
3
, z
4
]
T

T
.
The observable part of the system ˙z =
[˙z
1
, ˙z
2
, ˙z
3
, ˙z
4
]
T
, is arranged as
˙z = A
c
z + B
c
Φ(q)

u −

− Φ
−1
(q)
˙
Φ(q)η

(20)
Where A
c
and B
c
are controllable matrices.
Choosing a state feedback control law of the form
u = α(q) + β(q)ν, with α(q) = −Φ
−1
(q)
˙
Φη, β(q) =
Φ
−1
(q) and γ(q) = β
−1
(q) = Φ(q).
AutonomousWheelchairforPatientswithSevereMotorDisabilities
97

u = −Φ
−1
(q)
˙
Φη + Φ
−1
(q)ν (21)
Equation (21) brings the system (20) into a linear
one, ˙z = A
c
z + B
c
ν.
The kinematic and the dynamic models, the non-
linear feedback, the nonlinear state feedback con-
trol law and the linear state transformation variables
are summarized in the following: ˙q = S(q)η,
˙
η =
f
−1
1
f
2
+ f
−1
1
τ, τ = f
1
u + f
2
, u =
˙
Φ
−1

ν − Φη

, z
1
=
h
1
(q). z
2
= h
2
(q), z
3
= Φ
1
(q)η, z
4
= Φ
2
(q)η. Φ
1
(q)
and Φ
1
(q) are the decoupling matrix members.
4 THE COMPLETE SYSTEM
The complete system, composed of the parts de-
scribed in previous sections, is depicted in Figure
2. The Map making block is responsible for fusing
and generating a probabilistic map of the environment
based on laser readings. The path planning block has
to generate a smooth path from the start to the goal.
Once the path is generated, it is used as a reference,
which is compared with the output from the system.
The difference between the path and the reference is
an error, which will be used as the input to the con-
trol. Meanwhile, the localization block together with
the output from the actuators are used to generate the
output signals which have to be compared with the
reference input. The control block, whose dynamic
equations have been discretized by means of second
order Runge-Kutta method (Mathews, 1992), gener-
ates the control signals to the actuators which will fol-
low a specific path. In order to assess the performance
of the complete system, 10 simulations have been car-
ried out in Matlab, using different starting and desti-
nation points, including transit through doorways and
narrow paths, as shown in Figure 5.
+
+
−
−
Map
interface
ALS
Path
Planning
Actuators
control
System
Control
Tongue
interface
making
η
η
m
z
r
H

q, η

Localization
Figure 2: Block diagram of the complete system. The path
planning is achieved after a destination point is selected on
the map, this action produces a reference input to the control
module, then the control path tracking strategy is applied to
give the right commands to the actuators.
5 RESULTS
All results shown in this section correspond to the
simulation of the system, performed in Matlab using
data from a SICK 200 laser to build the map. A total
of 30 measurements along a trajectory have been car-
ried out by a mobile robot. In each measurement the
laser scans a total of 361 readings distributed along
180
o
. The black area in the map represents free space
C
f ree
while the white area represents occupied space
or C-obstacle-region CB
region
.
5.1 Localization
For the first laser sampling, 3 iterations of the KLD
algorithm were performed, while only one iteration
was performed for the rest laser samplings as is shown
in Figure 3.
• Figure 3(a) shows the result of the algorithm in the
firsts laser measurement after one iteration, where
the red circle is the true pose, the green cross is
the best estimate pose calculated by the algorithm,
and the blue crosses are random particles that re-
main after the first iteration.
• Figure 3(b) shows the result of the algorithm that
is still in the first laser measurement, e.g. the mo-
bile entity has not moved at all. The algorithm has
performed three iterations, where random parti-
cles has been eliminated and the ones that remain
are concentrated around the best estimate.
• Figures 3(c) and (d) shows the results for the 10
th
and 20
th
laser samplings after 1 iteration.
It can be seen that the KLD algorithm accurately
tracks and localizes the mobile entity in the configu-
ration space of the map as shown in Figure 4. Table 1
shows the true poses for different number of iterations
as well as the best estimate poses in [x, y] coordinates.
Table 1: Comparison between true pose and best estimate
using KLD.
N
o
(x, y) cm
Iterations true pose Best estimate Error
1 (225, 250) (220, 265) 15.8
3 (225, 250) (195, 265) 33.5
10 (585, 540) (590.3, 527.8) 13.2
20 (540, 910) (553.8, 908.8) 13.6
5.2 Motion Planning
Motion planning simulation based on the solution of
Laplace’s equation, corresponding to simulation 1 in
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
98

(1)
(2)
(3)
(4)
Figure 3: (a) shows the result of the algorithm for the first
laser sampling after 1 iteration. (b) result of the algorithm
for the first laser sampling after 3 iterations. (c) result of
the algorithm for the 10
th
laser sampling after 1 iterations.
(d) result of the algorithm for the 20
th
iteration after 1 iter-
ations.
Figure 4: Comparison between the true poses and best esti-
mates.
table 2, is shown in Figure 5. It also depicts a start
point (blue circle) and a destination point (red square).
5.3 Control Simulation
Input-output state feedback nonlinear control path
following for a cosine reference path is depicted in
Figure 6. Where, y
1
, y
2
represents the coordinates of
the virtual point P
l
and x
c
, y
c
represents the coordi-
nates of the center of mass.
5.4 System Simulation
Table 2 shows the Mean Square Error between the
reference input and the estimation of the localization
Figure 5: Configuration space created by dilation of the oc-
cupied spaces. The blue circle represents the start point con-
figuration. The red square represents the the goal configu-
ration coordinates chosen either by a tongue or a BCI in-
terfaces. A smooth path (τ) in the free configuration space
(C
f ree
) is shown.
0 2 4 6 8 10
−1.5
−1
−0.5
0
0.5
1
1.5
position [x,y]
x [m]
y [m]
y1,y2
xc,yc
reference
Figure 6: Shows the path following control strategy for a
cosine path. The robot pose is at the origin of the coordinate
system, then it reaches the path reference and follow it.
algorithm (MSErc), and the Mean Square Error be-
tween the reference input and the control tracking
(MSEre) for the 10 simulations performed in Mat-
lab. The mean and standard deviation of MSErc and
MSEre are displayed in the bottom rows.
Figure 7 shows the nonlinear control path corre-
sponding to simulation 1. The reference input is rep-
resented as a solid line, and the output from the con-
trol algorithm is represented as a dash line. Figure
8 depicts the estimation localization tracking corre-
sponding to simulation 1 in table 2. The reference in-
put is represented as a solid line, whereas the coordi-
nates from the localization algorithm are represented
as a dashed line.
6 CONCLUSIONS
The simulation of an autonomous wheelchair has
been described in the present study, including mod-
ules for sensor fusion, map making, localization, path
AutonomousWheelchairforPatientswithSevereMotorDisabilities
99

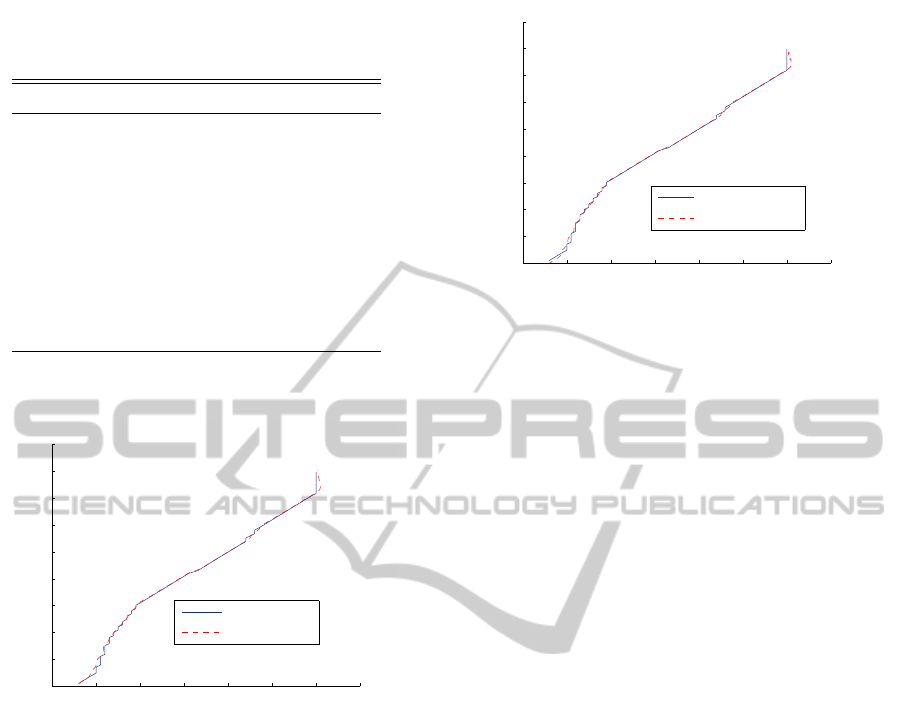
Table 2: Mean Square Error between the reference input and
estimation of the localization algorithm (MSErc), and be-
tween the reference input and the control tracking (MSEre)
for all 10 trajectory simulations described in .
Simulation MSErc [cm
2
] MSEre [cm
2
]
1 6 11
2 3.7 13.1
3 3.8 5.1
4 3.9 5.1
5 5.7 8.6
6 11.5 28.1
7 6.5 21.7
8 5.2 3.2
9 6 8.2
10 5.5 8.5
Mean 5.8 11.2
Std 2.2 7.9
200 250 300 350 400 450 500 550
200
250
300
350
400
450
500
550
600
650
X [cm]
Y[cm]
reference
control
Figure 7: Control simulation, the reference input is repre-
sented as a solid line, the control trajectory tracking is rep-
resented as a dash line.
planing and control strategy.
The KLD localization algorithm considerably re-
duced the number of particles during the localiza-
tion tracking after 3 iterations (Figure 4) . In table 1
can be observed that the best pose estimation for the
first laser sampling, which represent the wheelchair
in still position (initialization), has an accuracy error
of 15.8cm and 33.5cm for 1 and 3 iterations respec-
tively. For the 10
th
and 20
th
laser samplings, which
represents the position of the wheelchair, the accu-
racy errors are 13.2 and 13.6 cm respectively. The
errors corresponding to the wheelchair in movement
are smaller than the dilation of the occupied spaces
(20cm), which ensures a free collision trayectory.
Statistical analysis of ten trajectory simulations of
the system showed mean squared errors of 11.5cm
2
and 28cm
2
for localization MSErc and tracking
MSEre respectively, what ensures accurate navigation
due to the 20 cm dilation of the occupied spaces.
200 250 300 350 400 450 500 550
200
250
300
350
400
450
500
550
600
650
X [cm]
Y [cm]
reference
localization
Figure 8: Estimation simulation, the reference input is rep-
resented as a solid line, the estimated localization trajectory
tracking is represented as a dash line.
Results have been presented from a computer
simulation of an autonomous differential drive
wheelchair, using its kinematic and dynamic mod-
els. Accurate control of the real wheelchair would
require attentions for more practical issues, e.g. non-
holonomic constraints, such as for instance the influ-
ence of tyres etc. Stability of internal variables can
be analyzed by zero dynamics of the system, (Khalil
and Grizzle, 2002). This would be specially useful af-
ter having added the real-wheelchair non-holonomic
constraints and other necessary control parameters.
However, the simulation results in this paper have
shown the feasibility of using the proposed system for
an autonomous wheelchair control.
Several interfaces exist that provide users with se-
vere mobility impairments the possibility to control a
wheelchair, e.g., using the chin, mouth, tongue, eyes
or even brainwaves. However most of these inter-
faces require high levels of concentration, or interfere
with other parallel activities that could be done while
driving the wheelchire, such as looking around the
environment (gaze trackers, head or chin joysticks),
talking (tongue-interfaces), or even getting distracted
(brain-computer interfaces). Therefore, driving the
wheelchair and doing activities that require the use
of eyes, head or tongue at the same time might dif-
ficult. This work, is the first step for a combina-
tion of low-level autonomous control, and high-level
user input, based on a single command from the user,
to provide augmentative mobilization to individuals
with severe motor impairments, such as high-level
spinal cord injury or advanced states of amyotrophic
lateral sclerosis. Such persons could use e.g. the
ITCS(Andreasen Struijk et al., 2009) or a BCI (Cabr-
era and Dremstrup, 2008), in order to successfully
choose destination points and override autonomous
driving when needed.
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
100

REFERENCES
Agustin, J. S., Mateo, J. C., Hansen, J. P., and Villanueva,
A. (2009). Evaluation of the potential of gaze input
for game interaction. PsychNology Journal, 7(2):213–
236.
Andreasen Struijk, L. N. S., Lontis, E. R., Bentsen, B.,
Christensen, H. V., Caltenco Arciniega, H. A., and
Lund, M. E. (2009). Fully integrated wireless induc-
tive tongue computer interface for disabled people. In
Proceedings of the 31st Annual International Confer-
ence of the IEEE Engineering in Medicine and Biol-
ogy Society, pages 547–550.
Blatt, R., Ceriani, S., Dal Seno, B., Fontana, G., Matteucci,
M., and Migliore, D. (2008). Brain control of a smart
wheelchair. In 10th International Conference on In-
telligent Autonomous Systems.
Bloch, A. (2003). Nonholonomic mechanics and control.
Springer Verlag.
Cabrera, A. and Dremstrup, K. (2008). Steady-State Vi-
sual Evoked Potentials to drive a Brain Computer In-
terface. Technical report, Aalborg University. Depart-
ment of Health Science and Technology Aalborg.
Campion, G., Bastin, G., and Dandrea-Novel, B. (1996).
Structural properties and classification of kinematic
and dynamic models of wheeled mobile robots.
Robotics and Automation, IEEE Transactions on,
12(1):47–62.
Christensen, H. and Garcia, J. (2003). Infrared Non-Contact
Head Sensor, for Control of Wheelchair Movements.
Assistive Technology: From Virtuality to Reality, A.
Pruski and H. Knops (Eds) IOS Press, pages 336–340.
Civit-Balcells, A., Diaz Del Rio, F., Jimenez, G., Sevillano,
J., Amaya, C., and Vicente, S. (2002). SIRIUS: Im-
proving the maneuverability of powered wheelchairs.
In Control Applications, 2002. Proceedings of the
2002 International Conference on, volume 2, pages
790–795. IEEE.
Coelho, P. and Nunes, U. (2003). Lie algebra applica-
tion to mobile robot control: a tutorial. Robotica,
21(05):483–493.
Coelho, P. and Nunes, U. (2004). Path following control
of a robotic wheelchair. IAV2004-PREPRINTS 5th
IFAC/EURON Symposium on Intelligent Autonomous
Vehicles Instituto Superior T
´
ecnico, Lisboa, Portugal
July 5-7, 2004.
Connolly, C. (1997). Harmonic functions and collision
probabilities. The International Journal of Robotics
Research, 16(4):497.
Edlich, R., Nelson, K., Foley, M., Buschbacher, R., Long,
W., and Ma, E. (2004). Technological advances in
powered wheelchairs. Journal of long-term effects of
medical implants, 14(2):107.
Elfes, A. (1989). Using occupancy grids for mobile robot
perception and navigation. Computer, 22(6):46–57.
Goldstein, H. (1980). Classical mechanics. Addison-
Wesley.
Gonzalez, R. and Woods, R. (2002). Digital image process-
ing. Prentice Hall.
Guo, S., Cooper, R., Boninger, M., Kwarciak, A., and Am-
mer, B. (2002). Development of power wheelchair
chin-operated force-sensing joystick. In [Engineering
in Medicine and Biology, 2002. 24th Annual Confer-
ence and the Annual Fall Meeting of the Biomedical
Engineering Society] EMBS/BMES Conference, 2002.
Proceedings of the Second Joint, volume 3, pages
2373–2374. IEEE.
Hershey, J. and Olsen, P. (2007). Approximating the
kullback leibler divergence between gaussian mixture
models. In Acoustics, Speech and Signal Processing,
2007. ICASSP 2007. IEEE International Conference
on, volume 4, pages IV–317–IV–320.
Huo, X. and Ghovanloo, M. (2010). Evaluation of a wire-
less wearable tongue-computer interface by individ-
uals with high-level spinal cord injuries. Journal of
Neural Engineering, 7(2).
Khalil, H. and Grizzle, J. (2002). Nonlinear systems, vol-
ume 3. Prentice hall New Jersey.
Lai, L., Wu, C., and Shiue, Y. (2007). A potential field
method for robot motion planning in unknown envi-
ronments. JOURNAL-CHINESE INSTITUTE OF EN-
GINEERS, 30(3):369.
Lund, M. E., Christensen, H. V., Caltenco Arciniega, H. A.,
Lontis, E. R., Bentsen, B., and Andreasen Struijk, L.
N. S. (2010). Inductive tongue control of powered
wheelchairs. In Proceedings of the 32nd Annual In-
ternational Conference of the IEEE Engineering in
Medicine and Biology Society, pages 3361–3364.
Mathews, J. (1992). Numerical methods for mathematics,
science, and engineering. Prentice Hall.
Mitra, A. (2008). Finite Difference Method for the Solu-
tion of Laplace Equation. Department of Aerospace
Engineering, Iowa State University.
Nijmeijer, H. and Van der Schaft, A. (1990). Nonlinear
dynamical control systems. Springer.
Rebsamen, B., Burdet, E., Guan, C., Zhang, I, H., Teo,
C. L., Zeng, Q., Laugier, C., and Ang, Jr., M. H.
(2007). Controlling a wheelchair indoors using
thought. IEEE INTELLIGENT SYSTEMS, 22(2):18–
24.
Sarkar, N. et al. (1994). Control of mechanical systems
with rolling constraints. The International Journal of
Robotics Research, 13(1):55.
Thrun, S. (2002). Probabilistic robotics. Communications
of the ACM, 45(3):52–57.
Tonin, L., Leeb, R., Tavella, M., and Perdikis, S. (2010).
The role of shared-control in BCI-based telepres-
ence. In Systems Man and Cybernetics (SMC), 2010
IEEE International Conference on, pages 1462–1466.
IEEE.
Vlassis, N., Sgouros, N., Efthivoulidis, G., Papakonstanti-
nou, G., and Tsanakas, P. (1996). Global path plan-
ning for autonomous qualitative navigation. In ictai,
page 354. Published by the IEEE Computer Society.
Yun, X., Kumar, V., Sarkar, N., and Paljug, E. (1992).
Control of multiple arms with rolling constraints. In
Robotics and Automation, 1992. Proceedings., 1992
IEEE International Conference on, pages 2193–2198.
IEEE.
AutonomousWheelchairforPatientswithSevereMotorDisabilities
101