
DAG – Index
A Compressed Index for XML Keyword Search
Stefan Böttcher, Marc Brandenburg and Rita Hartel
University of Paderborn, Computer Science, Fürstenallee 11, D-33102 Paderborn, Germany
Keywords: Keyword Search, XML, XML Compression, DAG.
Abstract: With the Growing Size of Publicly Available XML Document Collections, Fast Keyword Search Becomes
Increasingly Important. We Present DAG-Index, a New Indexing and Keyword Search Technique That Is
Suitable for DAG-Compressed Data and Has the Advantage That Common Sub-Trees Have to Be Searched
Only Once.
1 INTRODUCTION
Motivation: Nowadays, an increasing amount of
data in the web is available in form of XML docu-
ments. While query languages for XML data are
powerful search tools for expert users, the non-ex-
pert users who just want to retrieve information
related to some given keywords do not have the
technical knowledge to write these search queries.
Therefore, for these users which are the great major-
ity of users, there exists a great demand for efficient
keyword search for XML data, where a user can
write its query as a list of keywords expressing his
search query – similar as the user is used to do this,
when he uses a search engine within the internet.
Contributions: Our paper presents DAG-Index,
an approach to efficient keyword search within
XML data that is based on a compressed keyword
index. Prior to building of the index, DAG-Index
transforms the document into a DAG (directed
acyclic graph) which removes redundant sub-trees
from the document. DAG-Index uses proxy nodes
for searching repetitive sub-trees only once, if all the
searched keywords are found in the sub-tree.
Goal of XML Keyword Search: Keyword
search is known to many users e.g. in form of an
internet search engine. The user provides a list of
keywords, and the search engine returns a list of
documents containing these keywords.
Similar to the idea of traditional keyword search
is the idea of keyword search for XML data. The
user provides a list of keywords and gets all minimal
sub-trees of the document that contain all keywords.
A sub-tree is minimal w.r.t. a set of keywords, if
it contains all keywords, but does not contain a
smaller sub-tree that also contains all keywords.
This Paper’s Example: The example used in
this paper is a fragment of an XML document of a
university database. Our example contains infor-
mation about a student named “Alice” with ID
“1234” and a lecture with name “Arts” of which
“Alice” is a participant.
Fig. 1 shows the binary XML tree of this docu-
ment. The numbers in parentheses represent the
preorder number of each node.
A user might ask for all minimal sub-trees
containing the keywords (“name”, “1234”) in order
to retrieve the name of the student with id “1234".
The document contains several combinations of
nodes with labels “name” and “1234”, namely (4,7),
Figure 1: University Example as binary XML tree.
137
Böttcher S., Brandenburg M. and Hartel R..
DAG – Index - A Compressed Index for XML Keyword Search.
DOI: 10.5220/0004364101370140
In Proceedings of the 9th International Conference on Web Information Systems and Technologies (WEBIST-2013), pages 137-140
ISBN: 978-989-8565-54-9
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)
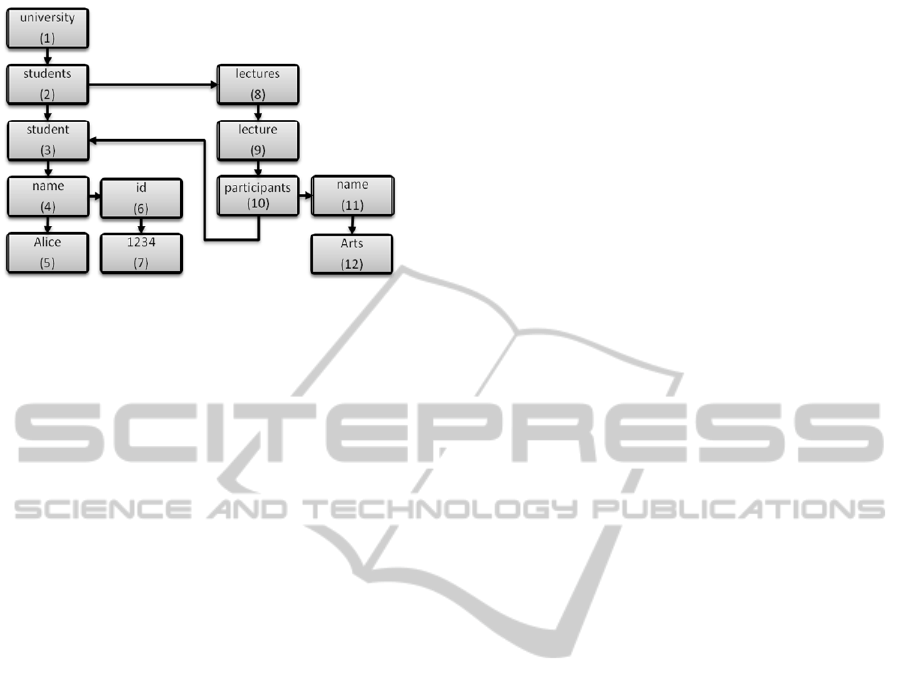
Figure 2: DAG of the example shown in Figure 1.
(4,15), (12,7), (12,15), (16,7), and (16,15). But
intuitively, only the combinations (4,7) and (12,15)
returning the sub-trees with roots 3 and 11 are
results expected by the user. Therefore, besides the
requirement to each result sub-tree that it must
contain all keywords, an additional requirement is
that a minimal result sub-tree must not contain
another result sub-tree. This property is called the
“shortest lowest common ancestor (SLCA)”. As e.g.
the combination (16,15) with root node 10 contains
the result with root 12, the result 10 is not consid-
ered as a solution.
2 XML KEYWORD SEARCH
ON AN UNCOMPRESSED
INDEX
Our paper follows the idea of anchor-based keyword
search as presented in (Sun, Chan, & Goenka, 2007).
The approach is based on inverted lists that store
for each keyword a list of references to the
document nodes with the keyword as node label.
Step 1: Chose an Anchor. Initially chose that
node n as an anchor that occurs last in document
order from all the first nodes of the inverted element
lists L
i
of the keyword w
i
.
If we consider a keyword search for w
1
=“name”
and w
2
=“1234”, we get the following two inverted
element lists: L
1
= (4,12,16) and L
2
= (7,15). There-
fore, we chose the node n=7 with label “1234” as
initial anchor.
Step 2: Compute the SLCA Candidates. Let L
n
be the inverted element list containing the anchor n.
We compute an SLCA candidate for a list M contai-
ning all nodes v
i
of each list L
i
that are closest to n.
For this purpose, in each inverted element list L
i
≠ L
n
of keyword w
i
, we chose first that v
i
that is the
last node in L
i
that precedes n as current node. The
node n and all these nodes v
i
form the initial list M
containing the match being currently regarded.
Considering our example, M = { 4,7 } .
Next, we repetitively check, whether the first
node v
i
of the list M belonging also to the list L
i
could be replaced by a node v
i
’ of L
i
following n in
document order and being closer to n. As long as we
find such a node v
i
’, we substitute v
i
by v
i
’, until no
replacement is possible anymore.
If we have checked for all nodes of the list M
whether or not they could be replaced by a node
closer to the anchor, the lowest common ancestor of
the set M is a result candidate. A node v1 is a lowest
common ancestor of M, lca(M), if v1 is a common
ancestor of all nodes in S and there is no common
ancestor v2V of S with v1 isanancestorofv2.
In our example, we check whether v
i
=4 could be
replaced by the node v
i
’=12. As 12 is not closer to 7
as 4, we do not replace 4 by 12. 4, the lca({4,7})
becomes a result candidate.
Furthermore, whenever replacing a node v
i
by
v
i
’, we have to chose v
i
’ as the next anchor if the
following holds: For each keyword w
j
(i≠j), there
exists a node that occurs after the old anchor n and
before v
i
’ in document order.
Whenever we have computed a result candidate,
we form a new set M’ that contains for each inverted
element list L
i
the node v
i
’ following v
i
€ M in L
i
.
We chose the element of M’ that comes last in
document order as new anchor and proceed with
Step 2, until we have reached the end of the
document.
Step 3: Compute the Result set from the Set C
of candidates. Finally, we remove all nodes ca C
from the set of candidates C for which a node cdC
exists such that ca is an ancestor of cd. All
remaining nodes form the result set R.
In our example, the final result set consists of the
nodes 4 and 12.
3 XML KEYWORD SEARCH
BASED ON A DAG-INDEX
While redundancies are avoided in relational
databases, they are nearly unavoidable for XML data
and occur, e.g., if the data modelled contains many-
to-many relationships. Such redundancies are
typically removed by DAG compression, where a
repetitive occurrence of a sub-tree is replaced by a
pointer to the first occurrence. Fig. 2 shows the
DAG of the example document shown in Fig. 1.
Instead of computing the inverted elements lists
WEBIST2013-9thInternationalConferenceonWebInformationSystemsandTechnologies
138

L
i
for each keyword k
i
based on the XML document,
we compute the keyword list based on the com-
pressed DAG of the XML document. Besides
keeping the index small, our goal of using DAG
compression is to search shared sub-trees only once
and thereby to achieve a faster search speed.
3.1 Compressed Index
Prior to computing the index, we transform the XML
document into its minimal DAG by replacing each
repeated occurrence of a sub-tree with a pointer to
the sub-tree’s first occurrence.
Similarly as for the uncompressed index, our
compressed index consists of inverted element lists
L
i
for each potential keyword k
i
that occurs as an
element label or as a text node within the DAG. We
do a bottom-up search for DAG nodes with multiple
incoming edges and split the DAG into multiple sub-
DAGs as follows: Whenever a node v of the DAG D
has more than one incoming edge, i.e., v has the
incoming edges ev
1
, …, ev
n
, we remove v from D
and start a new sub-DAG Dv, where Dv is a copy of
D with all nodes not being a descendant-or-self of v
in D being removed from Dv and with all dangling
edges being removed, such that v is the root node of
Dv. Let Lv be the set of labels occurring in Dv. Each
edge ev
j
gets a new (virtual) target node p
j
, called
proxy node of v, and for each k
i
Lv, p
j
is added to
the inverted element list L
i
representing all the oc-
currences of keyword k
i
in D.
Additionally, the information that v
j
is a proxy
node for v is stored in a table of proxy references
where each node v
j
has a reference to the root node v
of Dv.
Fig. 3 shows the document of our example where
the DAG is split into two DAGs connected by the
proxy nodes p1 and p2 (represented by white
rectangles) and their references to the second DAG’s
root node (1’).
3.2 Keyword Search on the compressed
Index
Keyword search on the compressed index works
similar to keyword search on the uncompressed
index, with the following differences: Due to the
introduction of proxy nodes that represent multiple
keywords occurring in a sub-DAG, the same proxy
node-ID may occur in multiple inverted element
lists, and the same proxy node-ID may occur
multiple times within the currently considered list M
of actual nodes. Whenever during the computation
of M, all elements of M contain the same proxy node
Figure 3: Document showing 2 DAGs and proxy nodes.
v
j
, where v
j
refers to the root node v of a sub-DAG
Dv, the complete match is contained in Dv or in a
sub-DAG of Dv. In this case, first, we remove a
possible SLCA candidate C in D, second, if C ≤
a
v
j
,
we perform the keyword search in Dv, and third, we
start a new keyword search within D with a new
anchor among the nodes after v
j
, i.e., we continue
after we have increased the pointer positions in all
inverted keyword lists of D to next(v
j
). In this case,
we have the advantage of computing the SLCAs
within Dv only once for all shared sub-trees repre-
sented by Dv. Whenever this optimization is possi-
ble, we yield a faster search compared to computing
all these solutions individually.
In the example of Fig. 3, the first anchor node is
the proxy node p1 and v
i
is the same proxy node p1.
As all nodes in M represent the same proxy node p1,
we recursively start a new search at the node (1’)
referred to by p1, i.e., inside the second DAG.
Within this DAG, we find that the node with
preorder position (2’) is a SLCA. Later, the second
anchor node found in first DAG is the proxy node p2
and a corresponding node v
i
is the same proxy node
p2. As p2 also refers to node (1’) which now has
already been investigated, no new search starting in
(1’) is required. Thereby, we have dynamic
programming to compute the SLCAs for both shared
sub-trees in parallel – whereas, within the non-
compressed XML tree index, we had to compute the
results in both sub-trees sequentially.
4 RELATED WORKS
There exist several approaches that address the
problem of keyword search in XML. On the one
hand, there are approaches that examine the
semantics of the queries to achieve query results of
higher relevance (Guo et al., 2003), (Petkova et al.,
2009), and (Li et al., 2010).
DAG-Index-ACompressedIndexforXMLKeywordSearch
139

On the other hand, there are approaches that con-
centrate on a higher performance for the computa-
tion of the set of query results.
Early approaches were computing the LCA for a
set of given keywords on the fly (Schmidt et al.,
2001). Recent approaches try to enhance the query
performance by using a pre-computed index. The
approach (Florescu et al., 2000) is based on storing
the inverted element lists within a relational
database.
(Li et al., 2004) present an approach based on
computing the MLCA with the help of XQuery
operations and a second approach that, similar as
XKSearch (Xu and Papakonstantinou, 2005),
processes the document bottom-up in order to
compute the index and store all nodes not yet com-
pletely parsed on a stack. Whenever a node is found
as result, all its ancestors are removed from the
stack, as they cannot form a result anymore.
JDeweyJoin (Chen and Papakonstantinou, 2010)
returns the top-k most relevant results. They com-
pute the results bottom-up based on a kind of join on
the lists of DeweyIDs of the nodes in the inverted
element lists. They sort the list entries according to a
weight function and stop the computation after k
results, returning the top-k most relevant results.
(Zhou et al., 2012) present an approach that en-
riches the inverted element lists by all ancestor-
nodes of the nodes with the keyword as label. There-
fore, they can compute the SLCAs by intersecting
the inverted element lists with the list of keywords
and by finally removing each result candidate, the
descendant of which is another result candidate.
Our paper focuses on efficient result computa-
tion. It follows the anchor-based approach as it was
presented in (Sun et al., 2007). However, different
from all other contributions, instead of computing an
XML-index, we compute a DAG-Index. This
enables us to compute several keyword search
results in parallel, and thereby speeds-up the SLCA
computation. To the best of our knowledge, DAG-
Index is the first approach that improves keyword
search by using XML compression before comput-
ing the search index.
5 SUMMARY
AND CONCLUSIONS
Keyword search is of increasing interest for search-
ing relevant data within large XML document col-
lections, especially for the huge majority of non-
expert users. Due to the increasing amount of pub-
licly available data in the XML format, there is an
increasing interest in fast keyword search tech-
niques. We have presented DAG-Index, an indexing
and keyword search strategy for large XML docu-
ments that allows compressing an XML tree and the
search index in such a way that common sub-trees
have to be indexed only once. As a consequence, a
repeated keyword search within a repeated sub-tree
can be avoided. We consider our DAG-Index-based
keyword search to be a significant contribution to
improve the search performance especially for the
majority of the non-expert users.
REFERENCES
Chen, L. J., & Papakonstantinou, Y. (2010). Supporting
top-K keyword search in XML databases. Proceedings
of the 26th International Conference on Data
Engineering. Long Beach, CA, USA.
Florescu, D., Kossmann, D., & Manolescu, I. (2000).
Integrating keyword search into XML query
processing. Computer Networks , 33.
Guo, L., Shao, F., Botev, C., & Shanmugasundaram, J.
(2003). XRANK: Ranked Keyword Search over XML
Documents. Proceedings of the 2003 ACM SIGMOD
International Conference on Management of Data.
San Diego, California, USA.
Li, J., Liu, C., Zhou, R., & Wang, W. (2010). Suggestion
of promising result types for XML keyword search.
13th International Conference on Extending Database
Technology. Lausanne, Switzerland.
Li, Y., Yu, C., & Jagadish, H. V. (2004). Schema-Free
XQuery. (e)Proceedings of the Thirtieth International
Conference on Very Large Data Bases. Toronto,
Canada.
Petkova, D., Croft, W. B., & Diao, Y. (2009). Refining
Keyword Queries for XML Retrieval by Combining
Content and Structure. Advances in Information
Retrieval, 31th European Conference on IR Research.
Toulouse, France.
Schmidt, A., Kersten, M. L., & Windhouwer, M. (2001).
Querying XML Documents Made Easy: Nearest
Concept Queries. Proceedings of the 17th
International Conference on Data Engineering.
Heidelberg, Germany.
Sun, C., Chan, C. Y., & Goenka, A. K. (2007). Multiway
SLCA-based keyword search in XML data.
Proceedings of the 16th International Conference on
World Wide Web. Banff, Alberta, Canada.
Xu, Y., & Papakonstantinou, Y. (2005). Efficient
Keyword Search for Smallest LCAs in XML
Databases. Proceedings of the ACM SIGMOD
International Conference on Management of Data.
Baltimore, Maryland, USA.
Zhou, J., Bao, Z., Wang, W., Ling, T. W., Chen, Z., Lin,
X., et al. (2012). Fast SLCA and ELCA Computation
for XML Keyword Queries Based on Set Intersection.
IEEE 28th International Conference on Data
Engineering. Washington, DC, USA.
WEBIST2013-9thInternationalConferenceonWebInformationSystemsandTechnologies
140
