Schema-based Parallel Compression and Decompression

of XML Data

Stefan Böttcher, Matthias Feldotto and Rita Hartel

University of Paderborn, Computer Science, Fürstenallee 11, D-33102 Paderborn, Germany

Keywords: XML, XML Compression, Parallelization.

Abstract: Whenever huge amounts of XML data have to be transferred from a web server to multiple clients, the

transferred data volumes can be reduced significantly by sending compressed XML instead of plain XML.

Whenever applications require querying a compressed XML format and XML compression or

decompression time is a bottleneck, parallel XML compression and parallel decompression may be of

significant advantage. We choose the XML compressor XSDS as starting point for our new approach to

parallel compression and parallel decompression of XML documents for the following reasons. First, XSDS

generally reaches stronger compression ratios than other compressors like gzip, bzip2, and XMill. Second,

in contrast to these compressors, XSDS not only supports XPath queries on compressed XML data, but also

XPath queries can be evaluated on XSDS compressed data even faster than on uncompressed XML. We

propose a String-search-based parsing approach to parallelize XML compression with XSDS, and we show

that we can speed-up the compression of XML documents by a factor of 1.4 and that we can speed-up the

decompression time even by a factor of up to 7 on a quad-core processor.

1 INTRODUCTION

1.1 Motivation

XML has become a de facto standard data exchange

format in the web, although, due to the verboseness

of XML data, transfer time may become a serious

bottleneck in web applications. Whenever huge

amounts of XML data have to be transferred from a

web server to multiple clients, and client

applications have to evaluate queries locally on the

transferred XML data, then transferring XML data

in a compressed, but queriable data format, instead

of transferring plain XML data, may become an

interesting solution for preventing the bottleneck.

Within such an architecture, XML data is

compressed on the server’s side, and compressed

XML data is submitted to multiple clients, which not

only reduces the transmitted data volume, but also

significantly increases the transmission speed. On

the clients’ side, the data can be further processed in

compressed format, e.g., whenever query evaluation

on the compressed XML format is faster than on

uncompressed XML, or it can be decompressed,

e.g., whenever uncompressed XML has to be

processed further. However, when large XML data

fragments are processed, compression time on a

server, and even worse, decompression time for

client applications may become a bottleneck.

While generic compressors like gzip or bzip2 or

early XML specific compressors like XMill allow

for a reasonable compression ratio and a fast

compression and decompression, they do not support

query processing on the compressed data, i.e., they

require a prior decompression in order to query the

compressed data. On the other hand, there exist

XML compressors like XML Schema Subtraction

(XSDS) (Böttcher et al., 2010) that not only provide

stronger compression ratios than these generic data

compressors and than XMill (Liefke and Suciu,

2000), but also allow for query evaluation and direct

search on the compressed data at a speed that is

faster than that of XPath query evaluation on the

original uncompressed XML data (Böttcher et al.,

2012).

The greatest deficiency of XSDS currently is the

time needed to compress and to decompress the data.

To overcome the lack of compression and

decompression speed, we provide an approach for

parallelizing both, the XSDS compression and the

decompression which leads to significant speed-up

for client devices containing a multi-core processor.

Böttcher S., Feldotto M. and Hartel R..

Schema-based Parallel Compression and Decompression of XML Data.

DOI: 10.5220/0004366300770086

In Proceedings of the 9th International Conference on Web Information Systems and Technologies (WEBIST-2013), pages 77-86

ISBN: 978-989-8565-54-9

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

1.2 Contributions

In this paper, we present an approach to speed up the

schema-based XML document compression and

decompression of XSDS, which to the best of our

knowledge is the only approach that combines the

following properties:

 It supports a self-organized parallelization, i.e.

parallel compression and decompression can be

achieved on arbitrary large XML documents that are

not yet fragmented into handy parts.

 As a key contribution it contains an automated

separation of input XML documents into fragments

that can be compressed independently of each other.

 This includes an approach that analyzes a given

XML schema or DTD and that determines text

positions within the input XML document which are

suitable for a good separation of the XML document

into fragments that can be compressed

independently.

 Furthermore, the approach uses a String-based fast

XML parser that does not require the XML

document to be tokenized into e.g. SAX events, i.e.

a parser that very efficiently separates the XML

document into several smaller, independent data

fragments.

 Finally, compressed data is enriched to support

efficient parallel decompression.

Additionally, we present the performance

improvements by parallel XSDS compression and

parallel XSDS decompression. This includes a

speed-up factor of 7 for the decompression that we

have achieved on a quad-core processor.

1.3 Paper Organization

This paper is organized as follows: Section 2

summarizes the basic idea of XSDS followed by a

description of how XSDS is being used for

compressing XML data. Section 3 describes the

fundamental concepts used by our approach to

parallelize the compression and the decompression

of the XML data via XSDS. The fourth section

outlines some of the experiments that compare our

prototype with other XPath evaluators. Section 5

gives an overview of related work and is followed

by the Summary and Conclusions.

2 A SUMMARY OF XSDS

AND THE PAPER’S EXAMPLE

2.1 The Basic Idea of XSDS

Compression

The main compression principle of XML schema

subtraction (XSDS) is to remove all the information

that is strictly defined by a DTD or an XML schema

definition from a given XML document, and to

encode only those parts of the XML document in the

compressed format that can vary according to the

DTD or XML schema. In this paper, we only

provide a short overview of XSDS compression, as

details are described in (Böttcher et al., 2010).

2.2 This Paper’s Example

To illustrate the ideas of our approach, we use an

example of a schema that represents a university.

Each document consists of a <university> element

that contains a sequence of one <courses> element

followed by one <staff> element. The <courses> ele-

ment consists of any number of <course> elements.

The <staff> element contains any number of

elements which are either <professor> or <assistant>

elements. The elements <course>, <professor>, and

<assistant> contain PCDATA only.

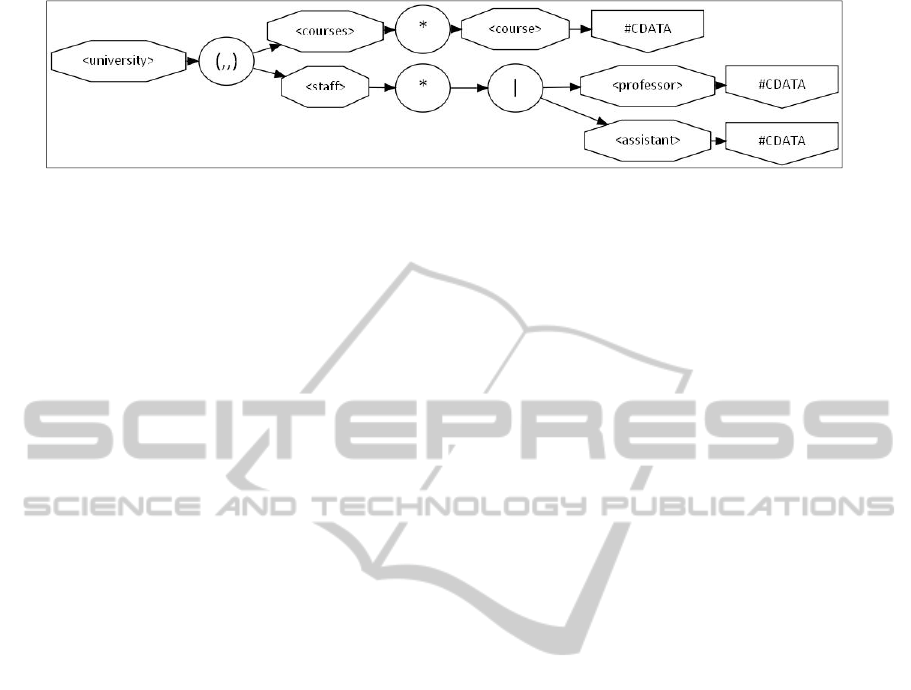
Fig. 1 shows a visualization of our example

schema S, called the rule graph of S. The node with

label ‘(,,)’ is called a sequence node that defines a

sequence of all its child nodes in the given order. It

corresponds to an <xsd:sequence> element within an

XML schema and to a comma-operator within a

DTD rule. The node with label ‘*’ is called a

repetition node that defines any number of

occurrences of its child node. It corresponds to non-

default values of the attributes minOccurs and

Figure 1: Rule graph of our example schema.

WEBIST2013-9thInternationalConferenceonWebInformationSystemsandTechnologies

maxOccurs within an XML schema and to a ‘*’-

operator within a DTD rule. The node with label ‘|-is

called a choice node that defines the choice among

its child nodes. It corresponds to the <xsd:choice>

element within an XML schema and to a ‘|’-operator

within a DTD rule.

Fig. 2 shows an example document that conforms

to the given rule graph and that consists of 3 courses,

2 professors, and 1 assistant.

2.3 Compressing the Example

Document

Compressing the Structure. Within the structure of

an XML document, i.e., within the element tags,

there are only three different concepts that allow for

variant parts within an XML document defined by a

given schema: First, when the schema requires the

choice of one out of different given alternatives.

Second, when the XSD element ‘all’ requires the

occurrence of all elements declared by children of

the ‘all’ element, but they can occur in any order.

Third, when the XSD requires a repetition of an

element, but leaves it open how often this element

occurs. For DTD, we have to consider ‘|’ and ‘*’.

The compression of these variant parts within an

XML document works as follows. Each compression

step assumes that we consider one current position

in the XML document at a time for which the XSD

allows variant parts. For each current position in the

XML document for which the XSD allows a choice,

we only store the alternative chosen at this current

position (This requires log(n) bits, if there are n

possible alternatives.) For each XSD element ‘all’,

we only encode the order of the elements required

by the children of the ‘all’ element in the XSD. (This

requires

∑

log





bits, if there are n possible

alternatives.) Finally, for each repetition of elements

starting at a given position within an XML

document, we only store the number of occurrences

of this element found at the current position of the

XML document. (

If the number of children per node is

e.g. limited by 2^32 (MAXINT), this requires 1 to 5 bytes

per repetition node, depending on the concrete number of

repetitions.

)

For example, for the schema given in Fig. 1 and

the document given in Fig. 2, we have to encode a 3

to represent the number of courses, followed by a 3

to determine the number of staff members followed

by a 0-bit representing the chosen alternative (first

staff member is a professor), followed by a 1-bit

(second staff member is an assistant), and finally

followed by the 0-bit (third staff member is a

professor). Thus, the whole structure of the example

document given in Fig. 2 can be represented by 2

integer numbers plus 3 bits.

Compressing the Textual Data. Beneath the

structure, an XML document contains textual data.

We store the text data in document order in a text

container and apply gzip on top of the text container

at the end of the document.

Decompression. The rule graph is also used for

the reverse process, i.e., decompressing the

compressed XML structure and the compressed text

container back to the original XML document (as

described in (Böttcher, Hartel & Messinger, 2010)).

3 PARALLEL COMPRESSION

3.1 Basic Idea of the Parallelization

The parallel compression of XML data is performed

in 3 steps. The first step is a preprocessing step that

has to be performed only once per schema (XSD or

DTD). In this step, we analyze only the schema to

determine which text positions are promising

candidates to separate the XML document into

several fragments. In the second step, we perform

the real fragmentation of the XML document.

Finally, in the third step, we compress each fragment

independently and in parallel by using XSDS.

Furthermore, we augment the compressed data to

packages containing the compressed data fragments

plus additional meta-data containing the start and

end addresses of the fragments within the

compressed data, such that the parallel

decompression can be performed efficiently.

Then parallel decompression can be performed in

2 steps as follows. In the first step, the compressed

data packages are separated back into fragments. In

the second step, the fragments are decompressed in

parallel by XSDS. As this does require nearly no

additional work, the overhead by the parallelization

is minimal for the decompression, such that we can

</courses>

<staff>

<assistant>Peter</assistant>

</staff>

</university>

Figure 2: An example XML document.

Schema-basedParallelCompressionandDecompressionofXMLData

expect a high speed-up within the decompression

phase. This is of particular interest when

decompression is used much more frequently than

compression, for example when compressed data is

downloaded and decompressed multiple times.

3.2 Step 1: Determining Promising

Fragmentation Candidates

In the first compression step, we analyze only the

rule graph of the schema, and we do not need any

access to any XML document. Therefore, this step

can be performed as a preprocessing step and does

not have to be repeated for different XML input

documents.

The goal of this step is to determine promising

candidates in the rule graph, at which the input

document could be fragmented into several

document fragments. For promising candidates

within the rule graph, we have two different criteria:

a structural criterion on the one hand, and a criterion

conforming to the depth and the expected size of the

fragments on the other hand.

The idea behind the structural criterion is that

those rule graph nodes are promising candidates that

have child nodes in the rule graph which correspond

to a lot of document nodes within the XML

document, as then, the document can be split at each

of these document nodes. If we look at the rule

graph, we can see that three kinds of rule graph

nodes fulfill this condition: the sequence nodes, the

repetition nodes, and the ALL nodes, each of which

may have several child nodes within the XML

document. In contrast, for each visit of a choice node

while processing the rule graph, there is only one

XML document node processed, if the child node of

the choice node in the rule graph is an element node.

Therefore, we consider each sequence node, each

repetition node, and each ALL node within the rule

graph as a promising candidate for fragmenting the

XML input document.

As splitting an XML document into too many

fragments may cause unnecessary overhead, we

introduce a depth threshold that avoids selecting

candidates that might lead to a too small document

fragment as a second criterion.

The first step therefore involves a preorder walk

through the rule graph which selects each sequence

node, each repetition node, and each ALL node that

lies above the specified depth threshold as a

promising fragmentation candidate. This set of

candidate nodes is then the input for the next step,

the fragmentation of the input document.

3.3 Step 2: Fragmenting the Input

Document

To fragment a given XML document, we have to

find matchings of the candidates that were identified

in Step 1. As the parallelized compression shall be

faster than a sequential compression, the

fragmentation has to be very fast. How much faster

the parallel processing is, in contrast to the

sequential processing, depends mainly on how fast

the fragmentation of the XML document into several

fragments is. Therefore, we do not use an approach

that requires the XML input document in form of

SAX events or other tokenized data. Instead, we

work on the String representation of the XML

document itself in order to find the elements that

correspond to the candidates selected in Step 1.

The key idea is to reduce the search for these

XML elements to a search for multiple substrings.

For this purpose, we use a String-based XML filter

approach presented in (Böttcher et al., 2012).

For the example schema given in Fig. 1, the

candidates are the sequence node and the two

repetition nodes, i.e., we have to search for positions

of the elements <courses>, <course>, <staff>,

<professor>, and <assistant>. At the same time, we

know the structure of the document, i.e., the nesting

of the elements, given by the schema. This means, at

the beginning, we search within a fast String search

for occurrences of ‘<courses’. As soon as we have

found a position of an element <courses>, we search

instead for ‘<course’ or ‘</courses’, as either

‘<course’ indicates that an additional <course>

element is found or ‘</courses’ indicates that no

more <course> element is found as a child of the

current <courses> element. Similar, when we have

found a position of an element <staff>, we search for

‘<professor’, ‘<assistant’, or ‘</staff’. For details on

this String-based XML filtering algorithm, please

refer to (Böttcher et al., 2012).

This String-based XML filtering allows for a fast

search for text positions in the XML document

corresponding to the candidates determined in Step

1. While this approach parses the String

representation, it counts the number of characters

read. As soon as a minimum size threshold for a

document fragment is exceeded by an XML element

tag, a new fragment is started and the old fragment

together with the fragment’s location information is

passed to one of the processes performing Step 3.

The fragment’s location information contains the

following components: first, a rule graph path PR

that corresponds to the path PF from the document

root to the root of the fragment, second, for each

WEBIST2013-9thInternationalConferenceonWebInformationSystemsandTechnologies

repetition node in PR, the number of repetitions

found in the XML document that precede PF.

3.4 Step 3: Parallel Compression

The parallel compression is similar to the sequential

compression of standard XSDS. The important

difference however is, that the compression does not

start at the root node of the rule graph, but at that

rule graph node given by a path PR from the root

node to the specified rule graph node that was

passed to the compression process by Step 2.

Starting at that rule graph node determined by

PR, the compression process traverses the rule graph

in preorder. Whenever compression passes an

element node, it consumes an element within the

document fragment. Whenever compression passes a

#PCDATA node, it consumes a text node within the

document fragment and stores it in the

corresponding text container. Whenever

compression passes a choice node, it determines the

chosen alternative and encodes it in the compressed

data. Whenever compression passes a repetition

node, it increases a counter for each occurrence

within the document that is written into the

compressed data. And finally, whenever

compression passes a sequence node, it proceeds

with the children of this sequence node.

Whenever a fragment is compressed completely,

the compressed data is written to the output

document or is transferred to a receiver.

In order to restore the decompressed document in

the right order at the receiver’s side, the fragment’s

location information is being used, such that the

decompressor can restore the original order.

3.5 Modified Data Format

In order to be able to decompress the compressed

document fragments in parallel, i.e., independently

of each other and in any order, the compressed data

has to be enriched by additional meta-data.

Therefore, the output of the compressor is a package

that contains one compressed data fragment plus a

header specifying the path PR within the rule graph

from the root node to that rule graph node where to

start the decompression. Furthermore, for each

repetition node for an element or a fragment E on

this path, we store the number of occurrences of E

that are stored in this document fragment.

Besides this meta-data, each package contains a

unique number which defines the order in which the

decompressed data has to be concatenated and the

size of the compressed document packages in bytes.

The complete compressed data then consists of

the concatenation of all compressed document

packages including the meta-data.

3.6 Parallel Decompression

The parallel decompression is similar to the

sequential decompression, except for the

fragmentation of the compressed data and for

determining each fragment’s corresponding rule

graph node, which is needed for decompression.

The fragmentation process utilizes the size

information contained in the meta-data of each

package in order to split this package from the

remaining packages. Each package are then passed

to an own decompression process running in parallel

to all the other decompression processes.

Each decompression process uses the meta-data

for calculating the fragment’s corresponding start

node within the rule graph. Similar to each

compression process, each decompression process

traverses the rule graph in preorder. Whenever

decompression passes an element node within the

rule graph, it writes the corresponding element to the

decompressed data. Whenever decompression passes

a #PCDATA node, it reads a text value from the

corresponding text container and writes it to the

decompressed data. Whenever decompression passes

a choice node, it reads the chosen alternative from

the compressed data and it proceeds with

decompressing the chosen alternative. Whenever

decompression passes a repetition node, it checks

from the compressed data whether or not a further

occurrence follows and continues with

decompressing the further occurrence or the next

node in preorder. And finally, whenever

decompression passes a sequence node, it proceeds

with the children of this sequence node.

4 EVALUATION

OF OUR PROTOTYPE

IMPLEMENTATION

4.1 Evaluation Environment

For our performance evaluation, we used a quad-

core system, Intel Core 2 Quad Q8200 2,33GHz,

with 2x DDR2 RAM 800MHz, 2048MB memory

and with a 7200rpm 500GB SATA hard disk.

To evaluate the presented compression approach

and to compare it with other approaches, we have

used two different XML benchmarks: XMark

Schema-basedParallelCompressionandDecompressionofXMLData

0,05

0,1

0,15

0,2

0,25

0,3

0,35

catalog-01 catalog-02 dictionary-01 dictionary-02 XMark01 XMark1 XMark3

compression ratio

gzip bzip2 XMill Succinct RePAIR XSDS XSDS [p]

(Schmidt et al., 2002) and XBench (Yao et al.,

2004).

In order to get representative evaluation results,

we have used the two benchmarks for generating

documents of different types, different sizes, and

with different structure quota as listed in Table 1.

Table 1: Data used in our evaluation.

Abbr. Description size Structure

XMark01

XMark

benchmark with

factor 0.1

11.3

26.23 %

XMark1

XMark

benchmark with

factor 1

113.0

26.10 %

XMark3

XMark

benchmark with

factor 1

340.0

26.05 %

catalog-01

XBench data-

centric

benchmark

10.5

55.23 %

catalog-02

XBench data-

centric

benchmark

105.0

55.21 %

dictionary-

XBench text-

centric

benchmark

10.7

20.87 %

dictionary-

XBench text-

centric

benchmark

106.0

20.81 %

We have compared the presented approach with the

following alternatives, ranging from XML non-

aware, to encoding-based, to grammar-based, to

schema-based approaches to XML compression.

From each category one or two representatives are

chosen for the evaluation (c.f. Table 2).

Table 2: The evaluated approaches for XML compression.

Abbr. Description Type

gzip

default gzip

implementation

XML non-

aware

gzip [p]

parallel default

implementation

XML non-

aware

bzip2

default bzip2

implementation

XML non-

aware

bzip2 [p]

parallel bzip2

implementation

XML non-

aware

XMill

default XMill

implementation

encoding-

based

Succinct

default Succinct

implementation

encoding-

based

RePAIR

default RePAIR

implementation

grammar-

based

XSDS

starting point of this

paper

schema-

based

XSDS[p]

approach of this

paper

schema-

based

In addition to our parallel approach, we evaluate two

further parallel compressors (marked with [p]): gzip

[p] (Adler) and bzip2 [p] (Gilchrist). In contrast to

our approach, they only implement the concept of

gzip and bzip2 in a parallel way. In particular, they

only separate the input data into several packages of

equal sizes and compress these packages in parallel.

Then, the separately compressed packages will be

put together, which yields the default package

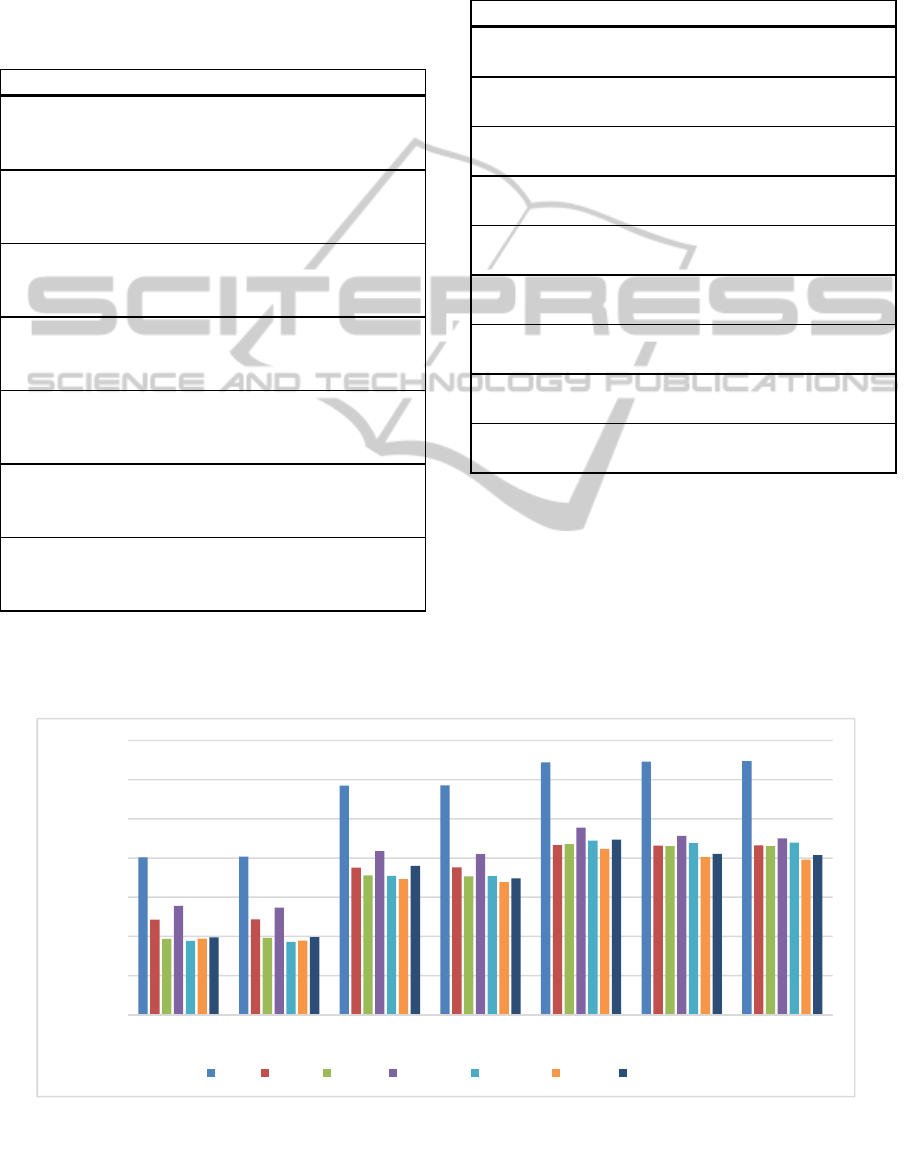
Figure 3: Compression ratios for different files.

WEBIST2013-9thInternationalConferenceonWebInformationSystemsandTechnologies

100

150

200

250

300

350

400

450

gzip gzip [p] bzip2 bzip2 [p] Xmill Succinct RePAIR XSDS XSDS [p]

Throughput (MBits/s)

compression decompression

0,05

0,1

0,15

0,2

0,25

0,3

gzip gzip [p] bzip2 bzip2 [p] Xmill Succinct RePAIR XSDS XSDS [p]

compression ratio

format of gzip/bzip2. Therefore, there is no

information about the separate packets saved in the

compressed data, and as a consequence, the

decompression cannot be parallelized as in our

approach.

In order to get stable results and to avoid random

variations, each evaluation run was started 10 times

with flushed memory and with the same parameters,

and the average of the 10 results was taken.

4.2 Evaluation Results

Figure 3 summarizes the results comparing the

compression ratio of the different compressors for

the sample benchmark files. XSDS has the best

compression ratio for all sample benchmark files

except for the catalog benchmark, a dataset with

high structure ratio, where RePAIR is a little bit

better, but the parallel XSDS achieves very good

results, too: Although the compressed file is a little

bit greater than in serial XSDS due to the meta-data

required, the parallel XSDS compressor has the

second best compression ratio for each sample

benchmark file except for the small sample files and

the catalog benchmark. Therefore, we expect

parallel XSDS to be a useful processor for

compressing large XML files.

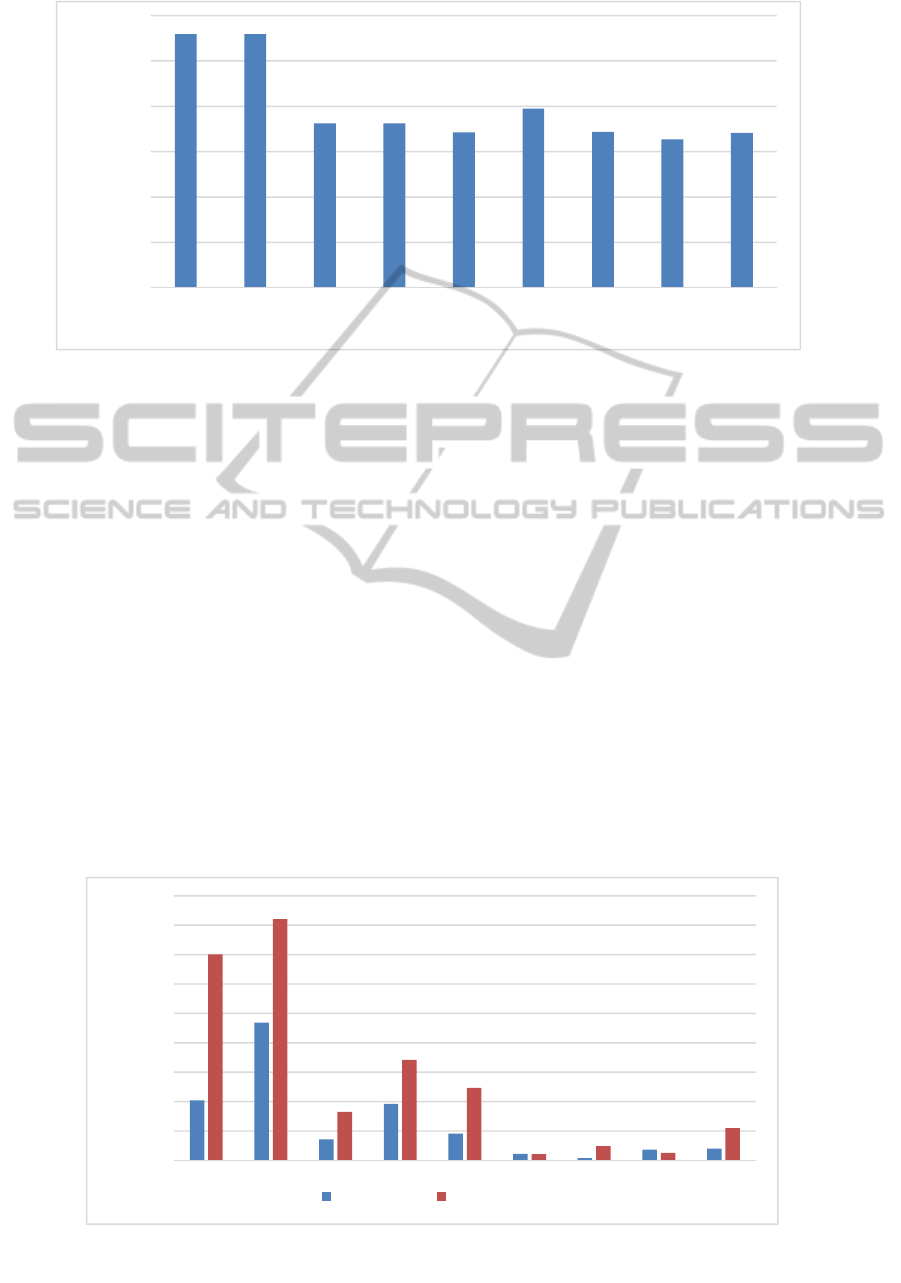
Figure 4 summarizes the results comparing the

average compression over all sample files. Also

here, in the summarized results, the new parallel

XSDS processor has the second best compression

ratio, shortly after the serial XSDS compressor, i.e.,

all other compared compressors have worse

compression ratios.

Figure 5 summarizes the results comparing the

compression and decompression speeds. The XML

non-aware compressors have higher compression

and decompression throughputs than all the XML

aware compressors. However, the new parallel

XSDS compressor is the fastest XML compressor,

Figure 4: Average compression ratio.

Figure 5: Average throughput rates for compression and decompression.

Schema-basedParallelCompressionandDecompressionofXMLData

which generates a compressed data format that is

also queriable. In particular, for the decompression,

which is the most interesting direction when

compressed files are downloaded and decompressed

multiple times, parallel XSDS is faster than

Succinct, RePAIR, and XSDS, and also the gap to

the compression speed of the XML non-aware

compressors is smaller.

Finally, we compare the possible speed-up

factors of the parallel compression variants

compared to their sequential pendants. The parallel

gzip compressor reaches average speed-up factors of

2.99 for compression and 1.17 for decompression of

XML data. The bzip2 compressor reaches average

speed-up factors of 2.7 for compression and 2.07 for

decompression of the XML data. However, our

parallel XSDS compressor reaches average speed-up

factors of 1.10 for compression and 4.29 for

decompression. For the largest file, i.e. catalog-02,

we even get a speed-up factor of 7.

The speed-up factor achieved by parallel XSDS

for compression is smaller than for decompression

for the following reason: During the compression,

the input files also have to be separated into

packages by using the StringFilter; this step is not

needed during decompression because the separation

is saved in the packets.

Especially when decompression of XML files is

executed more often than compression, e.g., when

multiple users download compressed XML files

from a web server, our approach to parallelize XSDS

gets the best speed-up factor by parallelization of all

the approaches to parallelize an XML compressor.

To summarize, as parallel XSDS it the fastest

compressor generating a queriable compressed data

format, and additionally achieves the best

compression strength on large XML files (except for

serial XSDS), we consider our parallel XSDS to be a

significant contribution to the field of providing

compressed data in web-based information systems.

5 RELATED WORKS

To the best of our knowledge, there do not exist

XML specific compressors that use parallelization to

speed up their compression or decompression.

In contrast to the XML specific compressors,

there exist generic compressors that can be applied

to any type of data. Typical representatives of this

family of compressors are gzip (based on LZ77 and

Huffman) or bzip2 (based on Burrows-Wheeler

Transform followed by Move-To-Front and

Huffman). In general, each XML file can be

regarded simply as a chain of bytes without any

connection between these bytes. Then the data could

be simply chopped into several chunks by random or

into chunks of fixed size and each chunk of data

could be compressed independently of the other

chunks in parallel by generic data compressors.

Following this idea, each generic data compression

approach could be parallelized. The greatest

disadvantage of this idea is that by ignoring

connections between the chunks, redundancies are

not detected, such that a loss of compression ratio is

the consequence. This idea is mainly followed by

pigz (Adler) and PBZIP2 (Gilchrist), which are the

parallel versions of gzip or bzip2 respectively. They

both compress chunks of data independently of the

other chunks and concatenate the output of the

processes to one compressed file following the

compressed file format of gzip or bzip2 respectively.

(Howard and Vitter, 1996) present ideas for the

parallelization of Huffman encoding or other prefix

codes like Golomb and Rice and for arithmetic

encoding for image data. The main idea is that each

processor compresses one pixel at a time. All

processors follow the same pulse and write one bit

of the calculated code to the output at one heart beat.

In order to decompress, each processor reads one bit

of the compressed code at one heart beat, and as

soon as the code is complete (which can be

determined because of the prefix property), the

processor can decode the code and – as soon as all

processors have finished the decoding – can write

the decoded information to the output.

Regarding XML structure compression, there

exist several approaches, which can be mainly

divided into three categories: encoding-based

compressors, grammar-based compressors, and

schema-based compressors.

The encoding-based compressors allow for a

faster compression speed than the other ones, as only

local data has to be considered in the compression as

opposed to considering different sub-trees as in

grammar-based compressors.

The XMill algorithm (Liefke and Suciu, 2000),

XGrind (Tolani and Haritsa, 2002), XPRESS (Min

et al., 2003), XQueC (Arion et al., 2007), and the

approach presented in (Bayardo et al., 2004) belong

to the first group. The latter four approaches allow

querying the compressed data. Furthermore, the

encoding-based compression approaches (Cheney,

2001), (Girardot and Sundaresan, 2000), and in

(Zhang et al., 2004) enrich the compressed data by

additional information that allows for a fast naviga-

tion.

We assume, that a trivial parallelization approach

WEBIST2013-9thInternationalConferenceonWebInformationSystemsandTechnologies

should be applicable to all encoding based

compression techniques: Simply chop the XML data

at any XML token (i.e., before a ‘<’ character or

after a ‘>’ character) and compress the chunks

independently of each other. As the encoding-based

compressors do not consider the structure of an

XML file, but simply compress each XML file token

by token, this trivial parallelization should lead to an

efficient speed-up of the compression and of the

decompression. However, typically the encodings-

based compressors reach a weaker compression ratio

than the compressors of the class of the schema-

based compressors, to which e.g. XSDS belongs to.

XQzip (Cheng and Ng, 2004), the approaches

presented in (Adiego et al., 2004) and (Buneman et

al., 2003), and the BPLEX algorithm (Busatto et al.,

2005) belong to grammar-based compression. They

compress the data structure of an XML document by

combining identical or similar sub-trees. As these

compressors have to analyze the structure of the

XML data, it is more sophisticated to fragment the

input data in order to parallelize the compression.

Nevertheless, by separating the input data into

several fragments, a loss of compression ratio is

unavoidable, as identical or similar sub-trees that are

contained in different fragments cannot be detected.

Schema-based compression comprises such

approaches as XCQ (Ng et al., 2006), XAUST

(Subramaniam and Shankar, 2005), Xenia (Werner

et al., 2006) and (Böttcher et al., 2007). They

subtract the given schema information from the

structural information. Instead of a complete XML

structure stream or tree, they only generate and

output information not already contained in the

schema information (e.g., the chosen alternative for

a choice-operator or the number of repetitions for a

*-operator within the DTD). As they all follow the

same idea as XSDS that was examined in this paper,

we assume that the ideas of parallelization can be

applied to all these approaches to enhance their

compression and decompression speed.

6 SUMMARY

AND CONCLUSIONS

Whenever web servers provide huge amounts of

XML data that are further processed by queries

within client applications, then transferring the XML

data in a compressed, but queriable data format from

the sever to the clients may significantly reduce the

amount of data transfer. When, by using a queriable

compressed XML format, XML compression or

decompression time becomes a bottleneck, parallel

XML compression and parallel decompression may

be of significant advantage. We have contributed an

approach to parallelize XML compression and

decompression using the XSDS compressor. The

XSDS compressor has the advantages that it

generally reaches stronger compression ratios than

other compressors like gzip, bzip2, and XMill, and,

in contrast to these compressors, XSDS not only

supports XPath queries on compressed XML data,

but XPath queries can also be evaluated on XSDS

compressed data even faster than on uncompressed

XML. To overcome a previous weakness of the

XSDS processor, i.e. its slower compression and

decompression, we have proposed a parallel

approach to XSDS-based XML compression. Our

approach consists of a String-search-based technique

to split an XML document into fragments and to

enrich these fragments with meta-data, such that

each of the resulting packages can be compressed in

parallel and completely independently of the other

packages. We have further shown how to extend the

approach to allow parallel decompression of XSDS-

compressed XML documents. Finally, our

experiments have shown that our approach to

parallelized XSDS compression can speed-up the

compression time by a factor of 1.4 and can speed-

up the decompression time even by a factor of up to

7 on a quad-core processor.

We assume that our approach is not limited to

parallel compression and decompression of XSDS,

but can also be applied to other schema-based XML

compression techniques like e.g. XENIA or XCQ.

To summarize, as parallel XSDS it the fastest

compressor generating a queriable compressed data

format, and additionally achieves the best

compression strength on large XML files (except for

serial XSDS), we consider our parallel XSDS to be a

significant contribution to the field of providing

compressed data in web-based information systems.

REFERENCES

Adiego, J., Navarro, G., & Fuente, P. d. (2004). Lempel-

Ziv Compression of Structured Text. Data

Compression Conference (S. 112-121). Snowbird, UT,

USA: IEEE Computer Society.

Adler, M. pigz - A parallel implementation of gzip for

modern multi-processor, multi-core machines.

http://www.zlib.net/pigz/.

Arion, A., Bonifati, A., Manolescu, I., & Pugliese, A.

(2007). XQueC: A query-conscious compressed XML

database. ACM Trans. Internet Techn. , 7 (2).

Bayardo Jr., R. J., Gruhl, D., Josifovski, V., & Myllymaki,

J. (2004). An evaluation of binary XML encoding

Schema-basedParallelCompressionandDecompressionofXMLData

optimizations for fast stream based xml processing. In

S. I. Feldman, M. Uretsky, M. Najork, & C. E. Wills

(Hrsg.), Proceedings of the 13th international

conference on World Wide Web (S. 345-354). New

York, NY, USA: ACM.

Böttcher, S., Hartel, R., & Heindorf, S. (2012). XPath

evaluation for Schema-compressed XML data. To

appear in: Australasian Database Conference (ADC

2012). Melbourne, Australia.

Böttcher, S., Hartel, R., & Messinger, C. (2010).

Searchable Compression of Office Documents by

XML Schema Subtraction. Database and XML

Technologies - 7th International XML Database

Symposium, XSym 2010 (S. 103-112). Singapore:

Springer.

Böttcher, S., Hartel, R., & Weber, S. (2012). Efficient

String-based XML Stream Prefiltering. To appear in:

Australasian Database Conference (ADC 2012).

Melbourne, Australia.

Böttcher, S., Steinmetz, R., & Klein, N. (2007). XML

index compression by DTD subtraction. ICEIS 2007 -

Proceedings of the Ninth International Conference on

Enterprise Information Systems, Volume DISI, (S. 86-

94). Funchal, Madeira, Portugal.

Buneman, P., Grohe, M., & Koch, C. (2003). Path Queries

on Compressed XML. Proceedings of 29th

International Conference on Very Large Data Bases

(S. 141-152). Berlin, Germany: Morgan Kaufmann.

Busatto, G., Lohrey, M., & Maneth, S. (2005). Efficient

Memory Representation of XML Documents.

Database Programming Languages, 10th

International Symposium, DBPL 2005 (S. 199-216).

Trondheim, Norway: Springer.

Cheney, J. (2001). Compressing XML with Multiplexed

Hierarchical PPM Models. Proceedings of the IEEE

Data Compression Conference (DCC 2001) (S. 163).

Snowbird, Utah, USA: IEEE Computer Society.

Cheng, J., & Ng, W. (2004). XQzip: Querying

Compressed XML Using Structural Indexing.

Advances in Database Technology - EDBT 2004, 9th

International Conference on Extending Database

Technology (S. 219-236). Heraklion, Crete, Greece:

Springer.

Gilchrist, J. Parallel BZIP2 (PBZIP2).

http://compression.ca/pbzip2/.

Girardot, M., & Sundaresan, N. (2000). Millau: an

encoding format for efficient representation and

exchange of XML over the Web. Computer Networks ,

33, 747-765.

Howard, P. G., & Vitter, J. S. (1996). Parallel Lossless

Image Compression Using Huffman and Arithmetic

Coding. Inf. Process. Lett. , 59, 65-73.

Liefke, H., & Suciu, D. (2000). XMILL: An Efficient

Compressor for XML Data. Proceedings of the 2000

ACM SIGMOD International Conference on

Management of Data (S. 153-164). Dallas, Texas,

USA: ACM.

Min, J.-K., Park, M.-J., & Chung, C.-W. (2003). XPRESS:

A Queriable Compression for XML Data. In A. Y.

Halevy, Z. G. Ives, & A. Doan (Hrsg.), Proceedings of

the 2003 ACM SIGMOD International Conference on

Management of Data (S. 122-133). San Diego,

California, USA: ACM.

Ng, W., Lam, W. Y., Wood, P. T., & Levene, M. (2006).

XCQ: A queriable XML compression system. Knowl.

Inf. Syst. , 421-452.

Schmidt, A., Waas, F., Kersten, M. L., Carey, M. J.,

Manolescu, I., & Busse, R. (2002). XMark: A

Benchmark for XML Data Management. VLDB 2002,

Proceedings of 28th International Conference on Very

Large Data Bases, (S. 974-985). Hong Kong, China.

Subramanian, H., & Shankar, P. (2005). Compressing

XML Documents Using Recursive Finite State

Automata. In J. Farré, I. Litovsky, & S. Schmitz

(Hrsg.), Implementation and Application of Automata,

10th International Conference, CIAA 2005 (S. 282-

293). Sophia Antipolis, France: Springer.

Tolani, P. M., & Haritsa, J. R. (2002). XGRIND: A

Query-Friendly XML Compressor. Proceedings of the

18th International Conference on Data, ICDE (S. 225-

234). San Jose, CA: IEEE Computer Society.

Werner, C., Buschmann, C., Brandt, Y., & Fischer, S.

(2006). Compressing SOAP Messages by using

Pushdown Automata. 2006 IEEE International

Conference on Web Services (ICWS 2006) (S. 19-28).

Chicago, Illinois, USA: IEEE Computer Society.

Yao, B. B., Özsu, M. T., & Khandelwal, N. (2004).

XBench Benchmark and Performance Testing of XML

DBMSs. ICDE 2004, (S. 621-632).

Zhang, N., Kacholia, V., & Özsu, M. T. (2004). A

Succinct Physical Storage Scheme for Efficient

Evaluation of Path Queries in XML. Proceedings of

the 20th International Conference on Data

Engineering, ICDE 2004 (S. 54-65). Boston, MA,

USA: IEEE Computer Society.

WEBIST2013-9thInternationalConferenceonWebInformationSystemsandTechnologies