Using Grid Related Cluster Schedule Resemblance for

Energy Rescheduling

Goals and Concepts for Rescheduling of Clusters in Decentralized Energy Systems

Astrid Nieße

and Michael Sonnenschein

OFFIS - Institute for Information Technology, Escherweg 2, 26121 Oldenburg, Germany

Department for Computer Science, University of Oldenburg, 26111 Oldenburg, Germany

Keywords:

Active Distribution Grids, Energy Scheduling, Virtual Power Plants, Graph Theory.

Abstract:

Transforming the electric power system to incorporating a considerably increased share of renewable dis-

tributed generation implicates new challenges for the control of the system. To overcome the known short-

comings of centralized control, e.g. regarding scalability and robustness, a decentralized, self-organized sys-

tem of agents for generators, loads and storages is widely discussed. We focus on a dynamic aggregation of

these units to participate on current and future energy markets for both active power and new ancillary services

products. With these units participating in system services, rescheduling of units within clusters becomes a

more complex task that should reﬂect grid usage properties.

In this work, we develop grid related cluster schedule resemblance as a metric to analyze the grid usage

changes using graph theory. This metric can be used to compare different rescheduling options regarding grid

usage for both dynamic clusters of distributed energy resources and for rescheduling of static clusters like

virtual power plants. An example is used to show that this metric can be used as a separate optimization target

for the multi-criteria optimization problem of cluster rescheduling.

1 INTRODUCTION

Transforming the electric power system to incorporat-

ing a considerably increased share of renewable dis-

tributed generation implicates new challenges for the

control of the system: The control method has to cope

with many individually conﬁgured, distributed, small

generation units and with ﬂuctuation in their feed-

in. These units can form clusters to participate in en-

ergy markets - a concept well known as virtual power

plants (VPP) as presented by Bitsch, Feldmann and

Aumayr (2002) or Abarrategui, Marti and Gonzalez

(2009).

Traditional energy management relies on cen-

tralized systems to control a static set of conven-

tional power plants. The concept of VPPs mim-

ics this approach by aggregating small units to cen-

trally controlled static clusters that are able to cope

with the market barriers on nowadays energy mar-

kets. To overcome the known shortcomings of cen-

tralized control, e.g. regarding scalability and robust-

ness, a decentralized, self-organized system of agents

for small active units (generators, loads, storages) has

been proposed for several years (Kok et al., 2005),

(Dimeas and Hatziargyriou, 2007), (Jansen et al.,

2008), (Kok, 2010), (Ramchurn et al., 2012). Besides

this control concept designed for active power product

delivery, distributed units are needed to fulﬁll grid-

stabilizing tasks to effectively substitute fossil power

plants not only from an energy market point of view,

but also reﬂecting grid operation constraints. In such

a scenario, distributed energy components (both gen-

erating and consuming power) form clusters to partic-

ipate on energy markets and to fulﬁll grid-stabilizing

tasks with different requirements regarding the loca-

tion of the units in the power grid.

Market design, cluster formation for distributed units

and the task of continuous energy scheduling are the

main tasks that have to reﬂect the requirements and

effects of using distributed units for grid stabilization

purposes. This paper deals with continuous energy

rescheduling for clusters of small distributed gener-

ation units, consumers and electrical storage as de-

scribed by Nieße, Lehnhoff, Tr¨oschel, Uslar, Wiss-

ing, and Appelrath (2012). A metric is introduced to

include grid aspects in the multi-criteria optimization

problem of energy cluster rescheduling.

The rest of this paper is structured as follows:

Nieße A. and Sonnenschein M..

Using Grid Related Cluster Schedule Resemblance for Energy Rescheduling - Goals and Concepts for Rescheduling of Clusters in Decentralized

Energy Systems.

DOI: 10.5220/0004374000220031

In Proceedings of the 2nd International Conference on Smart Grids and Green IT Systems (SMARTGREENS-2013), pages 22-31

ISBN: 978-989-8565-55-6

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

First, the task of continuous cluster energy scheduling

is described, giving an insight in the optimization cri-

teria of this task and pointing out, why grid topology

matters. We then elaborate on related work regarding

rescheduling in the distribution grid and graph based

modeling of power grids. Then, a formal represen-

tation of the power grid as a weighted graph is pro-

posed, including a weighting function and a concept

for neighborhood of units within a power grid. The

ﬁfth section shows, how this concept can be used to

characterize the changed grid usage proﬁle of a clus-

ter schedule consisting of individual units’ schedules.

Finally we point out, how these characteristics of a

cluster schedule can be used for optimized election of

a new cluster schedule.

2 CONTINUOUS ENERGY

SCHEDULING

2.1 Energy Products and Schedules

In our concept, small distributed generation units and

controllable loads form clusters and bid for products

on energy markets, e.g. on nowadays day-ahead mar-

kets. The scheduling is done for a time span T (e.g. 24

hours) as set of time intervals t

(i)

(e.g. with a length

of 1 minute). For the rest of this paper indices given

in brackets and superscript form relate to the respec-

tive time intervals, whereas all other indices are sub-

scripted.

A clusterC is deﬁned as the set of aggregated units

C = {u

, ..., u

} (1)

A product p is deﬁned by the amount of energy to

be delivered e

(i)

for each time interval t

(i)

as follows

(with T

(p)

as set of all time intervals that the product

p spans):

p : T

(p)

→ R, p(t

(i)

) = e

(i)

(2)

(p)

⊂ T, T

(p)

= {t

(i)

, ..., t

max

)

} (3)

To realize a product, operation schedules os for each

cluster unit u are generated, reﬂecting the amount of

energy delivered or used by a unit (e

(i)

) and the costs

for this amount of energy (c

(i)

) for each time interval

(i)

(e.g. each minute of a day) for this speciﬁc unit:

: T → R

, os

(i)

) = (e

(i)

, c

(i)

) (4)

The set of operation schedules of all units u that are

part of a cluster C is deﬁned as:

OS = {os

∈ C} (5)

A cluster schedule cs assigns an operation sched-

ule os

to each unit u

within the cluster:

cs : U → OS, cs(u

) = os

(6)

Following this cluster schedule, the product is ful-

ﬁlled, when the sum of power contributions by all

cluster units meets the product deﬁnition in each time

interval.

2.2 Incidents and the Need

for Rescheduling

Between market matching and product delivery

though, several incidents may render the operation

schedules infeasible. We distinguish three types of

incidents:

• Changed ReactivePower Behavior. When small

and distributed energy units are used for grid-

stabilizing issues, e.g. reactive power delivery,

hard real-time constraints have to be fulﬁlled. Re-

quirements like this e.g. for a ﬁxed cos φ are de-

ﬁned in national grid codes (e.g. (VDE, 2011) for

generating units in the low voltage level). In our

concept, we deﬁne such requirements in a more

dynamic fashion depending on the current grid

state as described by Gandor, Blank and Lehnhoff

(2012). A changed reactive power behavior may

lead to a changed active power proﬁle. There-

fore this incident type can affect the active power

contribution without notiﬁcation, although an in-

creased risk for such incidents might be known in

advance from the unit’s reactive power behavior

conﬁguration.

• Changed Active Power Behavior. Prognosis

faults regarding active power feed-in behavior

are typical for ﬂuctuating renewable energy re-

sources. Prognosis quality rises with decreasing

time to delivery. The same holds for prognoses

regarding the behavior of controllable and non-

controllable loads.

• Unit Failure. With a high share of distributed

and small units in such a system, unit failure with

preliminary notiﬁcation (e.g. for maintenance) or

without (e.g. breakdown) has to be considered.

Incidents of these types may render the delivery of

the power product infeasible, thus raising the need for

rescheduling, i.e. generating new and valid operation

schedules for some of the units within the cluster.

2.3 Requirements and Goals for

Rescheduling

Generating a new cluster schedule has to reﬂect sev-

eral requirements:

UsingGridRelatedClusterScheduleResemblanceforEnergyRescheduling-GoalsandConceptsforReschedulingof

ClustersinDecentralizedEnergySystems

First, the power product has to be delivered as con-

tracted at the market. Although an exact delivery

may not be possible, the new cluster schedule should

minimize the deviation in active power delivery. It

should not be possible to trade off product delivery

costs against current balancing energy costs that have

to be paid in case of prognosis deviations. The Ger-

man energy market e.g. prevents such a tradeoff by

deﬁning a lower margin for balancing energy costs

by the current power price on energy markets (Bun-

desnetzagentur, 2012).

Second, the additional costs that emerge from recon-

ﬁgurating the units within the cluster should be min-

imized, i.e. by minimizing the sum of reconﬁgura-

tion costs and the difference between costs for old

and new schedule execution. This requirement may

be weighed against the robustness of the new clus-

ter schedule: If rescheduling comes with additional

costs, the new schedule should be tolerant to addi-

tional incidents.

When a product is contracted at the market, the re-

sulting usage of the power grid has to be tested for ad-

missibility. Abarrategui, Marti and Gonzalez (2009)

perform a check for admissibility after market match-

ing, whereas Khattabi, H¨ubner, Kießling and Braun

(2012) propose a check before market matching to

adapt grid charges accordingly. In both concepts, sev-

eral grid calculations and load ﬂow analyses have to

be performed. We expect, that for continuous energy

scheduling, these calculations cannot be performed in

any case for reasons of time constraints and lack of

(dynamic) information on the grid state. Neverthe-

less, the reconﬁguration of units may lead to critical

grid states regarding utilization and remaining trans-

mission capacity of lines and transformers. Critical

grid states have been a topic in transmission grids for

a long time, and with more and more distributed gen-

eration this has to be reﬂected for the distribution grid

as well. Demand side management additionally may

aggravatethis as simultaneity factors may change dra-

matically as analyzed by Gwisdorf, Stepanescu and

Rehtanz (2010).

Therefore we propose to reﬂect the grid when set-

ting up a new schedule and to maximize the resem-

blance of the schedules regarding the utilization of the

grid, thus minimizing the risk for critical grid states,

when admissibility checks cannot be performed in

time.

The goals for rescheduling can be summarized as

follows:

• Deliver active power product as contracted,

• minimize additional costs emerging from

rescheduling and reconﬁguration of units,

• maximize robustness of new cluster schedule and

• minimize changes in the usage of the power grid.

In the following sections a concept to reﬂect the

power grid related optimization target for continuous

energy scheduling is presented. As can be seen from

the goals above, this is part of a multi-criteria opti-

mization problem. We aim to deﬁne the grid related

optimization target as a separate target that does not

have dependencies to other targets, especially regard-

ing the number of reconﬁgurations (i.e. the number

of units that need to be adapted in their operating

behavior) needed: Weighting of the optimization tar-

gets might change over time, as – when there is still

enough time until product delivery – cost optimiza-

tion regarding the units might override robustness.

When the grid state is considered critical though, we

might prioritize these aspects over costs. Therefore

we want to decouple the grid related metric from the

other optimization targets.

3 RELATED WORK

This section deals with related work for rescheduling

of units in the distribution grid and - as a means to

achieve this - for analyzing the power grid using ap-

proaches from graph theory. An overview on related

work regarding dynamic aggregation of energy units

in the distribution grid is given by Nieße et al. (2012).

In contrast to the transmission grid, where a con-

tinuous measurement allows to detect violations of

grid operational constraints, no such infrastructure is

installed in the distribution grid, especially on the low

voltage level. Moreover, due to the large amount of

units in the distribution grid, the identiﬁcation of the

most efﬁcient unit to avoid a critical grid state can-

not be deduced manually. Additionally, the under-

lying optimization problem of identifying the most

efﬁcient mitigation actions is challenging due to the

non-linearity and non-differentiability of the underly-

ing power ﬂow equations as shown by Handschin, Re-

htanz, Wedde, Krause and Lehnhoff (2008). There-

fore, state-of-the-art control systems on the transmis-

sion level cannot be transferred directly to the lower

voltage levels due to (a) lack of real-time information

and (b) enlarged complexity of the redispatch prob-

lem.

In recent years, a lot of work has been done to

develop control schemes appropriate to the distribu-

tion grid structure that overcome these problems like

e.g. the work done by Krause and Lehnhoff (2012).

A generalized static state estimation method is pre-

sented that is valid for power grids with missing in-

put data. Neusel-Lange, Oerter and Zdrallek (2012)

SMARTGREENS2013-2ndInternationalConferenceonSmartGridsandGreenITSystems

present an approach for low voltage state identiﬁ-

cation and control handling the problem of missing

data as well - the state estimation and control algo-

rithm presented adds prediction of loads and feed-

in for units lacking appropriate measurements. An

established algorithm for power ﬂow can thus han-

dle real-time data and - if these are unachievable -

predicted values (Neusel-Lange et al., 2012). These

methods build on real-time information on the grid

state, adding up substitute values for missing data.

For the approach presented in this work, we try to

choose rescheduling options without real-time infor-

mation for two reasons: First, as Blank, Gerwinn and

Krause (2011) could show, identifying the most efﬁ-

cient redispatch from the huge amount of possible dis-

patch options is in itself a complex task . It is not yet

clear how this approach could be integrated directly

in a multi criteria problem covering other constraints

like robustness and costs. Second, our concept is in-

tegrated in a market-based concept for active power

products from dynamic clusters of distributed energy

units. With the underlying process, a grid admissi-

bility check is performed after market matching. We

build on the results of that check and try to identify

schedules that resemble the initial schedules regard-

ing the grid usage using a graph-based approach.

The work of Barabasi and Albert (1999) and Al-

bert, Jeong and Barabasi (2000) regarding the struc-

tural analysis of complex networks using graph theory

has gained wide attention in the vulnerability anal-

ysis of power grids on the transmission level (Al-

bert et al., 2004), (Holmgren, 2006), (Hines et al.,

2010), (Schneider et al., 2011), (Chopade and Bik-

dash, 2011), (Wang et al., 2012). The transmission

grid is transferred to a graph representation with the

generators and loads as nodes in the graph and dif-

ferent concepts for generating the edges. Whereas

Holmgren (2006) and Chopade and Bikdash (2011)

generate the links as found in the grid topology,Hines

and Blumsack (2010)and Wang (2012) connect nodes

using the electrical distance of nodes to better re-

ﬂect the engineering characteristics of the grid within

the graph structure by choosing a threshold to distin-

guish connected from unconnected nodes that yields

the known number of links (i.e. busses in the power

grid). The latter approach showed good results for

the vulnerability analysis of power grids using struc-

tural metrics like cluster coefﬁcients or degree dis-

tribution. Dynamic effects in the transmission grids

have been analyzed by Kinney, Crucitti, Albert and

Latora (2005) for cascading failure analysis. They

added weights to the edges of a node representing the

efﬁciency of a line, with an efﬁciency of 0 prohibiting

paths using that line and 1 meaning full usage of that

line is possible. The efﬁciency concept and its trans-

fer to shortest path detection is discussed in detail in

section 4.2.

Nguyen, Kling and Ribeiro (2011) solved a dis-

tributed control task in the power distribution grid us-

ing the graph representation as described in Nguyen,

Kling and Myrzik (2010). The power distribution grid

is represented using a graph with the edges represent-

ing the lines in the grid. Using this representation,

an optimal power ﬂow problem is solved in a distri-

bution grid scenario. Whereas the structural vulnera-

bility analysis has no need for generating a weighted

graph, in this study on the dynamic usage of the grid

weights are added to the edges reﬂecting the currently

measured power ﬂows. So for this approach, detailed

system knowledge including both static and dynamic

data is required.

4 REFLECTING THE GRID

TOPOLOGY

As pointed out in section 3, power grids have been

modeled as graphs for several applications by assign-

ing a graph node to generating and power consuming

units to model the grid connection node. In this sec-

tion we apply and extend this concept in such a way,

that it can be used for rescheduling of energy clus-

ters with the optimization goal of identifying a sched-

ule that leads to a similar grid usage as the original

schedule. First, we pinpoint some design decisions

for modeling the power grid as a graph. After that,

a weighting function for edges in this graph is de-

veloped, that is needed to interrelate a change in the

schedule to a change in the usage of the power grid.

Using this extended model, the changed grid charac-

teristics of a new schedule are deﬁned in section 5.

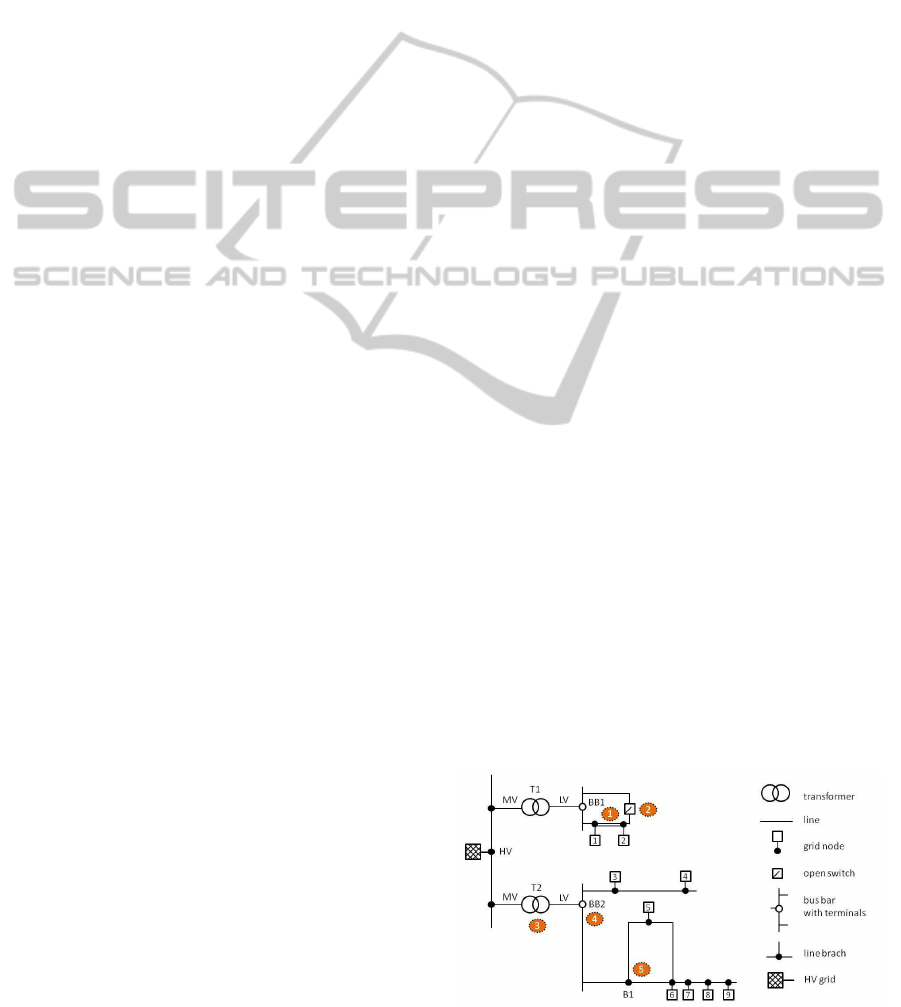
The power grid is transformed to an undirected

graph G = (V, E) with V = {v

, ..., v

} representing

the vertices (the grid connection nodes with the gen-

erating and consuming units annotated to that node)

and E = {e

, ..., e

} representing the edges between

Figure 1: Simple example grid.

UsingGridRelatedClusterScheduleResemblanceforEnergyRescheduling-GoalsandConceptsforReschedulingof

ClustersinDecentralizedEnergySystems

this nodes, i.e. the lines of the power grid. A unit u

assigned to a node v

by the grid node assignment gn:

gn : U → V, gn(u

) = v

(7)

A simpliﬁed example of a medium voltage level

grid is shown in ﬁgure 1. The following design de-

cisions were chosen to generate the graph from this

matrix (enumeration refers to labeled number in ﬁg-

ure 1):

1. Multiple Lines between Nodes. No multiple

edges are modeled. The edge between nodes

1 und 2 for example, probably strengthened by

adding a parallel line, is modeledas a simple edge.

2. Open Switches. Lines that are electrically dis-

connected by open switches are not modeled.

3. Voltage Level Transitions. Transformers are

modeled as separate nodes in the graph.

4. Bus Bars. Bus bars are modeled as nodes that

may be connected to several nodes in the graph.

Thus, the degree of node BB2 is deg(BB2) = 3,

whereas BB1 has deg(BB1) = 2, as no node will

be modeled between BB1 and the open switch

(see ﬁgure 1).

5. Line Branching. Line branching is modeled as

separate node. Branch B1 has a degree deg(B1) =

As a consequence, we distinguish three types of nodes

that form the set V: Transformer nodes (set TN), bus

bar nodes (set BB) and normal grid nodes (set GN).

V = TN

[

GN (8)

The artiﬁcial line branching nodes inserted in the

graph are deﬁned as normal grid nodes.

4.1 Weighting Function

The weights added to an edge in the resulting graph

should allow to reﬂect the change of voltage levels in

paths to prevent schedules with compensation strate-

gies in completely different parts of the grid. In ﬁg-

ure 2 this is illustrated with different paths within the

graph derived from the example grid in ﬁgure 1. We

take a closer look at path

1,3

and path

3,9

. Both paths

contain six edges. If only path length is considered,

the neighborhoodrelation between the nodes is identi-

cal. In power systems though, changes between volt-

age levels include conversion losses and - different

from social networks or other complex systems that

may be represented using graph theoretical concepts

- distance (edge length) matters. Using the electrical

distance for the weighting function has be done by

Nguyen, Kling and Ribeiro (Nguyen et al., 2011). We

propose a different approach that allows conﬁguration

with less system information by deﬁning weights for

different types of edges that can be adapted dynami-

cally.

An edge e = v

is of type

• cvl (change of voltage level), if v

∈ TN ∧v

∈ BB,

noted as e

cvl

, with E

cvl

= {e

cvl

= v

| v

∈ TN ∧

∈ BB},

• be (bus bar edge), if v

∈ BB∧v

∈ GN, noted as

, with E

= {e

= v

| v

∈ BB ∧ v

∈ GN},

• ne (normal edge), if (v

∈ GN ∧ v

∈ GN) ∨

∈ TN ∧ v

∈ TN), noted as e

, with E

= v

| (v

∈ GN ∧ v

∈ GN) ∨ (v

∈ TN ∧

∈ TN)}

The time-dependent weighting function w assigns a

weight w

∈ [0, 1] to each edge from E depending on

time interval and edge type:

w : E × T

(p)

→ [0, 1] (9)

subject to:

cvl

(i)

) = tw

(10)

(i)

) = bbw

(11)

(i)

) = nw

(12)

denoting that the weighting function w might deliver

different values (either tw

, bbw

or nw

) depending

on the edge type subset of E(either E

cvl

, E

or E

With this concept, in a system with dynamic informa-

tion (e.g. regarding power ﬂow), the weighting func-

tion can be adapted dynamically to reﬂect properties

relevant for the actual phenomena in the power grid

analyzed. If no such information is given, a simple

static conﬁguration can be chosen for tw

, bbw

and

. Especially in distribution grids, where dynamic

measurement information on the grid and the units

connected to the grid cannot be retrieved, a static con-

ﬁguration could help to approximate a reﬂection of

grid constraints. Some details on how these weights

should be chosen are given in the next section.

4.2 Neighborhood and Shortest Path

To identify the shortest path between two vertices, a

neighborhood function compliant with the following

requirements derived from the optimization goals for

continuous scheduling (see section 2.3) is needed:

1. Requirement 1 – Distinguish Local and Wide-

area Compensation. Paths within the same volt-

age level that differ in the number of edges should

be differentiated by the neighborhood function.

With this requirement, local compensation of in-

cidents (e.g. at the neighboring node) should be

SMARTGREENS2013-2ndInternationalConferenceonSmartGridsandGreenITSystems

distinguishable from wide-area compensation. In

the example given in 1, an incident occurring at

node 8 should preferably get compensated at node

7 or 9.

2. Requirement 2 – Transition of Voltage Levels.

Paths that have the same number of contained

edges should be distinguishable if they differ re-

garding the voltage level proﬁle. Thus it should

be possible to prefer new schedules that compen-

sate incidents within the same voltage level of a

distribution grid or vice versa.

3. Requirement 3 – Allow Exclusion of Single

Lines. It should be possible to set the weight of

single edges in such a way that all paths using this

edge are prohibited for scheduling. Thus, conges-

tion management with both spatial and temporal

differentiation should be possible.

To reﬂect requirement 2 (transition of voltage levels),

the following has to be valid when choosing values

for the weights tw

, bbw

and nw

for all time intervals

(i)

≤ bbw

< nw

(13)

Choosing the same weight for tw

and bbw

is pos-

sible, but preferring paths within one voltage level

(requirement 2) can only be done when the normal

edges’ weight is greater than the bus bar crossing and

transformer edges’ weight.

A weight of 0 annotated to an edge depicts that

the line represented by this edge is prohibited for

rescheduling (requirement 3), i.e. the parts of the

graph that can only be reached using this edge must

not be affected by rescheduling.

For the upcoming examples, the following

weights are chosen for the different edge types: tw

0.7, bbw

= 0.8, nw

= 1.0 for all time intervals t

(i)

Figure 2 illustrates different paths with these

weights annotated to the edges.

Figure 2: Exemplary paths with weights and voltage levels.

The set of paths between v

and v

Path

(i, j)

is de-

ﬁned as follows:

Path

(i, j)

= {(v

, v

i+1

, ..., v

) |

∃ x : e

= v

x+1

∈ E, i ≤ x < j}

(14)

A speciﬁc path is therefore an element from this set.

path

(i, j),k

∈ Path

(i, j)

(15)

To deﬁne distinct paths in the graph, paths have to be

deﬁned by naming the series of incident nodes in the

path. To simplify this for the upcoming examples, we

deﬁne some paths used in the text as follows with the

notation path

i, j

path

1,3

: 1 - BB1 - T1 - HV - TN - BB2 - 3

path

3,9

: 3 - BB2 - B1 - 6 - 7 - 8 - 9

path

B1,9

: B1 - 6 - 7 - 8 - 9

path

6,9

: 6 - 7 - 8 - 9

Within deﬁnitions, we will use the notation

path

(i, j),k

so that we can distinguish different paths

between v

and v

by k where needed.

We propose the harmonic composition w

harm

of all

weights of the edges contained in the path to evaluate

neighborhood as used by Kinney et al. for power grid

graph analyses (Kinney et al., 2005). The harmonic

composition of a set of numbers X = {x

, x

, ..., x

} is

deﬁned as

harm

(X) =

(

0 ∀X : ∃x ∈ X : x = 0

∑

else

(16)

In table 1 the harmonic composition is compared

to arithmetic mean and harmonic mean for example

paths in the example grid. We do not compare the har-

monic composition to simply summing up the weights

of the edges, as requirement 3 (exclusion of single

lines) cannot be fulﬁlled by such an approach.

The above example of paths path

1,3

and path

3,9

illustrates, that requirement 2 is fulﬁlled using this

metric: w

harm

(path

1,3

) = 0.136. The neighborhood

value of path

3,9

is w

harm

(path

3,9

) = 0.154. Thus, a

path within the same voltage level can be differen-

tiated from a path crossing voltage levels as long as

the weights are differentiated as shown above. This

metric is deﬁned 0 if the weight of one of the con-

tained edges is set to 0 (requirement 3). Therefore this

metric shows advantages to the arithmetic mean that

would not reﬂect this aspect. Further, the harmonic

composition reﬂects the number of edges within the

path (requirement 1) not reﬂected by arithmetic or

harmonic mean: With each weight of edges set to

1.0, a path with 3 edges (e.g. path

6,9

) would yield

harm

(path

6,9

) = 0.333, whereas a path with 4 edges

(e.g. path

B1,9

) would yield w

harm

(path

6,9

) = 0.25.

UsingGridRelatedClusterScheduleResemblanceforEnergyRescheduling-GoalsandConceptsforReschedulingof

ClustersinDecentralizedEnergySystems

Table 1: Metric comparison for exemplary paths.

path

1,3

path

3,9

path

6,9

path

B1,9

# edges 6 6 3 4

arithm. 0.833 0.933 1 1

harm. 0.816 0.923 1 1

harm

0.136 0.154 0.333 0.25

The neighborhood value neigh

(i)

i, j

of two nodes v

and v

on path

(i, j),k

in time interval t

(i)

is therefore

deﬁned as follows (please note that the neighborhood

deﬁnition is time-dependent, as the weighting func-

tion used is time-dependent as well):

neigh

(i)

i, j

(path

(i, j),k

) = w

harm

(i)

path

(i, j),k

) (17)

where:

(i)

path

(i, j),k

= {w(e

(i)

) |

∃ x : e

= v

x+1

∈ E, i ≤ x < j}

(18)

The shortest path sp

i, j

between nodes v

und v

time interval t

(i)

is now deﬁned as the path with the

highest neighborhood value following equation 17:

path

(i, j),k

= sp

(i)

i, j

(19)

subject to:

∀path

(i, j),m

, m 6= k :

neigh

(i)

i, j

(path

(i, j),m

) < neigh

(i)

i, j

(path

(i, j),k

)

(20)

4.3 Adding the Grid View to Cluster

Schedules

To analyze the change in power grid usage with a new

cluster schedule, we ﬁrst have to translate it to a node

related schedule that aggregates the power behavior

of units to the node they are assigned to. We deﬁne

the node related schedule ns

for each time interval as

follows:

ns : T− > R, ns

(i)

) =

∑

∈C

(i)

(21)

subject to (see deﬁnition 7):

gn(u

) = v (22)

Let NS be the set of all node schedules for a clus-

ter (i.e. nodes with units within the cluster), then the

cluster node schedule cns maps a node to its node

schedule:

cns : V → NS, cns(v

) = ns

(23)

In the example grid, a maximum of one unit is as-

signed to each node for the sake of conceptual clarity.

Unit and node can thus be referred to with the same

number in the explaining text. Therefore, the energy

entries in the cluster schedules are equivalent to the

cluster node schedule throughout the rest of this pa-

per.

5 USING GRID RELATED

CLUSTER SCHEDULE

RESEMBLANCE FOR ENERGY

RESCHEDULING

With the grid characteristics of a cluster schedule as

deﬁned in the last section, an optimized rescheduling

can reﬂect grid characteristics besides other optimiza-

tion goals as costs and robustness. To implement this,

we deﬁne grid-related resemblance of cluster sched-

ules and give an example of how this can be used to

choose a new cluster schedule from a set of possible

rescheduling options.

5.1 Rescheduling and Comparison of

Grid Characteristics

We deﬁne two cluster schedules to be grid-related

identical, if their cluster node schedules are identical,

i.e. rescheduling only affects units assigned to the

same grid node.

The grid-related cluster schedule resemblance

gr(cs

∗

) of a new cluster schedule cs

∗

with the original

cluster schedule cs is deﬁned as follows (with v

inc

node where at least one unit affected by an incident

is connected and sp

inc,k

as shortest path between v

inc

and v

as deﬁned in deﬁnitions 19 and 20):

gr(cs

∗

) =

∑

(i)

∈T

(p)

∑

∈G

· w

(i)

inc,k

∑

(24)

where:

(i)

inc,k

= neigh

(i)

inc,k

(sp

(i)

inc,k

) · |ns

(i)

− ns

∗(i)

| (25)

The dynamic weighting factor β

can be used to

reﬂect time intervals within a day where schedule de-

viations are considered more critical. For the rest of

this paper β

is set to 1 for all time intervals and thus

has no effect. The evaluation on the effect of this fac-

tor is subject to future work.

SMARTGREENS2013-2ndInternationalConferenceonSmartGridsandGreenITSystems

5.2 Example: Choosing a New Cluster

Schedule using Grid-related Plan

Resemblance

For the grid example given above, an original

cluster schedule was chosen for the cluster C =

{u1, u2, u3, u6, u7, u8} for one time interval. For this

interval, an incident occurs at unit 2 decreasing the

original power production from 4 to 1. In table 2,

an excerpt of possible new schedules is given. All

of these possible new cluster schedules fulﬁll the re-

quirement, that power delivery sums up to 25. In

ﬁgure 3 and ﬁgure 4 the units compensating the in-

cident when using schedules 1 or 2 are marked to

illustrate the topological dimension of the schedule

change. Please note, that the energy related change in

the schedule can only be deduced from table 2. Both

dimensions are used for grid related cluster schedule

resemblance.

Table 2: Original and potential new cluster schedules.

orig sched1 sched2 sched3 sched4

u2 4 1 1 1 1

u1 1 4 3 3 3

u3 4 4 1 5 4

u6 6 6 6 6 6

u7 5 5 8 5 5

u8 5 5 6 5 6

∑

25 25 25 25 25

Figure 3: Following schedule 1 a directly neighbored unit

is used to compensate the incident at unit 2.

Table 3: Characteristics of new cluster schedules.

sched1 sched2 sched3 sched4

# reconf. 1 4 2 2

gr(cs

∗

) 0.6 0.533 0.421 0.416

The grid related cluster schedule resemblance as

deﬁned in equation 24 is listed in table 3. Schedule 1

compensates the incident at unit 2 occurring at node

Figure 4: With schedule 2 the incident at unit 2 would get

compensated by several units located even in a separate LV

grid.

2 at the directly neighbored node 1 using unit 1 with-

out crossing more than one edge and within the same

voltage level (see ﬁgure 3). This plan has the highest

grid-related cluster schedule resemblance. Schedule

2 (see ﬁgure 4) has the highest number of reconﬁg-

urations, but grid resemblance is high nevertheless.

Schedules 3 and 4 come with a small number of re-

conﬁgurations but compensate with stark changes at

the most distant grid nodes. It can be seen, that grid

related cluster schedule resemblance decouples the

amount of reconﬁgurations needed for compensation

(as a cost-relevant aspect) and grid characteristics of

a plan.

6 CONCLUSIONS AND FUTURE

WORK

In this paper we propose grid-related cluster schedule

resemblance as a new metric to compare schedules

for clusters of distributed energy generators and con-

sumers regarding their grid usage proﬁle changes. It

was shown that this metric can decouple the amount

of reconﬁgurations needed for compensation (as a

cost-relevant aspect) and grid characteristics of a plan.

Therefore grid related cluster schedule resemblance

can be used as a separate optimization target in the

multi-criteria optimization problem of energy cluster

rescheduling that deals with costs and other targets as

well.

In future work we will compare the results from

this metric with conventionalload ﬂow calculations to

evaluate, if the schedules chosen using the metric lead

to less critical grid operation regarding operational

constraints of transformers and lines. If the metric

developed in this work thus shows to be appropriate

as a means to reﬂect grid constraints in reschedul-

ing distributed energy units, we will apply this ap-

proach to evaluate multi-dimensional schedules e.g.

for rescheduling of clusters active on day-ahead mar-

UsingGridRelatedClusterScheduleResemblanceforEnergyRescheduling-GoalsandConceptsforReschedulingof

ClustersinDecentralizedEnergySystems

kets combined with cost and robustness. We will inte-

grate this optimization in a distributed constraint op-

timization problem to adapt schedules to unforeseen

incidents on distributed power generation and usage.

ACKNOWLEDGEMENTS

The Lower Saxony research network ‘Smart Nord’

acknowledges the support of the Lower Sax-

ony Ministry of Science and Culture through the

“Nieders¨achsisches Vorab” grant programme (grant

ZN 2764).

Furthermore, we thank Sebastian Lehnhoff and

the anonymous reviewers for helpful comments to im-

prove this paper.

REFERENCES

Abarrategui, O., Marti, J., and Gonzalez, A. (2009). Con-

structing the Active European Power Grid. In Pro-

ceedings of WCPEE09, pages 1–4, Cairo.

Albert, R., Albert, I., and Nakarado, G. L. (2004). Struc-

tural Vulnerability of the North American Power Grid.

Physical Review E, 69(025103(R)):1–10.

Albert, R., Jeong, H., and Barabasi, A. (2000). Error

and attack tolerance of complex networks. Nature,

406(6794):378–82.

Barab´asi, A. and Albert, R. (1999). Emergence of Scaling

in Random Networks. Science, 286(5439):509–512.

Bitsch, R., Feldmann, W., and Aumayr, G. (2002). Virtuelle

Kraftwerke - Einbindung dezentraler Energieerzeu-

gungsanlagen. etz, 9.

Blank, M., Gerwinn, S., Krause, O., and Lehnhoff, S.

(2011). Support vector machines for an efﬁcient repre-

sentation of voltage band constraints. 2011 2nd IEEE

PES International Conference and Exhibition on In-

novative Smart Grid Technologies, pages 1–8.

Bundesnetzagentur (2012). Amtsblatt 21/2012 der Bun-

desnetzagentur, Beschluss BK6-12-024.

Chopade, P. and Bikdash, M. (2011). Critical infrastructure

interdependency modeling: Using graph models to as-

sess the vulnerability of smart power grid and SCADA

networks. 2011 8th International Conference & Expo

on Emerging Technologies for a Smarter World, pages

1–6.

Dimeas, A. L. and Hatziargyriou, N. (2007). Agent based

control of Virtual Power Plants. In Internation Con-

ference on Intelligent System Applications to Power

Systems, pages 1–6, Toki Messe, Niigata.

Gandor, M., Blank, M., and Lehnhoff, S. (2012). Reconﬁg-

uration Strategies for Electrical Devices for Operation

within Feasibility Margins. In VDE-Kongress 2012

Smart Grid, Stuttgart. VDE Verlag GmbH.

Gwisdorf, B., Stepanescu, S., and Rehtanz, C. (2010). Ef-

fects of Demand Side Management on the Planning

and Operation of Distribution Grids. In Innovative

Smart Grid Technologies Conference Europe (ISGT

Europe), 2010 IEEE PES.

Handschin, E., Rehtanz, C., Wedde, H. F., Krause, O., and

Lehnhoff, S. (2008). On-line stable state determi-

nation in decentralized power grid management. In

Proceedings of the 16th Power Systems Computation

Conference (PSCC’08), pages 07–14, Glasgow, Scot-

land, UK.

Hines, P., Blumsack, S., Sanchez, E. C., and Barrows, C.

(2010). The Topological and Electrical Structure of

Power Grids. 2010 43rd Hawaii International Con-

ference on System Sciences, pages 1–10.

Holmgren, A. J. (2006). Using graph models to analyze the

vulnerability of electric power networks. Risk anal-

ysis : an ofﬁcial publication of the Society for Risk

Analysis, 26(4):955–69.

Jansen, J. C., van der Welle, A., and Nieuwenhout, F.

(2008). The virtual power plant concept from an eco-

nomic perspective: updated ﬁnal report. Technical Re-

port 0.

Khattabi, M., H¨ubner, C., Kießling, A., and Braun, M.

(2012). Distribution grid automation as the basis for

the smart energy system of the future. In VDE, edi-

tor, VDE-Kongress 2012 Smart Grid, Stuttgart. VDE

Verlag.

Kinney, R., Crucitti, P., Albert, R., and Latora, V. (2005).

Modeling cascading failures in the North Ameri-

can power grid. The European Physical Journal B,

46(1):101–107.

Kok, K. (2010). Multi-Agent Coordination in the Elec-

tricity Grid , from Concept towards Market Introduc-

tion. In Ninth Conference on Autonomous Agents and

Multiagent Systems AAMAS 2010, pages 1681–1688,

Toronto, Canada.

Kok, K., Warmer, C., Kamphuis, R., Mellstrand, P., and

Gustavsson, R. (2005). Distributed Control in the

Electricity Infrastructure. In Proceedings of the Inter-

national Conference on Future Power Systems, 2005.

Krause, O. and Lehnhoff, S. (2012). Generalized Static-

State Estimation. In 22nd Australasian Universities

Power Engineering Conference (AUPEC).

Neusel-Lange, N., Oerter, C., and Zdrallek, M. (2012).

State Identiﬁcation and Automatic Control of Smart

Low Voltage Grids. In Proceedings of the 3rd IEEE-

PES-Conference ”Innovative Smart Grid Technolo-

gies” Europe 2012, pages 1–6, Berlin, Germany.

Nguyen, P. H., Kling, W. L., and Myrzik, J. M. A. (2010).

An application of the successive shortest path algo-

rithm to manage power in multi-agent system based

active networks. European Transactions on Electrical

Power, 20(8):1138–1152.

Nguyen, P. H., Kling, W. L., and Ribeiro, P. F. (2011).

Agent-based power routing in Active Distribution

Networks. 2011 2nd IEEE PES International Confer-

ence and Exhibition on Innovative Smart Grid Tech-

nologies, pages 1–6.

Nieße, A., Lehnhoff, S., Tr¨oschel, M., Uslar, M., Wiss-

ing, C., Appelrath, H.-J., and Sonnenschein, M.

(2012). Market-based self-organized provision of ac-

tive power and ancillary services: An agent-based ap-

proach for Smart Distribution Grids. In Complexity in

Engineering (COMPENG), 2012, Aachen.

SMARTGREENS2013-2ndInternationalConferenceonSmartGridsandGreenITSystems

Ramchurn, S. D., Vytelingum, P., Rogers, A., and Jennings,

N. R. (2012). Putting the Smarts into the Smart Grid :

a Grand challenge for artiﬁcial intelligence. Commu-

nications of the ACM, 55(4):86–97.

Schneider, C. M., Ara, N. A. M., Havlin, S., and Herrmann,

H. J. (2011). Towards designing robust coupled net-

works. pages 1–7.

VDE (2011). VDE-AR-N 4105: Erzeugungsanla-

gen am Niederspannungsnetz - Technische Min-

destanforderungen f¨ur Anschluss und Parallelbetrieb

von Erzeugungsanlagen am Niederspannungsnetz.

Wang, Y., Zhao, J., Zhang, F., and Lei, B. (2012). Study on

structural vulnerabilities of power grids based on the

electrical distance. IEEE PES Innovative Smart Grid

Technologies, pages 1–5.

UsingGridRelatedClusterScheduleResemblanceforEnergyRescheduling-GoalsandConceptsforReschedulingof

ClustersinDecentralizedEnergySystems