
Personalized Thermal Comfort Forecasting for Smart Buildings via
Locally Weighted Regression with Adaptive Bandwidth
Carlo Manna, Nic Wilson and Kenneth N. Brown
Cork Constraint Computation Centre(4C), Dept. Computer Science, University College Cork, Cork, Ireland
Keywords:
Machine Learning, Smart Buildings, Thermal Comfort.
Abstract:
A personalized thermal comfort prediction method is proposed for use in combination with smart controls
for building automation. Occupant thermal comfort is traditionally measured and predicted by the Predicted
Mean Vote (PMV) metric, which is based on extensive field trials linking reported comfort levels with the
various factors. However, PMV is a statistical measure applying to large populations, and the actual thermal
comfort could be significantly different from the predicted value for small groups of people. Moreover it may
be hard to use for a real-time controller due to the number of sensor readings needed. In the present paper,
we propose Robust Locally Weighted Regression with Adaptive Bandwidth (LRAB), a kernel based method,
to learn individual occupant thermal comfort based on historical reports. Using publicly available datasets,
we demonstrate that this technique is significantly more accurate in predicting individual comfort than PMV
and other kernel methods. Therefore, is a promising technique to be used as input to adpative HVAC control
systems.
1 INTRODUCTION
Energy-efficiency for buildings is currently a topic
of major interest, especially with increasing energy
costs. In particular, the HVAC (heating ventilation
and air conditioning) system, which ensures thermal
comfort conditions in offices (during both wintertime
and summer), on the other is one of the main energy
consumers in a building. For this reason, accurately
predicting comfort levels for the occupants can en-
able one to avoid unnecessary heating or cooling, and
thus improve the energy efficiency of the HVAC sys-
tems. A number of thermal comfort indices (indica-
tors of human comfort) have been studied for the de-
sign of HVAC systems (Fanger, 1972; Gagge et al.,
1986), the most widely used of which is the Predicted
Mean Vote (PMV) index, which was developed by
Fanger (Fanger, 1972). However, to find appropri-
ate set-point temperatures with the PMV standard,
the designer has to make assumptions about cloth-
ing and activity of occupants. Moreover, for small
groups of people within a single room or zone in a
building, PMV may not perform an accurate predic-
tion as pointed out in (Kumar and Mahdavi, 2001) and
in (Humphreys and Nicol, 2000). To address these is-
sues, newer standards such as the recently accepted
revisions to ASHRAE Standard 55, that include a
new adaptive comfort standard (ACS) (de Dear and
Brager, 2002), suggests an alternative (or a comple-
mentary) theory of thermal perception based on the
psychological dimension of adaptation, which may be
particularly important in contexts where people’s in-
teractions with the environment (i.e. personal thermal
control), or diverse thermal experiences, may alter
their expectations, and thus, their thermal sensation
and satisfaction. In particular, the level of comfort
perceivedby each individual also depends on their de-
gree of adaptation to the context and to the environ-
mental changes, and therefore the specificity of each
individual should be taken into account to learn and
predict comfort satisfaction.
For these reasons, in the present paper, we pro-
pose an alternative approach tailored to individual oc-
cupants, which relies on historical data on individ-
ual responses to internal environment conditions. We
propose Robust Locally Weighted Regression (Cleve-
land, 1979) with an Adaptive Bandwidth (LRAB), a
kernel based method, to learn, automatically, the com-
fort model of each user based on their history. We ap-
plied this method using up to three input variables (in-
side air temperature, humidity and mean radiant tem-
perature) which do not require expensive sensors and
are easy to measure. Finally, we compare the pro-
posed method with both PMV and a standard kernel
32
Manna C., Wilson N. and Brown K..
Personalized Thermal Comfort Forecasting for Smart Buildings via Locally Weighted Regression with Adaptive Bandwidth.
DOI: 10.5220/0004375100320040
In Proceedings of the 2nd International Conference on Smart Grids and Green IT Systems (SMARTGREENS-2013), pages 32-40
ISBN: 978-989-8565-55-6
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

method, the Nadaraya-Watson kernel method (with
different kernel functions), using publicly available
datasets (ASHRAE, RP-884). Our experimental re-
sults show that LRAB outperforms both the PMV and
the Nadaraya-Watson kernel method in predicting in-
dividual comfort, and hence it is a promising tech-
nique to be used as an input to the heating/cooling
control systems in an office environment.
The paper is organised as follows: in the next sec-
tion, some backgroundon PMV and on alternative ex-
isting techniques are reported. Then, in section 2, the
Nadaraya-Watson kernel and the proposed method are
described, while in the section 3, the experimental re-
sults using a public dataset are shown. Finally, in sec-
tion 4, conclusions and future directions are reported.
1.1 Previous Research
Many methods have been proposed for comfort eval-
uation and prediction; a comprehensive overview is
given in (Olesen, 2004). However, as stated in the
previous section, the most widely used of these is the
PMV index, which has been an international standard
since the 1980s (ASHRAE, 2010), (ISO, 1994). The
conventional PMV model predicts the mean thermal
sensation vote on a standard scale for a large group
of people in a given indoor climate. Like the other
methods described in (Olesen, 2004), it is a function
of two human variables and four environmental vari-
ables, i.e. clothing insulation worn by the occupants,
human activity, air temperature, air relative humidity,
air velocity and mean radiant temperature. The values
of the PMV index have a range from -3 to +3, which
corresponds to an occupant’s thermal sensation from
cold to hot, with the zero value of PMV meaning neu-
tral. As mentioned above, PMV is not just an index
to measure the comfort level, but it is also, and espe-
cially, a model to predict the thermal sensation given
the indoor environmental conditions. It has been val-
idated by many studies, both in climate chambers and
in buildings (Busch, 1992; Yang and Zhang, 2008).
The standard approach to comfort-based control in-
volves regulating the internal environment variables
to ensure a PMV value of zero (Shukor et al., 2007;
Yang and Su, 1997; Freire et al., 2008).
1.1.1 Predicted Mean Vote and its Alternative
Versions
Although PMV can be succesfully used in a design
phase (both for houses and buildings), it has some
drawbacks when used for HVAC controllers. Firstly,
it requires a substantial amount of environmentaldata.
For a controller in real-time this information is only
accessible via sensors. However some measurements,
such as air velocity, require costly sensors, while,
there are no sensors for variables such as clothing and
activity level. Secondly, PMV is a statistical measure
which assumes a large number of people experienc-
ing the same conditions. For small groups of peo-
ple within a single room or zone in a building, how-
ever, PMV may not be an accurate measure. (Ku-
mar and Mahdavi, 2001) analysed the discrepancy
between predicted mean vote proposed in (Fanger,
1972) and observed values based on a meta-analysis
of the field studies database made available under
ASHRAE RP-884 and finally proposing a framework
to adjust the value of thermal comfort indices (a
modified PMV). The large field studies on thermal
comfort described in (Humphreys and Nicol, 2002),
(de Dear and Schiller Brager, 2001) and (Humphreys
and Nicol, 2000), have shown that PMV does not give
correct predictions for all environments. (de Dear
and Schiller Brager, 2001) found PMV to be unbi-
ased when used to predict the preferred operativetem-
perature in the air conditioned buildings. PMV did,
however, overestimate the subjective warmth sensa-
tions of people in warm naturally ventilated buildings.
(Humphreys and Nicol, 2000) showed that PMV was
less closely correlated with the comfort votes than
were the air temperature or the mean radiant temper-
ature, and that the effects of errors in the measure-
ment of PMV were not negligible. Finally the work
in (Humphreys and Nicol, 2002) also showed that the
discrepancy between PMV and the mean comfort vote
was related to the mean temperature of the location.
In addition to the relative inaccuracy, the PMV model
is a nonlinear relation, and it requires iteratively com-
puting the root of a nonlinear equation, which may
take a long computation time. Therefore, a number
of authors have proposed alternative methods of cal-
culation to the main one proposed in (Fanger, 1972).
Fanger and (ISO, 1994) suggest using tables to de-
termine the PMV values of various combinations be-
tween the six thermal variables. (Sherman, 1985) pro-
posed a simplified model to estimate the PMV value
without any iteration step, by linearizing the radia-
tion exchange term in Fanger’s model. This study in-
dicated that the simplified model was only accurate
when the occupants are close to being comfortable.
(Federspiel and Asada, 1992) proposed a thermal sen-
sation index, which is a modified form of Fanger’s
model. They assumed that the radiative exchange and
the heat transfer coefficient are linear, and they also
assumed that the clothing insulation and heat gener-
ation rate of human activity are constant. They then
derived a thermal sensation index that is an explicit
function of the four environmental variables. How-
ever, as the authors said, the simplification of Fanger’s
PersonalizedThermalComfortForecastingforSmartBuildingsviaLocallyWeightedRegressionwithAdaptiveBandwidth
33

PMV model results in significant error when the as-
sumptions are not respected. On the other hand, in
(Bingxin et al., 2011) and (Atthajariyakul and Leep-
hakpreeda, 2005) different approaches have been pro-
posed in order to compute PMV avoiding the difficult
iterative calculation. The former proposes a Genetic
Algorithm Back Propagation neural network to learn
user comfort based both on historical data and real-
time environmental measurements. The latter pro-
poses a neural network applied to the iterative part of
the PMV model that, after a learning phase, based on
historical data, avoids the evaluation of such iterative
calculation in real-time.
1.1.2 Beyond the PMV
Recent trends in the study of thermal environment
conditions for human occupants are reported in the
recently accepted revisions to ASHRAE Standard
55, which includes a new adaptive comfort standard
(ACS). According to (de Dear and Brager, 2002) this
adaptive model could be an alternative (or a comple-
mentary) theory of thermal perception. The funda-
mental assumption of this alternative point of view
states that factors beyond fundamental physics and
physiology play an important role in building occu-
pants’ expectations and thermal preferences. PMV
does take into account the heat balance model with
environmental and personal factors, and is able to ac-
count for some degrees of behavioral adaptation such
as changing one’s clothing or adjusting local air ve-
locity.
However, it does not take into account the possi-
ble adaptation of an individual as a result from his/her
interaction with the environment (i.e. personal ther-
mal control), which, in turn, may alter his/her expec-
tations, and thus, their thermal sensation and satis-
faction. In particular, the level of comfort perceived
by each individual also depends on their degree of
adaptation to the context and to the environmental
changes, and therefore the specificity of each individ-
ual should be taken into account to learn and predict
comfort satisfaction.
For this reason, some authors have proposed tech-
niques based on learning the perception of comfort by
individuals. For example, in (Feldmeier and Paradiso,
2010) the author proposes a system able to learn in-
dividual thermal preferences using a Nearest Neigh-
bor Classifier, taking into account only four variables
(air temperature, humidity, clothing insulation and
human activity), acquired by means of wearable sen-
sors. In (Schumann et al., 2010), a Nearest Neighbor
Classification-like method was implemented in order
to learn individual user preferences based on histori-
cal data, using only one variable (air temperature). On
other hand in (Daum et al., 2011) the authors propose
a personalized measure of thermal comfort based on
logistic regression to convert user votes to a probabil-
ity of comfort.
In this study we consider such alternative and
more practical approaches to predicting thermal com-
fort through the automatic learning of the comfort
model of each user based on his/her historical records.
We apply the Robust Locally Weighted Regression
technique (Cleveland, 1979) with an Adaptive Band-
width (LRAB), one of the family of statistical pat-
tern recognition methods. Non-parametric regres-
sion methods, or kernel-based methods, are well es-
tablished methods in statistical pattern recognition
(Hastie et al., 2003). These methods do not need any
specific prior relation among data. Hence, there are
no parameter estimates in non-parametric regression.
Instead, to forecast, these methods retain the data
and search through them for past similar cases. This
strength makes non-parametric regression a powerful
method due to its flexible adaptation in a wide vari-
ety of situations. The Robust Locally Weighted Re-
gression is one of a number of nonparametric regres-
sions. It fits data by local polynomial regression and
joins them together. The first version of this method
was first introduced by Cleveland (Cleveland, 1979),
and it was further developed for multivariate models
in (Cleveland and Devlin, 1988).
2 KERNEL METHODS
In this section we describe a class of techniques used
throughout this paper, which achieve flexibility in es-
timating the regression function f (X) over domain
ℜ
p
by fitting a different but simple model separately
at each query point x in ℜ
p
. This is done by using
only those observations close to the target point x to
fit the simple model, and in such a way that the result-
ing estimated function
[
f(X) is smooth. This local-
ization is achieved by means of a weighting function
kernel K
λ
(x,x
i
), assigning a weight to x
i
based on its
distance from x. The kernels K
λ
are generally char-
acterized by a parameter λ that is related to the width
of the neighborhood (i.e. kernel bandwidth). In the
next section we first describe the Nadaraya-Watson
kernel-weighted average, then in 2.2 the Robust Lo-
cally Weighted Regression and, finally, in 2.3 the pro-
posed approach to select the kernel bandwidth λ.
2.1 Nadaraya-Watson Kernel Method
Let (x
i
,y
i
) denote a response, y
i
, to a recorded value
x
i
∈ ℜ
p
, for i = 1,. .., n. In this paper x
i
denotes the
SMARTGREENS2013-2ndInternationalConferenceonSmartGridsandGreenITSystems
34

environmental variables (inside air temperature, hu-
midity etc.) and the response y
i
represents the satis-
faction degree (real-valued from −3 to +3) that the
user has given in response to the condition x
i
, and
then stored in a database. The aim is to assess the
response ˆy =
d
f(x) (i.e. predict the degree of satisfac-
tion) for any new input value x. The approach aims to
estimate a local mean around x, giving all the points
in the neighborhood different weights. In particular,
we can assign weights that die off smoothly with dis-
tance to the target point. In the Nadaraya-Watson ker-
nel method (Bishop, 2006) the resulting estimated re-
sponse ˆy is:
d
f(x) =
∑
n
i=1
K
λ
(x,x
i
)y
i
∑
n
i=1
K
λ
(x,x
i
)
(1)
There are many kernel functions K
λ
proposed in
the literature. In this paper we used three different
kernel functions among the most used and which gen-
erally lead to satisfactory results.
2.1.1 Epanechnikov Quadratic Kernel
The Epanechnikov quadratic kernel is defined as fol-
low:
K
λ
(x,x
i
) = D
|x− x
i
|
λ
(2)
with
D(σ) =
(
3
4
(1− σ
2
) if |σ| ≤ 1,
0 otherwise.
The smoothing parameter λ, which determines the
width of the local neighborhood, has to be chosen.
Large λ implies lower variance (it takes into account
more observation points), but higher bias (it assumes
the true function is almost constant inside the win-
dow).
2.1.2 Tricube Kernel
The tricube kernel is another popular compact kernel.
It is still defined by Equation (2) but with:
D(σ) =
(
(1− |σ|
3
)
3
if |σ| ≤ 1,
0 otherwise.
This is flatter on the top than Epanechnikov kernel
and is differentiable at the boundary.
2.1.3 Gaussian Kernel
The Gaussian kernel is a popular non-compact kernel.
It consists in the Gaussian density function D(σ) =
ψ(σ), which is centered in the query point x, and with
the standard deviation playing the role of the window
size.
2.2 Robust Locally Weighted
Regression with Adaptive
Bandwidth
This method is based on the work in (Cleveland,
1979). In the following, we will only describe the
proposed LRAB method, while for a more general
description of the robust locally weighted regression,
the readers should refer to the work in (Cleveland,
1979). Before giving precise details on the LRAB
procedure, we attempt to explain the basic idea of
the method. Recall that (x
i
,y
i
) denotes a response,
y
i
, to a recorded value x
i
∈ ℜ
p
, for i = 1, ... ,n, stored
in a database.The aim is still to assess the response
ˆy =
d
f(x) for a new input value x. Let b(x) be a vec-
tor of polynomial terms of degree d. For example,
if we have a linear regression (d = 1) in two vari-
ables (p = 2), we have b(x) = (1,x
1
,x
2
), or if we a
quadratic regression (d = 2) in two variables (p = 2),
we have b(x) = (1,x
1
,x
2
1
,x
2
,x
2
2
), At each query point
x ∈ ℜ
p
, the aim is to solve:
min
β(x)
n
∑
i=1
K
λ
(x,x
i
)(y
i
− b(x
i
)
T
β(x))
2
(3)
to find the estimated function
d
f(x) = b(x)
T
ˆ
β(x). The
kernel will be a function such as those defined in sec-
tion 2.1. This procedure computes the initial fitted
values. Anyway, in the real-world, some recorded
values (x
i
,y
i
) could be affected by noise or be un-
reliable. The above procedure doesn’t itself elimi-
nate such values. The general idea to do this, is to
strengthen the above preliminary estimation, assign-
ing a different weight ψ
i
to each pairs (x
i
,y
i
) based
on the residual ( ˆy
i
− y
i
) (the larger the residual, the
smaller the associated weight). Then, the equation
(3) is computed replacing K
λ
with ψ
i
∗ K
λ
. This is
an iterative procedure. In this way, and generally af-
ter few iterations, the contribution of some eventually
noisy points to the regression is decreased. To achieve
this goal, let us define the bisquare function:
Γ(ξ) = (1− ξ
2
)
2
(4)
for |ξ| < 1; otherwise Γ(ξ) = 0. Then, for a fixed
new entry point x, let:
ρ
i
= ( ˆy
i
− y
i
) (5)
be the residuals for i = 1, ..., n, between the origi-
nal points y
i
and the estimated points ˆy
i
(i.e. by means
PersonalizedThermalComfortForecastingforSmartBuildingsviaLocallyWeightedRegressionwithAdaptiveBandwidth
35
5 10 15 20 25 30 35 40 45
−2
0
2
Inside air Temperature [Celsius]
User Votes [PMV scale]
0 10 20 30 40 50 60 70 80 90 100
−2
0
2
Relative Humidity [%]
User Votes [PMV scale]
0 5 10 15 20 25 30 35 40 45 50
−2
0
2
Mean Radiant Temperature [Celsius]
User Votes [PMV scale]
Figure 1: Subset of thermal perceived sensation (in PMV
scale) from users vs inside air temperature, humidity and
mean radiant temperature from database (ASHRAE, RP-
884).
of
ˆ
β(x)), and let m be the median of the |ρ
i
|. As de-
scribed in (Cleveland, 1979), we now choose robust-
ness weights by:
ψ
i
= Γ(ρ
i
/6m) (6)
At each step of the proposed procedure, the equa-
tion (6) is used to update the weight of the kernel
function in the equation (3) based on the residual ρ
i
.
In this way the value of the kernel function in (3) at
each recorded point x
i
, is decreased (increased) where
the residual value in x
i
(i.e. ψ
i
) is too high (too low),
so as to improve the regression for the next step.
2.2.1 Adaptive Bandwidth
In order to choose the bandwidth λ, we first needs
to take into account the fact that the density of the
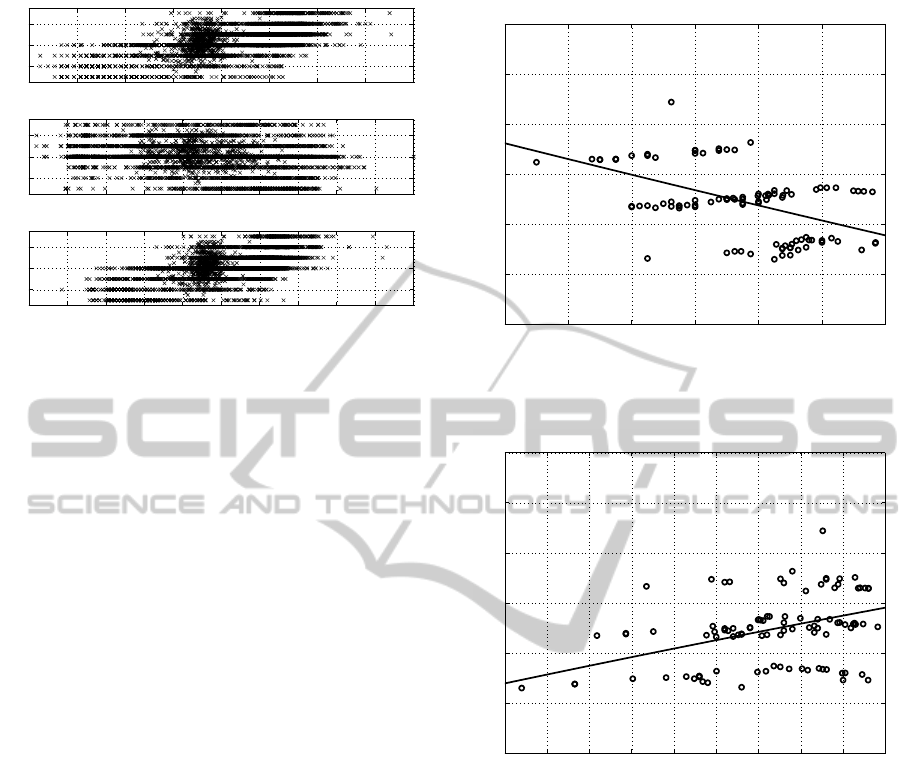
recorded data may be variable. Figure 1 shows a
global view of a subset of field data from a public
database (ASHRAE, RP-884), which were used for
our tests. In this figure, for all three graphs, it shows
the thermal perception from users (reported with the
PMV scale) in respect to three environmental vari-
ables, i.e. inside air temperature, humidity and mean
radiant temperature (MRT).
As shown in fig. 1, there are areas in which the
data are clustered closely together (in the center),
while, on other hand, other areas are characterised
by sparse data (on the boundaries). If in this situ-
ation we use a fixed value for the bandwidth λ, the
result is what is shown, as an example, in figures 3
and 4. In these figures, we report the residual (i.e. the
difference between the predicted vote and the actual
vote) computing a regression with p = 2 (using in-
side air temperature and humidity) for a random user
22 24 26 28 30 32 34
−3
−2
−1
0
1
2
3
Temperature [Celsius]
Residual
Fixed Bandwidth: Residual vs Inside Air Temperature
Figure 2: Residual vs inside air temperature, for an user
with 100 records from (ASHRAE, RP-884) using a regres-
sion in 2 variables with a fixed bandwidth λ for the kernel.
0 5 10 15 20 25 30 35 40 45
−3
−2
−1
0
1
2
3
Relative Humidity [%]
Residual
Fixed Bandwidth: Residual vs Humidity
Figure 3: Residual vs humidity, for an user with 100 records
from (ASHRAE, RP-884) using a regression in 2 variables
with a fixed bandwidth λ for the kernel.
with 100 votes stored. It easy to see that the residual
tends to vary with the values of the input variables,
and this is generally an undesired effect for any kind
of predicting technique. That effect occurs because,
using a fixed bandwidth there are less points support-
ing the regression where the data are sparse and, on
other hand, more supporting points where the data are
denser.
In view of this, it would be appropriate to have a
large smoothing parameter where the data are sparse,
and a smaller smoothing parameter where the data are
denser. In this situation an adaptive parameter has
been introduced. Let the ratio ν/n (where ν < n), de-
scribe the proportion of the sample which contributes
strictly positive weight to each local regression (for
example if the ratio is 0.7, it means that 70% of the
recorded data contributes to the regression). Once we
SMARTGREENS2013-2ndInternationalConferenceonSmartGridsandGreenITSystems
36

22 24 26 28 30 32 34
−3
−2
−1
0
1
2
3
Temperature [Celsius]
Residual
Adaptive Bandwidth: Residual vs Inside Air Temperature
Figure 4: Residual vs inside air temperature, for the user
in figures 2 and 3 using a regression in 2 variables with an
adaptive bandwidth λ for the kernel.
0 5 10 15 20 25 30 35 40 45
−3
−2
−1
0
1
2
3
Relative Humidity [%]
Residual
Adaptive Bandwidth: Residual vs Relative Humidity
Figure 5: Residual vs humidity, for the user in figures 2 and
3 using a regression in 2 variables with an adaptive band-
width λ for the kernel.
have chosen ν/n (that means we have chosen ν, as n
is fixed), we select the ν nearest neighbours from the
new entry point x. Then, the smoothing parameter λ
is denoted by the distance of the most distant neigh-
bour among the ν neighbours selected. It should be
noted that the entire procedure requires the choice of
a single parameter setting. This choice generally im-
proves the previous effect, giving rise to a results as
those shown in the figures 4 and 5, where the residual
is kept more constant for both input variables.
2.2.2 The Algorithm
The proposed method can be described by the follow-
ing sequence of operations (table 1): the algorithm
is initialized by setting only one parameter (step 1).
Then, for each new entry point x (step 2), it first com-
Table 1: Pseudocode for the proposed LRAB.
LRAB
1: Initialize: set parameters ν
2: For each entry point x:
2.1: minimise (3)
2.2: while iterations < max iterations do:
2.2.1: for each i compute (6)
2.2.2: minimise (3) replacing K
λ
with ψ
i
∗ K
λ
2.3: end while
3: end
putes an initial fitting (step 2.1), then it strengthens
the initial regression by the steps 2.2.1 to 2.2.2, per-
forming the sub-procedure described in the previous
section, iteratively. If we have M new entry points x
in total, the steps from 2.1 to 2.3 are repeated M times
(one time for each new entry point).
3 EXPERIMENTS
This section describes the experimental results ob-
tained from a comparison between the proposed
method and both the Nadaraya-Watson kernel method
and the PMV method. The three kernel functions de-
scribed in section 2.1 are used to compute and com-
pare LRAB and Nadaraya-Watson methods. It should
be noted that, although PMV is not based on a learn-
ing approach, in this paper, we compare our method
with PMV since the latter is the international standard
used to predict comfort in current building design and
operation (ISO, 1994).
In particular, LRAB has been compared with
the aforementioned methods on real data from the
ASHRAE RP-884 database. This collection contains
52 studies with more than 20,000 user comfort votes
from different climate zones. However, some of these
field studies contain only a few votes for each user.
Thus they are not well suited for testing the proposed
algorithm. This is because our approach seeks to learn
the user preferences based on their votes, and it re-
quires sufficiently many data records. For this reason,
only the users with more than 10 votes have been used
to compute the proposed LRAB. After removing the
studies and records as described above we were left
with 5 climate zones, 161 users and 6421 records.
LRAB has been implemented in Matlab
TM
, using
the trust-region method to minimize the problem in
(3), with a termination tolerance of 10
−6
. The exper-
iments have been performed through leave-one-out
PersonalizedThermalComfortForecastingforSmartBuildingsviaLocallyWeightedRegressionwithAdaptiveBandwidth
37

validation, for each user (i.e. using a single observa-
tion from the original sample as the validation data,
and the remaining observations as the training data).
The algorithms are evaluated considering the
difference |δV| between the computed votes (by
all methods) and the actual vote (reported in the
database). As with the field studies (Ari et al.,
2008),(Schumannet al., 2010), a prediction is defined
to be accurate if |δV| < 0.7.
The computation time depends on the number of
points have to be evaluated for each prediction; for
example, we’ve found that for predictions involving
100 records they take, on average, less than 5 seconds.
In the following tables 2, 3 and 4 are reported the
comparison (in terms of percentage of success) be-
tween LRAB, Nadaraya-Watson and PMV using re-
spectively one, two and three variables.
Table 2: Comparison between LRAB, Nadaraya-Watson
and PMV using only one variable for LRAB and Nadaraya-
Watson, giving percentage accuracies.
Temperature MRT Humidity
PMV 38.47
LRAB
Tricube 64.69 64.42 57.78
Epanechnikov 64.44 64.34 55.91
Gaussian 60.06 61.11 51.90
Nadaraya-Watson
Tricube 49.48 50.19 40.11
Epanechnikov 52.07 53.38 41.89
Gaussian 51.61 52.21 35.55
Tables 2, 3 and 4 illustrate how accurately the
LRAB predicts the actual comfort vote of each user
compared with Nadaraya-Watson and PMV. With
only one variable, LRAB achieves more than 64%
accuracy (using both tricube and Epanechnikov ker-
nels), while PMV only achieves 38% accuracy.
The other considered kernel method, the Nadaraya-
Watson method with 52 − 53% accuracy also im-
proves on the PMV method, but doesn’t match the
accuracy of the proposed LRAB method. Similarly
results are shown in Tables 3 and 4 for respectively
two and three variables. In particular, the best result is
achieved with three variables where LRAB achieves
69% accuracy with both tricube and Epanechnikov
kernels.
Moreover, one can argue that kernel methods, un-
like PMV, are essentially methods that learn from the
Table 3: Comparison between LRAB, Nadaraya-Watson
and PMV using two variables for LRAB and Nadaraya-
Watson, giving percentage accuracies.
Temp. and Hum. Temp. and MRT
PMV 38.47
LRAB
Tricube 66.70 67.03
Epanechnikov 65.91 65.84
Gaussian 65.70 65.14
Nadaraya-Watson
Tricube 39.81 50.87
Epanechnikov 41.12 50.22
Gaussian 38.22 49.81
Table 4: Comparison between LRAB, Nadaraya-Watson
and PMV using three variables for LRAB and Nadaraya-
Watson, giving percentage accuracies.
Temp., Hum and MRT
PMV 38.47
LRAB
Tricube 69.27
Epanechnikov 69.22
Gaussian 65.01
Nadaraya-Watson
Tricube 45.17
Epanechnikov 43.63
Gaussian 50.19
data, and so they require a sufficient amount of data
to give the best results. To test the influence of the
amount of data on the proposed LRAB, we’ve statisti-
cally investigated this effect on a subset of users from
the database (ASHRAE, RP-884). This subset in-
cludes 39 users, with at least 110 comfort votes from
each single user. We investigated the variation of the
percentage of success (according to the accuracy level
|δV| < 0.7) of the LRAB and Nadaraya-Watson using
three input variables, and the PMV, varying the num-
ber of samples used for the above methods in a range
from 10 to 110 samples. The results are shown in fig-
ure 6, showing that from 50 to 110 samples, the accu-
racy of the LRAB (80% in this case) remains roughly
constant. Hence, based on this investigation, we can
SMARTGREENS2013-2ndInternationalConferenceonSmartGridsandGreenITSystems
38

10 20 30 40 50 60 70 80 90 100 110
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Number of samples
Accuracy
Figure 6: Accuracy vs number of samples using 3 variables
for: LRAB (circle dots), Nadaraya-Watson (square dots)
and PMV (diamond dots).
conclude that the level of accuracy certainly is biased
by the amount of data used in the regression, but this
is true especially for a small amount of data, and the
results do not show much improvement after a certain
threshold. Finally, we can also see that LRAB over-
comes the Nadaraya - Watson method for almost the
entire tested range (from 20 up to 110 samples).
4 CONCLUSIONS
In the present paper, we have proposed the use of
robust locally weighted regression with an adaptive
bandwidth to predict individual thermal comfort. The
approach has been characterized and compared with
an other standard kernel method (i.e. the Nadaraya-
Watson method) and with the traditional PMV ap-
proach. The experiments were carried out using pub-
licly available datasets: they have shown that our
LRAB outperforms both Nadaraya-Watson and the
traditional PMV approaches in predicting thermal
comfort. We also investigated the influence of the
amount of the data used by LRAB on its performance,
concluding that the performance only degrades when
the predicted value is based on just a small number
of samples (less than 40 in this case). Since LRAB
can be computed quickly, and requires only a single
parameter setting that is easily obtained, then if in-
dividual comfort responses are available, this method
is feasible for use as a comfort measure in real time
control. The next step will the extension of the present
work to a similar and more challenging context: bal-
ancing the preferences of a number of different oc-
cupants sharing the same space in buildings (shared
offices)(Wilson, 2012).
This work is part of the Strategic Research Cluster
project ITOBO (supported by the Science Foundation
Ireland), for which we are acquiring occupantcomfort
reports and fine grained sensor data, and construct-
ing validated physical models of the building and its
HVAC systems. The intention is then to use the com-
fort reports and sensor data as input to our LRAB
method, and then to use the output of LRAB as the in-
put to intelligent control systems which optimise the
internal comfort for the specific individual occupants.
ACKNOWLEDGEMENTS
This work is supported by Intel Labs Europe
and IRCSET through the Enterprise Partnership
Scheme, and also in part by Science Foundation Ire-
land through SFI Research Cluster ITOBO (grant
No. 07.SRC.I1170), and grant No. 08/PI/I1912.
REFERENCES
Ari, S., Wilcoxen, P., Khalifa, H., Dannenhoffer, J., and
Isik, C. (2008). A practical approach to individual
thermal comfort and energy optimization problem. In
Fuzzy Information Processing Society, 2008. NAFIPS
2008. Annual Meeting of the North American, pages 1
–6.
ASHRAE (2010). ASHRAE Standard: Thermal Environ-
mental Conditions for Human Occupancy. ASHRAE.
Atthajariyakul, S. and Leephakpreeda, T. (2005). Neural
computing thermal comfort index for HVAC systems.
Bingxin, M., Jiong, S., and Yanchao, W. (2011). Ex-
perimental design and the GA-BP prediction of hu-
man thermal comfort index. In Natural Computation
(ICNC), 2011 Seventh International Conference on,
volume 2, pages 771 –775.
Bishop, C. M. (2006). Pattern Recognition and Machine
Learning.
Busch, J. F. (1992). A tale of two populations: thermal
comfort in air-conditioned and naturally ventilated of-
fices in Thailand. Energy and Buildings, 18(3-4):235
– 249.
Cleveland, W. S. (1979). Robust locally weighted regres-
sion and smoothing scatterplots. Journal of the Amer-
ican Statistical Association, 74(368):pp. 829–836.
Cleveland, W. S. and Devlin, S. J. (1988). Locally weighted
regression: An approach to regression analysis by lo-
cal fitting. Journal of the American Statistical Associ-
ation, 83(403):pp. 596–610.
Daum, D., Haldi, F., and Morel, N. (2011). A personal-
ized measure of thermal comfort for building controls.
Building and Environment, 46(1):3–11.
de Dear, R. and Schiller Brager, G. (2001). The adap-
tive model of thermal comfort and energy conserva-
tion in the built environment. International Journal of
Biometeorology, 45:100–108.
PersonalizedThermalComfortForecastingforSmartBuildingsviaLocallyWeightedRegressionwithAdaptiveBandwidth
39

de Dear, R. J. and Brager, G. S. (2002). Thermal comfort
in naturally ventilated buildings: revisions to ashrae
standard 55. Energy and Buildings, 34(6):549 – 561.
Fanger, P. (1972). Thermal comfort: analysis and appli-
cations in environmental engineering. McGraw-Hill,
New York.
Federspiel, C. C. and Asada, H. (1992). User-adaptable
comfort control for HVAC systems. In American Con-
trol Conference, 1992, pages 2312 –2319.
Feldmeier, M. and Paradiso, J. A. (2010). Personalized hvac
control system. In In Internet of Things 2010 Confer-
ence.
Freire, R. Z., Oliveira, G. H., and Mendes, N. (2008). Pre-
dictive controllers for thermal comfort optimization
and energy savings. Energy and Buildings, 40(7):1353
– 1365.
Gagge, A. P., Fobelets, A. P., and Berglund, L. G. (1986).
A standard predictive index of human response to the
thermal environment.
Hastie, T., Tibshirani, R., and Friedman, J. H. (2003). The
Elements of Statistical Learning. Springer, corrected
edition.
Humphreys, M. and Nicol, J. (2000). Effects of measure-
ment and formulation error on thermal comfort in-
dices in the ashrae database of field studies. ASHRAE
transactions, 106:493–502.
Humphreys, M. A. and Nicol, J. F. (2002). The valid-
ity of iso-pmv for predicting comfort votes in every-
day thermal environments. Energy and Buildings,
34(6):667 – 684.
ISO (1994). ISO 7730: Moderate Thermal Environments—
Determination of the PMV and PPD Indices and Spec-
ification of the Conditions for Thermal Comfort. ISO.
Kumar, S. and Mahdavi, A. (2001). Integrating thermal
comfort field data analysis in a case-based building
simulation environment. Building and Environment,
36(6):711 – 720.
Olesen, B. W. (2004). International standards for the indoor
environment. Indoor Air, 14:18–26.
Schumann, A., Wilson, N., and Burillo, M. (2010). Learn-
ing user preferences to maximise occupant comfort in
office buildings. In Proceedings of the 23rd interna-
tional conference on Industrial engineering and other
applications of applied intelligent systems - Volume
Part I, IEA/AIE’10, pages 681–690, Berlin, Heidel-
berg. Springer-Verlag.
Sherman, M. (1985). A simplified model of thermal com-
fort. Energy and Buildings, 8(1):37 – 50.
Shukor, S. A. A., Kohlhof, K., and Jamal, Z. A. Z.
(2007). Development of a pmv-based thermal com-
fort modelling. In Proceedings of the 18th IASTED
International Conference: modelling and simulation,
MOAS’07, pages 670–675, Anaheim, CA, USA.
ACTA Press.
Wilson, N. (2012). On balancing occupants’ comfort in
shared spaces. In Proc. 6th Multidisciplinary Work-
shop on Advances in Preference Handling (MPREF-
12).
Yang, K. and Su, C. (1997). An approach to building energy
savings using the PMV index. Building and Environ-
ment, 32(1):25 – 30.
Yang, W. and Zhang, G. (2008). Thermal comfort in nat-
urally ventilated and air-conditioned buildings in hu-
mid subtropical climate zone in china. International
Journal of Biometeorology, 52:385–398.
SMARTGREENS2013-2ndInternationalConferenceonSmartGridsandGreenITSystems
40
