Edges Detection from Aeromagnetic Data using the Wavelet

Transform

Sid-Ali Ouadfeul

and Leila Aliouane

Algerian Petroleum Institute, IAP, XYZ, Boumerdès, Algeria

LABOPHT

FHC, UMBB, Boumerdès, Algeria

Keywords: Aeromagnetic, Structural Boundaries, Delimitation, Wavelet Transform.

Abstract: The main goal of this paper is to use the 2D Directional Continuous Wavelet Transform (DCWT) for

structural boundaries delimitation from geomagnetic data. The proposed idea is based on the mapping of

maxima of the modulus of the 2D DCWT for each scale used in the DCWT calculation. Application to

synthetic data shows robustness of the technique. Application to the real geomagnetic data of In Ouzzal area

located in the West of Hoggar (Algeria) shows clearly the strength of this last. Comparison with the analytic

signal solutions exhibits that the DCWT is able to predict a pattern of boundary that is hidden by the noise

in the analytic signal and eliminated by a threshold. The proposed method proves to be more powerful easy

to use and versatile where classical methods of potential field interpretation fail or are very constraining.

1 INTRODUCTION

The continuous wavelet transform has becoming a

very useful tool in geophysics (Ouadeul, 2006);

(Ouadfeul, 2007). In Potential field analysis it was

used to locate causative sources point in 2D in

combination with the analytic signal (Ouadfeul and

Aliouane, 2011).

Ouadfeul and Alioaune (2012) have published a

paper on the characterization of geological

boundaries using 2D wavelet transform of gravity

data, the proposed technique has been applied on the

Hoggar.

Ouadfeul et al., (2012) have proposed a new

technique of structural boundaries delimitation from

aeromagnetic data using the 2D ditrectional

continuous wavelet transform, obtained results show

robustness of the proposed technique.

Here we propose a technique of boundaries

delimitation from aeromagnetic data using the 2D

continuous wavelet transform, we start the paper by

describing the relation between the wavelet

transform and the upward continuation, after that we

apply the proposed idea to a synthetic and real data

of an area located in the Algerian Sahara. We

finalize the paper by a results interpretation and a

conclusion.

2 THE CONTINUOUS WAVELET

TRANSFROM AND

POTENTIAL FILED DATA

The sharp contrasts that show the potential data are

assumed to result from discontinuities or interfaces

such as faults, flexures, contrasts intrusive rocks ...

For contacts analysis between geological structures,

we use usually the classical methods based on the

location of local maxima of the modulus of the total

(Nabighian, 1984) or the horizontal gradient

(Blakely et al., 1986), or the Euler’s deconvolution

(Reid et al., 1990). This technique allows, in

addition to localization in the horizontal plane of

contact, an estimate of their depth. The potential

field reduced to the pole, over a vertical contact,

involving the presence of rocks of different

susceptibilities is indicated by a low in side rocks of

low susceptibility and a high in side rocks of high

susceptibility. The inflection point is found directly

below the vertical contact. We can use this

characteristic of geomagnetic anomalous for

localization of abrupt susceptibility change. If the

contact has a dip, the maxima of horizontal gradients

move in the direction of dip. To determine the dip

direction of contacts, we upward the map of the

potential field at different altitudes. At each level,

the maxima of horizontal gradient are located. If the

697

Ouadfeul S. and Aliouane L..

Edges Detection from Aeromagnetic Data using the Wavelet Transform.

DOI: 10.5220/0004380506970701

In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods (PRG-2013), pages 697-701

ISBN: 978-989-8565-41-9

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

structures are vertical, all maxima are superposed.

However, moving of maxima with the upward

indicates the direction of the dip. The potential

theory lends perfectly to a multiscale analysis by

wavelet transform.

By choosing an appropriate wavelet,

measurement of geomagnetic field or its spatial

derivatives can be processed as a wavelet transform.

Indeed, this analysis unifies various classical

techniques: it process gradients that have been

upward to a range of altitudes. The expressions of

various conventional operations on the potential

field are well-designed in the wavelet domain. The

most important is the equivalence between the

concept of scaling and the upward. Indeed, the

wavelet transform of a potential field F

(x, y) at a

certain scale a = Z/Z

can be obtained from

measurements made on the level Z

by:

1. Upward continue the measured field a level

Z=a*Z

2. Calculation of the horizontal gradient in x and y

directions.

3. Multiplication by a.

For a multiscale analysis of contacts, it is sufficient

to look for local maxima of the modulus of the

continuous wavelet transform (CWT) for different

scales to get exact information about geological

boundaries (Ouadfeul et al., 2010).

3 APPLICATION TO SYNTHETIC

DATA

The proposed idea has been applied at a synthetic

model of a cylinder and prism, parameters of these

last are resumed in tables 01 and 02. Figure 1 is the

magnetic response of this model generated with a

grid of dimensions 100mx100m. The first operation

is to calculate the modulus of the continuous wavelet

transform. The analyzing wavelet is the Poisson

Kernel defined by equation below (Ouadfeul et al.,

2012).





2/3







yxP

The choice of the analyzing wavelet is based on the

analogy between the upward continuation and the

continuous wavelet transform, if the analyzing

wavelet is the Poisson’s Kerenel, the Modulus of the

continuous wavelet transform at a scale a is

equivalent to the upaward continuation of this field

at the same scale( Ouadfeul et al, 2010). Calculation

of maxima of the continuous wavelet transform of

the geomagnetic field reduced to the pole at the scale

a is equivalent to maxima of the horizontal gradient

of this filed upwarded to Z=a (Ouadfeul et al.,

2010).

Scales are varying following a power law:

djj

2* j=0,1,……,N

)()(*2 YXa 



is the grid dimension following the x

dimension.



is the grid dimension following the y

dimension.

max max

(* )(* )

log( ) / log(2)

XN YM





d is a real number, in this case we take

3.0

max

=100

max

=100

Figure 2 shows this modulus plotted at the smaller

scale a=282m. The second step consists to calculate

its maxima, figure 3 is a map of these maxima for

the full range of scales (Scales varied from 282m to

1131m). Solid curves are the exact boundaries of the

prism and the cylinder. One can remark that the

maxima of the continuous wavelet transform are

positioned around the two exact boundaries.

Table 1: Physical parameters of the Cylinder.

Coordinates of the center (5000, 2500, -250).

Ray 1500m.

High 2500m.

Magnetic Susceptibility K=0.015 SI.

F 37000 nT

Declination D=0°

Inclination I=90°

Table 2: Physical parameters of the Prisme.

Coordinates of the center (5000, 7000, -300).

Width 3000m

Length 3000m.

High 2000m.

Magnetic Susceptibility K=0.01 SI.

F 37000 nT

Declination D=0°

Inclination I=90°

4 APPLICATION TO REAL DATA

The proposed idea is applied to the aeromagnetic

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

698

data of In Ouzzal, it is located in Hoggar. We start

by describing geology of massif of the area.

F(nT)

X(m)

Y(m)

Figure 1: Magnetic anomaly map of the synthetic model.

X(m)

Y(m)

C(X,Y)

Figure 2: Modulus of the 2D CWT at the smaller scale

a=282m.

Figure 3: Structural boundaries delimited by the 2D CWT.

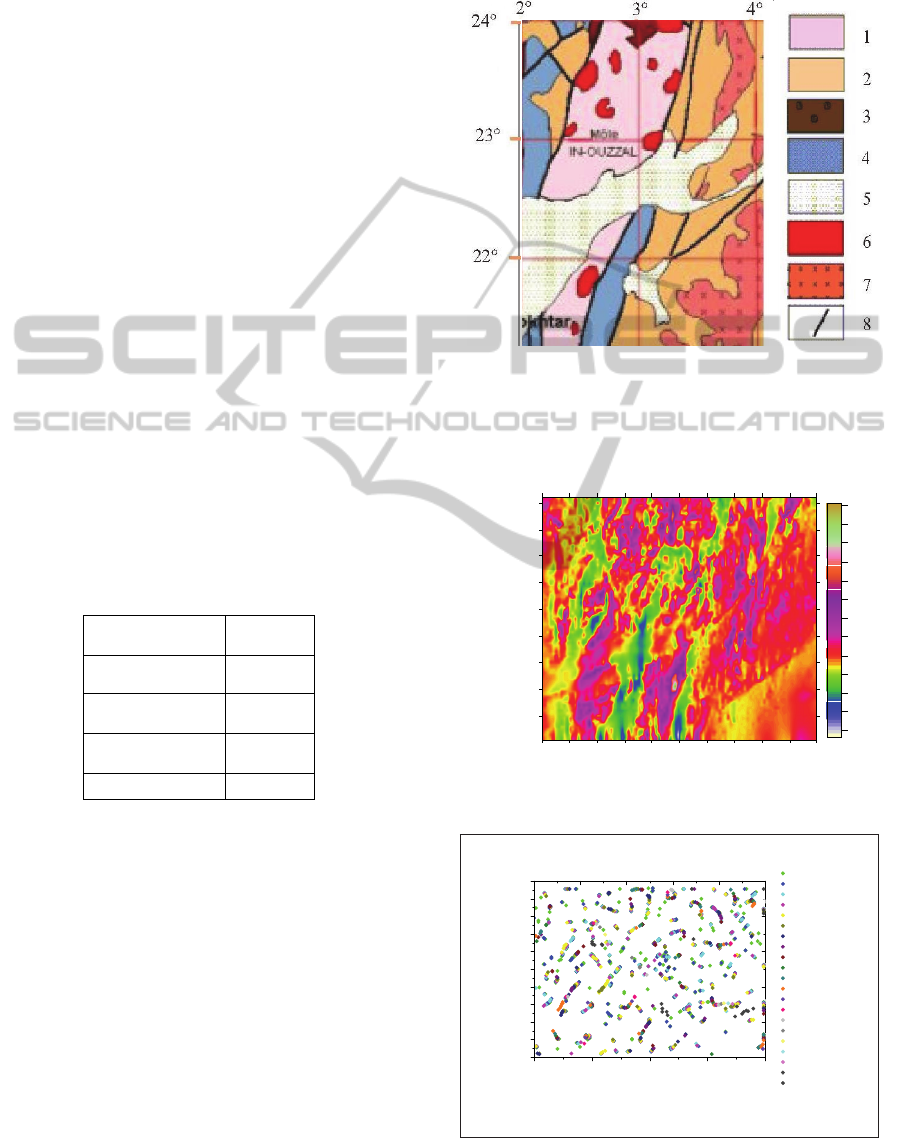
4.1 Geological Setting of in Ouzzal

The In Ouzzal terrane (Western Hoggar) is an

example of Archaean crust remobilized by a very-

high-temperature metamorphism during the

Paleoproterozoic (2 Ga). Structural geometry of the

In Ouzzal terrane is characterized by closed

structures trending NE-SW to ENE-WSW(figure 04)

that correspond to domes of charnockitic

orthogneiss. The supracrustal series are made up of

metasediments and basic-ultrabasic rocks that

occupy the basins located between these domes. In

In Ouzzal area, the supracrustal synforms and

orthogneiss domes exhibit linear corridors near their

contacts corresponding to shear zones. The structural

features in In Ouzzal area, observed at the level of

the base of the crust, argue in favour of a

deformation taking place entirely under granulite-

facies conditions during the Paleoproterozoic. These

features are compatible with D

homogeneous

horizontal shortening of overall NW-SE trend that

accentuates the vertical stretching and flattening of

old structures in the form of basins and domes. This

shortening was accommodated by horizontal

displacements along transpressive shear corridors.

During the Pan-African event, the brittle

deformation affected the granulites which were

retrogressed amphibolite and greenschists facies

(with the development of tremolite and chlorite, in

the presence of fluids along shear zones corridors.

Brittle deformations were concentrated in the

southern boundary of In Ouzzal. An important NW-

SE-trending dextral strike-slip pattern has been

mapped along which we can see the Eburnean

foliation F1 overprinted. This period was also

marked by ductile to brittle deformation along the

eastern shear zone bordering the In Ouzzal terrane

with steep fracture cleavage (NNW-SSE) and

conjugate joint pattern. All these structural features

are compatible with an ENE-WSW shortening in

relation with the collision between the West African

Craton and the Hoggar during the Pan-African

orogeny (Djemai et al., 2009).

4.2 Data Processing

In this section we have analyzed the aeromagnetic

data of In Ouzzal to demonstrate the power of the

2D CWT method to identify geological contacts.

Source codes in C language are developed to

calculate the 2D continuous wavelet transform and

the spatial distribution of its maxima at different

scales.

The geomagnetic field data are processed with a

regular grid of 750mX750m.

Figure 5 is the map of the anomaly magnetic

field



after reduction to the pole. Parameters of

reduction to the pole (RTP) are illustrated in table

03. After RTP the maximum of the anomaly

magnetic field will be found at the vertical of the

physical structures. The data are then filtered to

remove high frequency noise using a low pass

Butterworth filter with cut-off frequency of 0.29

cycles by km. The next step consists to calculate the

EdgesDetectionfromAeromagneticDatausingtheWaveletTransform

699

2D continuous wavelet transform of the filtered data.

The analyzing wavelet is the Poisson’s Kernel.

Parameters of scales calculation are:

=0.3, N

max

=255, M

max

=268.

The next operation consists to calculate maxima of

the modulus of the continuous wavelet transform for

each scale (scales varied between 2.12 and 9.09 km).

Figure 6 shows the chains of maxima in the X, Y,

log-scales coordinates. They are called the Skeleton

of the modulus of the wavelet transform. At each

scale we map points of maxima in the plan. The

obtained set of maxima for all ranged scales will

give the geometry of geologic contacts (Figure 7).

4.3 Results Interpretation and

Conclusions

The obtained contacts by CWT are compared with

the geological map. Obtained results show that the

proposed technique is able to identify contacts that

exist in the structural geology map.

We have proposed a technique of boundaries

identification based on the 2D directional continuous

wavelet transform. Firstly we have applied this idea

to a synthetic model, obtained results shows

robustness of CWT. Application on noised model

shows that CWT is sensitive to noise.

Table 3: Parameters of Reduction to the pole.

Longitude 3°

Latitude 22.5°

Elevation 1000m

Inclinaton 27.6

Declination -4.38

We have applied this technique to the

aeromagnetic data of In Ouzzal. Obtained results are

compared with the geological map and the analytic

signal solutions. One can remark that the 2D

continuous wavelet transform is able to detect

boundaries defined by geologists. Comparison with

analytic signal shows that the CWT is able to

identify contacts that not exist in the map of contacts

defined by AS. The results of this study show that

the proposed technique of edge detection based on

the wavelet transform is very efficient for geological

contacts analysis from maps of geomagnetic

anomalies. Indeed, this kind of analysis of potential

field maps can enhance conventional structural

studies. The identified geological structures have a

big importance in hydrogeological exploration,

mining and in the study of earthquakes and

landslides.

1-Archaean granulites; 2- Gneiss and metasediments; 3- Gneiss

with facies amphibole; 4- Indif gneiss; 5- Paleozoic curvature; 6-

Panafrican granite; 7-Volcano-sediments of Tafassasset; 8- Major

faults.

Figure 4: Structural boundaries of in Ouzzal.

4 0000 0 4 4 0000 48 00 00 5 20 000 5 60 0 00 60 00 00

2420000

2440000

2460000

2480000

2500000

2520000

2540000

2560000

2580000

-800

-600

-400

-200

200

400

600

800

1000

1200

1400

1600

X(m)

Y(m)

Figure 5: Magnetic anomaly map reduced to the pole.

400000 450000 500000 550000 600000

2400000

2420000

2440000

2460000

2480000

2500000

2520000

2540000

2560000

2580000

2600000

Y(m)

X(m)

a=3215.32m

a=3958.52m

a=4873.51m

a=6000.00m

a=7386.86m

a=9094.29m

a=11196.39m

a=13784.38m

a=16970.56m

a=20893.21m

a=25722.56m

a=31668.19m

a=38988.11m

a=48000.00m

a=59094.93m

a=72754.40m

a=89571.17m

a=110275.05m

a=135764.51m

a=167145.73m

a=205780.54m



Figure 6: Mapped contacts by the 2D CWT.

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

700

REFERENCES

Blakely, R. J. and Simpson, R. W, 1986. Approximating

edges of source bodies from magnetic or gravity

anomalies, Geophysics: 51, 1494–1498.

Caby. R, Bertrand. J. M. L, and Black. R, 1981. Pan-

African closure and ontinental collision in the Hoggar-

Iforas segment, central Sahara. in Kroner A (ed)

Precambrian Plate Tectonics, Elsevier, Amst. 407-

434.

Djemaï, S., Haddoum, H., Ouzegane. K., And Kienast, J-

R., 2009. Archaean Series Reworked At Proterozoic In

Amesmessa (West Hoggar): Cartography, Tectonic

Evolution And P-T Path, Bulletin du Service

Géologique National, Vol. 20, n°1, pp. 3 – 29.

Nabighian, M. N., 1984. Toward a three-dimensional

automatic interpretation of potential field data via

generalized Hilbert transforms: Fundamental relations:

Geophysics, 49, 957–966.

Ouadfeul, S., 2006: Automatic lithofacies segmentation

using the wavelet transform modulus maxima lines

WTMM combined with the detrended fluctuations

analysis DFA, 17 International Geophysical congress

and exhibition of Turkey.

Ouadfeul, S.., 2007, Very fines layers delimitation using

the wavelet transform modulus maxima lines WTMM

combined with the discrete wavelet transform DWT,

Presented in SEG Summer research workshop,

Antalya , Turkey.

Ouadfeul, S and Aliouane. L, 2011, Mutiscale analysis of

3D analytic signal using the 2D continuous wavelet

transform, EAGE 6th Congress of Balkan Geophysical

Society - Budapest, Hungary.

Ouadfeul, S., Aliouane, L., Eladj, S., 2010, Multiscale

analysis of gomagnetic data using the continuous

wavelet transform, SEG expanded abstract; Vol29,

doi:10.1190/1.3513065.

Ouadfeul, S., Hamoudi, M., Aliouane, L., and Eladj, S.,

2012, Aeromagnetic data analysis using the 2D

directional continuous wavelet transform (DCWT),

Arab Journal of geosciences.

Ouadfeul, S., Aliouane, L., 2012, Multiscale analysis of

gravity data using the 2D directional continuous

wavelet transform. SEG Istanbul.

Reid, A. B., Allsop, J. M., Granser, H., Millett, A. J.,

Somerton, I. W., 1990. Magnetic interpretation in

three dimensions using Euler deconvolution:

Geophysics, 55, 80–91.

EdgesDetectionfromAeromagneticDatausingtheWaveletTransform

701