Lithofacies Prediction from Well Logs Data using Different Neural

Network Models

Leila Aliouane

, Sid-Ali Ouadfeul

, Noureddine Djarfour

and Amar Boudella

LABOPHYT,

Faculty of Hydrocarbone and Chemestry, University M’hamed Bougara, Boumerdès, Algeria

Algerian Petroleum Institue, IAP, Boumerdès, Algeria

FSTGAT-USTHB, Algiers, Algeria

Keywords: Lithofacies, Classification, MLP, RBF, SOM, Clayey Reservoir, Well-Logs.

Abstract: The main objective of this work is to predict lithofacies from well-logs data using different artificial neural

network (ANN) models. The proposed technique is based on three classifiers types of ANN which are the

self-organizing map (SOM), multilayer Perceptron (MLP) and radial basis function (RBF). The data set as

an input of the neural network machines are the eight borehole measurements which are the total natural

gamma ray; the three concentrations of the radioactive elements Thorium, Potassium and Uranium; the

slowness of the P wave, the bulk density, the neutron porosity and the photoelectric absorption coefficient

of two boreholes located in Algerian Sahara. Hence, the outputs of three neuronal kinds are the different

lithological classes of clayey reservoir. These classes are obtained by supervised and unsupervised learning.

The output results compared with basic stratigraphy show that the Kohonen map gives the best lithofacies

classification where the thin beds intercalated in the reservoir, are identified.

Consequently, the neural network technique is a powerful method which provides an automatic

classification of the lithofacies reservoir.

1 INTRODUCTION

Recently, pattern recognition context became a

popular interest in geosciences by neural network

techniques. In petrophysics, these last can be used

for classification (Aliouane et al., 2011); (Ouadfeul

and Aliouane, 2012) and approximation (Lim,

2005); (Amenian, 2005) and (Aminzadah, 1999);

(Aliouane et al., 2012) in reservoir characterization

by well log-data where the lithofacies prediction is

an important step in crossed formations, mainly, in a

reservoir.

Neural network as a nonlinear and non-

parametric tool is becoming increasingly popular in

well log analysis. Neural network is a computer

model that attempts to mimic simple biological

learning processes and simulate specific functions of

human nervous system. The main objective of this

work is to predict lithofacies from well-logs data

using different artificial neural network (ANN)

models. The proposed technique is based on three

classifiers types of ANN which are the self-

organizing map (SOM), multilayer Perceptron

(MLP) and radial basis function (RBF) in order to

choose the best lithological classifier.

The well-logs of the clayey reservoirs of two

boreholes located in Algerian Sahara are exploited.

One of them is selected as pilot well for training

networks and the second is used for generalization.

In the present study, we start by basic concepts

of principles of different neural network models

such as SOM, MLP and RBF and their training

model. Different learning parameters will be

discussed to improve the network’s architectures. At

the end, the results will be compared to a basic

stratigraphy.

2 DATA ANALYSIS OF THE

CLAYEY RESERVOIR

The clayey reservoirs are, generally, radioactive.

Their radioactivity is due to the presence of the three

nuclear elements such as Thorium, Potassium and

Uranium. The Cambrian reservoirs of two boreholes

located in Algerian Sahara present the geological

model constituted by sandstone and clay

(Shonatrach and Shlumberger, 2007). Thus, this kind

702

Aliouane L., Ouadfeul S., Djarfour N. and Boudella A..

Lithofacies Prediction from Well Logs Data using Different Neural Network Models.

DOI: 10.5220/0004380707020706

In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods (PRG-2013), pages 702-706

ISBN: 978-989-8565-41-9

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

of reservoir is easily identified by the total natural

gamma ray and its radioactive elements spectra

(Ellis and Singer, 2008). This analysis is confirmed

using other petrophysical parameters recordings

sensitive to clays. These are the slowness of the P

wave, the bulk density, the neutron porosity and the

photoelectric absorption coefficient. (figure 1 and 2).

Figure 1: Petrophysical parameters recordings of well-1.

Figure 2: Petrophysical parameters recordings of a well-2.

The data set as an input of the neural network

machines are the eight borehole measurements

which are the total natural gamma ray; the three

concentrations of the radioactive elements Thorium,

Potassium and Uranium; the slowness of the P wave,

the bulk density, the neutron porosity and the

photoelectric absorption coefficient of two boreholes

located in Algerian Sahara. Hence, the outputs of

three neuronal kinds are the different lithological

classes of clayey reservoir. These classes are

obtained by supervised and unsupervised learning

and constituted by 04 classes: sandstone, clay,

clayey sandstone and sandy clay (Figure 3).

Classe1

Classe 2 

Classe4

Classe3

Sandstone

Clayeysand

Clay

Sandyclay



Figure 3: Lithological classes of the clayey reservoir.

Data of well-1 are exploited for training and the

data of well-2 are used for generalization.

3 SELF ORGANIZING MAP

Self-organizing maps are different than other

artificial neural networks in the sense that they use a

neighborhood function to preserve the topological

properties of the input space (figure 4).

Figure 4: Kohonen’s map principle.

This makes SOM useful for visualizing low-

dimensional views of high-dimensional data, similar

to multidimensional scaling. The model was first

described as an artificial neural network by the

Finnish professor Teuvo Kohonen (Kohonen, 1982),

and is sometimes called a Kohonen map. Like most

LithofaciesPredictionfromWellLogsDatausingDifferentNeuralNetworkModels

703

artificial neural networks, SOMs operate in two

modes: training and mapping. Training builds the

map using input examples. It is a competitive

process, also called vector quantization. Mapping

automatically classifies a new input vector.

The goal of learning in the self-organizing map is

to cause different parts of the network to respond

similarly to certain input patterns. This is partly

motivated by how visual, auditory or other sensory

information is handled in separate parts of the

cerebral cortex in the human brain (Kohonen, 1982;

2000).

The training utilizes competitive learning. When

a training example is fed to the network, its

Euclidean distance to all weight vectors is

computed. The neuron with weight vector most

similar to the input is called the best matching unit

(BMU). The weights of the BMU and neurons close

to it in the SOM lattice are adjusted towards the

input vector. The magnitude of the change decreases

with time and with distance from the BMU. The

update formula for a neuron with weight vector

Wv(t) is:

Wv(t + 1) = Wv(t) + Θ (v, t)*α(t)*(D(t) - Wv(t))

where α(t) is a monotonically decreasing learning

coefficient and D(t) is the input vector. The

neighborhood function Θ (v, t) depends on the lattice

distance between the BMU and neuron v. In the

simplest form it is one for all neurons close enough

to BMU and zero for others, but a gaussian function

is a common choice, too. Regardless of the

functional form, the neighborhood function shrinks

with time. At the beginning when the neighborhood

is broad, the self-organizing takes place on the

global scale. When the neighborhood has shrunk to

just a couple of neurons the weights are converging

to local estimates.

This process is repeated for each input vector for

a (usually large) number of cycles λ. The network

winds up associating output nodes with groups or

patterns in the input data set. If these patterns can be

named, the names can be attached to the associated

nodes in the trained net.

During mapping, there will be one single

winning neuron: the neuron whose weight vector lies

closest to the input vector. This can be simply

determined by calculating the Euclidean distance

between input vector and weight vector.

While representing input data as vectors has been

emphasized in this article, it should be noted that

any kind of object which can be represented digitally

and which has an appropriate distance measure

associated with it and in which the necessary

operations for training are possible can be used to

construct a self-organizing map. This includes

matrices, continuous functions or even other self-

organizing maps.

The obtained lithofacies classification is

presented in figure 7b.

4 MULTILAYER PERCEPTRON

The employed Neural Network type is a standard

layered Neural Network type with a linear

accumulation and a sigmoid transfer function, called

multi-layer perceptron. Usually the network consists

of an input layer, receiving the measurement vector

x, a hidden layer and an output layer of units

(neurons). In this configuration each unit of the

hidden layer realizes a hyperplane dividing the input

space into two semi-spaces. By combining such

semispaces the units of the output layer are able to

construct any polygonal partition of the input space.

For that reason it is theoretically possible to design

for each (consistent) fixed sample a correct Neural

Network classifier by constructing a sufficiently fine

partition of the input space. This may necessitate a

large number of neurons in the hidden layer. The

model parameters consist of the weights connecting

two units of successive layers. In the training phase

the sample is used to evaluate an error measure and

a gradient descent algorithm can be employed to

minimize this net error. The problem of getting stuck

in local minima is called training problem.

The structure is constituted of one layer for

inputs, one hidden layer and one layer for outputs

(figure 5).

Figure 5: Architecture of MLP network.

Obtained lithological classification by the MLP

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

704

is presented in figure 7c.

5 RADIAL BASIS FUNCTION

Powell (1985) surveyed the early work on RBF

neural networks, which presently is one of the main

fields of research in numerical analysis. With respect

to this network, learning is equivalent to finding a

surface in a multidimensional space that provides a

best fit to the Learning data. Correspondingly,

generalization is equivalent to the use of this

multidimensional surface to interpolate the test data.

The construction of a RBF network in its most basic

form involves three entirely different layers. The

input layer is made up of input nodes. The second

layer is a hidden layer of high enough dimensions,

which serves a different purpose from that in the

multilayer perceptron. The output layer supplies the

response of the network to the activation patterns

applied to the input layer. In contrast to the

multilayer perceptron, the transformation from the

input space to the hidden layer space is non-linear,

whereas the transformation from the hidden layer

space to the output space is linear (figure 6).



f









Vecteurd’entrée

Vecteurdesortie

y

Matricedespoids

Fonctiond’activation

Couchecachée

Fonctiongaussienne





jj,σc



Figure 6: RBF principle.

The neurone number of the input layer is the

same for the RBF and for the MLP, corresponding to

the eight petrophysical measurements. The Obtained

lithological classification by the RBF is presented in

figure 7d.

6 RESULTS DISCUSSION AND

CONCLUSIONS

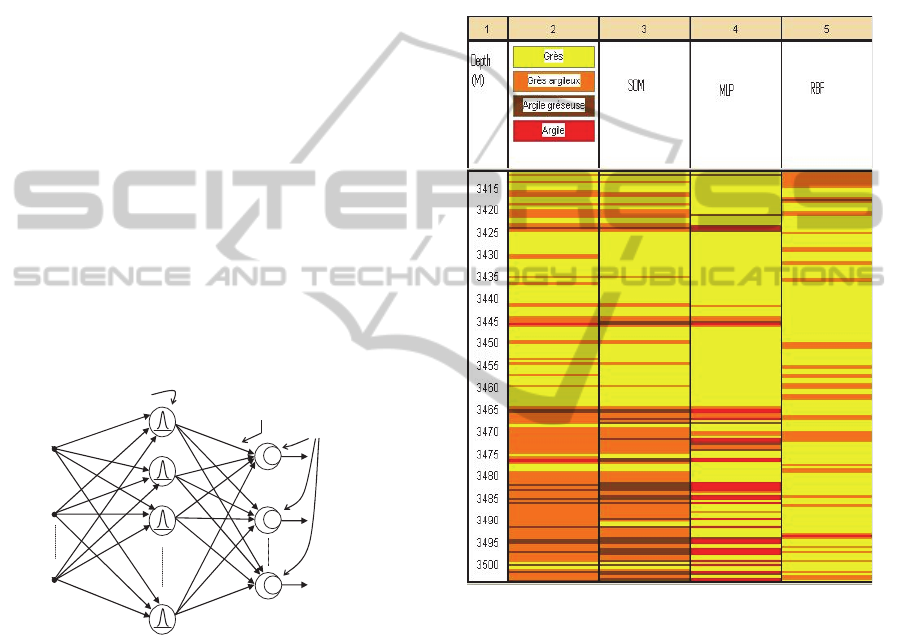
By analyzing figure 7, one can remark that the Self

Organizing neural network machine (figure 7b)

gives more lithological details than the MLP (figure

07c) and RBF (figure 7d) networks.

By implementing our analysis, we have

demonstrated that it is possible to provide an

accurate geological interpretation within a short time

in order to take immediate drilling and completion

decisions, but also, in a longer-term purpose, to

update the reservoir model.

Reservoir model based on the self organizing

map neural network machine with the raw data as

input gives a detailed information.

(a) (b) (c) (d)

Figure 7: Lithofacies classification of a reservoir of Well-

2. (a) basic stratigraphy; (b) by SOM; (c) by MLP; (d) by

RBF.

REFERENCES

Aliouane. L, Ouadfeul.S and Boudella. A, 2011, Fractal

analysis based on the continuous wavelet transform

and lithofacies classification from well-logs data using

the self-organizing map neural network. Arab J

Geosci, DOI 10.1007/s12517-011-0459-4.

Aliouane L., Ouadfeul S., Djarfour N., Boudella A., 2012.

Petrophysical parameters estimation from well-logs

data using Multilayer Perceptron and Radial Basis

Function neural networks. T. Huang et al (Eds):

ICONIP 2012, PartV, LNCS 7667, pp. 730-736,

Springer-Verlag.

LithofaciesPredictionfromWellLogsDatausingDifferentNeuralNetworkModels

705

Aminian. K, Ameri.S, 2005, Application of artificial

neural networks for reservoir characterization with

limited data, Journal of Petroleum Science and

Engineering 49 (2005) 212– 222.

Aminzadeh. F, Barhen . J, Glover. C. W and Toomarian.

N. B, 1999, Estimation of reservoir parameter using a

hybrid neural network, Journal of Petroleum Science

and Engineering 24 _1999. 49–56

Ellis D., V., Singer J. M., 2008. Well logging for earth

scientists. 2

edition, Spriger.

Kohonen T., 1982. Organization and associative memory.

Springer Series in information sciences, Vol. 8,

Springer-Verlag.

Kohonen T., 2000. Self-organizing map. Third edition,

Springer.

Lim S., L., 2005: Reservoir properties determination using

fuzzy logic and neural networks from welldata in

offshore Korea, Journal of Petroleum Science and

Engineering 49 (2005) 182– 192.

Ellis D. V., Singer J. M., 2008. Well logging for earth

scientists. 2

edition, Spriger.

Ouadfeul S., Aliouane L., 2012. Lithofacies classification

using Multilayer perecptron and the Self Organizing

neural network. T. Huang et al. (Eds.): ICONIP 2012,

Part V, LNCS 7667, pp. 737–744. Springer-Verlag.

Powell, M. J. D., 1985. Radial Basis Functions for

Multivariable Interpolation: A Review in IMA

Conference on Algorithms for the Approximation of

Functions and Data. RMCS, Shirvenham, UK, pp.

143–167.

Sonatrach and Shlumberger, 2007. Well Evaluation

Conference, Algeria.

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

706