Building an Intelligent Tutoring System for Chess Endgames

Matej Guid, Martin Mo

zina, Ciril Bohak, Aleksander Sadikov and Ivan Bratko

Faculty of Computer and Information Science, University of Ljubljana, Tr

ska cesta 25, Ljubljana, Slovenia

Keywords:

Intelligent Tutoring Systems, Artiﬁcial Intelligence, Education, Problem Solving, Chess Endgames, Chess.

Abstract:

We present the development of an intelligent tutoring system for chess endgames, and explain in detail the

system’s architecture that is comprised of ﬁve essential components. The rule-based domain model contains

a conceptualized domain theory, which serves as a bridge between the basic declarative domain theory and

procedural knowledge for concrete problem solving. The search engine is used to generate new chess problems

and to validate students’ solutions on the ﬂy. The tutoring model represents pedagogical knowledge and

follows the standard model-tracing approach. The student model contains the knowledge about the user in the

form of a skill meter, aiming to show the level of a student’s understanding of particular skills. Finally, the

user interface is where the interaction between a student and the tutor takes place.

1 INTRODUCTION

Several studies have demonstrated beneﬁts of chess

in education. Namely, the ﬁndings showed that chess

can lead to signiﬁcant progress in problem solv-

ing, memory enhancement, focusing, scoring of IQ

tests, creativity, critical thinking, visualizing, recog-

nizing patterns, and enhancing meta-cognitive skills

(Kazemi et al., 2012). Developing a successful intelli-

gent tutoring system (ITS) for chess endgames would

therefore have a signiﬁcant practical value.

While our primary goal is to develop an efﬁcient

intelligent tutoring system that leads to robust learn-

ing, we deem the secondary goal to be equally im-

portant: to obtain a formative evaluation of our meth-

ods to support automated conceptualization of learn-

ing domains (Mo

zina et al., 2012). The purpose of

these methods is to partially automate the process of

developing ITSs and thus considerably decrease the

high costs of building them.

In the present paper, we present the development

of the ITS for chess endgames. We describe in detail

the architecture of the system and brieﬂy address our

future work. Our web-based tutoring application is

available at http://www.ailab.si/chesstutor.

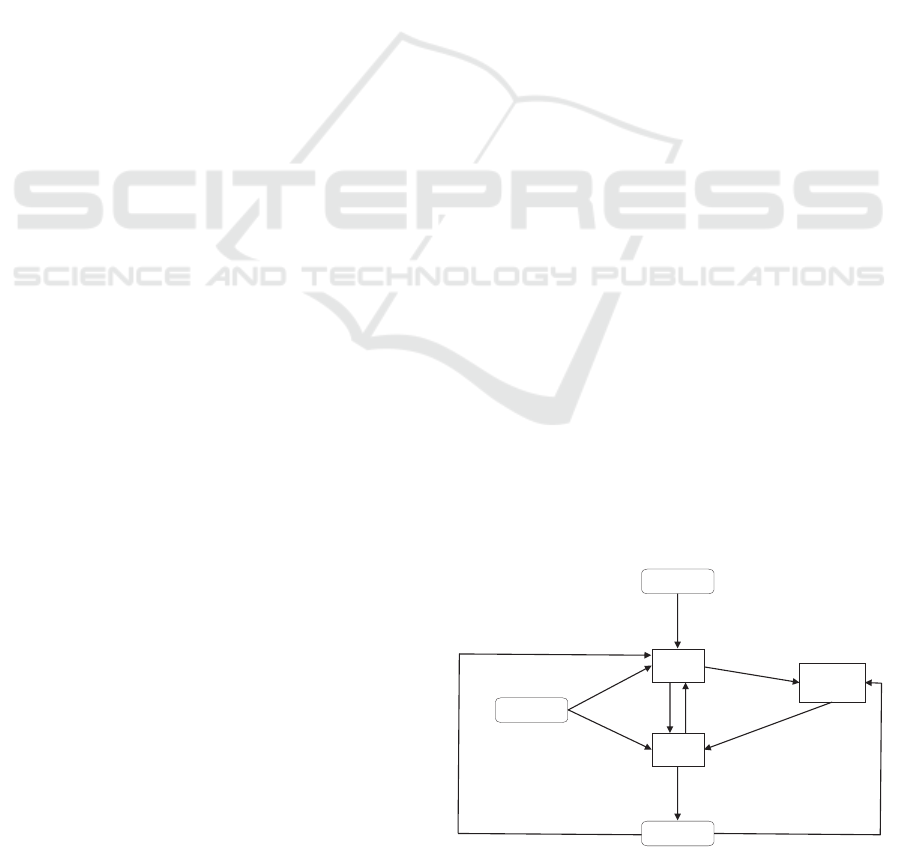
2 ARCHITECTURE

The basic architecture of our chess-endgame tutor is

demonstrated in Fig. 1. The tutor uses three types of

knowledge for teaching chess endgames:

• expert knowledge about the target chess endgame,

stored in the domain model,

• pedagogical knowledge about the teaching strate-

gies in this endgame, represented in the tutoring

model,

• knowledge about the student and his or her learn-

ing progress, stored in the student model.

The other two components are the user interface,

where the student and the tutor interact, and a

search engine that enables the tutor to verify student

problem-solving solutions and to generate appropri-

ate feedback when required.

TUTOR

Engine

Student Model

Tutoring Model

User

Interface

Domain Model

Figure 1: The chess-endgame tutor architecture. The arrows

represent the data ﬂow between individual components, and

the numbers show the time order of the data interchange in

a tutoring session.

2.1 A Cycle in the Tutoring Session

In a typical problem-solving session with the student,

263

Guid M., Možina M., Bohak C., Sadikov A. and Bratko I..

Building an Intelligent Tutoring System for Chess Endgames.

DOI: 10.5220/0004389102630266

In Proceedings of the 5th International Conference on Computer Supported Education (CSEDU-2013), pages 263-266

ISBN: 978-989-8565-53-2

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

the task of the tutor is to present a chess problem

(chess position with a suitable goal) with respect to

the student’s abilities and her current state of knowl-

edge about the domain. For example, if the stu-

dent has just failed to achieve the given goal from

the same position on her previous attempt, the tutor

may present additional information in various possi-

ble forms (e.g. hints, additional instructions, colored

squares and arrows on the chessboard, etc.) to aid the

student.

The student’s solution to the problem, or a solu-

tion step, is received through the user interface. This

information is validated on the ﬂy in real-time by the

search engine, to verify whether the student’s move

leads to the achievement of the given goal. If not, the

tutor warns the student about the error, and the student

can restart the problem or investigate why her solution

is inappropriate. The search engine also plays an im-

portant role in the selection of a goal to be achieved

next. The rules from the domain model are used to

identify the candidate goals, and the search engine

then evaluates which of these goals are achievable.

Based on so-called malrules in the domain model, it

may also detect possible misconceptions in the stu-

dent’s knowledge.

The output of the search engine represents the ba-

sis for the selection of the next tutorial action, and for

an update of the student model. The tutor’s represen-

tation of the student is available to her in a form of

a skill meter, which represents an estimate of the stu-

dent’s mastery of particular skills (or goals). The skill

meter is updated, and the tutor goes to the next cycle.

Fig. 3 displays the user interface of the tutor. On

the top of the screen there is the navigation panel that

enables switching between tutor mode and play mode

(see Section 2.3 for explanations), access to instruc-

tions and example games, and information about the

time spent. On the left-hand side there is a large chess

board, with navigation buttons and last few moves

played below. On the right-hand side there is a space

for tutorial actions and the skill meter.

2.2 Domain Model

Chess endgames are a well-deﬁned problem-solving

domain. Even elementary chess endgames can be suf-

ﬁciently complex and thus interesting to learn. In an

endgame of king, bishop, and knight versus a lone

king (also known as KBNK), for example, even op-

timal play in a checkmating procedure may take as

many as 33 moves. There are many recorded cases

when strong players, including grandmasters, failed

to win this endgame.

We use a rule-based domain model. This type

of domain models is typical for cognitive tutors that

proved to be successful in improving student learning

in a range of learning domains (Anderson et al., 1995;

Koedinger et al., 1997; Koedinger and Corbett, 2006).

The domain model was obtained semi-automatically

as a result of domain conceptualization, as presented

in (Mo

zina et al., 2012) and (Guid et al., 2009).

2.2.1 Conceptualization of Domain Knowledge

Conceptualization of learning domains can be viewed

as one of the key components in the construction of

intelligent tutoring systems. The role of domain con-

ceptualization is as follows. In complex domains, the

connection between the basic domain theory (axioms,

laws, formulas, rules of the game, etc.) and prob-

lem solutions is usually rather complex and hard for

a human to execute. Therefore, there is typically a

need for an intermediate theory, conceptualized do-

main theory, which serves as a bridge between the ba-

sic declarative domain theory and procedural knowl-

edge for concrete problem solving.

In terms of a derivation chain, the basic domain

theory (axioms, etc.) logically entails a “conceptu-

alized domain theory,” which in turn entails prob-

lem solutions. Logically, the basic domain theory

also entails problems solutions, but at much higher

problem-solving effort. The basic theory is typi-

cally “non-operational” for a human (requires exces-

sive computation, or it may be too complex to mem-

orize), whereas the conceptualized theory is “human-

assimilable.” These relations are illustrated in Fig. 2.

original theory

problem solution

original theory

problem solution

conceptualized domain theory

Figure 2: The result of a domain conceptualization. Arrows

indicate derivation, and the length of an arrow indicates the

complexity of the derivation.

A conceptualized domain is a problem-solving

tool for a human, and therefore should be simple and

compact, so that it can be understood, memorized,

and executed by the student.

Fig. 4 shows a problem state space in a typical

problem-solving setting. The circles represent prob-

lem states, and arrows represent available actions. In

domains of any interest the solution path requires too

excessive computation, or it is too difﬁcult to memo-

rize for a student. To alleviate the student’s task, we

learn intermediate goals that can lead the student reli-

ably towards the solution of the problem (see Fig. 5).

Our rule-based model consists of no more than 11

production rules, i.e., if-then statements suggesting

goals to be achieved when some conditions are met.

They are slightly adapted from (Guid et al., 2009).

CSEDU2013-5thInternationalConferenceonComputerSupportedEducation

264

Figure 3: The chess-endgame tutor user interface.

Each production rule contains one goal, achievable

in d plies (i.e. half-moves). This depth parameter

is ﬁxed and is set prior to conceptualization of do-

main knowledge. It enables to adapt the level of con-

ceptualization to the skill level of a targeted group of

students, since it determines to some extent the com-

plexity of learned rules (Mozina et al., 2010).

The goals are achievable in up to d plies, typi-

cally in several possible ways and move orders. The

search engine veriﬁes on the ﬂy whether the student’s

move is correct or incorrect in the sense of achieving

the given goal. Moreover, the search engine can also

evaluate whether the move is acceptable (in terms of

approaching to checkmate) even in cases when it ac-

tually fails to achieve of the goal – in such a case the

student will receive a different type of feedback as if

the move was entirely bad.

2.3 Tutoring Model

The cognitive theory underlying our chess-endgame

tutor is compatible with the ACT-R learning theory

PROBLEM STATE SPACE

start node

. . .

(too) long

solution path

. . .

solution path

. . .

goal nodes

Figure 4: Problem state space in interesting domains.

(Anderson and Lebiere, 1998). The model-tracing

approach to intelligent tutoring is used: the tutor as-

sesses and interprets students’ solution steps by com-

paring what the student does in any given situation

against the appropriate rule in the domain model (An-

derson et al., 1995). The production rules guide a

student reliably towards the ﬁnal goal of achieving

checkmate within the allowed 50 moves, even with

a slowest possible realization of strategic goals (Guid

et al., 2009).

The tutor operates in two different modes:

Tutor Mode. represents the main learning environ-

ment and thus the most important part of the tu-

tor. It enables the student to practice her skills

in a problem-solving context, executing suggested

goals and receiving feedback by the tutor.

Play Mode. enables the student to test or practice her

skills in playing the endgame against the com-

puter, without any interventions by the tutor. The

student only has basic hints on disposal, given on

demand only. No move retracts are possible.

Beside text-based explanations the tutor also has an

LEARNING INTERMEDIATE GOALS

start nodes of

intermediate goals

. . .

goal nodes of

intermediate goals

. . .

intermediate goals

. . .

Figure 5: The role of intermediate goals.

BuildinganIntelligentTutoringSystemforChessEndgames

265

option to use colors and arrows on the chessboard dis-

play when giving feedback to the student. For exam-

ple, to mark the squares that limit the area available to

the opponent’s king.

2.4 Student Model

In our chess-endgame tutor, the role of the student

model is primarily to help correct “incomplete” stu-

dent knowledge, and to help diagnose bugs in the

student’s knowledge. The knowledge is represented

in a form of a skill meter (see Fig. 3 on the right

side), aiming to show the level of student’s under-

standing of particular skills. Each of the skills cor-

responds to one production rule in the domain model.

We use one of the most popular methods for estimat-

ing students’ knowledge, that is Bayesian Knowledge

Tracing model (Corbett and Anderson, 1995). The

model uses four parameters per skill, which were in

our case tuned arbitrarily with the help from a chess

expert and will be continuously updated using student

performance data, to relate performance to learning

as well as possible. We use an open student model

to support students in evaluating their own learning

(Bull and Kay, 2007). The skill meter may assist the

student in making the choice of which skill to focus

on: the tutor allows the student to pick a random posi-

tion featuring the goal associated with particular skill.

3 CONCLUSIONS AND FUTURE

WORK

We followed some commonly accepted guidelines for

building intelligent tutoring systems and applied them

to the domain of chess endgames. The tutor is based

on a rule-based domain model that represents the re-

sult of using our methods for semi-automatic domain

conceptualization (Mo

zina et al., 2012).

The main line of the future work is to evaluate the

proposed system. This includes both:

• Summative Evaluation: to examine the overall ed-

ucational impact of the tutor,

• Formative Evaluation: to assess the effectiveness

of the evolving design, in particular with respect

to usability of our semi-automatically derived do-

main model.

One of the features of our web-based application is an

ability to record students’ actions and times spent on

executing them. These data will represent the basis

for an assessment of student acquisition of skills and

understandings. As another aspect of the evaluation,

we intend to evaluate the applications’ usefulness and

its pedagogical abilities (Giannakos, 2010).

We also plan to extend the domain model to in-

clude several additional chess endgames.

REFERENCES

Anderson, J., Corbett, A., Koedinger, K., and Pelletier, R.

(1995). Cognitive tutors: Lessons learned. The Jour-

nal of the Learning Sciences, 4(2):167–207.

Anderson, J. R. and Lebiere, C. (1998). The atomic com-

ponents of thought. Lawrence Erlbaum Associates,

Mahwah.

Bull, S. and Kay, J. (2007). Student models that invite the

learner in: The smili open learner modelling frame-

work. International Journal of Artiﬁcial Intelligence

in Education, 17(2):89–120.

Corbett, A. and Anderson, J. (1995). Knowledge trac-

ing: Modeling the acquisition of procedural knowl-

edge. User Modeling and User-Adapted Interaction,

4(4):253–278.

Giannakos, M. N. (2010). The evaluation of an e-learning

web-based platform. In Proceedings of the 2nd Inter-

national Conference on Computer Supported Educa-

tion, pages 433–438. SciTePress.

Guid, M., Mo

zina, M., Sadikov, A., and Bratko, I. (2009).

Deriving concepts and strategies from chess table-

bases. In ACG, pages 195–207.

Kazemi, F., Yektayar, M., and Abad, A. M. B. (2012).

Investigation the impact of chess play on develop-

ing meta-cognitive ability and math problem-solving

power of students at different levels of education. Pro-

cedia - Social and Behavioral Sciences, 32:372 – 379.

Koedinger, K., Anderson, J., Hadley, W., and Mark, M.

(1997). Intelligent tutoring goes to school in the big

city. International Journal of Artiﬁcial Intelligence in

Education, 8(1):30–43.

Koedinger, K. and Corbett, A. (2006). Cognitive tutors:

Technology bringing learning sciences to the class-

room. In Sawyer, R., editor, The Cambridge hand-

book of the learning sciences, pages 61–78. Cam-

bridge University Press, New York.

zina, M., Guid, M., Sadikov, A., Groznik, V., and

Bratko, I. (2012). Goal-oriented conceptualization of

procedural knowledge. In Lecture Notes in Computer

Science, volume 7315, pages 286–291.

Mozina, M., Guid, M., Sadikov, A., Groznik, V., Krivec,

J., and Bratko, I. (2010). Conceptualizing procedural

knowledge targeted at students with different skill lev-

els. In de Baker, R. S. J., Merceron, A., and Jr., P. I. P.,

editors, EDM, pages 309–310.

CSEDU2013-5thInternationalConferenceonComputerSupportedEducation

266