CTSiM: A Computational Thinking Environment for Learning

Science through Simulation and Modeling

Satabdi Basu

, Amanda Dickes

, John S. Kinnebrew

, Pratim Sengupta

, and Gautam Biswas

Institute for Software Integrated Systems (ISIS) & EECS Dept, Vanderbilt University, Nashville, TN 37212, U.S.A.

Department of Teaching and Learning, Peabody College, Vanderbilt University, Nashville, TN 37235, U.S.A.

Keywords: Computational Thinking, Agent-based Modeling, Simulations, Visual Programming, Learning-by-Design,

Scaffolding, Science Education.

Abstract: Computational thinking (CT) draws on fundamental computer science concepts to formulate and solve prob-

lems, design systems, and understand human behavior. CT practices (e.g., problem representation, abstrac-

tion, decomposition, simulation, verification, and prediction) are also central to the development of exper-

tise in a variety of STEM disciplines. Exploiting this synergy between CT and STEM disciplines, we have

developed CTSiM, a cross-domain, scaffolded, visual-programming and agent-based learning environment

for middle school science. We present and justify the CTSiM architecture and its implementation. To identi-

fy challenges and scaffolding needs in learning with CTSiM, we present a case study describing the chal-

lenges that a high- and a low-achieving student faced while working on kinematics and ecology units using

CTSiM. Decreases in the number of challenges for both students over sequences of related activities illus-

trate the combined effectiveness of our approach. Further, the specific challenges and scaffolds identified

suggest the design of an adaptive scaffolding framework to help students develop a synergistic understand-

ing of CT and science concepts.

1 INTRODUCTION

Science education in K-12 classrooms has been a

topic of growing importance. The National Research

Council framework for K-12 science education

(NRC, 2011) includes several core science and engi-

neering practices: asking questions and defining

problems, developing and using models, planning

and carrying out investigations, analyzing and inter-

preting data, using mathematics and computational

thinking, and constructing explanations and design-

ing solutions. Several of these epistemic and repre-

sentational practices central to the development of

expertise in STEM disciplines are also primary

components of Computational Thinking (CT). CT

involves formulating and solving problems, design-

ing systems, and understanding human behavior by

drawing on the fundamental concepts of computer

science (Wing, 2010). Specifically, CT promotes ab-

straction, problem representation, decomposition,

simulation, and verification practices. Thus it is not

surprising that CT is included as a key feature in

NRC’s K-12 science education framework. In fact,

several researchers suggest that programming and

computational modeling can serve as effective vehi-

cles for learning challenging STEM concepts (Guz-

dial, 1995; Sherin, 2001; Hambrusch et al., 2009).

In spite of the observed synergies between CT

and STEM education, empirical studies have shown

that balancing and exploiting the trade-off between

the domain-generality of CT and the domain-

specificity of scientific representations, presents an

important educational design challenge (Sengupta et

al., 2012a). Thus, Sengupta et al. (2012b, 2013) and

Basu et al. (2012) proposed CTSiM (Computational

Thinking in Simulation and Modeling) for K-12 sci-

ence learning using a computational thinking ap-

proach. CTSiM provides an agent-based, visual pro-

gramming interface for constructing executable

computational models and allows students to exe-

cute their models as simulations and compare their

models’ behaviors with that of an expert model.

In this paper, building upon our previous work,

we present key design principles and their transla-

tion to details of the CTSiM architecture (Sengupta

et al., 2013; Basu et al., 2012). In an initial study

with 6th-grade students in a middle Tennessee pub-

lic school, students showed high pre-post learning

gains and a good understanding of the basic science

369

Basu S., Dickes A., S. Kinnebrew J., Sengupta P. and Biswas G..

CTSiM: A Computational Thinking Environment for Learning Science through Simulation and Modeling.

DOI: 10.5220/0004390103690378

In Proceedings of the 5th International Conference on Computer Supported Education (CSEDU-2013), pages 369-378

ISBN: 978-989-8565-53-2

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

concepts. However, students also faced a number of

challenges while working with CTSiM. This paper

presents a case study that discusses the challenges

that a high and a low achieving student faced while

working on a physics and a biology unit using

CTSiM. We compare and contrast the challenges

faced by the two students, and discuss how the chal-

lenges evolved over time. The set of challenges, and

the scaffolding provided to help overcome them,

suggest the design of an adaptive scaffolding

framework to help students develop a synergistic

understanding of CT and science concepts.

2 CTSiM DESIGN PRINCIPLES

AND ARCHITECTURE

This section discusses a set of key principles that

guide the design and implementation of CTSiM

(Sengupta et al., 2012b, 2013; Basu, et al., 2012).

The design principles and the corresponding imple-

mentation decisions are summarized in Table1.

2.1 CTSiM Design Principles

Wing’s notion of CT (Wing, 2010) emphasizes ab-

stractions and the automation of abstractions. In

computer science, abstractions represent generaliza-

tions and parametric forms of code segment instanc-

es. They capture essential properties common to a

set of objects while hiding irrelevant distinctions

among them. According to Wing, the “nuts and

bolts” in CT involve defining multiple layers of ab-

straction, understanding the relationships between

the layers, and deciding what details need to be

highlighted (and complementarily, what details can

be ignored) in each layer. This led to our first 2 de-

sign principles (DP) -

DP1: Engage students in defining multiple layers of

computational abstractions to represent different

aspects of the domain, and

DP2: Help students understand relations between

the abstraction layers by mechanizing the relation-

ships.

Another important characteristic of CT is its fo-

cus on conceptualization and developing ideas on

how to solve a problem rather than producing soft-

ware and hardware artifacts that represent the solu-

tion to a problem. This forms the basis for

DP3: Help students conceptualize phenomena rather

than program them using rigid syntax and seman-

tics.

When CT mechanisms are anchored in real-world

problem contexts, programming and computational

modeling become easier to learn (Hambrusch et al.,

2009). Also, reorganizing scientific and mathemati-

cal concepts around computational mechanisms

lowers the learning threshold, especially in domains

like physics and biology (Redish and Wilson, 1993).

Learning environments that adopt this approach

need to make the CT principles explicit and easy to

apply, without limiting the range of phenomena that

can be modeled (high-ceiling) and the types of arti-

facts that can be studied (wide-walls), to make them

widely applicable in K-12 classrooms (Sengupta et

al., 2012b). This leads to two additional principles:

DP4: Make the learning environment encompass

wide-walls and high-ceilings to provide a common

set of principles for studying multiple STEM disci-

plines, and

DP5: Make the CT principles in a domain and the

computational commonalities across domains ex-

plicit and easy to use.

The rest of our design principles draw on the model-

ing literature. Modeling – the collective action of

developing, testing and refining models - has been

described as the core epistemic and representational

practice in the sciences (Lehrer and Schauble, 2006).

Using this we establish:

DP6: Adopt a modeling paradigm which is intuitive

and easily understandable by K-12 students.

We choose an agent-based modeling paradigm

since it is believed to productively leverage students’

pre-instructional intuitions, and it helps in learning

of complex systems and emergent phenomena in

science domains (Wilensky and Reisman, 2006).

Logo (Papert, 1980), a well-known agent-based pro-

gramming language used to support children’ learn-

ing through the creation of artifacts, facilitates sim-

ultaneous learning of concepts about the domain

phenomena and computational concepts, such as

procedure abstraction, iteration, and recursion.

Also, to help students seamlessly progress

through cycles of algorithm construction, visualiza-

tion, analysis, reflection and refinement with timely

feedback, we have

DP7: Incorporate multiple “liveness” factors as

support for programming and learning by design.

After model construction, learning is believed to

occur by comparing the model behavior against that

of a correct model or real world data. Thus, we have

DP8: Enable verification and validation of computa-

tional models.

Finally, to help students model real-world phe-

nomena and to apply their skills learnt through mod-

eling to real world problems, we have

DP9: Draw on engineering thinking by building sys-

CSEDU2013-5thInternationalConferenceonComputerSupportedEducation

370

tems that model and interact with the real world.

2.2 Implementing Design Principles:

The CTSiM Architecture

We base the conceptual framework for our pedagog-

ical approach on a typical learning-by-design se-

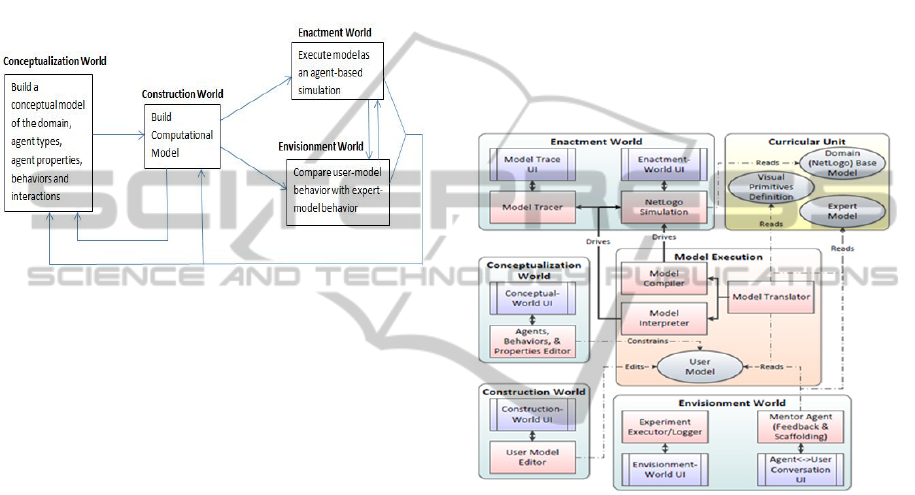
quence. Figure 1 depicts the CTSiM activity se-

quence which integrates our conceptual framework

with the agent-based modeling paradigm.

Figure 1: Sequence of activities performed by a student in

the CTSiM learning environment.

Initially, students conceptualize the science phe-

nomena by structuring it in terms of the types of

agents involved, their properties, behaviors, and in-

teractions in what we call the ‘Conceptualization

World’. They then construct computational models

describing the behavior of each agent type in the

Construction or C-World. Engaging students in

modeling at two different levels of abstraction helps

implement DP1. Students can view another layer of

abstraction by executing their models as agent-based

NetLogo simulations (Wilensky, 1999) in the En-

actment or E-World. Following DP2, the agent types

and properties specified in the conceptual model de-

termine what students can model in the C-World.

Similarly, the computational models constructed de-

termine what students see in the E-World. Students

can also verify the correctness of their models by

comparing the simulations generated by their models

against ‘expert’ simulations in the Envisionment or

V-World (this implements DP8).

The next design decision involved choosing a

mode of programming for the C-World to enable

students to represent phenomena computationally

without having to learn the syntax and semantics of

a programming language (see DP3).

We focus on visual programming (VP) as the

mode of programming to make it easier for middle

school students to translate their intuitive knowledge

of scientific phenomena (whether correct or incor-

rect) into executable models (Sengupta et al., 2012b,

2013). In such environments, students typically con-

struct programs using graphical objects in a drag-

and-drop interface (Kelleher and Pausch, 2005).

This significantly reduces students’ challenges in

learning the language syntax (compared to text-

based programming), and thus makes programming

more accessible to novices. Unlike some agent-

based VP environments like AgentSheets (Repening,

1993), StarLogo TNG (Klopfer et al., 2005), Scratch

(Maloney et al., 2004), and Alice (Conway, 1997),

which have often been employed with game design

as the core programming activity, our goal is to fo-

cus on using VP to support scientific modeling and

simulation.

Figure 2: The CTSiM architecture.

The CTSiM C-World consists of a library of vis-

ual primitives from which students can choose prim-

itives and spatially arrange them to generate their

computational models. These primitives include

both domain-specific and domain-general primitives

(Sengupta et al., 2013). The set of available visual

primitives may vary with the domain or curricular

unit being modeled. Different curricular units of

varying complexities can be defined by specifying

(i) a set of available visual primitives, (ii) an expert

computational model using these primitives, and (iii)

a NetLogo-based domain model (implements DP4).

Some of these visual primitives are specific to the

domain being modeled, while others related to CT

principles are domain-general and can be reused

across domains (in accordance with DP5). The visu-

al primitives are internally translated to an interme-

diate language (a limited set of computational

primitives), which is then compiled into NetLogo

code to generate a simulation corresponding to the

CTSiM:AComputationalThinkingEnvironmentforLearningSciencethroughSimulationandModeling

371

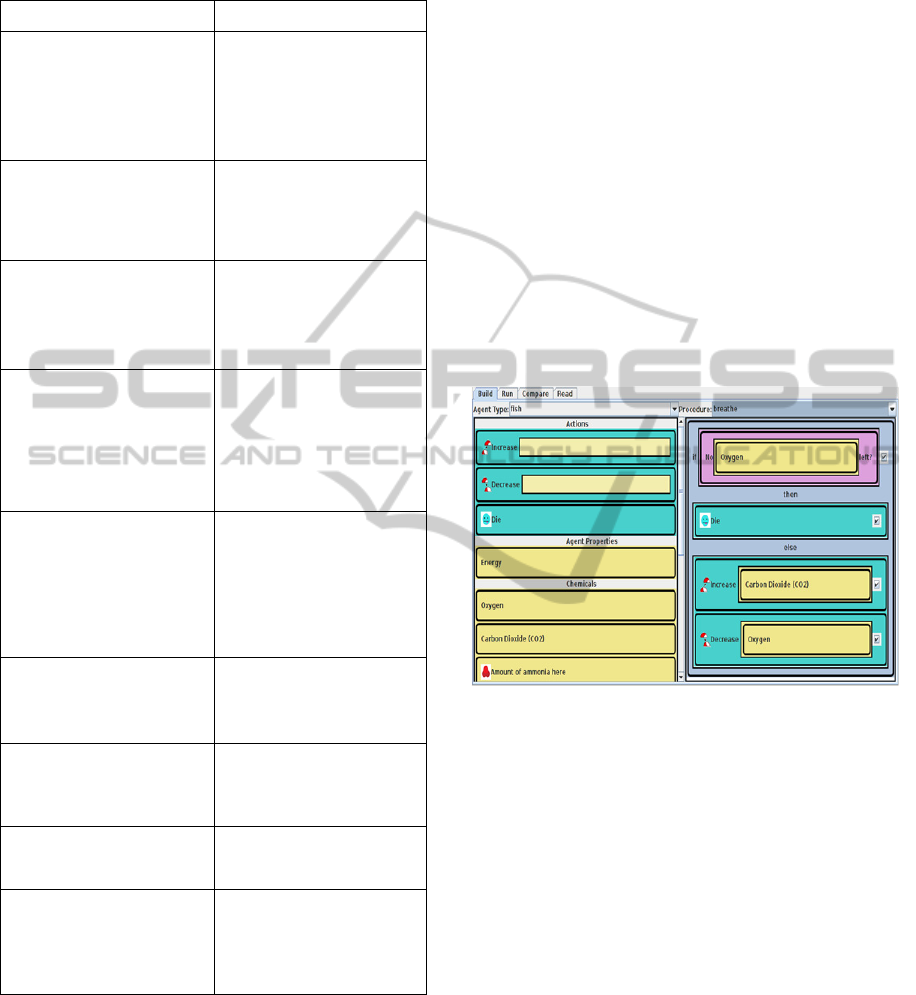
Table 1: Design principles and corresponding implementa-

tion decisions.

Design Principles (DP) Implementation Decisions

DP1: Engage students in

defining multiple layers of

computational abstractions to

represent different aspects of

the domain

Students construct conceptu-

al models (structural and be-

havioural layer) and compu-

tational models(functional

layer), and can also execute

their models as simulations

DP2:

Help students under-

stand relations between the

abstraction layers by mecha-

nizing the relationships

Conceptual model deter-

mines available primitives in

the C-World, Computational

model determines simulation

DP3:

Help students

conceptualize phenomena

rather than program them

using rigid syntax and

semantics

Employ a drag-and-drop

visual programming

interface

DP4:

Make the learning en-

vironment encompass wide-

walls and high-ceilings to

provide a common set of

principles for studying mul-

tiple STEM disciplines

Ability to define any domain

in terms of a base model in

NetLogo, a list of available

primitives, and an expert

computational model using

those primitives

DP5: Make the CT principles

in a domain and the compu-

tational commonalities

across domains explicit and

easy to use

For each domain, define

some visual primitives

which are domain-specific

and others which are do-

main-general; re-use the

domain-general primitives

across multiple domains

DP6: Adopt a modeling par-

adigm which is intuitive and

easily understandable by K-

12 students

Employ an agent-based

modeling/programming

paradigm

DP7: Incorporate multiple

“liveness” factors as support

for programming and learn-

ing by design

Include functionalities for

code-highlighting, and

commenting out code

DP8: Enable verification and

validation of computational

models

Implement the Enactment

and Envisionment worlds

DP9: Draw on engineering

thinking by building systems

that model and interact with

the real world

Make students analyze real

world data in the conceptual-

ization phase; Then, apply

concepts learnt to real

world problems

user model. Figure 2 presents the architecture for the

CTSiM learning environment. In Section 3, we de-

scribe the details of the different components of the

architecture which we have already implemented.

Other components like the Conceptualization World

will be implemented in future versions of CTSiM.

3 CTSiM IMPLEMENTATION

3.1 The Construction or C-World

The C-World allows students to build computational

models using an agent-based, visual programming

interface (see Figure 3). The students choose the

type of agent and procedure they are modeling at the

top of the screen. A list of visual primitives, along

with corresponding icons, is provided on the left

pane. These primitives are of three types: agent ac-

tions (e.g., moving, eating, reproducing), sensing

conditions (e.g., vision, color, touch, toxicity), and

controls for regulating the flow of execution in the

computational model (e.g., conditionals, loops). Stu-

dents drag and drop these available primitives onto

the right pane, arranging and parameterizing them

spatially to construct their models.

Figure 3: Construction world with a ‘breathe’ procedure

for ‘fish’ agents in a fish-tank unit.

3.2 The Enactment or E-World

The E-World allows students to define a scenario

(by assigning initial values to a set of parameters)

and visualize the multi-agent-based simulation driv-

en by their computational model, as seen in Figure 4.

CTSiM, written in Java, includes an embedded

NetLogo instance to implement the simulation. Stu-

dents’ models are represented in the system as code

graphs of parameterized computational primitives.

These code graphs remain hidden from the end-user

(the learner), and are translated into NetLogo com-

mands to generate the simulations. NetLogo visuali-

zations and plotting functionalities provide the stu-

dents with a dynamic, real-time display of how their

agents operate in the microworld, thus making ex-

plicit the emergence of aggregate system behaviours.

CSEDU2013-5thInternationalConferenceonComputerSupportedEducation

372

Figure 4: The Enactment world for a fish-tank unit.

Furthermore, CTSiM supports model tracing,

meaning that the system can highlight each primitive

in the C-World as it is being executed in the E-

World (implements DP7). In order to achieve nor-

mal speed of execution, the ‘model trace runner’ is

treated as an alternate model execution path availa-

ble in the E-World (see Figure 2) where each visual

primitive is translated separately via the Model In-

terpreter, instead of the entire user model being

translated to NetLogo code. Such supports for mak-

ing algorithms “live”, helps students better under-

stand the correspondence between their models and

simulations, as well as identify and correct model er-

rors. CTSiM also supports execution of subsets of

the code in the C-World through the standard pro-

gramming practice of “commenting out” parts of the

computational model, allowing students to test their

models in parts. These functionalities can be lever-

aged to provide important scaffolding that supports

model refinement and debugging activities.

3.3 The Envisionment or V-World

The V-World allows students to systematically de-

sign experiments to test their constructed models and

compare their model behaviours against that of an

“expert” model, as seen in Figure 5. Although the

expert model itself is hidden, students observe its

behaviour, comparing it with their own models,

through side-by-side plots and microworld visualiza-

tions. Additional scaffolding will help students de-

cide what components of their models they need to

investigate, develop further, or check for errors, and

propose corrective actions.

3.4 The Computational Language

At the high level, our computational language com-

prises the visual primitives available to the end user

in the C-World, as described in Section 3.1. Each

Figure 5: The Envisionment world for a fish-tank unit.

visual primitive, in turn, is defined in terms of one or

more underlying computational primitives with ap-

propriate constraints and parameters, to form what

we call ‘code graphs’. The computational primitives

provide a domain-independent set of computational

constructs in a limited set of categories. Since the

expert model in CTSiM is described using the same

set of visual primitives available to the students,

both student-built and pre-defined expert models can

be executed, analyzed, and compared using the same

computational language. Finally, this intermediate

language of computational primitives is translated to

NetLogo code to produce the E and V world simula-

tions.

For example, Figure 4 shows a visual primitive

‘Increase’ with the argument (another visual primi-

tive) ‘Carbon Dioxide (CO

)’. The CO

block is

simply defined by a single computational primitive

corresponding to the environment (global) variable

for CO

. However, because of the goals and target

grade-level of this unit, the student does not specify

any other (e.g., quantitative) arguments for the ‘In-

crease’ block. Instead, the appropriate quantities for

the simulation are part of the computational defini-

tion of the ‘Increase’ visual primitive, which is actu-

ally a series of checks corresponding to the possible

visual primitives that could be provided as argu-

ments to ‘Increase’. For each possible visual primi-

tive (e.g., the CO

block used in the example), the

computational definition specifies the quantity by

which the primitive’s value should be increased.

Since the computational primitives are constant for

all units, the same model translator can analyse or

execute students’ models with different unit-specific

visual primitives.

3.5 The Model Executor

In CTSiM, the model executor (see Figure 2), trans-

lates a (student-built or expert) model into corre-

CTSiM:AComputationalThinkingEnvironmentforLearningSciencethroughSimulationandModeling

373

sponding NetLogo code, which is then combined

with the domain base model. The base model pro-

vides NetLogo code for visualization and other

housekeeping aspects of the simulation that are not

directly relevant to the learning goals of the unit.

The combined model forms a complete, executable

NetLogo simulation, to run in the E or V Worlds.

As seen in Section 3.2, the executor provides an

alternate path through the ‘Model Tracer’. Using the

Model Tracer, instead of translating the entire stu-

dent-generated model into NetLogo code, each visu-

al primitive is translated separately, and highlighted

in the C-World as it is executed.

3.6 Defining New Curricular Units

Defining a new unit using the CTSiM architecture is

fairly straightforward and involves defining the fol-

lowing components: (i) an xml file defining visual

primitives for the unit (in terms of computational

primitives), (ii) an xml file describing how the visual

primitive blocks are to be depicted graphically in the

C-World, including name, positions for arguments,

color, etc., (iii) an xml file describing the expert

computational model using the visual primitives de-

fined for the unit, and (iv) a domain base model

which is responsible for the NetLogo visualization

and other housekeeping aspects of the simulation.

4 METHOD

We describe a study conducted with 6th-grade mid-

dle Tennessee students who worked on two units in

Kinematics and Ecology using CTSiM.

4.1 CTSiM Curricular Units

Kinematics Unit

Kinematics unit activities were divided into three

phases (Basu et al., 2012; Sengupta et al., 2013):

Phase 1: Turtle Graphics for Constant Speed and

Acceleration - Students generated algorithms to

draw simple shapes (squares, triangles and circles)

to familiarize them with programming primitives

such as “forward”, “right turn”, “left turn”, “pen

down”, “pen up” and “repeat”. Students then modi-

fied their algorithms to generate spirals where each

line segment was longer (or shorter) than the previ-

ous one. This exercise introduced students to the

“speed-up” and “slow-down” commands, and al-

lowed them to explore the relationship between

speed, acceleration, and distance.

Phase II: Conceptualizing and Re-representing a

Speed-time Graph - Students generated shapes

where the length of segments was proportional to the

speed in a given speed-time graph. For example, the

initial spurt of acceleration in the graph was repre-

sented by a small growing spiral, the gradual decel-

eration by a large shrinking spiral, and constant

speed by a shape like a triangle, square, and so on.

The focus was on developing mathematical

measures from meaningful estimation and mechanis-

tic interpretations of the graph, and thereby gaining a

deeper understanding of concepts like speed and ac-

celeration.

Phase III: Modeling Motion of an Agent to match

Expert behavior - Students modeled a roller coast-

er’s behavior as it moved on different segments of a

track: up (pulled by a motor), down, flat , and then

up again. Students were first shown a simulation

corresponding to an ‘expert’ roller coaster model in

the V world. Then, they conceptualized and built

their own agent model to match the observed expert

roller coaster behavior for all of the segments.

Ecology Unit

In the Ecology unit students modeled a closed fish

tank system in two steps: (1) a macro-level semi-

stable model for fish and duckweed; and (2) a micro-

level model of the waste cycle with bacteria. The

macro model required modeling the food chain, the

respiration and reproductive processes of the fish

and duckweed, and the macro-level elements of the

waste cycle. The non-sustainability of the macro-

model (the fish and the duckweed gradually died

off), encouraged students to reflect on what might be

missing from the model, prompting the transition to

the micro model. They identified the continuously

increasing fish waste as the culprit, and this trig-

gered the introduction of bacteria in the system.

At the micro level, students modeled the waste

cycle with bacteria converting the toxic ammonia in

the fish waste to nitrites, and then nitrates, which

sustained the duckweed. The graphs generated from

the expert simulation helped students understand the

producer-consumer relations between the bacteria

and the chemicals.

4.2 Setting and Study Design

15 6

graders worked on CTSiM outside the class-

room with one-on-one verbal guidance from one of

5 members of our research team (Scaffolded or S-

Group), while the remaining 9 students worked in

the classroom (Classroom or C-Group) with some

instruction from the researchers and the classroom

CSEDU2013-5thInternationalConferenceonComputerSupportedEducation

374

teacher. The C group also received individual help

from the researchers if they raised their hand. The

students were assigned to the groups by their class-

room teacher.

All students worked on the three phases of the

kinematics unit before the ecology macro and micro

units. After completing the ecology micro unit, the S

group received an additional scaffold: they discussed

the combined micro-macro model with their as-

signed researcher and how the two models were

causally linked to support sustainability.

Students worked on the two science units in

hour-long sessions for three days each. The units

provided a natural sequencing in which students first

learned to model and reason with a single agent in

kinematics and then went on to model multiple

agents and their interactions in ecology.

4.3 Assessments

The Kinematics pre/post-test assessed whether

agent-based modeling improved students’ abilities to

generate mathematical representations of motion and

reason causally about them. Specifically, the test re-

quired interpretation of speed versus time graphs and

generating diagrammatic representations to explain

motion in a constant acceleration field. For the Ecol-

ogy unit, the pre/post-test focused on students’ un-

derstanding of the role of species in the ecosystem,

interdependence among the species, the waste and

respiration cycles, and how a change in one species

affected the others.

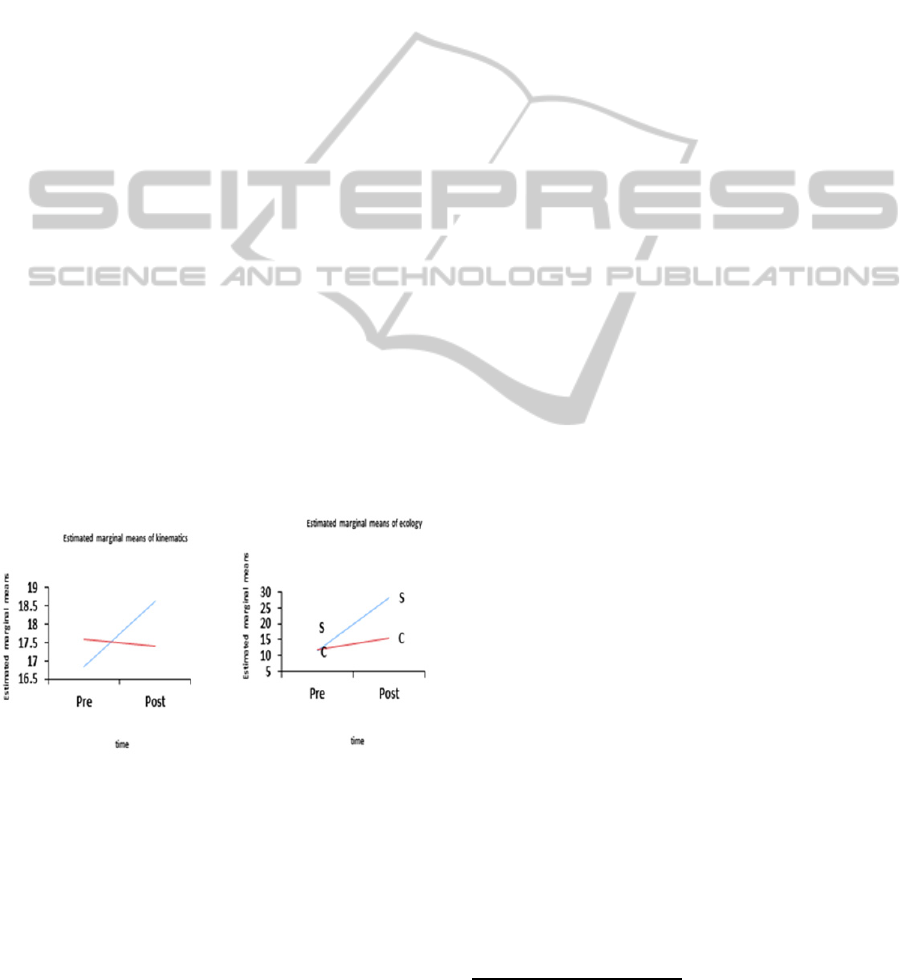
Figure 6: Comparison of gains between groups using

TCAP scores as a covariate.

5 RESULTS

5.1 Learning Gains with CTSiM

The intervention produced statistically significant

gains for the Ecology unit, but not for the Kinemat-

ics unit (Basu et al., 2012), as seen in Table 2. How-

ever, as expected, for both units, the S group, which

received direct one-on-one scaffolding, showed

higher learning gains than the C group.

The lack of statistical significance in the kine-

matics unit may be attributed to a ceiling effect (stu-

dents in both groups had high pre-test scores). In the

ecology unit, significant gains were observed for

both groups, which can be attributed to an increased

awareness of the entities in the fish tank and their re-

lations with other species. However, the supplemen-

tary causal-reasoning activity helped the S-group

students gain a better understanding of the interde-

pendence among the species, compared to the C-

Group, which received minimal scaffolding and

none targeted towards causal reasoning.

To account for prior knowledge differences be-

tween groups, we computed a repeated measures

ANCOVA with TCAP (Tennessee Comprehensive

Assessment Program) science scores as a covariate

to study the interaction between time and condition.

There was still a significant effect of condition on

learning gains in ecology (F(1,21)=37.012,

p<0.001), and a similar trend was seen in kinematics

(F(1,21)=4.101,p<0.06) (Figure 6 shows adjusted

gains).

5.2 Analyzing Students’ Experiences

Along with demonstrating the effectiveness of our

overall approach, we also studied students’ interac-

tions with CTSiM in more depth – the challenges

they faced and the scaffolds they required – in order

to identify areas for improvement and embedded,

adaptive scaffolding in the system. To investigate

students’ conceptual development, we adopted an

explanatory case study approach (Gomm et al.,

2000). In this analysis, we consider two representa-

tive cases from the S-group: Jim and Sara (names

changed to maintain student anonymity).

Based on pre-test responses and TCAP scores,

we chose Jim and Sara because they were repre-

sentative of the high- and low-performing students,

respectively. We contrast their experiences with the

CTSiM units in terms of the number and types of

challenges they encountered. Activities 1-7 in the

analysis refer to: A1 - Kinematics constant speed

shape drawing, A2 - Variable speed shape drawing,

A3 - Re-representing a speed-time graph, A4 - Roll-

er-coaster activity, A5 - Ecology fish-tank macro-

unit, A6 - Fish-tank micro-unit, A7 - Combined fish-

tank macro- and micro-unit.

Number of Challenges

For both Jim and Sara and for both curricular units,

CTSiM:AComputationalThinkingEnvironmentforLearningSciencethroughSimulationandModeling

375

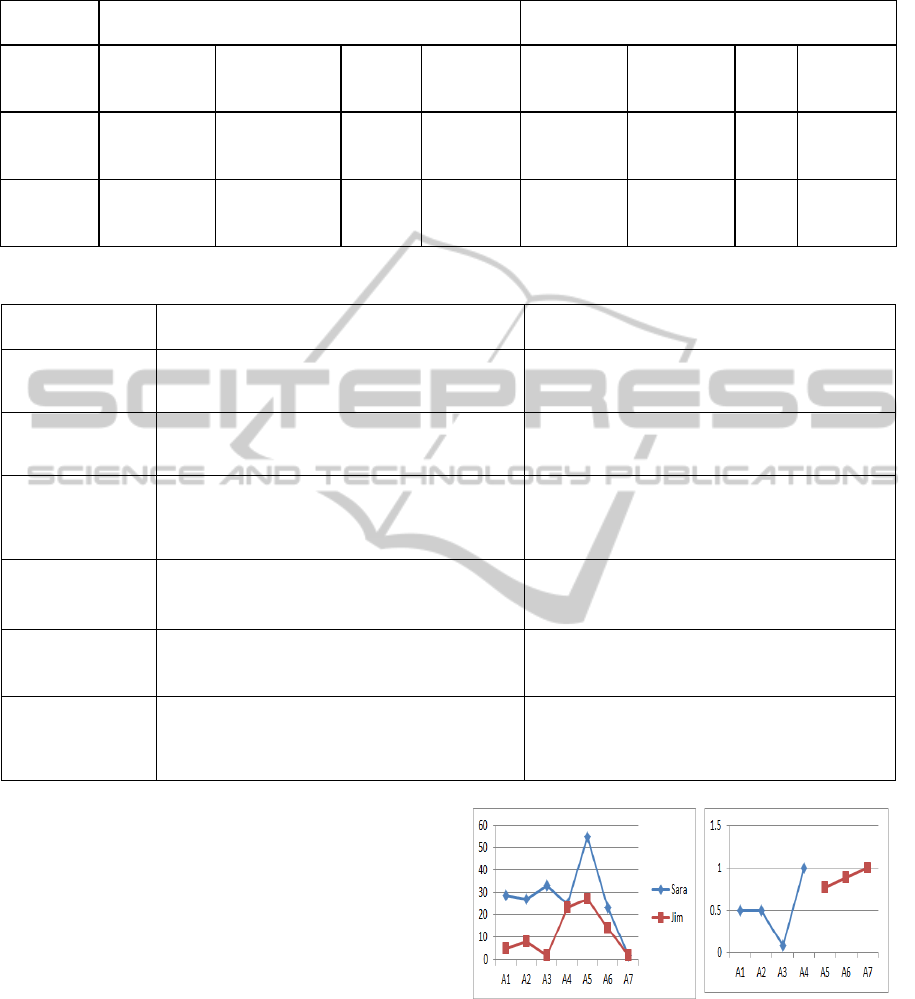
Table 2: Paired t-test results for Kinematics and Ecology pre and post test scores.

Kinematics Ecology

PRE (S.D.)

(max=24)

POST (S.D.)

(max=24)

t-value

P-value

(2-tailed)

PRE (S.D.)

(max=35.5)

POST (S.D.)

(max=35.5)

t-value

P-value

(2-tailed)

S-Group

(n=15)

18.07 (2.05) 19.6 (2.29) .699 0.017 13.03(5.35) 29.4(4.99) 8.664 <0.001

C-Group

(n=9)

15.56 (4.1) 15.78 (4.41) 0.512 0.622 9.61(3.14) 13.78(4.37) 3.402 <0.01

Table 3: Types of programming challenges and scaffolds.

Programming

Challenges

Description of challenges Scaffolds

Syntax and Seman-

tics of Primitives

Difficulty understanding the usage, functionality,

and enactment of certain visual primitives

Step through the code and explain the functionality

of primitives by showing their behaviour in the E-

World; Explain correct syntax for primitives

Procedurality

Difficulty in specifying a task in terms of a finite

set of steps, and ordering the steps correctly to

reach a desired goal

Prompt the student to describe the phenomena and

break it into subparts and the steps within each

subpart.

Modularity

Difficulty in separating the functionality of the

agents into independent modules such that each

module executes only one aspect of the desired

functionality

Prompt student to think about which procedure

they are currently modeling and whether their code

pertains to only that procedure

Code Reuse

Difficulty in identifying already written similar

code to reuse, what parts of similar code to modify

Prompt for analogous reasoning; Making students

think about what similar procedures they have al-

ready written

Conditionals, Loops,

esting, Variables

Difficultly in understanding role of variables, re-

peat-structures, conditionals and how to nest pro-

cedures within other conditional statements

Explain concept of a variable using examples; Ex-

plain syntax and semantics of loops and nested

conditions using code snippets and their enactment

Debugging

Difficulty in methodically finding and reducing

the number of ‘bugs’, or unexpected outcomes, in

the program

Prompts to think about which part of the code

might be causing the bug; help break down the

task by trying to get one code segment to work be-

fore moving onto another.

the number of challenges faced generally decreased

with time for similar units, but went back up when

new computational constructs or modeling complex-

ities were introduced through new activities (see

Figure 7a). In case of Jim, the number of challenges

he faced in the Kinematics unit decreased from A1

to A3, but rose again when he worked

on A4. This

was expected as the roller coaster activity introduced

many new computational constructs like variables,

conditionals, and nesting of blocks. Also, A4 re-

quired students to generate abstractions of a real-

world phenomenon – a more complex modeling task

compared to shape-drawing. Similarly, in the ecolo-

gy unit students had the more complex task of mod-

eling multiple agent types and procedures defining

the behaviour of each agent type.

Expectedly, Jim’s number of challenges is initially

high in the macro model and decreases as he pro-

Figure 7a: Number of

challenges over time.

Figure 7b: Number

(normalized) of similar

challenges over time.

gresses through the micro and combined models. In

the case of Sara, the number of challenges she faced

in the A1-A3, did not decrease like they did for Jim.

The challenges, though scaffolded, persisted through

A1-A3. A potential explanation for this difference is

CSEDU2013-5thInternationalConferenceonComputerSupportedEducation

376

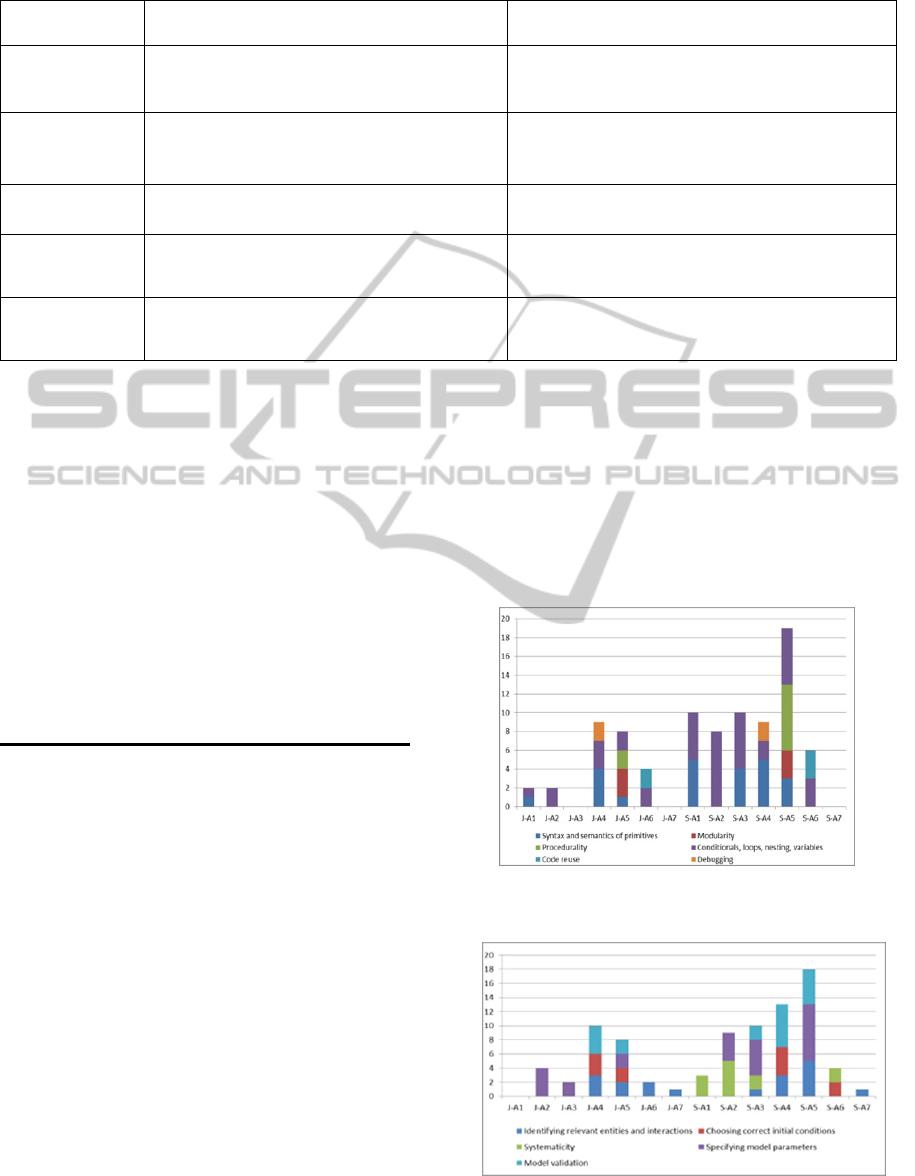
Table 4: Types of modeling challenges and scaffolds.

Modeling

Challenges

Description of challenges Scaffolds

Identifying

Entities and

Interactions

Difficulty in identifying agents to model and

their properties and how they interact with

each other

Point out the appropriate aspects of the phenome-

na that need to be modeled and prompt student to

think about the interactions

Choosing Correct

Initial Conditions

Difficulty in identifying and setting appropri-

ate initial conditions to produce measurable

and observable outcomes

Prompt student to think about the preconditions

necessary for certain functions, Encourage stu-

dents to vary initial conditions

Systematicity

Difficulty in methodical exploration; guessing;

not using sim to inform changes

Encourage student to think about their goal, the

starting point, and their plan of action

Specifying Model

Parameters

Difficulty in determining parameters for the

visual primitive blocks in the C-World

Prompt student to make a parameter change for

more visible output; Encourage testing outcomes

by varying parameter values

Model Validation

Difficulty in verifying and validating model by

comparing and identifying differences with an

expert model

Ask student to slow down the simulation to make

agent actions more visible; Point out the differ-

ences between the user and export model

Jim’s higher initial knowledge of mathematics and

physics, confirmed by the differences in their TCAP

and pre-test scores. However, by the time Sara start-

ed working on A4, the number of challenges she

faced was about the same as Jim’s, indicating that

the CTSiM intervention helped both students in spite

of their initial differences. Moreover, the low per-

forming students seemed to improve their under-

standing of domain and computational constructs,

and, the type of challenges encountered by all stu-

dents gradually became similar, as shown in Figure

7b. The only exception is A3 owing to a floor effect

caused by Jim’s negligible number of challenges in

the activity.

Types of Challenges Faced by Jim and Sara

In order to better understand Jim and Sara’s experi-

ences with CTSiM, we further classified the chal-

lenges and analyzed the scaffolds provided to over-

come them. Most challenges were related to model-

ing and programming, while some were based on the

domain and agent-based-reasoning. A few common

modeling challenges involved guessing turn angles

for shape drawing instead of systematically using a

compass and the E-World to help discover them,

failing to recognize the relationships between ramp

steepness and gravity in changing the speed of the

roller coaster, and choosing forward lengths too

small to produce observable outcomes. Some com-

mon programming challenges included problems

with nesting conditions with and without a motor for

the roller coaster, understanding that ‘swim’ and ‘eat

functionalities had to be separated into different pro-

cedures for a fish, realizing that a fish had to be

hungry as well as have food in order to be able to

eat, etc. Tables 3 and 4 classify the programming

and modeling challenges faced, and the scaffolds

provided by the experimenters to help the students

overcome these challenges.

Figures 8 and 9 depict how the different types of

programming and modeling challenges vary over

time for both Jim and Sara. We see that the trends

are very similar to those seen in Figure 7a for the to-

tal number of challenges over time, especially for

the programming challenges.

Figure 8: Comparison of Programming Challenges per ac-

tivity for Jim (J) and Sara (S).

Figure 9: Comparison of Modeling Challenges per activity

for Jim (J) and Sara (S).

CTSiM:AComputationalThinkingEnvironmentforLearningSciencethroughSimulationandModeling

377

6 CONCLUSIONS

In this paper, we have provided an overview of the

core design principles and architecture of CTSiM – a

learning environment which seamlessly integrates

domain-general CT concepts with domain-specific

representational practices of a variety of STEM dis-

ciplines. Using a kinematics and and an ecology

unit, we show how CTSiM is effective in producing

learning gains for both science topics. We also ex-

plained and classified a variety of challenges (and

corresponding scaffolds) faced by a high- and a low-

performing student while they worked with CTSiM.

Our results indicate that the challenges faced by

these students generally decreased with time for se-

quences of related units, but, as expected, again in-

creased when new computational constructs or mod-

eling complexities were introduced. The decrease in

the number of challenges illustrates the combined ef-

fectiveness of our architecture, curricular unit de-

sign, and scaffolds. Further, the specific challenges

and scaffolds identified lay the groundwork for inte-

grating adaptive scaffolding in CTSiM to help stu-

dents develop a synergistic understanding of CT and

science concepts.

ACKNOWLEDGEMENTS

This work was supported by the NSF (NSF Cyber-

learning grant #1237350).

REFERENCES

Basu, S., Kinnebrew, J., Dickes, A., Farris, A.V.,

Sengupta, P., Winger, J., & Biswas, G. (2012). A Sci-

ence Learning Environment using a Computational

Thinking Approach. In Proceedings of the 20th Inter-

national Conference on Computers in Education (pp.

722-729). Singapore.

Conway, M. (1997). Alice: Easy to Learn 3D Scripting for

Novices, Technical Report, School of Engineering and

Applied Sciences, University of Virginia, Char-

lottesville, VA.

Gomm, R., Hammersley, M. and Foster, P. (2000). Case

Study Method: Key Issues, Key Texts. Sage, Thou-

sand Oaks, CA.

Guzdial M. (1995) Software-realized scaffolding to facili-

tate programming for science learning. Interactive

Learning Environments, 4(1). 1-44.

Hambrusch, S., Hoffmann, C., Korb, J.T., Haugan, M.,

and Hosking, A.L. (2009). A multidisciplinary ap-

proach towards computational thinking for science

majors. In Proceedings of the 40th ACM technical

symposium on Computer science education (SIGCSE

'09). ACM, New York, NY, USA, 183-187.

Kelleher, C. & Pausch, R. (2005) Lowering the barriers

to programming: a taxonomy of programming envi-

ronments and languages for novice programmers,

ACM Computing Surveys, Vol. (37) 83–137.

Klopfer, E., Yoon, S. and Um, T. (2005). Teaching Com-

plex Dynamic Systems to Young Students with Star-

Logo. The Journal of Computers in Mathematics and

Science Teaching; 24(2): 157-178.

Lehrer, R., & Schauble, L. (2006). Cultivating model-

based reasoning in science education. In R. K. Sawyer

(Ed.), The Cambridge handbook of the learning sci-

ences (pp. 371–388). New York: Cambridge Universi-

ty Press.

Maloney, J., Burd, L., Kafai, Y., Rusk, N., Silverman, B.,

and Resnick, M. (2004) Scratch: A Sneak Preview. In

Proc. of Creating, Connecting, and Collaborating

through Computing, 104-109.

National Research Council. (2011). A framework for K-12

Science Education: Practices, Crosscutting Concepts,

and Core Ideas. Washington, DC: The National Acad-

emies Press.

Papert, S. (1980). Mindstorms: children, computers, and

powerful ideas. Basic Books, Inc. New York, NY.

Redish, E. F. and Wilson, J. M. (1993). Student program-

ming in the introductory physics course: M.U.P.P.E.T.

Am. J. Phys. 61: 222–232.

Repenning, A. (1993). Agentsheets: A tool for building

domain-oriented visual programming, Conference on

Human Factors in Computing Systems, 142-143.

Sengupta, P., Farris, A.V, & Wright, M. (2012a). From

Agents to Aggregation via Aesthetics: Learning Me-

chanics with Visual Agent-based Computational Mod-

elling. Technology, Knowledge & Learning. 17 (1-2),

pp 23 - 42.

Sengupta, P., Kinnebrew, J.S., Biswas, G., & Clark, D.

(2012b). Integrating computational thinking with K-12

science education: A theoretical framework. In 4th In-

ternational Conference on Computer Supported Edu-

cation (pp. 40-49). Porto, Portugal.

Sengupta, P., Kinnebrew, J.S., Basu, S., Biswas, G., &

Clark, D. (2013). Integrating Computational Thinking

with K-12 Science Education Using Agent-based

Computation: A Theoretical Framework. Education

and Information Technologies.

Sherin, B. (2001). A comparison of programming lan-

guages and algebraic notation as expressive languages

for physics. International Journal of Computers for

Mathematics Learning: 6, 1-61.

Wilensky, U. (1999). NetLogo. Center for Connected

Learning and Computer-based Modelling (http://

ccl.northwestern.edu/netlogo). Northwestern Universi-

ty, Evanston, IL.

Wilensky, U., & Reisman, K. (2006). Thinking like a

wolf, a sheep or a firefly: Learning biology through

constructing and testing computational theories - An

embodied modelling approach. Cognition & Instruc-

tion, 24(2), 171-209.

Wing, J. M. (2010). Computational Thinking: What and

Why? Link Magazine.

CSEDU2013-5thInternationalConferenceonComputerSupportedEducation

378