
Conformed Identification of the Fundamental Matrix in
the Problem of a Scene Reconstruction, using Stereo
Images
V. Fursov
1,2
and Ye. Goshin
1,2
1
S.P. Korolyov Samara State Aerospace University, Samara, Russia
2
Image Processing Systems Institute of the RAS, Samara, Russia
Abstract. This paper deals with the problem of the fundamental matrix
identification on the basis of corresponding points on stereo images. It is one of
the main problems in a scene reconstruction, using stereo images. This problem
is commonly solved by the error-adaptive algorithm RANSAC. In this research,
this problem is approached in accordance with a conformed identification
principle. The method we propose in this paper ensures higher accuracy of the
3D scene reconstruction.
1 Introduction
This paper is devoted to one of the solutions of the problem of a scene reconstruction.
For the 3D scene reconstruction based on a set of pairs of corresponding points on
stereo images, it is necessary to know the matrices of cameras. If the external
parameters of the cameras are unknown, they can be estimated directly from the
preset corresponding points on the images. The solution of this problem is a serious
issue because the number of the test points is commonly small, thus the terms of
statistical stability are not satisfied, and the prior uncertainty of probabilistic
characteristics of noise models takes place.
If prior probabilistic models are absent, the least-squares method (LS) is commonly
applied. It is known that LS-estimation is optimal when measurement errors have
normal distribution [1, 2], but the LS method loses its efficiency in the presence of
rough errors in the input data. The idea of the LS method improvement by searching
for a noise-free subsystem has been introduced in the research [3]. Similar ideas of
identification, based on different assumptions, are given in [4]. However, due to the
lack of necessary computing power at that time, both of these approaches remained at
the level of theoretical ideas.
Recent years, the estimation methods, in which the stability to rough errors such as
failures is obtained at the cost of a significant increase in the computational
complexity of algorithms, are gaining in popularity. RANSAC is the most widely
used algorithm in the task of 3D-scenes reconstruction of this class [5, 6]. The
conformed identification method proposed in [7] is still another approach to this issue.
The identification algorithm, which is based on the idea of conformed
identification with the consecutive formation of a conformal set of estimates, is
Fursov V. and Goshin Y..
Conformed Identification of the Fundamental Matrix in the Problem of a Scene Reconstruction, using Stereo Images.
DOI: 10.5220/0004393200290037
In Proceedings of the 4th International Workshop on Image Mining. Theory and Applications (IMTA-4-2013), pages 29-37
ISBN: 978-989-8565-50-1
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

considered in the present work. This algorithm provides a significant reduction in
computational complexity, at same time it maintains high accuracy and reliability.
The results of quality metrics comparison of this algorithm and the RANSAC
algorithm for solving the problem of determining fundamental matrix on test stereo
images are given.
2 Problem Definition
Suppose there are two cameras with centers of projections at points O and O'. In the
planes of projections P and P' of these cameras, it is possible to define e and e' points
of intersection of OO' line with the planes P and P’ (epipoles) (Fig. 1). For some point
P of the scene there are epipolar lines l and l’ on the planes of projections (lines of
intersection of the plane OO'P with the planes P and P'), on which the corresponding
points p and p' are projections of the point P on two images.
Fig. 1. The epipolar geometry model.
The corresponding points on the two projections are connected by the fundamental
33
-matrix
F
, in particular, for the corresponding points, which coordinates are set
by 3×1-vectors
x
,
'
x
:
,,1
T
x
uv
,
'',',1
T
xuv
, the condition
(') 0
T
xFx
(1)
where
11 12 13
21 22 23
31 32 33
F
FF
F
FFF
F
FF
, is satisfied.
For a given pair of the corresponding points, the ratio (*) is a homogeneous linear
equation for the coefficients
,
,, 1,3
ij
Fij of the fundamental matrix. For N pairs
(
8N
) of the corresponding points with
33
1F
, it is possible to write the system of
N non-homogeneous linear equations [8]:
yXc
ξ
(2)
where
с is the vector with the required characteristics composed from the
coefficients of the fundamental matrix
F:
30

1 2 8 1112132122 233132
,,,
TT
cc c FFFFF FFFc
(3)
8N
-matrix X and
8N
-vectors y and ξ are defined as
''''''
11 11 1 11 11 1 1 1
1
''''''
2
22 22 2 22 22 2 2 2
''''''
1
1
,,
1
N
NNNNNNNNNNNN
uu uv u vu vv v u v
uu uv u vu vv v u v
uuuvuvuvvvuv
Xyξ
(4)
The
12
,,,
N
are errors, connected with an imprecise coordinate assignment
of the corresponding points.
The problem consists in the estimation
ˆ
c
of the vector of parameters
c
in case of
an unknown
1N
-error vector ξ, using
NM
-matrix X and
1N
-vector y
(
NM
). To solve the tasks of this kind, it is offered to apply the so-called
conformed identification method. The idea of this method can be briefly described as
follows.
The set of the
higher-level subsystems, the dimension of which is
SPN
, is
created of the initial system (1). On each of the subsystems, in turn, the set of the
lower-level subsystems, the dimension of which is
M
SN
, is created. It is
supposed that the matrix X and all possible matrices, composed of its lines, are
nonsingular (if it is not so, the procedure of a preliminary monitoring of the
conditionality and the selection of such subsystems can be provided).
Let
1
ˆ
[]
TT
kkkkkk
cXXXG
y
(5)
is the LS method estimation, calculated on the
k
th
lower-level system, and
,
ˆ
{: 1,}
S
llk P
kC c
is a set of those estimations, belonging to one of 1,
P
N
lC
higher-level subsystems. To describe these sets
l
, the mutual closeness criterion of
the estimates on the corresponding lower-level subsystems is introduced:
2
,,
,1
ˆˆ
,1,,,1,
l
PS
llilj N P
ij
WlCijC
cc
(6)
The problem lies in estimation building on the most
conformal set of estimates
ˆ
,
for which the criterion (3) takes its minimum value. This problem essentially leads to
the determination of the index
ˆ
l
:
ˆ
() min ( )
l
l
Wl W
(7)
Finding the most consistent set of estimates in accordance with (3), (4) is a
computationally time-consuming task. Therefore, these algorithms are usually
implemented on multiprocessor systems, even with a relatively small dimension of
the system (1). Nevertheless, there are some problems associated with the storage of a
large number of estimates, calculated on the lower-level subsystems on every node.
31

In this paper, a conformed identification algorithm modification, which provides a
significant reduction in computational complexity, is considered in more detail in the
next section. The results of the experimental tests of accuracy and reliability of the
proposed modified algorithm in comparison with the algorithm of RANSAC are also
provided. The results are illustrated by solving the problem of weak camera
calibration, which is part of technology of 3D scenes reconstruction based on stereo
images.
3 Consecutive Conformed Identification Algorithm
Let us consider the conformed identification algorithm, in which all generated models
are processed sequentially. We assume that the dimension of the subsystems of the
lower-level is equal to the dimension of the vector of the estimated parameters:
SM
.
Suppose
12
, ,...,
N
kk k are the numbers of the initial system rows (2). Let us
consider an arbitrary the lower-level basic subsystem, which consists of
M
rows
(
M
N
), further designated as
12
, ,...,
M
Sk k k
. Let us define the set
l
of the
lower-level subsystems, which are generated from the above mentioned basic
subsystem by replacement of one of the rows by any other row of the system (2)
which is not included in
12
, ,...,
M
Sk k k
:
12 1
12
, ,..., , ,
, ,..., : 1, , , , 1, 1,
,1,.
M
aa a
Mi ij
p
Sk k k l
Sk k k a M a a ij M i j
lk p M
(8)
Finding the most conformed set of estimates
ˆ
and the corresponding estimate
12
, ,...,
M
Sk k k
leads to the minimization of the measure of conformity among all
the subsystems
12
12 12 12
, ,..., 1,
ˆ
, ,..., : , ,..., arg min ( , ,..., )
M
ij
MM M
kk k N
kk
c ckk k kk k WSkk k
,
where
12
(,,...,)
M
WSk k k
is the measure of conformity for the subsystem
12
, ,...,
M
Sk k k
:
12 1
12 1
2
12 12
, ,..., ,
ˆˆ
, ,..., , ,..., , ,..., ,
M
aa a
M
MMaaa
Sk k k l
WSkk k ckk k ck k k l
,
and
12
ˆ
, ,...,
M
ck k k
is the estimate on the subsystem
12
( , ,..., )
M
Sk k k .
The described method of evaluation spares us storage of estimates on all the square
lower-level subsystems and reduces the number of comparisons, but this method
requires that the same solutions are repeatedly calculated. . Since any of
M
rows of
the subsystem can be replaced by one of
NM
rows, which are not in this
32

subsystem,
M
NM
subsystems are formed. Thus, each subsystem is calculated
1MN M
times that is redundant.
For the problem considered, the replacement of one row in a subsystem by a new
one comes to finding the intersection of the line corresponding to the remaining M-1
rows, and a hyperplane corresponding to added rows. As a result, the main
computational cost is connected with basic subsystems solving.
The number of inefficient computations can be reduced due to the use of a small
set of basic subsystems, which include every row of the initial system (2) only once.
The last variant of the solution is suitable for parallel implementation on
multiprocessor systems. In this case, the most conformed subset of the estimates can
be studied for on each set of the lower-level subsystems associated with one of the
basic subsystems. Then, by comparing the functions of mutual closeness of the
estimates obtained for different subsets and comparing their corresponding line
numbers, the most conformed set of the subsystems can be found.
4 Outcome of the Experiment
Comparative experimental studies of the conformed identification method and the
RANSAC algorithm were conducted in order to compare their accuracy in the same
operating conditions. The experiments were carried out on the data sets that were
modeled as follows.
In various systems (2) M = 8 and N = 12 or N = 16. The components of the
parameter vector
c were specified as uniformly distributed random numbers in the
range of 1 to 10. The elements of matrix X were calculated in accordance with (2) the
corresponding points coordinates, which are modeled as random sequences with given
variances.
Components of the error vector were formed in such a manner that the normal error
signal-to-noise ratio was in the range of 40-60 dB. For rough errors signal-to-noise
ratio was specified in the range of 0-10 dB.
In the most models described in the papers dedicated to the effectiveness of
RANSAC, the number of observations N significantly exceeds (by 2-3 orders of
magnitude) the number of the estimated parameters M. If the intensity of the noise is
reasonable, traditional statistical processing schemes give good results. Therefore, if
the number of degrees of freedom is great, the goal of most studies is to show the
advantages of the RANSAC in case when the number of rough errors reaches 80-90%
of the total number of observations.
In this paper, we consider the case when the number of observations N is usually
slightly higher than M (not more than 2-3 times). In this case, the statistical schemes
are not suitable. Also, the frequency of the anomalous error was specified more
realistically: 50-60% of the number of degrees of freedom (N-M) of the resulting
system.
For comparative evaluation of the accuracy and reliability of the algorithm, we
used the following parameters: the identification is correct if the ratio of the error
vector norm to the parameter vector norm does not exceed 0.3.
33
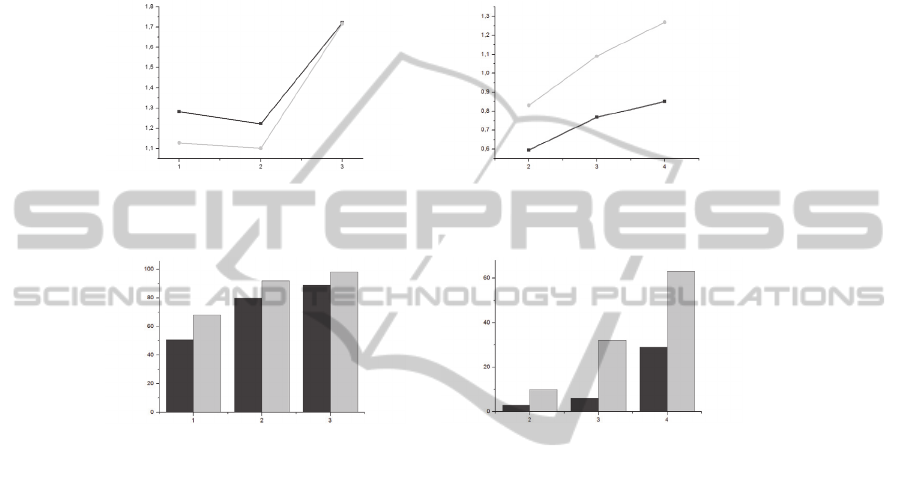
Figure 2 shows a plot of the mean values of the error on the number of correct
identifications of anomalous errors for different values of the number of estimated
parameters (light - for the method of RANSAC, dark - for the conformed
identification method). Figure 3 shows graphs illustrating the number of false
identifications to 100 experiments on the number of rough errors for the same values
of the estimated parameters. It is obvious that in all implementations, the conformed
identification method shows better results both in reliability and accuracy.
а) b)
Fig. 2. Mean error of the correct identifications: а) N=12, M=8; b) N=16, M=8.
а) b)
Fig. 3. The number of false identifications for 100 experiments: а) N=12, M=8; b) N=16, M=8.
3D scene stereo images from two cameras were obtained by using the POV-Ray
program. The cameras’ internal (camera matrices
1
K ,
2
K ) and external (rotation
matrices
1
R ,
2
R and translation vectors
1
C ,
2
C ) parameters [8] take the following
values :
12
400 0 400
0 400 300
001
KK
,
1
0,999048 0 -0,0436194
0,0308436 0,707107 0,706434
0,0308436 -0,707107 0,706434
R
,
2
0,999048 0 0,0436194
-0,0308436 0,707107 0,706434
-0,0308436 -0,707107 0,706434
R
,
1
0,5
5
5
C
,
2
0,5
5
5
C
.
Then with the help of OpenCV library, 16 corresponding points were found. On
basis of these points the fundamental matrix was formed. From the received
fundamental matrix, projective transformation matrices for each of the images were
generated, and stereo rectification was done. The same procedure was carried out for
34

the exact fundamental matrix, obtained from the given internal and external camera
parameters. The exact (
F ) and estimated (
ˆ
F
) matrices are given below:
5
5
0 -1,25 10 -0,00125
-1,25 10 0 0,166954
-0,00125 -0,156954 1
F
,
65
56
2,8918 10 3,16982 10 -0,0164114
ˆ
-5,51261 10 5,70682 10 0,170538
0,012072 -0,162094 1
F
.
Figures 4 and 5 show the rectified stereo pairs with the epipolar lines obtained
from the experiment for the exact and the estimated fundamental matrices,
respectively.
Fig. 4. Stereo pair rectified from the exact matrix.
Fig. 5. Stereo pair rectified from the estimated fundamental matrix.
Disparity maps were formed from the transformed stereograms by means of
OpenCV. Figure 6 shows the maps for the exact and estimated fundamental matrices,
respectively.
5 Conclusions
The application of the conformed identification method allowed us to come to certain
conclusions. It is hence shown that:
35

a) b)
Fig. 6. Disparity map for: a) exact fundamental matrix, b) estimated fundamental matrix.
1. The accuracy and reliability of fundamental matrix identification significantly
affects the accuracy and reliability of the reconstruction of the object.
2.
It is possible to achieve much higher accuracy and reliability of 3D-scene
reconstruction by using the conformed identification method in comparison with
the RANSAC algorithm.
3.
The computational complexity of the considered modification of the conformed
identification method still remains higher than that of the RANSAC method.
Although a high computational complexity of this method causes dissatisfaction, in
practice there are situations when the problem of determining the parameters of the
model has to be solved as accurately as possible on the single, though perhaps
small and very noisy, data set. Fortunately, as it shown in this paper, when
implemented on a multiprocessor system, it is not a serious problem because this
algorithm has a high degree of parallelism.
Acknowledgements
This work was financially supported by the RFBR (grants # 11-07-12051, #12-07-
00581, #13-07-97000).
References
1. Graupe, D. (1978). Identification of systems. New York: Robert E. Kriger Publishing
Company Huntington.
2. Ljung, L. (1987). System Identification – Theory for the User. Prentice Hall, Englewood.
Cliffs, N.J.
3. Kalman, R.E. (1985). Noised systems identification. Advances of Mathematical Sciences, v.
40, issue 4(244).
4. Allen, D.M. (1971). The prediction sum of squares as a criterion for selecting predictor
variables. Technical Report 23, University of Kentucky.
5. Fischler, M. & Bolles R. (1981). Random Sample Consensus: A Paradigm for Model Fitting
with Applications to Image Analysis and Automated Cartography. Comm. Of the ACM 24,
381–395.
36

6. Torr, P.H.S. & Murray, D.W. (1997). The Development and Comparison of Robust Methods
for Estimating the Fundamental Matrix. International Journal of Computer Vision, 24, 271-
300.
7. Fursov, V. & Gavrilov, A. (2004). Conforming Identification of the Controlled Object.
Proceeding International Conference on Computing, Communications and Control
Technologies: CCCT’2004, 326-330.
8. Forsyth, D. & Ponce J. (2004). Computer Vision: A Modern Approach. Moscow:
“Williams” Publisher.
37
