
FouSE: An Android Tool to Help in the Teaching of Fourier Series
Expansions in Undergraduate Education
Manuel J. C. S. Reis
1
, Salviano Soares
1
, Sim˜ao Cardeal
2
, Raul Morais
3
, Emanuel Peres
3
and Paulo J. S. G. Ferreira
4
1
IEETA/Departamento de Engenharias, University of Tr´as-os-Montes e Alto Douro,
Apartado 1013, 5001-801 Vila Real, Portugal
2
Portugal Telecom Inovac¸˜ao, Rua Eng. Jos´e Ferreira Pinto Basto, 3810-106 Aveiro, Portugal
3
INESC-TEC/Departamento de Engenharias, University of Tr´as-os-Montes e Alto Douro,
Apartado 1013, 5001-801 Vila Real, Portugal
4
IEETA/Departamento de Electr´onica, Telecomunicac¸ ˜oes e Inform´atica, University of Aveiro, 3810-193 Aveiro, Portugal
Keywords:
Android Application, Fourier Series Expansions, Undergraduate Electrical Engineering Education.
Abstract:
This paper presents an Android application to help in the teaching of Fourier series expansions in undergrad-
uate Electrical Engineering. Consequently, it discusses the teaching of Fourier series concepts in connection
with undergraduate Electrical Engineering education; some of the basic Fourier series theory is briefly re-
viewed. The presented Android application has been found useful in this context. As expected, the application
has an easy-to-use, friendly interface, and can be viewed as a tool to help undergraduate students test and as-
sess the Fourier series expansions on a typical set of signals, whose analytical Fourier series coefficients were
found during the theoretical lectures. Additionally, some of its main characteristics include the ability for the
students to control the total approximation error and the number of terms/harmonics used in the expansion.
1 INTRODUCTION
Among the most important studied topics in under-
graduate Electrical Engineering education are Fourier
series expansions (and Fourier theory in general). As
a natural consequence, a large fraction of the sig-
nal processing and also mathematical literature is de-
voted to the teaching of Fourier series expansions
(and Fourier theory in general). Having a solid un-
derstanding on the most basic principles of Fourier
series expansions is of utmost importance, especially
when dealing with problems which fall, for example,
in the scope of multidimensional signal reconstruc-
tion, and which includes sampling theory, interpo-
lation, extrapolation, signal and image conditioning,
interactive image repair, deconvolution and other in-
verse problems, reconstruction in tomography, filter
design, and much more.
Moreover, Clark Quinn (2000, http://
www.linezine.com/2.1/features/cqmmwiyp.htm) de-
fines Mobile Learning (mLearning) as “eLearning
through mobile computational devices: Palms, Win-
dows CE machines, even your digital cell phone”.
Harris, (Harris, 2001), defines mLearning as the
intersection point between mobile computing and
eLearning, producing a learning experience anytime
and anywhere. mLearning is characterized by the
capacity of accessing learning resources from any-
where, at any time, with high search capacities, high
interaction, high support for an effective learning and
a constant valorization based on the performance. So,
one can see mLearning as an extension of eLearning,
but characterized by its capacity of being independent
in terms of space and time. The idea is to have small
devices capable of being linked to the net, easy
data input, and the ability to display high resolution
images and also (very) good sound capacities. Hence,
mLearning can benefit from all advantages of the
web added to mobile technologies. In summary, we
may say that mLearning relies on the utilization of
mobile technologies at the service of the processes
associated with teaching and learning. There is a
huge number of mobile applications that have been
recently developed with the aim of being used within
the mLearning context. For example, in (Holzinger
et al., 2012) the authors discuss the development of
smart adaptive user interfaces for mobile e-Business
applications, and the lessons learned. In (Mujacic
166
J. C. S. Reis M., Soares S., Cardeal S., Morais R., Peres E. and J. S. G. Ferreira P..
FouSE: An Android Tool to Help in the Teaching of Fourier Series Expansions in Undergraduate Education.
DOI: 10.5220/0004401101660171
In Proceedings of the 5th International Conference on Computer Supported Education (CSEDU-2013), pages 166-171
ISBN: 978-989-8565-53-2
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

et al., 2012), Modelling, Design, Development
and Evaluation of a Hypervideo Application for
Digital Systems Teaching is presented and discussed.
The process of life-long learning, in conjunction
with three different models for mobile/ubiquitous
applications is discussed in (Holzinger et al., 2010).
We believe that a first course focusing on Fourier
series expansions would gratefully benefit from the
fact of having a tool that let students test and assess
Fourier series expansions, anytime and anywhere they
want, and using their own Android powered devices
(for example, during the lunch time conversations, us-
ing their own smartphones and tablets). Moreover,
this application can be a welcome addition to the
background of Electrical Engineering students, espe-
cially to those interested in telecommunications, in-
formation theory, or signal/ image processing in gen-
eral.
Solving problems while experimenting and com-
paring the available algorithms is of fundamental im-
portance in the learning process. The application pre-
sented in this paper was aimed at helping students do
that.
Additionally, we felt a need for tools that could be
easily used inside or outside the classroom, easily up-
dated and/or maintained, and that the students could
use with their own smartphones/tablets.
The development of the type of application proposed
and described here is additionally justified by the
increasing number of available mobile devices with
the required functionalities and capacities, described
above, and the number of students using them.
We believe that a small introduction to Fourier se-
ries will help to clarify the ideas that lead to the de-
velopment of the application. The next section is ded-
icated to this.
2 FOURIER SERIES DEFINITION
A signal (function) s(t) is said to have period T if
s(t +T) = s(t) for all t. If the signal is piecewise con-
tinuous in a period, with finitely many points of dis-
continuity and finitely many maxima or minima (also
known as Dirichlet’s conditions), then the Fourier se-
ries converges to (s(t+)+ s(t−))/2 (see, for example
(Tolstov, 1976), for details on existence and conver-
gence of the Fourier series). In that case, the Fourier
series of the signal s(t) is given by
s(t) = A
0
+
∞
∑
n=1
A
n
cos(nω
0
t) +
∞
∑
n=1
B
n
sin(nω
0
t),
with
A
0
=
1
T
Z
+
T
2
−
T
2
s(t)dt,
A
n
=
2
T
Z
+
T
2
−
T
2
s(t)cos(nω
0
t)dt
and
B
n
=
2
T
Z
+
T
2
−
T
2
s(t)sin(nω
0
t)dt,
where ω
0
= 2π f , and f =
1
T
, the fundamental fre-
quency of s(t).
Fourier series may come in different flavors and
tastes. Here, we are interested in the different con-
nections and interpretations it may have from a future
electrical engineer point of view. For example, see
chapter 5 of (Brigham, 1974) or (Ambardar, 1995) for
the connections between the complex and trigonomet-
ric forms of the Fourier series, the Fourier series as a
special case of the Fourier integral, waveform sam-
pling, and sampling theorems.
2.1 Fourier Series of Even, Odd and
Half-wave Symmetric Signals
The Fourier series expansion of an even signal s
e
(t)
with the period of T does not involve the terms with
sin and has the form
s
e
(t) = A
0
+
∞
∑
n=1
A
n
cos(nω
0
t),
where the Fourier coefficients are given by
A
0
=
2
T
Z
+
T
2
0
s
e
(t)dt,
and
A
n
=
4
T
Z
+
T
2
0
s
e
(t)cos(nω
0
t)dt.
Accordingly, the Fourier series expansion of an odd
T-periodic signal s
o
(t) consists of sine terms only and
has the form
s
o
(t) =
∞
∑
n=1
B
n
sin(nω
0
t),
where the coefficients B
n
are
B
n
=
4
T
Z
+
T
2
0
s
o
(t)sin(nω
0
t)dt.
A T-periodic signal s
h
(t) is said to have half-wave
symmetry if s
h
(t ±
T
2
) = −s
h
(t). In that case, the
Fourier series expansion coefficients will be
A
0
= 0,
FouSE:AnAndroidTooltoHelpintheTeachingofFourierSeriesExpansionsinUndergraduateEducation
167
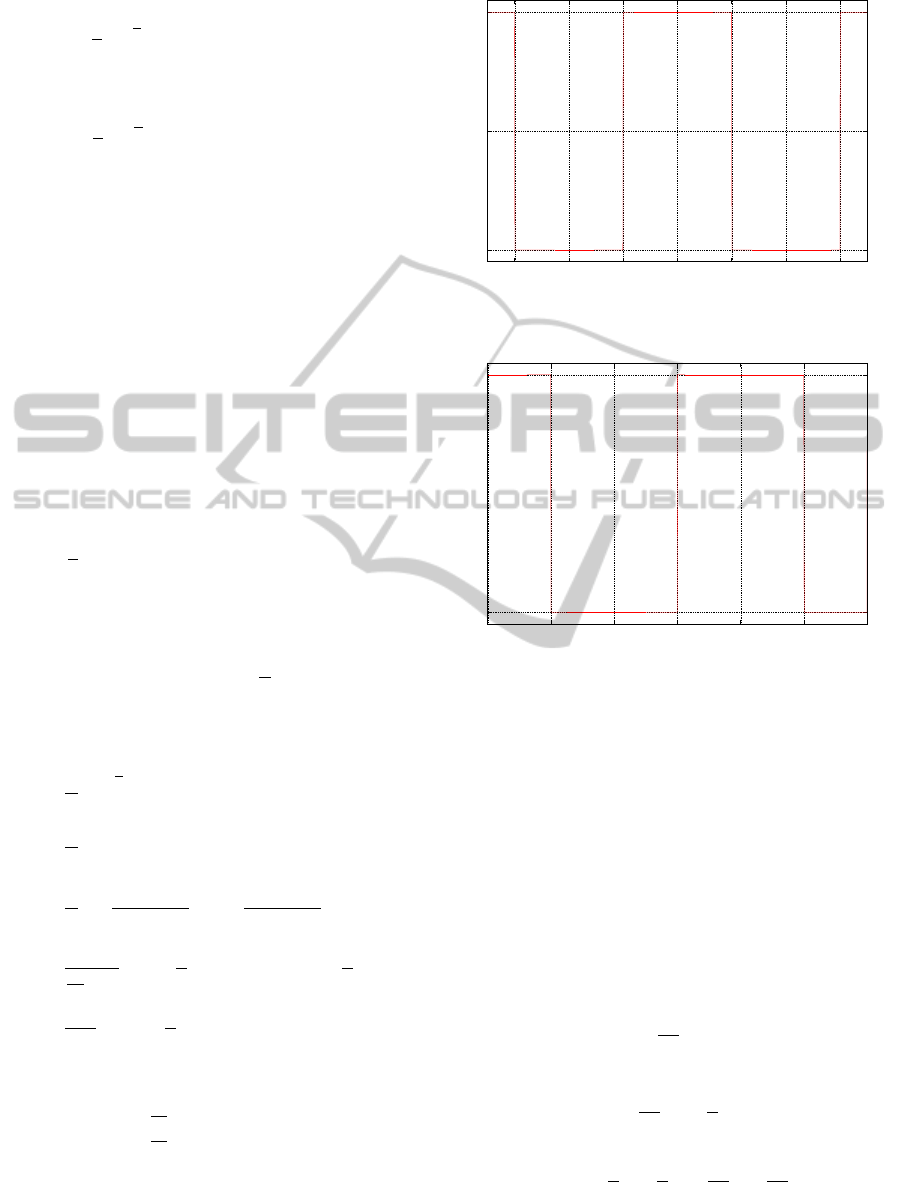
A
n
=
(
0, n even,
4
T
R
+
T
2
0
s
h
(t)cos(nω
0
t)dt, n odd,
and
B
n
=
(
0, n even,
4
T
R
+
T
2
0
s
h
(t)sin(nω
0
t)dt, n odd.
2.2 A Typical Example—Square Wave
The next example shows a typical calculation of the
Fourier series expansion coefficients, that we usually
solve during the theoretical-practical lessons.
Let the periodic signal s(t) be defined by
s(t) =
−1, −2 < t < −1,
1, −1 < t < 1,
−1, 1 < t < 2.
(1)
Typically, to find the coefficients of its Fourier series
expansion we begin by plotting the signal, like the one
presented in figure 1. From this figure (or from equa-
tion 1) we can easily find that the period is T = 4,
leading to ω
0
= 2π/T = π/2, and that s(t) = −s(t),
leading to B
n
= 0. Additionally, we may also note
that s(t +
T
2
) = −s(t) (half-wave symmetry), leading
to A
n
= 0 for all n even. In conclusion, we only need
to find the coefficients A
n
for n odd, and so the Fourier
series expansion will be of the form
s(t) =
∞
∑
n=1
n odd
A
n
cos(n
π
2
t).
By the definition above,
A
n
=
4
T
Z
+
T
2
0
s(t)cos(nω
0
t)dt,
=
4
T
Z
1
0
cos(nω
0
t)dt +
Z
2
1
−cos(nω
0
t)dt
,
=
4
T
(
sin(nω
0
t)
nω
0
1
0
−
sin(nω
0
t)
nω
0
2
1
)
,
=
4
2π
ω
0
nω
0
h
sin(n
π
2
) − sin(nπ) + sin(n
π
2
)
i
,
=
4
2nπ
h
2sin(n
π
2
)
i
,
i.e.,
A
n
=
−
4
nπ
, n = 3,7,11, ·· · ,
4
nπ
, n = 1,5,9, ·· · .
Note that the signal plotted in figure 1 and the cor-
responding expansion coefficients are the same used
in the “square”-like wave form used in the available
signals of the application (also illustrated in figure 3).
-1
0
1
-3 -2 -1 0 1 2 3
s(t)
t
1
-1
1
-1
Figure 1: Plot of the square-like wave signal defined by
equation 1.
0
2
-3 -2 -1 0 1 2 3
s
s
(t)
t
1
-1
Figure 2: Result of shifting and translating by one the signal
presented in equation 1.
Now, suppose that we shift the signal up and trans-
late it right by one. The resulting signal, s
s
(t), is pre-
sented in figure 2. As a consequence, the signal will
no longer be even, and will also lose its half-wave
symmetry. A common mistake our students some-
times do is to assume that the translation of the sig-
nal converts it into an odd one, but the shift up also
removes this symmetry (despite of the signal shape,
which still is a square-like one). In this particular case
the new coefficients will be
A
0
= 1,
A
n
= 0,
B
n
=
8
nπ
, n odd.
This means that
s
s
(t) = 1+
∞
∑
n=1
n odd
8
nπ
sin(n
π
2
t),
= 1+
8
π
sin(
π
2
t) +
8
3π
sin(
3π
2
t) + ·· · .
This type of manipulations (translations and
shifts) are made so the students can gain some insight
CSEDU2013-5thInternationalConferenceonComputerSupportedEducation
168

on the changes introduced in the coefficients of the
Fourier series expansion, and actually realize that the
new values of the coefficients may become very dif-
ferent.
3 THE APPLICATION
The Android application, named “FouSE—Fourier
Series Expansions”, is freely available for download
from “Google Play” (www.google.com). Android
was our first choice, because the majority of our stu-
dents have Android powered devices; still, we want to
produce an iOS equivalent application. No particular
concerns have directed the design of the user inter-
face, besides the basic and obvious ones, and the ma-
jor guidelines, as discussed for example in (Holzinger
et al., 2012; Mujacic et al., 2012). Figure 3 shows a
screenshot of the application. When no signal is se-
lected, the spinner on the upper left corner will show
the word “none” and the plotting spaces of the origi-
nal and approximation signals, as well as the next har-
monic plot, will be empty, because they have nothing
to show.
The user interaction with the application is very
straightforward. The first thing a user must do is to
choose a signal from the list (by pressing the spinner
below the text “Signal”). Then, by simply pressing
the “Add” button, the user refines the approximation
to the desired accuracy.
The list of available signals include:
• Sawtooth;
• |sin| (full wave rectified);
• Half sin (half wave rectified);
• Square;
• Triangle;
• Parabolic (t
2
).
Figure 3: Fourier series expansion of a square-like wave:
DC term plus 6 harmonics.
The “control” section of the interface is placed on
the left side of the screen. As seen above, the spinner
below the word “Signal” is used to choose the signal
to approximate. Once a signal is chosen, more infor-
mation and control buttons will be visible. The error,
over a period, of the approximation is presented using
two different metrics:
• L
2
=
q
∑
N
i=1
(signal
i
− approximation
i
)
2
;
• L
∞
= max
i
|signal
i
− approximation
i
|.
The “Add” button is used to add the next term (the
signal presented next to this button and below the text
“Next harmonic”) to the approximation signal. The
“Reset” button restarts the approximation.
The upper right side of the screen presents two sig-
nals plots and one text message:
• the original signal plot (in white);
• the current approximation signal plot (in red);
• the number of terms used in the current approxi-
mation (DC term, plus harmonics, if any).
Every time the “Add” button is pressed, the cur-
rent harmonic plotted below the text “Next harmonic”
is added to the current approximation, a new har-
monic is presented here replacing the previous one,
the approximation signal is re-plotted, the new errors
are computed, and the number of terms used in the
current approximation is updated in the text message
next to the main graph.
Figure 3 shows an example of an approximation.
In this case, the original signal is a square-like wave,
plotted in white, and the result of the approximation,
after summing the DC component plus six harmon-
ics/terms of the Fourier series expansion, is plotted
in red, over the same graph. On the graph below,
it is presented the plot of the next harmonic/term to
be added to the result of the approximation plotted in
red, if the “Add” button is pressed. The current er-
ror of the approximation over a period is also shown
(L
2
= 132.3553 and L
∞
= 52.5), and it will decrease
if more harmonics/terms are added to the approxima-
tion.
Note that the scales (and axes) used for the signals
and harmonic plots are different, and automatically
adapt from expansion to expansion. However, these
scales remain constant during a particular expansion,
so the student can realize the different weights that
successive harmonics will have in the approxima-
tion. For example, figure 4 shows the result of the
Fourier series approximation to a square-like wave,
after using the DC term plus 18 harmonics. When
compared to figure 3 we may note the big difference
in the weights of harmonic number 7 and harmonic
number 19 (obviously, the same applies to the error
FouSE:AnAndroidTooltoHelpintheTeachingofFourierSeriesExpansionsinUndergraduateEducation
169
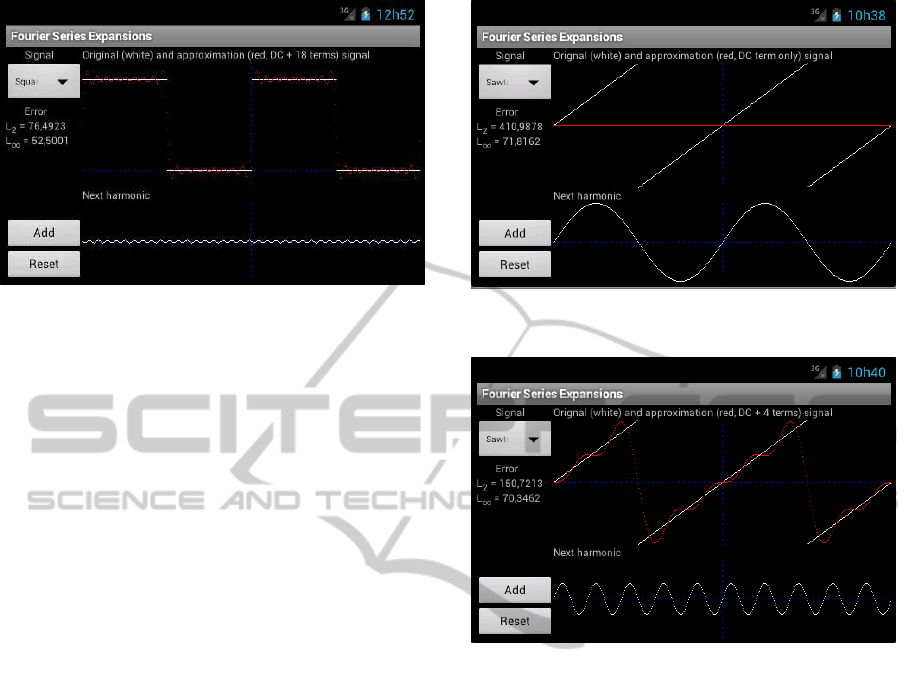
Figure 4: Fourier series expansion of a square-like wave:
DC term plus 18 harmonics.
L
2
= 76.4923 and L
∞
= 52.5001). Note that, in this
case, L
∞
error remains constant (52.5); this is due
to the Gibbs phenomenon (see, for example, (Jerri,
2011) for details).
Figures 5 and 6 show the Fourier series expansion
approximation to a sawtooth-like wave. In figure 5
it is used the DC term only to the approximation (all
the approximations start with the DC term only). It is
well visible that, in this case, DC = 0 and so it over-
laps the t (time) axis in the plot. Also note the first
harmonic term was scaled to completely fill the plot-
ting area reserved to the plot of the harmonics. Now,
from figure 6 we can see that the fifth harmonic term
will have a much lower weight in the series final re-
sult. Note also that the time axis is now well visible in
the approximation plot; as stated above, when the ap-
proximation started the null DC term overlapped the
time axis.
A help menu is also available, by pressing the
“menu” button of the smartphone/tablet.
4 SOME RESULTS
We have distributed a copy of the application directly
to our students, i.e., the students installed the appli-
cation directly on their devices without the need of
downloading it from “Google Play”, after the subject
was taught in class.
We have anonymously surveyed our students with
the following questions:
1. Gender.
2. Do you consider that the application has an ease
to use interface?
3. Have you ever used or needed to use the help
menu?
Figure 5: Fourier series expansion of a sawtooth-like wave:
DC term only.
Figure 6: Fourier series expansion of a sawtooth-like wave:
DC term plus four harmonics.
4. Do you prefer a web-based tool (applet) or this
(android) version? Please tell us why.
5. Do you think that the application matches/covers
the contents taught related to the Fourier series?
6. Do you think this application helped you in under-
standing the Fourier series (basics, how it works
and its applicability)?
7. Do you think this application helped you in un-
derstanding other topics/subjects in this or other
courses?
8. Do you think it would be beneficial to have similar
tools in other subjects & courses?
In a total of 85 enrolled students, 55 completed the
survey, from which 50 (91%) were males and 5 (9%)
females. 51 (93%) of the surveyed students consider
that the application has an ease to use interface, and
only 4 (7%) found it somehow difficult or hard to use.
However, only 2 (4%) of the total responding students
have tried the help menu; curiously, these students are
two of the four considering the application hard or dif-
ficult to use.
From the responding students, 47 (85%) prefer
CSEDU2013-5thInternationalConferenceonComputerSupportedEducation
170

this android version, when compared to other web-
based applications (applet like) available on the Inter-
net. When asked why, they answered that this appli-
cation “is really portable (in the sense that we don’t
need to be always connected; we can do simulations
even if we do not have Internet access)” and “it seems
that the interface was designed and developed to ex-
tract the maximum from my android device, in con-
trast to a web-based applet were we constantly need to
adjust the screen size, resolution, among other”. The
other 8 (15%) students consider the web-based (ap-
plet) version more suited to their needs: “don’t like
to install apps” and “web-based applications are re-
ally platform independent” were the two main reasons
presented for that. In this group we also counted the
iOS (iPhone/iPad) users, who revealed that they are
willing for an iOS version of the tool.
A total of 53 (96%) of the responding students
consider that the tool matches/covers the subjects
studied within the Fourier series topics, and 54 (98%)
believe that it helped them in understandingthe basics
of the Fourier series, how it works and its applicabil-
ity. In addition, 50 (91%) students consider that this
tool helped them to understand other topics under this
course and even in other courses. The referred top-
ics include: some signals’ properties (like symmetry,
frequency, etc.); Fourier transform; math series con-
struction; and programming (the code of the applica-
tion was made available to our students).
When asked if other courses/topics/subjects
should benefit from similar tools/applications the an-
swer was the answer was unanimous (100% (55) of
the responding students said yes).
5 CONCLUSIONS
Fourier series expansions are among the problems
that an electrical engineer most often faces. An un-
dergraduate course in the subject not only provides
the student with relevant know-how concerning the
problems, but may also be of considerable value in
understanding how a background in Fourier and nu-
merical analysis can be applied in the field, to con-
crete engineering problems.
In this context, we felt a need for tools that could
be easily used inside or outside the classroom, in for-
mal and informal contexts, and at the same time were
easy to update and maintain. The application that
we have described allows the student to try several
Fourier series expansions on a set of typical signals,
and then compare the results in an easy-to-use envi-
ronment, and using their own Android powered de-
vices.
The application, named “FouSE—Fourier Series
Expansions”, is freely available for download from
“Google Play” (www.google.com), and can be used
by the students in their daily work, inside or outside
the classroom, and have proved to be a valuable tool
for teaching and understanding Fourier series expan-
sions.
ACKNOWLEDGEMENTS
This work was partially supported by Portugal Tele-
com Inovac¸˜ao in the context of Project e-VoIP.
REFERENCES
Ambardar, A. (1995). Analog and digital signal processing.
PWS Publishing Company, Boston, MA.
Brigham, E. O. (1974). The Fast Fourier Transform.
Prentice-Hall, Englewood Cliffs, NJ.
Harris, P. (2001). Going mobile. Learning Circuits. ASTD
Online Magazine. http://www.astd.org/.
Holzinger, A., Geier, M., and Germanakos, P. (2012). On
the development of smart adaptive user interfaces for
mobile e-Business applications: Towards enhancing
user experience — some lessons learned. In Proceed-
ings of the International Conference on e-Business
(ICE-B), pages 3–16, Rome, Italy.
Holzinger, A., Nischelwitzer, A., Friedl, S., and Hu, B.
(2010). Towards life long learning: Three models
for ubiquitous applications. Wireless Communications
and Mobile Computing, (10):1350–1365.
Jerri, A. J., editor (2011). Advances in the Gibbs Phe-
nomenon. Sampling Publishing.
Mujacic, S., Debevc, M., Kosec, P., Bloice, M. D., and
Holzinger, A. (2012). Modelling, design, develop-
ment and evaluation of a hypervideo application for
digital systems teaching. Multimedia Tools and Ap-
plications, (2):435–452.
Tolstov, G. P., editor (1976). Fourier Series. Dover Publi-
cations Inc., N.Y.
FouSE:AnAndroidTooltoHelpintheTeachingofFourierSeriesExpansionsinUndergraduateEducation
171
