
A Hybrid Control System for a Tentacle Arm
Nirvana Popescu
1
, Decebal Popescu
1
and Mircea Ivanescu
2
1
Computer Science Department, University Politehnica Bucharest, 365 Independent Avenue, Bucharest, Romania
2
Department of Mechatronics, University of Craiova, 13, Cuza street, Craiova, Romania
Keywords: Tentacle, Weighted Error, Boundary Control.
Abstract: The paper studies the control problem of a class of light- hyper-redundant robots, a tentacle arm, described
by hyperbolic Partial Differential Equations with uncertain components. The stability analysis and the
resulting controllers are obtained using the concept of boundary geometric control and a spatial weighted
error control technique. A hybrid controller with two control components: a PD boundary control and a
pneumatic system that controls the locking forces in the joints are discussed. Liapunov techniques are used
to prove the control system stability. Numerical simulations and experimental results are also provided to
verify the effectiveness of the presented approach.
1 INTRODUCTION
This paper implements a control system for a class
of hyper-redundant robots, a tentacle model. The
tentacle robots represent one of the most attractive
domains of robotics during the last decade. A great
deal of research has been conducted using this type
of robot and environmental structure. In (Chirikjian,
1990); (Robinson, 1999); (Gravagne, 2000), the
kinematic models were analysed. In (Mochiyama,
1999), the problem of controlling the shape of a
robot with two-degree-of-freedom joints was also
investigated using spatial curves. A controller for
continuum robots was developed by (Braganza
,
2007)
. Other researchers derived a new kinematic
model by using the differential geometry (Walker,
1999) or introduced a real-time controller for
continuum robots (Jones, 2006). In (Kapadia, 2009)
it was proposed a sliding controller for extensible
robots. The control problem of a class of continuum
arms that performs the grasping function by coiling
is also discussed in (Ivanescu, 2008). A frequency
stability criterion for the grasping control problem is
advanced in (Ivanescu, 2010). Several biomimetic
robotic prototypes have been developed in (La
Spina, 2007);
(KeJun, 2010) and continuum robots
with multiple, concentric, elastic tubes were
analysed and discussed in (Rucker, 2010); (Bailly,
2011). All these research works underline the
complexity of control problems, the difficulty in
implementing feedback controllers and
compensators determined by the dynamic models
expressed by partial differential equations (PDE)
and by the observability problems in distributed
parameter systems. Controller design for these
systems is in general based on an approximated
finite –dimensional model, by truncating the infinite
number of modes and by neglecting the higher
frequency modes and by geometric control
(Christofides, 1996); (Shang, 2005); (Maidi, 2009);
(Maidi, 2010).
Our paper treats the control problem of a class of
light tentacle robots. The dynamic model of the arm
is described by hyperbolic Partial Differential
Equations (PDE) with uncertain components. By
using a spatial weighted error control, the infinite
dimensional system control becomes a finite
dimensional control problem. A robust algorithm
with the characteristics of the conventional PD
control is proposed. The stability of the system with
the respect of weighted error is proven. The paper is
structured as follows: section II presents
technological model, section III analyses the
mathematical model, section IV treats the control
problem, section V verifies the control laws by
computer simulation, section VI presents the
experimental results and section VII is concerned
with conclusions.
2 TECHNOLOGICAL MODEL
The technological model basis is a light weight arm.
Although the conventional hyper-redundant models
50
Popescu N., Popescu D. and Ivanescu M..
A Hybrid Control System for a Tentacle Arm.
DOI: 10.5220/0004403200500057
In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2013), pages 50-57
ISBN: 978-989-8565-70-9
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

operate in 3-D space, the motion control will be first
inferred from the planar models. The 2D model basis
from Fig 1 consists of a chain of vertebrae with a
backbone type structure. All the joints of the arm are
passive. The driving system of this arm has two
components: a DC motor system with cable-tendons
ensures the main motion of the arm and a pneumatic
system controls the locking forces in the joints.
Because the cables do not drive every element,
externally attached springs between elements are
introduced. The high flexibility of the arm is
obtained by these rotational joints associated with
the springs, distributed along the arm. The elements
of the arm are clustered in segments, each segment
having its own pneumatic control system. The
pneumatic driven system is composed by a single
acting mini-cylinder that develops a variable friction
force in the i-joint. For high value of these forces, all
the segment joints can be locked. We define this
case as “the cluster segment (CS) is locked”. If the
elements of a CS are locked, the locked joints will
not be rotatable and the cluster position is kept. The
tendon driving system will rotate only the unlocked
joints (Popescu, 2013).
The essence of the arm is the backbone curve C
(Fig 2). The independent parameter is related to
the arc-length from origin of the curve C,∈
Ω,Ω
0,
, where is the length of the arm. We
denote by the slope of the curve, = is the
generalized coordinate. Also, represents the
equivalent moment at the end of the arm
exercised by the cable forces
. The arm can be
assimilated with an ideal hyper-redundant arm, with
a distributed mass and damping , with the mass
density , the elastic modulus , the moment of
inertia and the rotational inertial density
.The
position measuring of a cluster segment is obtained
by electro-active polymer sensors that are placed on
the surface of each segment.
Figure 1: The 2D technological arm.
Figure 2: The ideal arm.
The sensors can measure the coordinate , at
the location ∈Ω
,Ω
∁Ω , where Ω
denotes the
domain of permissible sensor locations.
3 MATHEMATICAL MODEL
The dynamic model can be expressed by the
following Partial Differential Equation (PDE)
(Gravagne, 2000),
where
,
,∈Γ
Ω
∁
Ω
,Ω
|
∈
0,
,=
⁄
,
is the rotational inertial
density, is the arm bending stiffness, b is the
equivalent damping coefficient of the arm,
characterizes the elastic behaviour and defines the
nonlinear gravitational term. We assume the
following initial and boundary conditions
0,
,0
0,
,
where is the equivalent moment generated by the
cable forces. In (1), the friction is modelled using the
viscous component and neglecting the Coulomb
and static friction (Qing, 2006),
where
is the coefficient of joint geometry and
is the viscous coefficient. The state of the system is
defined by the vector
∈Γ∁
Ω
Ω
.
The input is represented by the moment
at the
boundary of the arm. For the gravitational term
,, that is difficult to be evaluated in a complex
motion, we consider that the following constraint is
verified ( Khopalov, 2010)
‖
.,
‖
‖
.,
‖
AHybridControlSystemforaTentacleArm
51

where M is a positive constant. We consider a
desired state
,
∈
0,, that satisfies (1)
with boundary conditions (3) and we denote by
,
,
the distributed error variable,∈
0,
.
Definition 1 (Popescu, 2013). The Weighted Error
with respect to a sensor
, (
W-Error), is
the spatial weighted value of the distributed error
variable (6),
̃
,
,
,
̃
where ,
is the spatial weighting function that
satisfies the following equation
,
Λ
,
with boundary conditions
0,
0,
,
01,2,…,
where Λ
is a positive constant. We chose a solution
of (8)-(9) as
lim
→
,
0
where
,1,2,.., are the eigenfunctions of
the Sturm-Liouville problem
0
0,
0
Figure 3: The weighting function,
,
.
,
sin
,∈Ω
,
0, ∈Ω
(13)
where Ω
2
,
represents the sensor
position, is the magnitude and defines the
function characteristic (Fig 3). This function verifies
the boundary conditions (9) and the set
,
1,2,..,
forms a complete set. So we can use the
approximation
,
∑
0
(14)
where
,
can be obtained from (11) - (12) as
21
2
1
,1,2,….,,
The boundary conditions (8) are satisfied by
and the constant Λ
can be evaluated from (8) and
(14).
4 CONTROL
4.1 Control System
The control problem consists of finding the control
law
such that the
W-Error (7) converges to
zero.
Definition 2. The W-Error control system is stable if
lim
→
̃
0
In terms of this definition we can synthesize a PD -
W-Error controller that guarantees stability in the
closed loop system.
Theorem 1. A
W -Error control of the system (1)-
(3) is stable (in the sense of Definition 2) if the
control law is
∆
1
∑
0
0
,0
,
,
(17)
where
,
are the control coefficients, that verify
the conditions:
0,
0
∝
∝Λ
∝
∝
∝
0
(18)
∆
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
52

and
is the desired moment applied at .
Proof. See Appendix.
4.2 Control Strategy
The control system is presented in Fig 4. It is a
hybrid driving system that controls the cable motors
and pneumatic system in order to ensure sequential
locked or unlocked cluster segments. The desired
trajectory is obtained sequentially by concatenation
of the locked or unlocked cluster segment effects.
Let (
,
,
..
be the desired
trajectory defined by the position sensors along each
cluster segment .
Figure 4: Control system.
Step 1. The position sensor,
associated to the first CS, is activated (the desired
position
. The control algorithm (17)-(19) is
applied at the cable driving system. All arm is
bending (Fig 5a).
Step 2. When ̃
0, the pneumatic control is
activated and the CS 1 is locked.
Step 3. The position sensor,
associated to the second CS, is activated (the
desired position
.
(a) (b)
(c)
Figure 5: Control strategy.
The control algorithm (17)-(19) is applied at the
cable driving system (Fig 5b).
Step 4. When ̃
0, the pneumatic control is
activated and the CS 2 is locked.
Step 5. The procedure is repeated for the cluster
segments 3, 4… N.
Consequently, we can control the arm motion,
sequentially, step-by-step, by altering the locked and
unlocked CS configuration. The whole procedure for
an arm with three cluster segments is shown in
Figure 5.
5 NUMERICAL SIMULATION
Consider the dynamic model of a tentacle robotic
arm described by (1) where the length of the arm
is1, the rotational inertial density is
0.001 kg m
2
, the bending stiffness15, the
viscous coefficient is 12/ and the
elastic coefficient is 1.5. These constants are
scaled to realistic ratios for a long thin arm. The
initial and boundary conditions are:
0 ,
,00;
,, where is the torque
applied at the top of the arm . The uncertain
term h(t, s) defines the gravitational components,
sin
, where is the linear
density, g is gravitational acceleration and A is the
section area. For the characteristic values of these
parameters (0.8
⁄
,10
⁄
,
410
), associated to this thin long arm, the
inequality (5) is satisfied for M = 2. The arm
contains two equal cluster segments.
A spatial weighting function (13) is selected for
0.4,
0.9 and an approximation (14)
with K=100 is used. The constants Λ
4.5 and
Λ
6.8 are determined. A control law (17) with
0.2,
4,
20 is implemented. These
coefficients verify the stability conditions (18).
Step 1. The desired state is
1.8cos1.5
and represents the objective of the first stage. The
arm (both segments) is bending to the desired
position (as in Fig 5a). The position sensor
is used
for position control. The control law (17) with
is implemented. The dynamic of the
distributed error , is presented in Fig 6.
Step 2. When ̃
0, the pneumatic control is
activated and CS 1 is locked.
Step 3. A desired state for the 2
nd
segment
1.8cos
1.5
is imposed. The position sensor
is used for position control. The control law (17)
AHybridControlSystemforaTentacleArm
53

with
is implemented. The dynamic of the
distributed error , is presented in Fig 7.
Figure 6: Error dynamics, e(t, s)- Cluster Segment 1.
Figure 7: Error dynamics, e(t, s)- Cluster Segment 2.
We remark that the 1
st
CS is locked, the
distributed error is
,
0,∈0,
and the
control position is obtained for the 2
nd
CS, ∈
,,
(Fig 5b).
Step 4. When ̃
0, the pneumatic control is
activated and CS 2 is locked. The good
performances of the proposed control algorithm can
be concluded from the graphics.
5 EXPERIMENTAL RESULTS
In order to verify the suitability of the control
algorithm, a platform with a 2D tentacle arm has
been employed for testing. The arm consists of two
cluster segments, each segment having six links
serially connected by revolute joints in a chain. All
the joints are passive. A pair of antagonistic cable
actuators connected at the terminal point = 0.4
m ensures the actuation system. The force in each
cable is determined by the DC motors and a
transmission system. The “state of locking” of each
joint is obtained by a pneumatic mini-linear actuator.
A polymer thick film layer is placed on the upper
element of each segment. A sensor exhibits a
decrease in resistance when an increase of the film
curvature is used. A Wheatstone bridge system is
used to measure the variation of the resistance. The
arm in the initial position, a vertical one is shown in
Fig. 8.
Figure 8: The arm positions.
Figure 9: Tracking position- Cluster Sensor1.
A Quanser based platform is used for control and
signal acquisition. A control law (17) with
1.8cos
1.5
is implemented. The new positions of
the arm after steps 1 and 2 are presented in Fig. 8.
The sensor information on the first segment is
shown in Fig. 9.
Now, the cluster segment 1 is locked and a new
actuation is obtained by bending the segment 2 for a
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
54
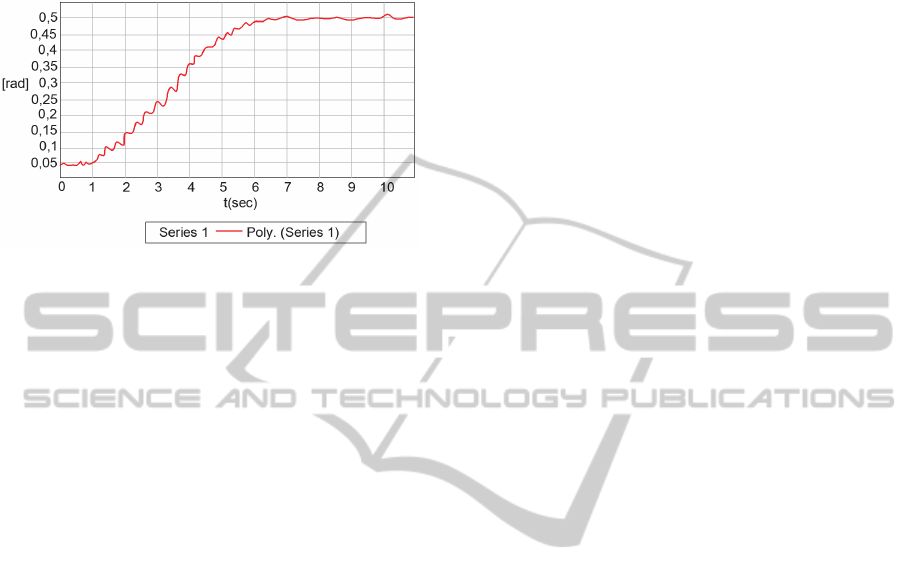
new desired position
2.7cos
1.5
. This
position is illustrated in Fig 8 and the sensor data are
presented in Fig 10. An analyse of this experimental
result confirms the algorithm performance.
Figure 10: Tracking position- Cluster Sensor2.
6 CONCLUSIONS
In this paper, the control problem that is related to a
class of tentacle arms has been discussed. The model
basis consists of a chain of vertebrae periodically
spaced, each element having a special joint that
ensures the rotation, elastic contact and a
controllable friction force with the following
element. All the joints are passive. We propose a
hybrid controller with two control components: a PD
boundary control and a pneumatic system that
controls the locking forces in the joints. For the
dynamic model described by a hyperbolic PDE with
uncertain components, a robust algorithm based a
spatial weighted error technique is discussed.
Liapunov methodes are used to prove the control
system stability. Numerical simulations and
experimental results verify the effectiveness of the
presented algorithms and techniques.
ACKNOWLEDGEMENTS
This work has been supported by PPCA 150/2012
Romania.
REFERENCES
Robinson ,G., Davies, G. B. C., 1999 “Continuum Robots
– A state of the art”, Proc. IEEE Int. Conf. on Robotics
and Automation, Detroit, May 1999, pp. 2849 – 2854.
Gravagne, Ian A., Walker, Ian D., 2000, On the kinematics
of remotely - actuated continuum robots, Proc. 2000
IEEE Int. Conf. on Robotics and Automation, San
Francisco, April 2000, pp. 2544-2550.
Gravagne, Ian A., Walker, 2000 Ian D., Kinematic
Transformations for Remotely-Actuated Planar
Continuum Robots, Proc. 2000 IEEE Int. Conf. on
Rob. and Aut., San Francisco, April 2000, pp. 19-26.
Chirikjian, G. S., Burdick, J. W., 1990, An obstacle
avoidance algorithm for hyper-redundant mani-
pulators, Proc. IEEE Int. Conf. on Robotics and
Automation, Cincinnati, Ohio, May 1990, pp. 625 – 631.
Mochiyama , H., Kobayashi, H., 1999, The shape Jacobian
of a manipulator with hyper degrees of freedom, Proc.
1999 IEEE Int. Conf. on Robotics and Automation,
Detroit, May 1999, pp. 2837- 2842.
Braganza, D., D. M. Dawson, Walker, N. Nath, N., 2007,
“A neural network controller for continuum robots”,
IEEE Transaction Robotics, vol. 23, issue 6, Dec.
2007, pp. 1270 – 1277.
Walker, I., M. Hannan, M., 1999, “A novel elephant’s
trunk robot”, AIM ’99, pp. 410 – 415.
Jones, B., I. D. Walker, 2006, “Practical kinematics for
real-time implementation of continuum robots”, IEEE
Trans. Robotics, vol. 22, no. 6, Dec. 2006, pp. 1087 –
1099.
Kapadia, I. Walker, D. Dawson, 2009 “A model – based
sliding mode Controller for Extensible Continuum
robots”, Recent Advances in Signal Processing,
Robotics and Automation, ISPRA Conf., 2009, pp. 103
– 120.
Ivanescu, M., Florescu, M. C., Popescu, N., Popescu,
D.,2008, Position and Force Control of the Grasping
Function for a Hyperredundant Arm, Proc. of IEEE
Int. Conf. on Rob. and Aut., Pasadena, California,
2008, pp. 2599-2604.
Ivanescu, M., Bizdoaca, N., Florescu, M., Popescu,N.,
Popescu, D.,2010, Frequency Criteria for the Grasping
Control of a Hyper-redundant Robot, Proc.of IEEE
International Conference on Robotics and
Automation, Anchorage, Alaska (ICRA 2010), May 3
– 8, 2010, pp. 1542-1549.
Ivanescu , M., D. Cojocaru, N. Bizdoaca, M. Florescu, N.
Popescu, D. Popescu, S. Dumitru,2010, “Boundary
control by boundary observer for hyper-redundant
robots”, Int. Journal of Computers, Communications
and Control, 2010, pp. 755 – 767.
G. La Spina, M. Sfakiotakis, D. Tsakiris, A. Memciassi, P.
Dario,2007, Polychaete-Like Undulatory Robotic
Locomotion in Unstructured Substrates, IEEE Trans
on Robotics, vol 23,No 6,Febr 2007, pp1200-1212
KeJun Ning, F.Worgotter, 2009, A Novel Concept for
Building a Hyper-Redundant Chain Robot, IEEE
Trans on Robotics, vol 25,No 6,Dec 2009, pp 1237-
1248.
Rucker, D. C., B. A. Jones, R. J. Webster III,2010, A
Geometrically Exact Model for Externally Loaded
Concentric-Tube Continuum Robots, IEEE Trans on
Robotics, vol 26,No 5,Oct 2010, pp769-780.
Bailly,Y., Y. Amirat, G. Fried, Modeling and Control of a
Continuum Style Microrobot for Endovascular
Surgery, IEEE Trans on Robotics, vol 27,No 5,Oct
201, pp 1024-1030.
AHybridControlSystemforaTentacleArm
55

Bajo, A., N. Simaan,2012, Kinematics-Based Detection
and Localization of Contacts along Multisegment
Continuum Robots, IEEE Trans on Robotics, vol
28,No 2,April 2012, pp 291-302.
Christofides, P. J., and P. Daoutidis,1996, Feedback
control of hyperbolic PDE systems. AIChE Journal,
42:3063 –3086, 1996.
Maidi, A., M. Diaf, and J. P. Corriou.2009, Boundary
geometric control of a heat equation. European
Control Conference (ECC’09), August 23-26, 2009,
Budapest, Hungary:4677–4682, 2009b.
Maidi, A., J. P.Corriou, Boundary Control of Nonlinear
Distributed Parameter Systems by Input-Output
Linearization.2011,18 th IFAC Congress, Milano,
August 228-30, 10910-10916.
Shang,H., J. F. Forbes, and M. Guay,2005, Feedback
control of hyperbolic distributed parameter systems.
Chemical Engineering Science, 60:969 – 980, 2005.
Maidi, A., J. P.Corriou, 2011, Boundary Control of
Nonlinear Distributed Parameter Systems by Input-
Output Linearization.18 th IFAC Congress, Milano,
August 228-30, 10910-10916.
Khopalov, A., 2010, “Source localization and sensor
placement in environmental monitoring”, Int. Journal
Appl. Math. Computer Science, 2010, vol. 20, no. 3,
pp. 445 – 458.
Qing Hua Xia, Ser Yong Lim, M. H Ang Jr, Tao Ming
Lim, 2004, Adaptive Joint Friction Compensation
Using a Model-Based Operational Space Velocity
Observer, 2004 IEEE Int Conf on Robotics and Aut.,
New Orleans, 16 May, pp 3081-3086.
Krstic, M., Smyshlyaev, A., 2006, Boundary Control of
PDEs: A Short Course on Backstepping Design,
VCSB, 2006.
Camarillo, D., Milne, C., 2008, Mechanics Modeling of
Tendon – Driven Continuum Manipulators, IEEE
Trans. On Robotics, vol. 24, no. 6, December 2008,
pp. 1262 – 1273.
Bonchis,A, P. I. Corke, D. C. Rye, Q. P. Ha,2001,
Variable structure methods in hydraulic servo systems
control, Automatica 37 (2001) 589}595
Orlov,Y., A. Pissano, E. Usai, 2011,Exponential
Stabilization of the Uncertain Wave Equation via
Distributed Dynamic Input Extension, IEEE Trans.
Aut Control, vol 56, No1, pp212-218.
Krstic, M., A. Smyshlyaev, 2006,“Boundary Control of
PDEs: A short course on backstepping design”,
VCSB, 2006.
Popescu, N., Popescu, D., Ivanescu, M., 2013, A Spatial
Weight Error Control for a Class of Hyper-Redundant
Robots, IEEE Trans on Robotics, vol 29, No 4 ,August
2013 (in press)
APPENDIX
For the desired state
,) the W-Error
dynamics can be obtained from (1), (7), (3), (9), as
(in order to simplify the notation, the index
is
omitted),
̃
̃
Λ
̃
∆
0
,0
,0
(A1)
̃(0)0 where
are determined by (15),
is
obtained from the relation
and the constraint (5) becomes,
̃̃
Let us consider the Liapunov function
1
2
̃
1
2
Λ
̃
̃̃
where is a positive constant that satisfies the
condition
4
Λ
This inequality ensures that V is a positive definite
function (Silvester’s Theorem (Krstic,2006)).The
time derivative will be
̃
̃
Λ
̃
̃
̃
̃
̃
(A2)
By evaluating (A2) along with the solutions of
(A1),with the control law (17), we obtain
̃
Λ
̃
̃
̃
̃
̃
̃
̃
(A3)
or
̃
Λ
̃
̃
̃
̃
+
̃
̃
̃
̃
(A4)
From (A4), we infer that
̃
̃̃
|
̃
|
|
̃
|
̃
̃
̃
|
̃
|
̃
|
̃
|
̃
Using these inequalities, (A4) can be rewritten as
̃
̃
1
2
1
2
Λ
̃
̃
or
̃
̃
̃
̃
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
56

The stability condition requires as the matrix Q to be
positive definite,
Λ
1
4
0
that corresponds to the condition (18) of Theorem 1.
AHybridControlSystemforaTentacleArm
57
