From Object-oriented Programming to Service-oriented Computing

How to Improve Interoperability by Preserving Subtyping

∗

Diana Allam, Herv

e Grall and Jean-Claude Royer

ASCOLA Group, EMN-INRIA, LINA,

epartement Informatique,

Ecole des Mines de Nantes, Nantes, France

Keywords:

Service-oriented Architecture, Object-oriented Programming, Interoperability, Loose Coupling, Subtyping.

Abstract:

The object-oriented paradigm is increasingly used in the implementation and the use of web services. How-

ever, the mismatch between objects and document structures in the wire has a negative impact over interoper-

ability, more particularly when subtyping is involved. In this paper, we discuss how to improve interoperability

in this context by preserving the subsumption property associated to subtyping. First we show the weaknesses

of existing web service frameworks used for serialization and deserialization. Second we propose new foun-

dations for serialization and deserialization, which leads to the speciﬁcation of a new data binding between

objects and document structures, compatible with subtyping.

1 INTRODUCTION

Web services are message-oriented systems based on

document exchanges. But the development of web

services on both client and server sides is increas-

ingly based on object-oriented implementations. This

raises the problem of impedance mismatch between

objects and tree structures in XML or JSON (L

ammel

and Meijer, 2007): it is difﬁcult to preserve object

properties after serialization and deserialization. This

is due to the differences in the data models and the

type systems between the object-oriented paradigm

and the structural one. Such problems are currently

hidden because of restrictions imposed by the cur-

rent practice for the implementation of web services.

According to the current practice, interoperability is

achieved by twining the required interface at the client

with the provided one at the server. In that way, web

services involve a tightly coupled architecture rather

than a loosely coupled one, which contradicts the

standard approach for Service Oriented Architecture

(SOA).

Among the restrictions imposed in the current

practice for web services, we ﬁnd subtyping, which is

useful for web service interoperability as noticed for

instance by (Carpineti and Laneve, 2006), (Lee and

Cheung, 2010) and (Kourtesis and Paraskakis, 2009).

Currently, object-oriented frameworks fail to preserve

∗

This work has been supported by the CESSA ANR

project (see http://cessa.gforge.inria.fr).

subtyping in its object deﬁnition. However it is possi-

ble to remove this gap while considering current tech-

niques for serialization and deserialization: an extra

adaptation on the client side is then required to make

the subtype and the supertype compatible. Thus, this

solution is not consistent either with the principle of

loose coupling: the client and the server cannot be

considered as black boxes.

In order to preserve subtyping while being con-

form to the loose coupling principle, we propose

new foundations for serialization and deserialization,

based on commutative diagrams as found in category

theory (Pierce, 1991). The implementation will give

rise to a new data binding framework for the two most

common technologies for web services, RESTful and

SOAP.

This paper is structured as follows: in Sec. 2, we

present a general view of interoperability between a

client and a server in existing object-oriented frame-

works for RESTful and SOAP Web services. In

Sec. 3, we present two problems related to subtyping

in the case of a dynamic switching between services.

In Sec. 4, we formalize the serialization and deserial-

ization processes and provide their speciﬁcation with

commutative diagrams. In Sec. 5 we conclude this pa-

per by proposing a solution to the subtyping problems

in the formal framework proposed and by stating the

position we will defend in future work.

169

Allam D., Grall H. and Royer J..

From Object-oriented Programming to Service-oriented Computing - How to Improve Interoperability by Preserving Subtyping.

DOI: 10.5220/0004405401690173

In Proceedings of the 9th International Conference on Web Information Systems and Technologies (WEBIST-2013), pages 169-173

ISBN: 978-989-8565-54-9

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

2 INTEROPERABILITY IN

OBJECT-ORIENTED

FRAMEWORKS FOR WEB

SERVICES

In this section we show how the web service inter-

operability between a client and a server is ensured

in object-oriented frameworks and how it can be im-

proved with subtyping.

A View on Document Exchanges. Based on our

observations on some frameworks and standards, like

JAX-WS, JAX-RS and Restlet, we deduce a general

common exchange process of messages for existing

object-oriented frameworks for web services. At each

side, either the client side or the server one, mes-

sages at emission and reception must cross four levels

of message types. These four levels link the object-

oriented environment to the serial environment in the

wire. Starting from the object-oriented level, we dis-

tinguish four levels:

1. Data level which refers to the input and output

types of the service operations declared at the

client (in the proxy interface) or at the server (in

the service interface)

2. Marshallable level which refers to the reiﬁcation

format of Data. The marshallable message for-

mat is the essential message transformation which

makes the difference between the two web ser-

vice models: SOAP and RESTful. As SOAP is

an activity-oriented model, the marshallable mes-

sage corresponds to an activity. Thus, two types

are associated to each declared service operation.

The ﬁrst type is associated to the request on the

operation, often named with the operation name,

and has as attributes the input parameters of the

operation. The other type is associated to the re-

ply which contains an attribute having the return

type of the operation. For the RESTful model,

which is resource oriented, transmitted messages

must be resources. Here, marshallable types are

equal to Data types.

3. Serializable level which refers to the type of mes-

sages ready to be serialized. These types corre-

sponds to tree types associated to the marshallable

types. In web service development practices, they

are generated from the serialization annotations

added into the marshallable types.

4. Serial level which refers to the message format

ready to be sent in the wire. Serial messages are

often represented in XML or JSON format.

Message transformations across these four levels at

the client side is illustrated in Figure 1. These four

levels appear in a symmetric way at the server side.

This ﬁgure shows the different conversions applied

on a message due to a function call f (b), where f

has type A → R and b has type B, a subtype of A. The

ﬁgure distinguishes the SOAP and RESTful cases at

the marshallable level as we mentioned before. For

RESTful, the marshallable message is the data b at

emission and a data r, an instance of R, at reception.

At emission in SOAP, the marshallable message is b

instance of f

where f

is a reiﬁcation format for

function calls f (b). At reception in SOAP, the mar-

shallable message is r

, an instance of f

out

where f

out

is a reiﬁcation format for function results r.

Twining Development Interfaces. Building a se-

rial message from a data at emission then building a

data from the serial message at reception must lead

to an equivalent instance. Therefore, an interoper-

ability is required between the exchange levels at the

client side and at the server side, as it is deﬁned in Fig-

ure 1. According to the current practices of web ser-

vice implementations, this interoperability is achieved

by tightly coupling the client and the server. The

object-oriented environment is associated to a struc-

tural interface expressed with Web Service Descrip-

tion Language (WSDL) or Web Application Descrip-

tion Language (WADL). Clients calling a web service

must get this structural service interface and gener-

ate locally the corresponding types. Therefore, the

declared operations at the client and the server are

equal. Consequently, for the request and the response,

the four levels for messages at the client side and the

server side respectively exactly match, deﬁning each

time a serialization process and an inverse deserial-

ization process.

Interoperability and Subtyping. From a type-

theoretical point of view, the equality between de-

clared operations at the client and the server is not

required to ensure a correct interoperability. The pro-

vided operation by a web service could be a subtype

of the required one by the client, as recalled for in-

stance by (Seco and Caires, 2000). Hence, according

to the variance properties for subtyping, the argument

type of the required operation must be a subtype of

the argument type of the corresponding provided op-

eration; and the return type of the required operation

must be a supertype of the return type of the provided

operation.

In the following section, we aim at showing weak-

nesses in existing frameworks for serialization and de-

serialization: they fail to preserve the subsumption

WEBIST2013-9thInternationalConferenceonWebInformationSystemsandTechnologies

170

Figure 1: Message transformations from object instances to serial messages and inversely at the client side.

property associated to subtyping when they respect

the loose coupling principle.

3 SUBTYPING PROBLEMS

In order to test the preservation of subtyping while re-

specting the loose coupling principle, we propose a

scenario where a client can switch between two web

services related by subtyping. We assume that the

client is initially conﬁgured according to a Web Ser-

vice 1 interface. Then, this client would switch to a

Web Service 2, a compatible substitution of Web Ser-

vice 1. Switching between services having similar

roles is more and more used in dynamic environments

as in (Srirama et al., 2006) and (Zaplata et al., 2009).

The ideal case would be by doing such a switch au-

tomatically without involving any modiﬁcation to the

system because a web service is replaced by a com-

patible one. That way, we ensure a perfect loose cou-

pling because no modiﬁcations are required to ensure

a correct interoperability. However, this ideal solution

is out of the scope of existing frameworks for serial-

ization and deserialization. In the following we will

show the interoperability weaknesses in this context

by considering two subtyping examples. The ﬁrst ex-

ample considers subtyping on provided and required

operations. The second one considers subtyping be-

tween Data types used as input arguments.

The tests are done using Apache CXF framework

and JAXB Data Binding (the default one in CXF),

which are popular standards and can be considered

as paradigmatic. These tests consist to verify if an

emitted instance could be rebuilt at reception as an

instance of a supertype. The preservation of the dy-

namic binding (proper to object-oriented languages)

from the client side to the server side is out of our in-

terest for these tests. In order to study interoperability

in the two web service models, SOAP and RESTful,

we consider examples that can be deployed with both

models.

http://cxf.apache.org/

Figure 2: Interoperability and subtyping between re-

quired/provided operations.

Subtyping between Provided and Required Oper-

ations. Figure 2 illustrates a view of the ﬁrst exam-

ple in SOAP and RESTful. Here, the operation pro-

vided by Web Service 2 can replace the one provided

by Web Service 1 because the input type B is a subtype

of the input type A, according to the object-oriented

deﬁnition. The client always sends B instances when

calling the op service. An overview of the tests done

between Client and Web Service 2 is given in Table 1.

In this table, we note B ≡ A if B has exactly the same

attributes as A else it is noted B 6≡ A.

Table 1 shows that interoperability works per-

fectly for RESTful while it works partially for SOAP.

Subtyping between Data Types. Figure 3 illus-

trates a view of the second example in SOAP and

RESTful. Here, Web Service 2 can replace Web Ser-

vice 1 because it declares exactly the same service.

There is only one difference: Web Service 2 does not

know subtype B, which is an implementation detail.

We consider that the client sends B instances when

calling the op service operation. Table 2 shows an

overview of the tests done between Client and Web

Service 2. In this table, a type is called external when

its instances can be exposed to the external world.

Thus, they can be serialized according to speciﬁc se-

rialization annotations for this type. Otherwise, the

type is called internal. In that case, if an instance of

FromObject-orientedProgrammingtoService-orientedComputing-HowtoImproveInteroperabilitybyPreserving

Subtyping

171

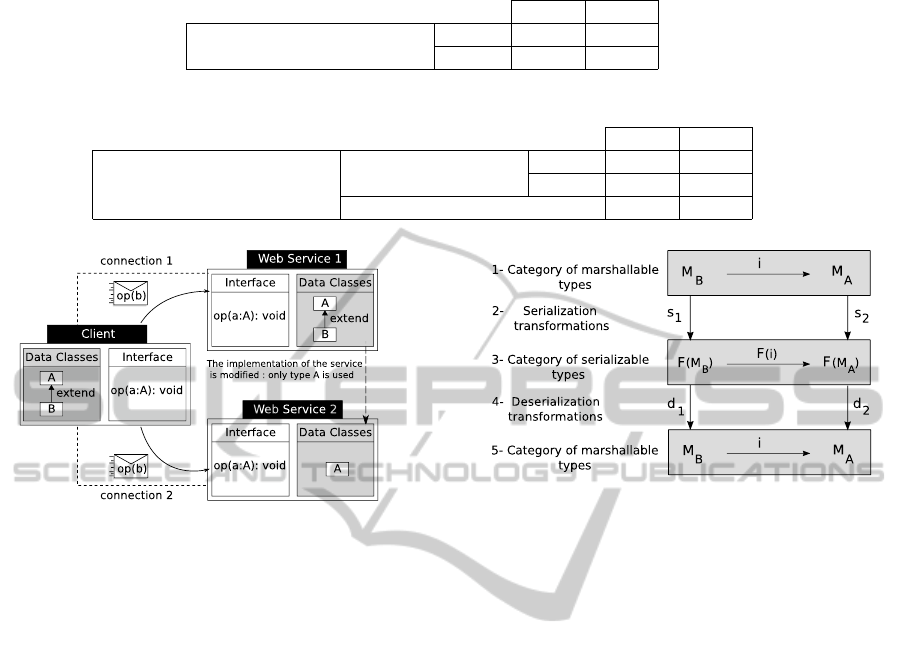
Table 1: Results of tests on cxf framework for the example of Figure 2.

SOAP REST

Interoperability is preserved B ≡ A Yes Yes

B 6≡ A No Yes

Table 2: Results of test on cxf framework for the example of Figure 3.

SOAP REST

B is an external type B ≡ A Yes No

Interoperability is preserved B 6≡ A No No

B is an internal type Yes No

Figure 3: Interoperability and subtyping over Data Types.

such a type is sent to the external world, we consider

the serialization annotation of its external supertype.

Table 2 shows that interoperability fails for REST-

ful while it works partially for SOAP.

4 INTEROPERABILITY

FORMALIZATION

In order to ﬁx the subtyping issues previously pre-

sented, in this section we aim at giving a formalization

of the problem by referring to commutative diagrams.

The message exchange mechanism of Figure 1 can

be summarized as follows: in object-oriented frame-

works for web services, an emitted message is an in-

stance of a marshallable type. It will be transformed

to a serializable message which is then serialized into

a serial message to be transmitted in the wire. At re-

ception, the serial message is deserialized into a se-

rializable message which is transformed into an in-

stance of the expected marshallable type. This mech-

anism can be formalized in a diagram by deﬁning two

categories, a functor and some transformations in or-

der to go from one category to another:

1. Category of Marshallable Types: this category

contains marshallable types as points and typed

functions as arrows,

Figure 4: Fundamental Diagram for Serialization and Dese-

rialization.

2. Category of Serializable Types: this category

contains serializable types as points and typed

functions as arrows,

3. Binding Functor: a mapping from marshallable

types to serializable types, extended to arrows,

4. Transformations: converting a message from a

marshallable type to a serializable type is achieved

by a serialization transformation. Inversely, con-

verting a message from a serializable type to a

marshallable type is achieved by a deserialization

transformation.

In such a formalization, we consider that it is use-

less to specify a category for serial types because se-

rializable messages essentially are trees, which are

fully serializable: by using a depth-ﬁrst traversal and

a parenthesis notation, we can convert a tree into a se-

rial data and by using the inverse function, come back

to the original tree.

In Figure 4, we illustrate our formalization by con-

sidering that an instance of type B must be sent to a

destination waiting an instance of supertype A. Two

marshallable types, M

and M

, are associated re-

spectively to A and B according to the deﬁnition given

in Figure 1. These two marshallable types are re-

lated by an embedding i which allows to convert an

instance of type M

into an instance of type M

, due

to the subtyping relation between A and B. The bind-

ing functor F allows two serializable types, F(M

)

WEBIST2013-9thInternationalConferenceonWebInformationSystemsandTechnologies

172

and F(M

), to be associated to M

and M

respec-

tively. These two serializable types are related by the

corresponding embedding F(i) that allows to convert

any instance in F(M

) into F(M

). In order to con-

vert messages between categories, two serialization

transformations, s

and s

, transform the instances

of M

and M

to their respective serializable forms

in F(M

) and F(M

). Likewise, two deserialization

transformations, d

and d

, transform the instances

of F(M

) and F(M

) to their respective marshallable

forms in M

and M

In a diagram like this, what properties can we as-

sume? First, it is natural to specify that the composi-

tion of the serialization transformation with the dese-

rialization transformation produces the identity trans-

formation, modulo a natural equivalence over mar-

shallable types asserting that two objects are equiv-

alent if their serialization is equal. Second, the dia-

gram in Figure 4 may be commutative: all paths with

the same source and target deﬁne by composition the

same function, modulo the natural equivalence over

marshallable types.

Actually, these two assumptions are fundamental

to solve the subtyping issues previously described as

we will discuss in the next section.

5 DISCUSSION AND FUTURE

WORK

In both examples described in Figures 2 and 3, the

whole process is described by ﬁnding a path join-

ing M

to M

by crossing the category of serializ-

able types. Actually, the path that causes problems is:

→ F(M

) → F(M

) → M

. The trouble comes

from an erroneous conversion function from F(M

)

to F(M

), namely F(i) : F(M

) → F(M

). It is con-

sidered as equal to the identity function, which is a

violation of the commutativity property. With this

value, the composition of the different functions over

the path is not well-deﬁned in some cases, which gen-

erates the errors observed. But with the commutativ-

ity assumption, the problem can be tackled. Indeed,

the conversion function can be easily computed:

F(i) = d

;i;s

It is obtained by composing the deserialization trans-

formation with the embedding function and ﬁnally the

serialization transformation.

Practically, F(i) corresponds to a projection and

possibly a renaming for the serializable structures.

For instance, assume that type A has one serializ-

able attribute x, while its subtype B has another se-

rializable attribute y. An instance of F(M

) could be

represented by the structure B(x(val

), y(val

)) (using

a parenthesis notation) while an instance of F(M

)

could be represented by the structure A(x(val

)).

Then the conversion function F(i) renames the mes-

sage root element from B to A and projects the couple

of values (x, y) into x. Finally, the conversion function

F(i) can be integrated in the framework for serializa-

tion and deserialization at reception on both client and

server sides, in a fully transparent way, which satisﬁes

the loose coupling principle: this solution does not re-

quire any extra adaptation on the client side when a

switch is done between compatible services.

Finally, it turns out that the diagram, when as-

sumed commutative, could become a well-founded

speciﬁcation for serialization and deserialization. Its

implementation could lead to the deﬁnition of a new

data binding between marshallable types and serializ-

able types, preserving the subsumption property asso-

ciated to subtyping, and therefore improving interop-

erability.

REFERENCES

Carpineti, S. and Laneve, C. (2006). A basic contract lan-

guage for web services. In Programming Languages

and Systems, 15th European Symposium on Program-

ming (ESOP), volume 3924 of LNCS, pages 197–213.

Springer.

Kourtesis, D. and Paraskakis, I. (2009). Semantic Enter-

prise Application Integration for Business Processes:

Service-Oriented Frameworks, chapter IV. Business

Science Reference, Hersley.

ammel, R. and Meijer, E. (2007). Revealing the x/o

impedance mismatch: changing lead into gold. In

Proceedings of the 2006 international conference on

Datatype-generic programming, SSDGP’06, pages

285–367, Berlin, Heidelberg. Springer-Verlag.

Lee, T. Y. L. and Cheung, D. W. (2010). Formal models

and algorithms for XML data interoperability. JCSE,

4(4):313–349.

Pierce, B. C. (1991). Basic Category Theory for Com-

puter Scientists (Foundations of Computing). The

MIT Press, 1 edition.

Seco, J. C. and Caires, L. (2000). A basic model of typed

components. In ECOOP, pages 108–128.

Srirama, S. N., Jarke, M., and Prinz, W. (2006). Mobile web

service provisioning. Advanced International Confer-

ence on Telecommunications / Internet and Web Ap-

plications and Services, International Conference on,

0:120.

Zaplata, S., Dreiling, V., and Lamersdorf, W. (2009). Re-

alizing mobile web services for dynamic applications.

In Godart, C., Gronau, N., Sharma, S., and Canals, G.,

editors, Proceedings of the 9th IFIP Conference on e-

Business, e-Services, and e-Society (I3E 2009), pages

240–254. Springer.

FromObject-orientedProgrammingtoService-orientedComputing-HowtoImproveInteroperabilitybyPreserving

Subtyping

173