
Nonlinear Modeling and Parameter Identification of Dynamic
Friction Model in Tendon Sheath for Flexible Endoscopic Systems
T. N. Do
1
, T. Tjahjowidodo
1
, M. W. S. Lau
2
and S. J. Phee
1
1
School of Mechanical and Aerospace Engineering, Nanyang Technological University,
Robotic Research Centre, 50 Nanyang Avenue, Singapore, 639798, Singapore
2
School of Mechanical and Systems Engineering, Newcastle University International Singapore (NUIS),
180 Ang Mo Kio, Avenue 8, Block P, Room 220, Singapore, 569830, Singapore
Keywords: Surgical Robot, Tendon Sheath, Dynamic Friction, Sliding Regime, Presliding Regime, Hysteresis.
Abstract: Minimally Invasive Surgery (MIS) has established a revolution in surgical communities, with its many
advantages over open surgery. The need of more simplicity and high maneuverability makes the tendon
sheath a very suitable mechanism in flexible endoscopic systems. Due to the restriction on size constraints
and sterilization problems, traditional sensors cannot be mounted on the tool tips of a slave manipulator.
Moreover, in the presence of nonlinear friction and hysteresis between the tendon and the sheath, it is
extremely difficult to control the precise motion and sense the force during the operation. This paper
proposes a new dynamic friction model to estimate the force at the end effector for the tendon sheath
mechanism. The proposed friction model can adapt with any initial pretension of the tendon and any
configuration of the sheath. The nonlinearities in both sliding and presliding regimes can be captured by
using an internal state variable and functions dependent velocity and acceleration. A specific setup has been
designed in order to measure the friction force between the tendon and the sheath. Finally, the validity of the
identified model is confirmed by a good agreement of its prediction and experimental data.
1 INTRODUCTION
The introduction of robotic assistance for minimally
invasive surgery (MIS) opened a revolution in
surgical communities during the past few years, with
the advantages to perform complex surgical tasks
such as intracorporeal suturing. MIS has many
benefits such as a reduction of trauma and healing
time, reduction of lost blood, enhancement of better
cosmetic and faster recovery for the patients
(Nagahiro et al., 2001; Förster et al., 2002; Bodner et
al., 2004). Natural Orifice Transluminal Endoscopic
Surgery (NOTES) is an emerging surgical
technology that accesses the peritoneal cavity
without any abdominal incisions. In a laparoscopic
surgery, surgeons directly use their hand to operate
surgical instrument. However, in laparoscopic
surgery using robots, surgeons perform the surgical
tasks using a master
console to control a slave
manipulator inside the patients as in Figure 1.
To actuate the slave manipulator in flexible
endoscopic systems, tendon sheath mechanism is
preferred. This type of mechanism consists of a
hollow helical coil wire and an internal cable (Phee
et al., 2010). The tendon-sheath system can pass
through a long narrow and tortuous path, meaning
that it can operate in small working areas, and
allows for a drastic reduction of system size.
Moreover, it does not require high electrical power
or actuator at distal end to operate the slave. The
need of flexible actuation such as low bulkiness,
high maneuverability and degrees of freedom, small
in size, light weight, cheaper and simpler design, and
safety on human body, have made the tendon-sheath
a very suitable mode for transmission. Due to the
size constraints and sterilization problems,
traditional sensors cannot be mounted at end
effectors. Moreover, nonlinearities in the tendon
sheath cause major challenges not only in modelling
but also in enhancing system performances. In order
to enable surgeons to feel as they have in direct
touch on the tissue, several activities proposed the
model parameters for tendon sheath in terms of
analyses of lumped mass model combined with
Coulomb friction or Dahl model (Dahl, 1968), in
which a set of algorithms provides an estimation for
5
N. Do T., Tjahjowidodo T., W. S. Lau M. and J. Phee S..
Nonlinear Modeling and Parameter Identification of Dynamic Friction Model in Tendon Sheath for Flexible Endoscopic Systems.
DOI: 10.5220/0004409800050010
In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2013), pages 5-10
ISBN: 978-989-8565-71-6
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)
force at end effectors.
Kaneko and his colleagues (Kaneko et al., 1991)
analytically modelled tendon sheath in terms of
small elements, in which apparent tendon stiffness
was combined with lumped model parameters and
Coulomb friction to estimate the tendon tension
along the sheath. Similar approach was proposed by
researchers at University of Bologna (Palli and
Melchiorri, 2006; Palli et al., 2009; Palli et al.,
2012). They replaced Coulomb friction model by
Karnopp and Dahl friction models to characterize
nonlinear hysteresis in the tendon sheath. However,
their approaches are only based on the assumption of
constant pretension tendon and sheath curvature for
each lumped element. Later, Agrawal and Bin
(Agrawal et al., 2008; Agrawal et al., 2010) used a
set of partial differential equations to predict the
load transmission of the tendon sheath with any
pretension and the sheath curvature. However, it is
too complicated when the sheath shape in terms of
helical or spatial types. Moreover, in the case of
static friction model, like Coulomb, it is extremely
lost the force information when the tendon is in
stationary state.
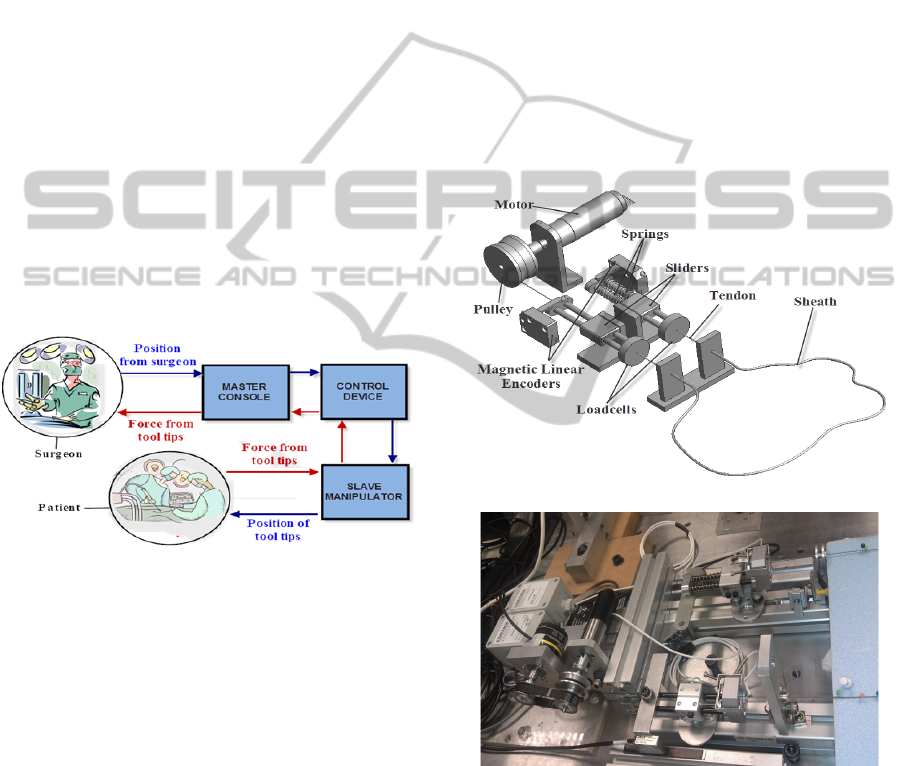
Figure 1: Overview of a surgical system.
Unlike existing approaches in the literature, a
dynamic friction model that we propose in this paper
is based nonlinear hysteresis friction in relations
with acceleration and velocity, and under several
assumptions such as fixed sheath shape, no slack of
the tendon. It considers the tendon sheath as one
element and is able to capture well hysteresis force
for both sliding and presliding regimes. It has been
shown that when the tendon sheath is moving at
small displacement and slow velocity, the proposed
model can predict exactly the force transmission in
the system. This is not available on the current
approaches. The
proposed model is subsequently
validated through experiments and suitable
identification technique. The limitation of the
proposed model in applying the force feedback and
position control will be discussed at the end of this
paper.
2 EXPERIMENTAL WORK
2.1 Experimental Setup
In order to observe the friction phenomena between
the tendon and the sheath, an experiment setup has
been conducted as shown in Figure 2. For a flexible
endoscopic system using tendon sheath mechanism,
the slave manipulator is actuated by a cable passing
through a sheath. The nonlinearities occur in the
motion cause tension losses. If the higher pretension
is applied, the slack can be avoided but causes
higher friction force. In contrast, the lower
pretension leads to slower friction force but causes
tendon slacking. Therefore, in this experiment, we
applied a suitable pretention for the tendon in order
to avoid the tendon slacking.
a) Schematic of the setup.
b) A general view of the real setup.
Figure 2: Experimental setup.
The system is actuated by a Faulhaber
2642W024CR DC servomotor with a gearhead with
ratio of 134:1 via a pulley and a cable. Two load
cells LW-1020-50 from Interface Corporation are
utilized to measure the tendon tension at two ends of
the tendon sheath. In order to maintain the
bidirectional motion between tendon and sheath, two
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
6

linear springs are used at distal ends of the system.
The main purpose of using two springs is to simulate
the force at end effector and to create a suitable
initial pretension for the tendon. To hold the load
cells, two linear sliders are used, which are free to
move in space as well as to serve as platforms for
guiding two linear springs to slide. Two magnetic
linear encoders LM15 with high resolution of 5μm
from RLS d.o.o are also used. One is mounted at the
proximal end to provide the position and velocity
information for the input signal and motor control,
while the other is attached at the end effector to
measure its position and velocity. In the middle, a
tendon and sheath are assembled for transmitting
forces from the proximal end to the end effector.
The tendon from Asahi Intecc Co. with the size of
WR7x7OD0.27mm Teflon coated wire ropes outside
is used. The sheath is round-wire coil, also from
Asahi Intecc Co., with inner diameter of 0.36 mm
and outer diameter of 0.8 mm. Both, the tendon and
the sheath are fixed in the platform, which can free
to regulate the sheath shape. The motor is driven by
using ADVANCED motion controls 25A8PWM
servo drive, while each load cell is connected with a
DCA compatible signal conditioner from Interface.
The whole system is controlled by a simple PID
controller in combination with MATLAB Simulink
tool from MathWorks, Inc. and a dSPACE DS 1104
controller board from dSPACE Inc. During the
measurements, various displacement excitations are
provided by the motor and controllers to the system.
Different frequencies and amplitudes of sinusoidal
excitations are also applied to capture the behaviours
of tendon sheath friction during the experiments.
2.2 Experimental Results
In general, a tendon sheath mechanism can be
viewed as an element with one input: displacement
(or velocity), and one output: displacement (or
velocity). The force balance for the tendon sheath as
one element can be written as:
0
in out
TT F
(1)
where
in
T
is the tension input from master console,
out
T
is the tension output at end effector,
F
is the
friction force occurring when the tendon slides on
the sheath. The tension input
in
T
and output
out
T
can
be measured by two load cells. Then the friction
force
F
can be obtained by Eq. (1). The position
input (x) is measured using the magnetic linear
encoder LM15. The experimental results have been
obtained using two sinusoidal signals at the input
side, i.e. 1hz and 0.8hz, and are shown in Figure 3.
a) Experimental results with an input sinusoidal signal of 1hz.
b) Experimental results with an input sinusoidal signal of 0.8hz.
Figure 3: Experimental results.
3 TENDON SHEATH SYSTEM
AND FRICTION MODELLING
The friction force
F
in Eq. (1) is our main concern.
Responding to the problems of tendon sheath as in
above experimental results, a novel dynamic friction
model for tendon-sheath is proposed here.
Figure 4: Model of tendon sheath with one element.
The model considers the system as a single
degree of freedom (SDOF) system (Figure 4) with
T
in
T
out
One element
Tendon
Sheath
T
in
T
out
Nonlinear
Friction
NonlinearModelingandParameterIdentificationofDynamicFrictionModelinTendonSheathforFlexibleEndoscopic
Systems
7
an advanced asymmetric friction model to capture
the unique hysteresis loss in the tendon-sheath
system based on the Dahl friction model (Dahl,
1968). A single tendon and a sheath are considered
in this case.
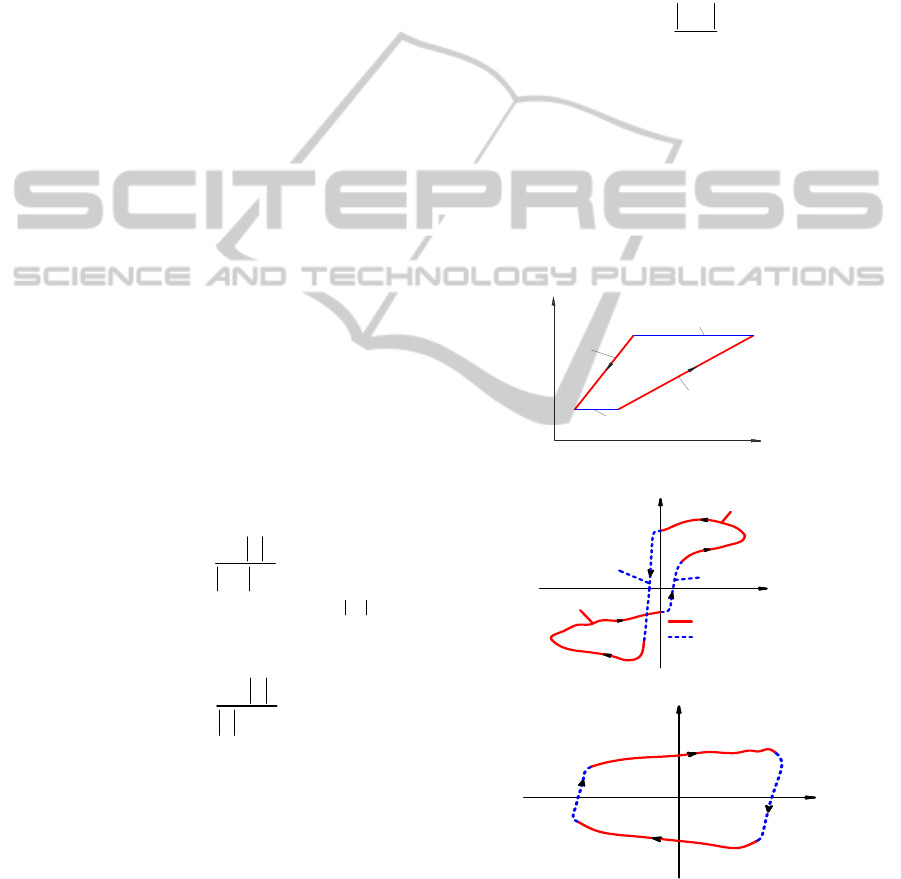
3.1 Asymmetric Hysteresis Friction
Model in Sliding Regime
The main model contains four components
corresponding to acceleration and deceleration.
Current approaches on the friction models are only
based on position and velocity information
(Armstrong-Hélouvry et al., 1994; Canudas de Wit
et al., 1995; Al-Bender et al., 2005). Wojewoda and
his colleagues (Wojewoda et al., 2008) used
acceleration information to capture hysteresis loops
for both acceleration and deceleration parts.
Motivated by this approach, a set of functions
dependent velocity and acceleration will be
formulated in this paper. At steady state, i.e.
() 0t
, the friction force
(,)
f
Fxx
will be
represented by:
( , ) if 0, 0 (2a)
( , ) if 0, 0 (2b)
(, )
( , ) if 0, 0 (2c)
( , ) if 0, 0 (2d)
anvp
anvp
f
anvn
anvn
Gxx x x
Gxx x x
Fxx
Gxx x x
Gxx x x
where
,,
x
xx
denote the position input, velocity
input, and acceleration input, respectively.
1
(,)
11
1
1
2
(,) e
with ( , )
1
fxx
anvp
Gxx
x
fxx
x
3
1
(,)
11 2
(,) e + 1-e
x
fxx
apvp
Gxx
2
(,)
23
4
2
5
(,) e
with ( , )
f
xx
anvn
Gxx
x
fxx
x
2
(,)
23
(,) e
f
xx
apvn
Gxx
The coefficients
12312
,,,,
and
12345
,,,,
are constants that control hysteresis loops in the
sliding regime. The subscript letters
a, n, v, p refer to
acceleration, negative direction, velocity, positive
direction, respectively.
3.2 A New Dynamic Friction Model
for both Sliding and Presliding
Regimes
Dahl (Dahl, 1968) formulated a new friction model
that can capture hysteresis in presliding regime by
introducing an internal state
()t
. In a survey of
friction model (Armstrong-Hélouvry et al., 1994), a
simple form for the Dahl model was made by:
()
() () ()
c
xt
txt t
F
(3)
where
c
F
is a Coulomb friction force,
is bristle
stiffness. At steady state, the normalized friction
force
()
c
tF
. From this special property, we
observed that we can replace the constant force
c
F
by the force in sliding regime
(,)
f
Fxx
given by
Eq. (2a-2d).
a) Tension input
in
T
versus tension output
out
T
.
b) Friction force versus velocity.
c) Friction force versus position.
Figure 5: Nonlinear characteristics of friction between
tendon and sheath.
The friction force in the sliding regime and the
Dahl model are included in a unique new model that
Phase 3(EGI)
Phase 4
(IHA)
Phase 1(ABC)
Phase 2 (CDE)
0
T
in
T
out
0
F
v
Sliding regime
Pre-sliding regime
Phase 2
Phase 1
Phase 3
Phase 4
A
C
D
E
I
H
B
G
0
F
x
A
B
C
E
G
I
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
8
can describe nonlinear hysteresis in tendon sheath.
Theproposed model can be given by:
()
() () ()
(, )
f
xt
txt t
Fxx
(4)
() ()Ft t
(5)
Referring back to Figure 5, along the curve AB,
the friction force is in the pre-sliding regime and its
values are represented by a combination of the
dimensionless value
()t
and the stiffness
. This
curve conresponds to Phase 1. At steady state, i.e.
() 0t
, the friction force at sliding regime
() ( , )
f
Ft F xx
, the curves CD and DE corespond
to the acceleration and deceleration directions. This
curve is in the Phase 2 on the right figure. The same
arguments hold for Phase 3 and Phase 4
corresponding to the curves EGI and IHA. A spectial
property of the proposed model is that the transition
from presliding to sliding regime is guaranteed to be
smooth. Moreover, the proposed model captures
well the force when the system is at zero velocity
(Phase 1 and Phase 3).
4 PARAMETER
IDENTIFICATION
OF THE PROPOSED
FRICTION MODEL
To validate the proposed friction model, the
identification experiment was carried out by
applying a sinusoidal input signal in experimental
setup. Parameters of the proposed model are firstly
identified by applying a genetic algorithm (GA)
(Mitchell, 1996) to generate a initial guess of the
parameters. Subsequently, after having a rough
estimation, the obtained parameters are used as an
initial guess in the Nelder-Mead Simplex Method to
refine the result. The whole processes are carried out
by MATLAB Identification Toolbox from
MathWorks. As a measure of performance, the mean
square error (MSE) was used and defined by:
2
1
1
ˆˆ
MSE( )
N
i
F
FF
N
(6)
where
F
is the output (the force values are
measured from the experiment).
For the identification of the friction force in
tendon sheath, 11 parameters have to be identified.
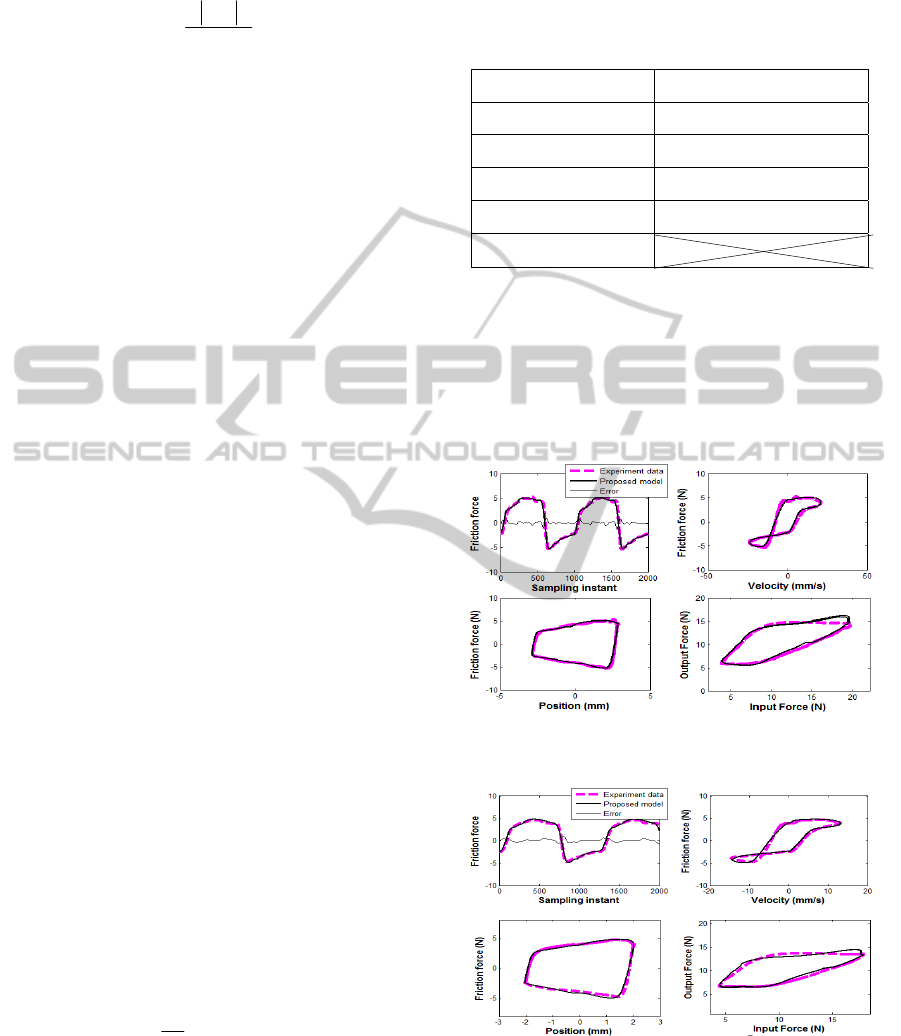
Figure 6 depicts the results of the identification
consisting 11 parameters for a sinusoidal input
signal 1 Hz of both sliding and presliding regimes.
The 11 parameter values are shown in Table 1.
Table 1: Identification result for the proposed model.
1
2.097
2
3.960
1
1.368
3
1.855
1
0.172
4
5.549
2
1.228
5
0.005
2
1.579
17.57
3
0.016
The upper left panel of Figure 6 shows the actual
friction force (dashed line), friction model (solid
line), and the error for both results. The upper right
panel shows the proposed model and actual force
versus velocity, while the lower panel depicts the
friction force of the real data and proposed model in
relation with position.
Figure 6: Identification results compared between the
proposed model and experiment data (for1hz).
Figure 7: Identification results compared between the
proposed model and experiment data (for 0.8hz).
The same results are represented for a sinusoidal
input signal of 0.8 Hz and are shown in Figure 7.
The parameter values in Table 1 are also used in this
case. The proposed model offers the better
NonlinearModelingandParameterIdentificationofDynamicFrictionModelinTendonSheathforFlexibleEndoscopic
Systems
9

estimation results compared to the current approach
utilizing lumped mass model. This means that this
model offers a major advantage of capturing friction
force at area near zero velocity, i.e. when the system
stops, and guarantees a smooth transition from
presling to sliding regimes. Moreover, at small
displacement, the friction force changes very
rapidly. The proposed model can track quite well in
this case as shown in Figure 6 and 7.
5 CONCLUSIONS
This paper has introduced a new dynamic friction
model to solve the haptic feedback problems for
flexible endoscopic system using tendon sheath
mechanism. The proposed model incorporates
acceleration and velocity information in the sliding
regime and uses a modification of the Dahl dynamic
friction model to capture the hysteresis for both
presliding and sliding regimes. The new model can
give a smooth transition between the two regimes
(sliding and presliding regimes) and is capable of
prediction friction near zero velocity.
Validation experiments have been carried out to
evaluate the proposed model. An efficient
identification method (Genetic Algorithm) has firstly
used to generate a rough initial guess of model
parameters. The obtained results have been refined
using the Nelder-Mead Simplex Method. The
comparisons between the proposed model and the
experiment data have shown a good agreement for
the approach. It can be concluded that the proposed
model promises an efficient approach not only in
accurately predicting the force for haptic feedback
but also in any surgical devices that have similar
friction characteristics as the tendon sheath.
Future activities will be conducted by developing
the experimental setup for a pair of tendon sheath
and the proposed model to adapt to any
configuration of the sheath. A hysteresis
compensation for both position and friction force
feedback will be also developed using suitable
nonlinear control schemes and taking into
consideration for higher degrees of freedom in the
system.
REFERENCES
Agrawal, V., Peine , W. J., et al. (2010). "Modeling of
Transmission Characteristics Across a Cable-Conduit
System." Robotics, IEEE Transactions on 26(5): 914-
924.
Agrawal, V., Peine, W. J. , et al. (2008). "Modeling of a
closed loop cable-conduit transmission system".in
Proc. IEEE Int. Conf. Robot. Autom.,Pasadena, CA,
pp. 3407–3412.
Al-Bender, F., Lampaert, V., et al. (2005). "The
generalized Maxwell-slip model: a novel model for
friction Simulation and compensation." Automatic
Control, IEEE Transactions on 50(11): 1883-1887.
Armstrong-Hélouvry, B., Dupont , P., et al. (1994). "A
survey of models, analysis tools and compensation
methods for the control of machines with friction."
Automatica 30(7): 1083-1138.
Bodner, J., Wykypiel , H., et al. (2004). "First experiences
with the da Vinci™ operating robot in thoracic
surgery." European Journal of Cardio-Thoracic
Surgery 25(5): 844-851.
Canudas de Wit, C., Olsson , H., et al. (1995). "A new
model for control of systems with friction." Automatic
Control, IEEE Transactions on 40(3): 419-425.
Dahl, P. R. (1968). "A solid friction model." Aerospace
Corp. El Segundo CA: 31.
Förster, R., Storck , M., et al. (2002). "Thoracoscopy
versus thoracotomy: a prospective comparison of
trauma and quality of life." Langenbeck's Archives of
Surgery 387(1): 32-36.
Kaneko, M., Wada , M., et al. (1991). "A new
consideration on tendon-tension control system of
robot hands. " in Proc. Int. Conf. Robot. Autom., vol.
2, Kyoto, Japan, pp. 1028–1033.
Kaneko, M., Yamashita , T., et al. (1991). "Basic
considerations on transmission characteristics for
tendon drive robots. " in Proc. Int. Conf. Adv. Robot.,
vol. 1, Pisa, Italy, pp. 827–832.
Mitchell, M. (1996). Introduction to Genetic Algorithms,
MIT Press.
Nagahiro, I., Andou , A., et al. (2001). "Pulmonary
function, postoperative pain, and serum cytokine level
after lobectomy: a comparison of VATS and
conventional procedure." The Annals of Thoracic
Surgery 72(2): 362-365.
Palli, G., Borghesan , G., et al. (2009). "Tendon-based
transmission systems for robotic devices: Models and
control algorithms. " in Proc. Int. Conf. Robot. Autom.,
Kobe, Japan, pp. 4063–4068.
Palli, G., Borghesan , G., et al. (2012). "Modeling,
Identification, and Control of Tendon-Based Actuation
Systems." Robotics, IEEE Transactions on 28(2): 277-
290.
Palli, G. and Melchiorri , C. (2006). "Model and control of
tendon-sheath transmission systems. " in Proc. Int.
Conf. Robot. Autom., Orlando, FL, pp. 988–993.
Phee, S. J., Low , S. C., et al. (2010). "Tendon sheath
analysis for estimation of distal end force and
elongation for sensorless distal end." Robotica 28(07):
1073-1082.
Wojewoda, J., Stefanski , A., et al. (2008). "Hysteretic
effects of dry friction: modelling and experimental
studies." Philosophical Transactions of the Royal
Society London, Series A (Mathematical, Physical and
Engineering Sciences) 366(1866): 747-765.
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
10
