Enhanced Iterated Local Search Algorithms for the Permutation Flow

Shop Problem Minimizing Total Flow Time

Xingye Dong

1,2

, Maciek Nowak

, Ping Chen

and Houkuan Huang

School of Computer and Information Technology, Beijing Jiaotong University, Beijing 100044, China

Quinlan School of Business, Loyola University, Chicago, IL 60611, U.S.A.

TEDA College, NanKai University, Tianjin 300457, China

Keywords:

Scheduling, Permutation Flow Shop, Total Flow Time, Iterated Local Search, Neighborhood.

Abstract:

Flow shop scheduling minimizing total ﬂow time is a famous combinatorial optimization problem. Many

algorithms have been proposed to solve it. Among them, iterated local search (ILS) is a simple, efﬁcient and

effective one. However, in existing ILS, one basic insertion neighborhood is generally used, greatly limiting

the search space. In this work, an enhanced iterated local search (EILS) is proposed, using a hybrid of insertion

and swap neighborhoods. The perturbation method also plays an important role in ILS. Two perturbation

methods, the insertion method and a destruction and construction heuristic are tested in this paper. Both

perform signiﬁcantly better in comparison to three state of the art algorithms, indicating that the hybrid use

of insertion and swap neighborhoods is effective for the discussed problem. However, there is no signiﬁcant

difference between the destruction and construction and the insertion perturbation methods.

1 INTRODUCTION

As a simple but efﬁcient and effective metaheuristic,

iterated local search (ILS) has attracted a great deal

of attention (Lourenc¸o et al., 2010). The framework

of ILS is quite simple, with the pseudo code listed in

Figure 1, where s

∗

denotes the best solution found so

far. There are several key components in the ILS al-

gorithm: the method generating the initial solution in

step 1, the local search procedure in step 2, the ac-

ceptance criterion in step 3 and the method to perturb

solution s in step 4.

1. Generate an initial solution s; let s

= s, s

∗

= s;

2. Generate s

= LocalSearch(s

); update s

∗

if bet-

ter solution is found in the process;

3. Let s = Accept(s,s

);

4. If the termination criterion is not satisﬁed, then

generate s

= Perturb(s) and go to step 2; oth-

erwise, output s

∗

Figure 1: Pseudo code of an ILS framework.

The ILS algorithm has been applied to a variety of

combinatorial optimization problems, including the

permutation ﬂow shop scheduling problem (PFSP). In

the PFSP, there are n jobs requiring m operations to be

performed on m machines in the same sequence, i.e.,

no pre-emption is allowed. All of the jobs are avail-

able for processing when the problem begins, the ith

operation needs to be processed on the ith machine,

each machine can serve at most one job at any time,

and an operation can be processed only if the previous

operation is completed and the requested machine is

available. In literature, the solution of the PFSP is

usually presented as a permutation of the jobs.

In practice, local search has been most frequently

implemented as part of a more complex metaheuris-

tic. The metaheuristics for solving the PFSP min-

imizing total ﬂow time include the M-MMAS and

PACO (Rajendran and Ziegler, 2004), the ACO1 and

ACO2 (Rajendran and Ziegler, 2005), the differen-

tial evolution algorithm and iterated greedy algorithm

(Pan et al., 2008), genetic algorithms (Tseng and Lin,

2009; Tseng and Lin, 2010; Zhang et al., 2009) and

the artiﬁcial bee colony algorithm (Tasgetiren et al.,

2011). Local search algorithms are also used in-

dependently and iteratively. For example, Dong et

al. (Dong et al., 2009) propose an ILS algorithm to

solve the PFSP minimizing total ﬂow time, show-

ing improvement over three constructive heuristics

and four metaheuristics. More recently, Dong et al.

Dong X., Nowak M., Chen P. and Huang H..

Enhanced Iterated Local Search Algorithms for the Permutation Flow Shop Problem Minimizing Total Flow Time.

DOI: 10.5220/0004410100580065

In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2013), pages 58-65

ISBN: 978-989-8565-70-9

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

(Dong et al., 2013) presented the multi-restart ILS

(MRSILS), improving the ILS by restarting the local

search from a group of elite solutions. Their experi-

ments show that the MRSILS is better than or com-

parable to ﬁve state of the art metaheuristics, as well

as the ILS presented in (Dong et al., 2009). Finally,

four independent local search methods are developed

by Pan and Ruiz (Pan and Ruiz, 2012) and shown to

be quite effective.

However, a defect in many current state of the art

algorithms is a relatively limited search space. Quite

often, only one neighborhood structure is used for lo-

cal search, e.g., only an insertion neighborhood struc-

ture is used in the ILS algorithms by Dong et al.

(Dong et al., 2009; Dong et al., 2013) and the algo-

rithms by Pan and Ruiz (Pan and Ruiz, 2012). Us-

ing more than one neighborhood structure, as with

variable neighborhood search (VNS), is an effective

way to expand the search space. However, too many

neighborhood structures can lead to a signiﬁcant in-

crease in computation time. Finding an appropriate

balance between search space and computation time

is vital.

In this work, an enhanced ILS (EILS) frame-

work is proposed that uses both insertion and swap

neighborhoods sequentially during the local search.

The use of just one additional neighborhood struc-

ture opens up the search space considerably while

limiting the increase in computational time. In or-

der to further expand the search space, the EILS ap-

plies two perturbation methods, a simple insertion

perturbation method and a destruction and construc-

tion heuristic. The insertion perturbation method is

drawn from Dong et al. (Dong et al., 2013), and the

destruction and construction heuristic is derived from

an iterated greedy algorithm (Ruiz and St

utzle, 2007),

which has been successfully used by Pan and Ruiz

(Pan and Ruiz, 2012).

The proposed EILS is evaluated on Taillard’s set

of benchmark problem instances (Taillard, 1993), and

compared with the MRSILS developed by Dong et al.

(Dong et al., 2013) and the ILS and IGA developed by

Pan and Ruiz (Pan and Ruiz, 2012). These two algo-

rithms have outperformed other algorithms on numer-

ous data instances and they have established the cur-

rent benchmark for comparison. While a great deal

of research now focuses on more intricate and sophis-

ticated metaheuristics, this work shows that a deeper

analysis of the core problem through the utilization of

a simple heuristic such as ILS has considerable poten-

tial to improve established methodologies.

The remainder of this paper is organized as fol-

lows. In Section 2, the formulation of the PFSP with

total ﬂow time criterion is presented. In Section 3,

the EILS is described in detail. The computational re-

sults are illustrated and analyzed in Section 4, and the

paper is concluded in Section 5.

2 PROBLEM FORMULATION

In this paper, the PFSP is discussed with the objective

of minimizing total ﬂow time. This problem is an im-

portant and well-known combinatorial optimization

problem, ﬁrst gaining attention through Johnson’s pi-

oneering work (Johnson, 1954). Many researchers

focus their attention on this problem as it is consid-

ered more relevant to today’s dynamic production en-

vironment (Liu and Reeves, 2001), as it tends to sta-

bilize the use of resources and minimize the work-in-

process inventory (Tseng and Lin, 2009).

In the PFSP, a set of jobs J = {1, 2, . ..,n} avail-

able at time zero must be processed on m machines,

where n ≥ 1 and m ≥ 1. Each job has m operations,

each of which has an uninterrupted processing time.

The processing time of the ith operation of job j is

denoted by p

i j

, where p

i j

≥ 0. The ith operation of a

job is processed on the ith machine. An operation of a

job is processed only if the previous operation of the

job is completed and the requested machine is avail-

able. Each machine processes these jobs in the same

order and at most one operation of each job can be

processed at a time. This problem is usually denoted

by F

|prmu|

∑

(Pinedo, 2001), where F

describes

the environment, prmu is the set of constraints and C

denotes the completion time of job j. Let π denote a

permutation on the set J, representing a job process-

ing order. Let π(k), k = 1, . ..,n, denote the kth job

in π, then the completion time of job π(k) on each

machine i can be computed through a set of recursive

equations:

i,π(1)

∑

r=1

r,π(1)

i = 1,...,m

(1)

1,π(k)

∑

r=1

1,π(r)

k = 1,...,n

(2)

i,π(k)

= max{C

i−1,π(k)

i,π(k−1)

} + p

i,π(k)

i = 2,. . . ,m; k = 2,. ..,n

(3)

Then C

π(k)

= C

m,π(k)

, k = 1,..., n. The total ﬂow

time is

∑

π(k)

, or the sum of completion times on ma-

chine m for all jobs. The objective of the PFSP when

minimizing total ﬂow time is to minimize

∑

π(k)

, or

for short. This problem is NP-complete even with

only two machines (Garey et al., 1976).

EnhancedIteratedLocalSearchAlgorithmsforthePermutationFlowShopProblemMinimizingTotalFlowTime

3 ENHANCED ITERATED LOCAL

As aforementioned, there are four key components in

an ILS algorithm. In this section, three key compo-

nents, initial method, local search procedure and per-

turbation method, are discussed and the framework of

the EILS is illustrated.

3.1 Initialization Method

In literature, a good heuristic is often used as the ini-

tialization method. The H(x) heuristics by Liu and

Reeves (Liu and Reeves, 2001), which rank jobs ac-

cording to the ascending order of a deﬁned index

function reﬂecting weighted total machine idle time

and artiﬁcial ﬂowtime, are highly effective for the this

purpose. H(x) heuristics are used to generate initial

solutions for several state of the art metaheuristics,

such as the four local-search-based algorithms by Pan

and Ruiz (Pan and Ruiz, 2012). Dong et al. (Dong

et al., 2009) used the H(2) method to generate an ini-

tial solution in negligible time, allowing for the ILS

algorithm to perform very well. H(2) is also used in

the MRSILS algorithm (Dong et al., 2013). In this

work, the H(2) heuristic is used to generate initial so-

lutions.

3.2 Local Search Procedure

An efﬁcient local search procedure is very important

to the success of ILS as it mainly determines the so-

lution space that may be explored. Driving the search

to a promising area is vital to an ILS algorithm, such

as with the MRSILS, which is successful because it

extends the search space by generating new start solu-

tions from a set of elite solutions. However, the search

space can also be extended through the use of a local

search based on a variety of neighborhood structures.

In this work, two commonly used local search

methods are jointly applied, insertion and swap. The

neighborhood of an insertion local search is all solu-

tions that may be found by moving a job and inserting

it elsewhere. This is described in Figure 2, where π

∗

denotes the best solution found so far, f lag = true in-

dicates that π

∗

is improved during the search, idx de-

notes the index of the inserting job in π

seq

, and each

of these is a global variable. In this local search, each

of the n jobs is inserted into each of the other n − 1

positions and the current solution is updated when a

better neighbor is found. The job that is being in-

serted is denoted by π

seq

(idx + 1). When the search

is trapped in a local optimum, such that cnt = n in

line 3, it is stopped and the current solution π is re-

turned. The search sequence is determined by π

seq

which equals the start solution π at the beginning, and

then updated when the π

∗

is improved (line 11). This

search sequence scheme is derived from the idea of

the referenced index search method (Rajendran and

Ziegler, 1997).

Insertion LS(π)

1. {

2. Set π

seq

= π, cnt = 0;

3. while(cnt < n)

4. {

5. Find j, where π( j) = π

seq

(idx + 1);

6. Insert π( j) to other n − 1 positions,

respectively, and let π

be the best

generated solution;

7. if(C

< C

)

8. {

9. cnt = 1, π = π

;

10. if(C

< C

∗

)

11. π

∗

= π, f lag = true, π

seq

= π;

12. }

13. else

14. cnt + +;

15. idx = (idx + 1) mod n;

16. }

17. return π;

18. }

Figure 2: Pseudo code of the insertion local search.

The neighborhood of a swap local search is those

solutions that may be found by swapping the posi-

tion of two jobs in the sequence. This is illustrated in

Figure 3, where the π

∗

, f lag and idx have the same

meaning as in the insertion local search. The job be-

ing swapped is denoted by π

seq

(idx + 1). This neigh-

borhood search swaps each job with earlier jobs in the

current solution, and the current solution is updated

when a better neighbor is found. When the search

is trapped in a local optimum, such that cnt = n in

line 4, it is stopped and the current solution π is re-

turned. The search sequence is also determined by

seq

, which equals the start solution π throughout the

procedure. In this search, idx always starts from zero.

There are (n−1)

neighbors in an insertion neigh-

borhood, while n × (n − 1)/2 neighbors in a swap

neighborhood, given that swapping job a with b is

the same as swapping b with a. Since the computa-

tional complexity to evaluate one solution is O(nm),

the computational complexity for evaluating all the

neighbors with both local search methods is at least

O(n

m).

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

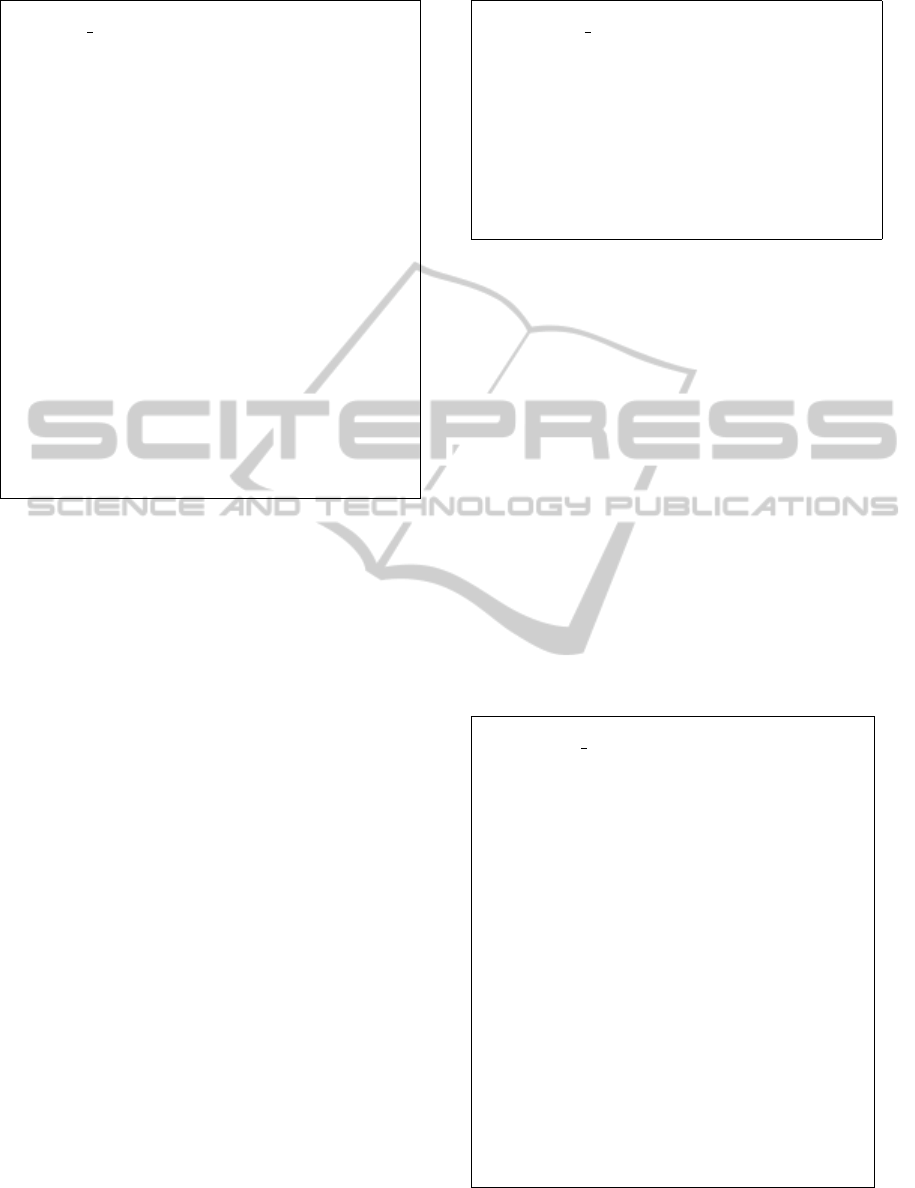
Swap LS(π)

1. {

2. Set π

seq

= π, cnt = 0;

3. Set global variable idx = 0;

4. while(cnt < n)

5. {

6. Find j, where π( j) = π

seq

(idx + 1);

7. Swap π( j) with the jobs earlier

in the sequence, and let π

the best generated solution;

8. if(C

< C

)

9. cnt = 1, π = π

;

10. else

11. cnt + +;

12. idx = (idx + 1) mod n;

13. }

14. if(C

< C

∗

)

15. π

∗

= π, f lag = true;

16. return π;

17. }

Figure 3: Pseudo code of the swap local search.

3.3 Perturbation Method

When the local search procedure is trapped in a local

optimum, a new start solution is generated in order to

continue the local search. The new start solution is of-

ten generated by perturbing an elite solution, such that

the perturbation method plays an important role in the

success of an ILS algorithm. Insertion and swap per-

turbation are two commonly used methods. In litera-

ture, several researchers have reported that the former

performs better than the latter (Tasgetiren et al., 2011;

Dong et al., 2013) and this paper focuses on insertion

perturbation. The insertion perturbation is described

in Figure 4, where idx is a global variable, denoting

the start index of the job to be inserted in the next it-

eration of local search. After perturbation, idx is set

according to the insertion position.

The variable idx is used to avoid cycling, particu-

larly when the new start solution is generated through

insertion perturbation. For example, suppose an elite

solution π

∗

= (1, 2, 3,4,5) is selected for perturbation

to create a new start solution π = (4,1,2,3,5). If job 4

is the ﬁrst repositioned job, then it will be reinserted

to position 4 as π

∗

is a local optimum. In order to

avoid cycling, the job that was moved to generate the

new start solution should be the last one selected in

the following local search.

Another perturbation method comes from the iter-

ated greedy (IG) algorithm, which is introduced by

Ruiz and St

utzle (Ruiz and St

utzle, 2007) to solve

Insertion Perturb(π)

1. {

2. Randomly select a job in π and remove

it from the sequence; Insert the job into

any randomly chosen position (except

in its original position j) ;

3. Set idx = j mod n, π

seq

= π;

4. return π;

5. }

Figure 4: Pseudo code of the insertion perturbation method.

the PFSP minimizing makespan. The IG algorithm

runs iteratively over a destruction and construction

procedure. In the destruction stage, several jobs are

removed randomly from a solution to form a partial

solution, after which the jobs are reinserted sequen-

tially in a greedy way to reconstruct a full solution.

This method has been used by Pan and Ruiz (Pan and

Ruiz, 2012) as a perturbation method in their IGA. In

this work, the destruction and construction procedure

is also used as a perturbation method. It is illustrated

in Figure 5, where d is the number of removed jobs,

reﬂecting the perturbation strength, while π

is a pool

for the removed jobs, and the ﬁrst job in this pool is

denoted by π

(1). In the work of Pan and Ruiz (Pan

and Ruiz, 2012), d is set to 8, which is the value used

here. After perturbation, the global variable idx is set

to zero.

Destruct Construct(π, d)

1. {

2. Define π

, i = 0;

3. while(i < d)

4. {

5. Delete a job from π randomly, and

add the job to the end of π

;

6. Set i = i +1;

7. }

8. while(i > 0)

9. {

10. Insert π

(1) back to π to the posi-

tion where the new partial solution

π is optimized;

11. Delete π

(1) from π

, set i = i −1;

12. }

13. Set idx = 0;

14. return π;

15. }

Figure 5: Pseudo code of the destruction and construction

perturbation method.

EnhancedIteratedLocalSearchAlgorithmsforthePermutationFlowShopProblemMinimizingTotalFlowTime

3.4 Framework of the proposed

Enhanced ILS

The framework of the full EILS is illustrated in Fig-

ure 6, where π

∗

denotes the best solution during the

search, pool indicates a set of elite solutions which is

empty at the start.

1. Deﬁne global variable π

∗

, f lag and idx;

2. Generate an initial solution π; Set pool =

pool size; Let π

∗

= π, idx = 0;

3. while(termination criterion is not satisﬁed)

4. {

5. f lag = f alse;

6. π = Insertion LS(π);

7. π = Swap LS(π);

8. if( f lag)

9. Set pool =

10. if(π /∈ pool)

11. Add π to pool;

12. if(|pool| > pool size)

13. Delete the worst solution in pool;

14. if(|pool| < pool size)

15. π = π

∗

;

16. else

17. Randomly choose one solution from

18. pool as π;

19. Perturb π to generate a new π;

20.}

21.Output π

∗

and stop.

Figure 6: Pseudo code of the proposed EILS.

In literature, there are usually two termination cri-

teria: a maximum number of iterations and limited

computational time. In this work, the latter is applied

on line 3 in order to more easily compare the EILS

with other algorithms. The insertion local search and

swap local search are used sequentially in line 6 and

line 7. If the best solution π

∗

is improved during the

local search, the elite solution set pool is emptied;

otherwise, the local optimum π is added to pool as

an elite solution if it is not in pool yet, and the worst

solution in pool is erased if the size of pool is larger

than its limitation pool size. In this work, the param-

eter pool size is set to 5 as the value is found most

effective in Dong et al. (Dong et al., 2013), though it

is quite robust. This pooling strategy is drawn from

Dong et al. (Dong et al., 2013).

If pool is not full, the best solution found so far,

∗

, is chosen to generate a new start solution π by

the speciﬁed perturbation method. While pool is full,

a solution is randomly chosen from pool and per-

turbed by the speciﬁed perturbation method to gen-

erate a new start solution π. A version of EILS is

implemented for both insertion perturbation and de-

struction and construction perturbation, denoted by

EILS-INS and EILS-DC, respectively. If the inser-

tion perturbation is used and the swap local search

(line 7) is removed, EILS is the same as MRSILS

(Dong et al., 2013), except for the adjustment in the

search sequence. In order to inspect the effect of the

adjusted search sequence, this version of EILS is de-

noted by EILS-NoSwap and compared with MRSILS

in the next section.

EILS is similar to a variable neighborhood search

algorithm; however, in a variable neighborhood

search algorithm, the search is restarted from the ﬁrst

neighborhood when the best solution found so far

is improved (Lourenc¸o et al., 2010). Regardless of

whether the best solution found so far is improved

with local search in EILS, the algorithm will continue

into the perturbation stage.

4 COMPUTATIONAL RESULTS

In this section, EILS is compared with three state of

the art metaheuristics, MRSILS by Dong et al. (Dong

et al., 2013) and two of the four algorithms by Pan and

Ruiz (Pan and Ruiz, 2012). These are some of the best

available metaheuristics for this version of the PFSP,

producing the highest quality solutions available.

MRSILS by Dong et al. (Dong et al., 2013) per-

forms better than the ILS algorithm developed by

Dong et al. (Dong et al., 2009), the discrete dif-

ferential evolution algorithm and the iterated greedy

algorithm by Pan et al. (Pan et al., 2008), the hy-

brid genetic algorithm by Zhang et al. (Zhang et al.,

2009), and the discrete artiﬁcial bee colony and dis-

crete differential evolution algorithms by Tasgetiren

et al. (Tasgetiren et al., 2011).

Pan and Ruiz present four local search based algo-

rithms, one based on the idea of iterated local search

(denoted as PR-ILS) and another on iterated greedy

algorithm (denoted as PR-IGA), with each extended

to a population-based algorithm. PR-ILS and PR-IGA

perform better than the population-based versions, as

well as 12 other powerful metaheuristics published

in recent years. In this work, PR-ILS and PR-IGA

are re-implemented with the same parameters as used

by Pan and Ruiz and compared with EILS. The lo-

cal search procedure used in PR-ILS and PR-IGA is

insertion-based, with a computational complexity of

at least O(n

m).

Each algorithm is implemented in C++, running

on a PC with an Intel Core2 Duo processor (2.99

GHz) with 2G main memory. Though the com-

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

Table 1: Comparison in ARPD for MRSILS, PR-ILS, PR-IGA, EILS NoSwap, EILS INS and EILS DC (0.004 × n

× m ms

CPU time).

n|m MRSILS PR-ILS PR-IGA EILS NoSwap EILS INS EILS DC

20|5 0.007 0.007 0.007 0 0 0

20|10 0 0.002 0 0.004 0.006 0

20|20 0 0 0 0 0 0

50|5 0.339 0.411 0.373 0.342 0.298 0.303

50|10 0.495 0.467 0.436 0.337 0.407 0.391

50|20 0.284 0.378 0.375 0.314 0.405 0.241

100|5 0.328 0.410 0.340 0.350 0.218 0.242

100|10 0.464 0.443 0.513 0.473 0.346 0.523

100|20 0.484 0.540 0.560 0.558 0.387 0.515

Avg. 0.267 0.295 0.289 0.264 0.230 0.246

Table 2: Comparison in ARPD for MRSILS, PR-ILS, PR-IGA, EILS NoSwap, EILS INS and EILS DC (0.012 × n

× m ms

CPU time).

n|m MRSILS PR-ILS PR-IGA EILS NoSwap EILS INS EILS DC

20|5 0.007 0 0 0.007 0 0

20|10 0 0 0 0 0.002 0

20|20 0 0 0 0 0 0

50|5 0.203 0.255 0.233 0.211 0.128 0.139

50|10 0.240 0.354 0.383 0.329 0.259 0.212

50|20 0.209 0.238 0.281 0.176 0.251 0.168

100|5 0.179 0.291 0.191 0.131 0.031 0.073

100|10 0.234 0.308 0.330 0.183 0.123 0.203

100|20 0.289 0.161 0.259 0.153 0.239 0.188

Avg. 0.151 0.179 0.186 0.132 0.115 0.109

puter has two processors, only one is used in the

experiments, as no parallel programming technique

has been applied. In order to show the performance

with increased CPU time, the CPU time is limited to

t × n

× m milliseconds, where t equals 0.004, 0.012

and 0.02, respectively.

The benchmark instances used for analysis are

taken from Taillard (Taillard, 1993), with 120 in-

stances evenly distributed among 12 different sizes.

The scale of these problems varies from 20 jobs and

5 machines to 500 jobs and 20 machines. In the lit-

erature, most metaheuristics are tested on the ﬁrst 90

benchmark instances (Pan et al., 2008; Tseng and Lin,

2009; Tseng and Lin, 2010; Zhang et al., 2009; Tas-

getiren et al., 2011; Dong et al., 2009; Dong et al.,

2013), as the largest instances with 200 and 500 jobs

are too time consuming. This study also uses the ﬁrst

90 instances. For each algorithm, ﬁve independent

runs are performed on each benchmark instance and

the best solution among the ﬁve runs is recorded. The

relative percentage deviation (RPD) is calculated as:

RPD = (F − F

best

)/F

best

× 100 (4)

where F is the result found by the algorithm being

evaluated and F

best

is the best result provided by Dong

et al. (Dong et al., 2013), and it is obtained by running

the MRSILS ten independent times with an extended

time period of 0.4 × n × m seconds for each instance

and the best among these ten runs is chosen as the

result.

The average RPD (ARPD) for each combination

of n and m and the ARPD for all 90 instances are pre-

sented in Table 1 - 3. These tables show that on aver-

age EILS-INS and EILS-DC perform the best, with

EILS-NoSwap, MRSILS, PR-ILS and PR-IGA fol-

lowing in that order.

Compared with MRSILS, EILS-NoSwap only dif-

fers in that it has an adjusted search sequence, which

can avoid cycling. From the experimental results,

EILS-NoSwap performs slightly better than MRSILS

on average, showing the effectiveness of the adjust-

ment. However, the difference is not signiﬁcant.

EILS-INS builds on EILS-NoSwap with the addition

of the swap local search. On average, the ARPD is

lower for EILS-INS, indicating that this local search

has considerable beneﬁt. While several researchers

have reported that the swap local search is not better

than the insertion local search (Tasgetiren et al., 2011;

Dong et al., 2013), this experiment shows that it is

more effective when the two are combined to expand

the search space.

EILS-INS performs slightly better than EILS-DC

EnhancedIteratedLocalSearchAlgorithmsforthePermutationFlowShopProblemMinimizingTotalFlowTime

Table 3: Comparison in ARPD for MRSILS, PR-ILS, PR-IGA, EILS NoSwap, EILS INS and EILS DC (0.02 × n

× m ms

CPU time).

n|m MRSILS PR-ILS PR-IGA EILS NoSwap EILS INS EILS DC

20|5 0.007 0 0.007 0 0 0

20|10 0 0 0 0 0 0

20|20 0 0 0 0 0 0

50|5 0.155 0.191 0.228 0.159 0.160 0.074

50|10 0.192 0.209 0.290 0.167 0.226 0.178

50|20 0.130 0.240 0.151 0.137 0.189 0.062

100|5 0.128 0.203 0.156 0.067 -0.075 0.039

100|10 0.200 0.325 0.238 0.137 0.042 0.147

100|20 0.007 0.096 0.258 0.106 0.004 0.122

Avg. 0.091 0.141 0.148 0.086 0.061 0.069

with the shortest and longest computational times,

while EILS-DC is slightly better with a CPU time

of 0.012 × n

× m ms. This indicates that the more

complex destruction and construction perturbation

method is not necessarily better than the simpler in-

sertion perturbation method. The average RPDs for

PR-ILS and PR-IGA conﬁrm this, with PR-IGA per-

forming slightly better than PR-ILS when computa-

tional time is more limited, while it performs slightly

worse when the time is extended. For the most part,

this is in accordance with Pan and Ruiz (Pan and Ruiz,

2012), where the authors show that PR-IGA performs

slightly better than PR-ILS, but not signiﬁcantly.

5 CONCLUSIONS

In this paper, an enhanced iterated local search frame-

work is proposed to solve the permutation ﬂow shop

scheduling problem minimizing total ﬂow time, an

intensively studied combinatorial optimization prob-

lem. In EILS, two commonly used local search meth-

ods, insertion local search and swap local search, are

used. Further, two different perturbation methods are

applied. EILS searches the solution space intensively

near a group of elite solutions. Compared with some

sophisticated metaheuristics, EILS is simple and easy

to implement.

Comparisons on Taillard’s benchmarks show that

both EILS versions, EILS-INS and EILS-DC, are sig-

niﬁcantly better than three state-of-the-art algorithms.

The improved performance is mainly due to the com-

bined use of the two neighborhood searches. In the

literature, several researchers have reported that the

swap local search is not better than the insertion lo-

cal search, and so only the insertion local search is

used. This work shows that the joint use of insertion

and swap local search results in a more powerful lo-

cal search. Applying this combined strategy to other

metaheuristics may be beneﬁcial, while it may also

be helpful with other combinatorial problems. This

work indicates that the local search-based algorithm

deserves deeper study.

ACKNOWLEDGEMENTS

This work is supported by The Fundamental Research

Funds for the Central Universities of China (Project

Ref. 2009JBM018, Beijing Jiaotong University).

REFERENCES

Dong, X., Chen, P., Huang, H., and Nowak, M. (2013).

A multi-restart iterated local search algorithm for the

permutation ﬂow shop problem minimizing total ﬂow

time. Computers and Operations Research, 40:627–

632.

Dong, X., Huang, H., and Chen, P. (2009). An iterated

local search algorithm for the permutation ﬂowshop

problem with total ﬂowtime criterion. Computers and

Operations Research, 36:1664–1669.

Garey, M., Johnson, D., and Sethi, R. (1976). The complex-

ity of ﬂowshop and jobshop scheduling. Mathematics

of Operations Research, 1:117–129.

Johnson, S. (1954). Optimal two and three-stage production

schedule with setup times included. Naval Research

Logistics Quarterly, 1(1):61–68.

Liu, J. and Reeves, C. (2001). Constructive and composite

heuristic solutions to the p//

∑

scheduling problem.

European Journal of Operational Research, 132:439–

452.

Lourenc¸o, H., Martin, O., and St

utzle, T. (2010). Hand-

book of Metaheuristics, volume 146 of International

Series in Operations Research & Management Sci-

ence, chapter Iterated Local Search: Framework and

Applications, pages 363–397. Springer US.

Pan, Q.-K. and Ruiz, R. (2012). Local search methods for

the ﬂowshop scheduling problem with ﬂowtime mini-

mization. European Journal of Operational Research,

222:31–43.

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

Pan, Q.-K., Tasgetiren, M., and Liang, Y.-C. (2008). A dis-

crete differential evolution algorithm for the permu-

tation ﬂowshop scheduling problem. Computers and

Industrial Engineering, 55:795–816.

Pinedo, M. (2001). Scheduling: theory, algorithms, and

systems. Prentice Hall, 2nd edition.

Rajendran, C. and Ziegler, H. (1997). An efﬁcient heuris-

tic for scheduling in a ﬂowshop to minimize total

weighted ﬂowtime of jobs. European Journal of Op-

erational Research, 103:129–138.

Rajendran, C. and Ziegler, H. (2004). Ant-colony algo-

rithms for permutation ﬂowshop scheduling to mini-

mize makespan/total ﬂowtime of jobs. European Jour-

nal of Operational Research, 155:426–438.

Rajendran, C. and Ziegler, H. (2005). Two ant-colony algo-

rithms for minimizing total ﬂowtime in permutation

ﬂowshops. Computers and Industrial Engineering,

48:789–797.

Ruiz, R. and St

utzle, T. (2007). A simple and effective

iterated greedy algorithm for the permutation ﬂow-

shop scheduling problem. European Journal of Op-

erational Research, 177:2033–2049.

Taillard, E. (1993). Benchmarks for basic scheduling prob-

lems. European Journal of Operational Research,

64:278–285.

Tasgetiren, M., Pan, Q.-K., Suganthan, P., and Chen, A.

H.-L. (2011). A discrete artiﬁcial bee colony algo-

rithm for the total ﬂowtime minimization in permu-

tation ﬂow shops. Information Sciences, 181:3459–

3475.

Tseng, L.-Y. and Lin, Y.-T. (2009). A hybrid genetic lo-

cal search algorithm for the permutation ﬂowshop

scheduling problem. European Journal of Opera-

tional Research, 198:84–92.

Tseng, L.-Y. and Lin, Y.-T. (2010). A genetic local search

algorithm for minimizing total ﬂowtime in the per-

mutation ﬂowshop scheduling problem. International

Journal of Production Economics, 127:121–128.

Zhang, Y., Li, X., and Wang, Q. (2009). Hybrid genetic

algorithm for permutation ﬂowshop scheduling prob-

lems with total ﬂowtime minimization. European

Journal of Operational Research, 196(3):869–876.

EnhancedIteratedLocalSearchAlgorithmsforthePermutationFlowShopProblemMinimizingTotalFlowTime