
A Rule Induction with Hierarchical Decision Attributes
Chun-Che Huang
1
, Shian-Hua Lin
2
, Zhi-Xing Chen
1
and You-Ping Wang
1
1
Department of Information Management, National Chi Nan University, #1, University Road, Pu-Li, Taiwan 545, Taiwan
2
Department of Computer Science and Information Engineering, National Chi Nan University,
#1, University Road, Pu-Li, Taiwan 545, Taiwan
Keywords: Concept Hierarchy, Rough Set Theory, Rule Induction, Decision Making.
Abstract: Hierarchical attributes are usually predefined in real-world applications and can be represented by a concept
hierarchy, which is a kind of concise and general form of concept description that organizes relationships of
data. To induct rules from the qualitative and hierarchical nature in data, the rough set approach is one of the
promised solutions in data mining. However, previous rough set approaches induct decision rules that
contain the decision attribute in the same hierarchical level. In addition, comparison of the reducts using the
Strength Index (SI), which is introduced to identify meaningful reducts, is limited to same number of
attributes. In this paper, a hierarchical rough set (HRS) problem is defined and the solution approach is
proposed. The proposed solution approach is expected to increase potential benefits in decision making.
1 INTRODUCTION
Rough Set (RS) theory was developed by Pawlak
(1982) to classify imprecise, uncertain, or
incomplete information, or knowledge expressed by
data acquired from experience (Pawlak, 1982). The
main advantage of rough set theory is that it does not
require any preliminary or additional information
about data: like probability in statistics or basic
probability assignment in Dempster–Shafer theory
and grade of membership or the value of possibility
in fuzzy set theory (Thangavel and Pethalakshmi,
2009). Over the past years, RST has indeed become
a topic of great interest to researchers and has been
applied in many areas.
Previous Rough Set (RS) Theory approaches
cannot produce rules containing preference order,
namely, cannot achieve more meaningful and
general rules (Sun et al., 2005). RS based induction
often generates too many rules without focus and
cannot guarantee that the classification of a decision
table is credible, for example, generation of
classification rules in Hassanien (2004),
information-rich data to reduce the data redundancy
in Jensen and Shen (2004), the analysis of diabetic
databases in Breault (2001), an unsupervised
clustering in Questier et al., (2002), discovery of
statistical significance rules in Yin et al., (2001), and
an algorithm to infer rules in Phuong et
al., (2001).
Tseng (2008) proposed a new RS method, called
alternative rule extraction algorithm (AREA) to
discover preference-based rules according to the
reducts with the maximum of strength index (SI),
which is introduced in order to identify meaningful
reducts. However, comparison of the reducts using
the Strength Index (SI) is limited to the same
number of attributes. SI should be counted in a
reasonable way of average the weights of selected
attributes.
Moreover, Tseng (2008) and most of the
previous studies on rough sets focused on finding
rules that a decision attribute does not have
hierachical concept. However, hierarchical attributes
are usually predefined in real-world applications and
could be represented though a hierarchy tree (Hong
et al., 2009). A concept hierarchy is a kind of
concise and general form of concept description that
organizes relationships of data.
In this study, a hierarchical rough set (HRS)
problem is defined as follows: Given a decision
table data with hierarchical decision attributes, one
could induct decision rules from the reducts, the
minimal subset of attributes that enables the same
classification of elements of the universe as the
whole set of attributes in each corresponding object.
The reduct has the highest strong index (SI).
The objective of this study is to develop a
95
Huang C., Lin S., Chen Z. and Wang Y..
A Rule Induction with Hierarchical Decision Attributes.
DOI: 10.5220/0004410900950102
In Proceedings of the 15th International Conference on Enterprise Information Systems (ICEIS-2013), pages 95-102
ISBN: 978-989-8565-59-4
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

solution approach to resolve the HRS problem based
on AREA and characterized:
1) Induct a reduct that is the minimal subset of
attributes that enables the same classification of
elements of the universe as the whole set of
attributes.
2) Present a revised strength index to identify
meaningful reducts from all reducts, rather than
from the same number of attributes selected in the
reducts.
3) Explore the most specific decision attribute level
by level in the level-search procedure.
The paper is outlined as follows: Section 2 surveys
the literature related to rough set theory. Section 3
proposes the solution approach and section 4
concludes this study.
2 LITERATURE REVIEW
Rough sets theory has often proved to be an
excellent mathematical tool for analyzing a vague
description of objects (called actions in decision
problems). The adjective “vague”, refers to the
quality of information and means inconsistency or
ambiguity which follows from information
granulation (Pawlak, 1982). In the Rough Set (RS)
Theory, a reduct is the minimal subset of attributes
enabling the same classification of elements of the
universe as the whole set of attributes. In the RS
theory, attributes are classified into two sets:
condition and decision attributes. The second one
refers to the outcomes of the data set. Rough sets
theory has often proved to be an excellent
mathematical tool for analyzing a vague description
of objects (called actions in decision problems). The
adjective “vague”, refers to the quality of
information and means inconsistency or ambiguity
which follows from information granulation
(Pawlak, 1982; 1991).
Over the past years, the RS theory has indeed
become a topic of great interest to researchers and
has been applied to many areas, for example,
environmental performance evaluation (Chèvre et
al., 2003); (Yang et al., 2011), machine tools and
manufacture (Jiang et al., 2006), industrial
engineering (Liu et al., 2007), integrated circuits
(Yang et al., 2007), medical science (Pattaraintakorn
and Cercone, 2008); (Salama, 2010), economic and
financial prediction (Chen and Cheng, 2012);
(Cheng et al., 2010); (Tay and Shen, 2002),
electricity loads (Pai and Chen, 2009),
meteorological (Peters et al., 2003), airline market
(Liou and Tzeng, 2010) customer relationship
management (Tseng and Huang, 2007),
transportation (Kandakoglu et al., 2009); (Léonardi
and Baumgartner, 2004); (Utne, 2009) and other
real-life applications (Lewis and Newnam, 2011);
(Sikder and Munakata, 2009); (Yeh et al., 2010).
This success is due in part to the following aspects
of RS theory: (i) Only the facts hidden in data are
analyzed, (ii) No additional information about the
data is required such as thresholds or expert
knowledge, and (iii) A minimal knowledge
representation can be attained (Jensen and Shen,
2004).
However, previous studies on rough sets focused
on finding certain rules and possible rules that a
decision attribute is in one level only and not
hierarchical. However, hierarchical attributes are
usually predefined in real-world applications and
could be represented by a hierarchy tree (Hong et al.,
2009). A concept hierarchy is a kind of concise and
general form of concept description that organizes
relationships of data. Tseng (2006) proposed an
approach to generate concept hierarchies for a given
data set with nominal attributes based on rough set.
Dong et al., (2002) presented the model and
approach for hierarchical fault diagnosis for
substation based on rough set theory. These
approaches not only improve the efficiency of the
discovery process, but also express the user's
preference for guided generalization. However, they
did not consider the decision attribute with different
values in a different level combination, for example,
outcome O1 at level 1, outcome O2 at level 2, and
O3 at level 2.
Moreover, traditional RS approaches cannot
produce rules containing preference order, namely,
cannot achieve more meaningful and general rules
(Sun et al., 2005). RS based induction often
generates too many rules without focus and cannot
guarantee the classification of a decision table is
credible. For example, generation of classification
rules in Hassanien (2004), information-rich data to
reduce the data redundancy in Jensen and Shen
(2004), the analysis of diabetic databases in Breault
(2001), an unsupervised clustering in Questier et al.,
(2002), discovery of statistical significance rules in
Yin et al., (2001), an algorithm to infer rules in
Phuong et al. (2001).
New approaches, e.g., Tseng (2008) proposed a
new RS method, called alternative rule extraction
algorithm (AREA) to discover preference-based
rules according to the reducts with the maximum
strength index (SI), which is introduced to identify
meaningful reducts. However, these approaches used
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
96

two stages to generate reducts and induct decision
rules, respectively. Large computing space is
required to store the reducts from the first stage, and
solution searching is complex. Moreover,
comparison of the reducts using SI is limited to the
same number of condition attributes which are
selected in the reducts.
Next, a hierarchical decision rule induction
algorithm was proposed to solve the hierarchical
rough set (HRS) problem defined in section 3.
3 SOLUTION APPROACH
The hierarchical rough set problem is defined in this
section first. The concept of the hierarchy
framework is introduced and three axioms are
presented to show how the optimal level decision
rules are reached. The hierarchical decision rule
induction algorithm (HDRIA) is proposed to find the
decision rules finally. The accuracy and the
coverage are presented for each decision rule by
HDRIA.
3.1 Hierarchical Rough Set (HRS)
Problem
In this study, the hierarchical rough set problem is
defined as:
Given:
1) A hierarchical transportation decision table I =
(U, A∪{d}), where U is a finite set of objects and A
is a finite set of attributes. The elements of A are
called condition attributes. d ∉ A is a distinguished
hierarchical decision attribute at different level.
2) A concept hierarchy (a tree or a lattice) Hk refers
to on a set of domains Ox,…,Oz:
Hksk:{Ox …Oz} → Hksk-1 → Hk1, where
Hksk denotes the set of concepts at the the skth
level, Hksk-1 denotes the concepts at one level
higher than those at Hksk , and Hk1
represents the top level denoted as “ANY”.
Objective:
Minimize the subset of U, in which the specific
decision attribute of decision rules (ri) is with the
highest Strong Index (SI) and maximal level
number.
Subject to the following four constraints:
1) A = C
D,
2) B
C
3) POSB(D) = {x
U: [x]B
D}
4) For any a
B of C, K (B, D) = K (C, D), and
K (B, D)
K(B-{a}, D), where, C is condition
domain and D is decision domain. Attribute a ∈ A,
set of its values. K(B, D) is the degree of
dependency between B and D.
))D(POS(card
))D(POS(card
)D,B(K
C
B
POSB(D) is the positive region and includes all
objects in U which can be with classified into classes
of D, in the knowledge B.
3.2 The Structure of the Concept
Hierarchies
Notation:
O: a decision attribute set;
k: decision attribute hierarchical index;
l: level index;
e: entry point;
Hk: the concept hierarchy corresponding to O;
Hkl: the concept hierarchy corresponding to O at
level l;
sk: number of levels in the Hk;
Suppose that a concept hierarchy Hk refers to on a
set of domains Ox,…,Oz. Hksk:{Ox ×…×Oz} →
Hksk-1 → Hk1, where Hksk denotes the set of
concepts at the skth level, Hksk-1 denotes the
concepts at one level higher than those at
Hksk , Hk1 represents the top level denoted as
“ANY”, Ox refers to the value of attribute = x at
level 1, Ox.y refers to the value of attribute = x at
level 1 and y at level 2, and Ox.y.z refers to
the value of attribute = x at level 1, y at level 2, and
z at level 3, …, etc.
Ox.y.z ∈ Ox.y ∈ Ox implies that more level, more
specific information. And, in the concept tree, Ox is
father node of Ox.y. Ox.y is a son node of Ox. Ox.y
and Ox.n are brother node for each other.
Figure 1: An example of Concept Tree.
In the concept tree, the most general concept can
be a universal concept, whereas the most specific
concepts correspond to the specific values of
attributes in the data set. Each node in the tree of
ARuleInductionwithHierarchicalDecisionAttributes
97
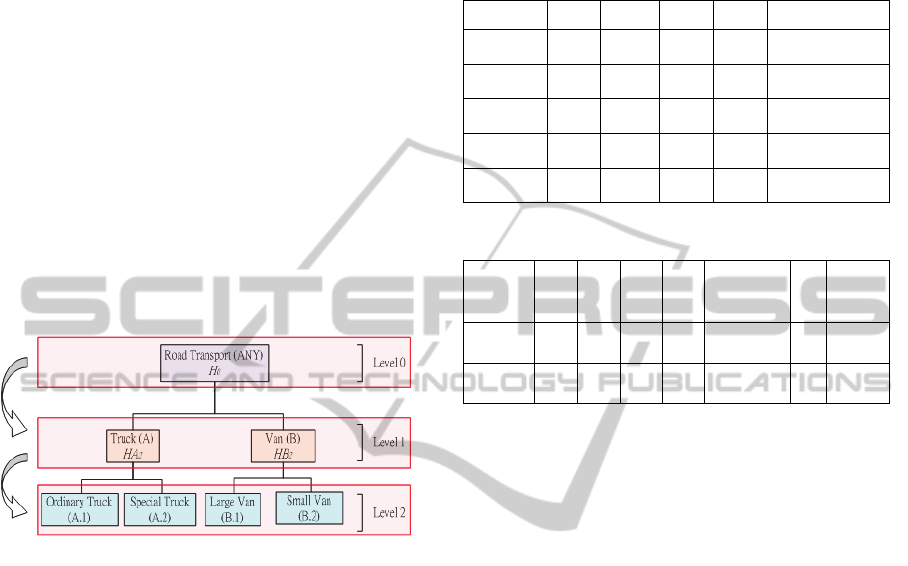
concept hierarchy represents a concept
transportation hierarchy. In Fig. 1, for example,
OA.1 ∪ OA.2 = HA2 ∈ OA, OB.1 ∪ OB.2 =
HB2 ∈ OB, OA ∪ OB = H1 ∈ O0.
3.3 The Level-search Procedure
Three axioms are supported to show how the final
decision rules are reached. Initially, the default entry
point for hierarchical decision attribute (outcome) is
at the top level (e =1). Then the level-search
procedure explores down level until violation from
the axioms to stop further exploration. The final
decision rules are induct.
For example, in Fig. 2, the decision rule’s
outcome at Level 2 (OA.2 = the special truck) is
more informative than Level 1 (OA = truck). The
procedure will explore level 2 if no any violation in
three axioms.
Figure 2: Concept hierarchies search process.
The three axioms are proposed as follows:
Notations:
O: a decision attribute (outcome) set;
k: the decision attribute hierarchical index;
L: level of concept hierarchy;
l: level index;
Ck: the node of outcome Ok in the concept
hierarchy
Hkl.
Axiom 1: Ll is more informative than Ll-1
Axiom 2: For the node Ck in the hierarchy tree,
outcome of each Ck’s children nodes ∉ outcomes
of all current decision rule set, stop explore.
Axiom 3: Stop exploring node Ck if two conditions
are met: (1) its outcome Ok ∈ outcomes in current
decision table, but ∉outcome of the current
decision rule set. (2) Outcomes in its brother node ∈
outcomes in current decision table, and ∈outcomes
of the current decision rule set.
For example, given a decision table in Table I, The
outcomes are explored at level 2. There are three
outcomes (1.1, 1.2, and 2.1). The data of the level 2
decision table are exemplified in Table I. Apply the
RS approach and explore at a node C1, the current
decision rule set is obtained in Table II.
Table 1: The level 2 decision table.
Object A1 A2 A3 O Cardinal number
1 1 2 2 1.1 10
2 2 2 1 1.1 10
3 2 2 1 1.2 10
4 1 1 1 2.1 10
Wj 0.1 0.4 0.2
Table 2: The level 2 decision rule set.
Rule NO A1 A2 A3 O
Object
Cardinality
SI
Support
Object
1
2 1.1 10 2 1
2
1
2.1 10 4 4
Object 3 has the outcome O
1.2
in the decision
table but not in the current decision rule set.
Moreover, the outcome O
1.2
who has brother
outcome O
1.1
is in the decision table and also in the
decision rule. Then, stop exploring node C
1
. In this
case, since two outcomes of brother nodes conflict to
each other (i.e. one of them is not in the decision set),
the procedure will stop at their father node.
3.4 The Hierarchical Decision Rule
Induction Algorithm (HDRIA)
The main idea of the HDRIA is to select an object to
entry. Then set the default entry point e = L1 and
CANCk = GO. Based on DREA in Section II-A,
find the set of decision rules for each object. For
each note Ck, if CANCk = GO then check:
According to Hkl, if all outcomes of decision table ∈
outcomes of the current decision rule set, based on
Axiom 1, then explore next level.
According to Hkl, if all outcomes of decision table
∉ in outcome of decision rule, based on Axiom 2,
then stop exploring this node.
According to Hkl, if the node Ckl whiose outcomes
(Ok) in the Hkl corresponding decision table ∉
outcomes of the current decision rule set, but there
is another brother note Ck’l whose outcome (Ok’) of
the corresponding decision table ∈ the current
decision rule set, then based on Axiom 3, stop
exploring Ckl. And go exploring its brother node,
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
98

Ck’l.
If Ckl has no more low level, then stop explore,
otherwise repeat these steps until no more node to
explore.
In the AREA proposed by Tseng (2008), the strength
index of reduct f is computed as SI(f) =
m
j 1
v
j
W
j
* n
f.
The weakness of the that SI(f) is the comparison of
the reducts is limited to the same decision attribute
and to same number of attributes selected in the
reducts. While number of attributed involved is
more, the SI(f) is larger, which conflicts with the
objective of an attribute reduct which is a minimal
subset of attributes that provides the same
descriptive ability as the entire set of attributes. In
the other words, attributes in a reduct is jointly
sufficient and individually necessary (Yao and Zhao,
2009). Therefore, the SI(f) is revised and refers to as
follows:
SI(f) =
m
j 1
m
j 1
(1)
where: f is the reduct index, f = 1, ..., n;
v
j
= 1 if condition attribute j is selected,
0 otherwise (A
j
= “x”);
W
j
is the weight of condition attribute j;
n
f
is the number of identical reducts f;
The hierarchical decision rule induction algorithm
(HDRIA) is presented as follow:
Notation:
e: entry point;
L: level of concept hierarchy;
l:l evel index;
O: a decision attribute set;
k: decision attribute hierarchical index;
Hk: the concept hierarchy corresponding to Ok;
Hkl: the concept hierarchy corresponding to Ok
at level
l;
Ckl: the node of outcome Ok in the concept
hierarchy
Hkl;
CAN
: an option GO or NG for Ckl. GO means
can go
to next level. NG means stop;
r: node index;
sk: number of levels in the Hk;
sr: number of Ckl;
Input: the decision table
Output: the decision rule set
Step 0 Initialization
Select the block of the data need to
analysis.
Set the default entry point e = L1.
Set
= GO
Step 1 Based on Axiom 1
For l = 1 to sk+1
Apply DRIA to find the decision rule
set
For r = 1 to sr
If CAN
= GO
If all Hk
l
outcomes of decision table ∈
outcomes of all decision rules then set
← GO
End if
If all Hk
l
outcomes of decision table ∉ outcome
of decision rule
Based on Axiom 2, then set
← NG
End if
If node Ck
l
in Hk
l
outcome (O
k
) of decision table
∉ outcome of decision rule, but other node Ck
l
in
Hk
l
outcome (O
k’
) of decision table ∈ the
decision rule set, then based on Axiom 3, set
← NG,
← GO
Endif
Else If node Ck
l
no more relatively low level,
then Ck
l
= Ck
l-1
and
← NG
End if
End if
Else if
= NG, then Stop;
End for
End for
Step 2 Termination: Stop and output the results.
3.5 Validation of HDRIA
In order to validate the accuracy and coverage of
HDRIA, two performance measures are introduced:
accuracy index, coverage index. Accuracy index
α
D
and coverage index ψ
D
are defined as
following (Tsumoto, 1998):
|
∩
|
|
|
, and 0
1
|
∩
|
|
|
, and 0
1
where: |A| denotes the cardinality of set A, α
D
denotes the accuracy of R (e.g., eij = vij, in a
decision table) as to categorization of D, and ψ
D
denotes a coverage, respectively.
The accuracy (ac) and the coverage (co) of the
ARuleInductionwithHierarchicalDecisionAttributes
99

example (data in Table I and concept tree in Fig. 1)
are computed. The comparison between the optimal
level and all in top, 2
nd
, 3
rd
, and all in lowest levels
by HDRIA is presented in Table III. In Table III, the
coverage is the worst at the top level (the traditional
RS approaches). And the result of the coverage is
the best at the optimal level (the proposed approach).
The proposed algorithm can reach a final rule set,
which shows:
All qualified decision rules can be found.
The optimal level outcome is specific.
The best accuracy and coverage for each rule.
Table 3: The accuracy and coverage.
Top
level
2
nd
level
3
rd
level
The lowest
level
Optimal
level
Rule No. ac co ac co ac ac ac co ac co
1 0.5 0.33 1 1 1 1 1 1 1 1
2 1 0.67 1 1 1 1 1 1 1 1
3 1 0.5 1 0.5 1 1 - - 1 1
4 1 0.5 - - - - - - 1 1
Number of
rules
4 3 3 2 4
*Note: the lowest level refers that all outcomes are the specific in
the decision table.
The complexity of AREA and REA are
compared in Table IV. The results shows that REA
is more efficient since complexity of traditional RS
approach is O(n
4
) (Reduct Generation) + 3
(REA). Complexity of REA algorithm is O(n
4
)
and HDRIA is 1
2
Table 4: The complexity of the proposed algorithms and
the original algorithms.
Algorithm Description Time complexity in the worst case
Reduct
Generation
Generate the reduct
from the decision
table.
AREA
Extract the decision
rule from the
reduct.
3
DRIA
Induct the decision
rule from the
decision table.
2
HDRIA
Find the final level
by DRIA
1
2
where
n: total number of objects;
m: total number of attributes;
r: total number of reducts;
R: total number of decision rules;
sk: total number of levels;
4 CONCLUSIONS AND FUTURE
WORK
This study considered the hierarchical attributes that
are usually predefined in real-world applications by
a concept hierarchy concept tree. This study aimed
the decision maker to solve the hierarchical rough
set (HRS) problem and with the following
contribution:
1) Presented a revised strength index to identify
meaningful reducts from all reducts, rather than
from same number of attributes selected in the
reducts.
2) The (HDRIA) algorithm was proposed to
explore the decision rules of the hierarchical
decision attributes in different levels combination.
In the future, the condition attributes may consider
hierarchy concept, too. The extension to other
industry involving in the hierarchical and qualitative
data analysis is required. Also, a practical case will
be studied: The ABC company established in 1954
owns a fleet over 3000 vehicles, including trucks
and vans in different sizes. The fleet can be
developed in a hierarchy concept. The company
plans the daily scheduling that requires allocating
different types of vehicles according to different
routes. The solution is influenced by several factors,
including environmental regulations, which affect
the determination of the ratio of green vehicles in the
fleet. The ratio is a crucial reference in purchasing
new fleets. In this case study, selection of the
transportation fleet and determine the ratio is
undoubtedly the urgent problem that the ABC
company faces. Applying the proposed solution
approach to induct decision rules will aim resolving
the problem and enhancing the agility of decision
making.
REFERENCES
Breault, J. L., 2001. Data mining diabetic databases: are
rough sets a useful addition? Proceedings of the
Computing Science and Statistics, 33.
Chèvre, N., Gagné, F., Gagnon, P., and Blaise, C., 2003.
Application of rough sets analysis to identify polluted
aquatic sites based on a battery of biomarkers: a
comparison with classical methods. Chemosphere,
51(1), p.13-23.
Chen, Y. S., and Cheng, C. H., 2012. A soft-computing
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
100

based rough sets classifier for classifying IPO returns
in the financial markets. Applied Soft Computing,
12(1), p.462-475.
Cheng, C. H., Chen, T. L., and Wei, L. Y., 2010. A hybrid
model based on rough sets theory and genetic
algorithms for stock price forecasting. Information
Sciences, 180(9), p.1610-1629.
Dong, H., Zhang, Y., and Xue, J., 2002. Hiearchical fault
diagnosis for substation based on rough set.
Proceedings of the Power System Technology, 4,
p.2318–2321.
Hong, T. P., Liou, Y. L., and Wang, S. L., 2009. Fuzzy
rough sets with hierarchical quantitative attributes.
Expert Systems with Applications, 36(3, Part 2),
p.6790-6799.
Hassanien, E., 2004. Rough set approach for attribute
reduction and rule generation: a case of patients with
suspected breast cancer. Journal of the American
Society for Information Science and Technology,
55(11), p. 954–962.
Jiang, Y. J. Chen, J. and Ruan, X. Y., 2006. Fuzzy
similarity-based rough set method for case-based
reasoning and its application in tool selection.
International Journal of Machine Tools and
Manufacture, 46(2), p.107-113.
Jensen R. and Shen, Q., 2004. Fuzzy–rough attribute
reduction with application to web categorization,
Fuzzy Sets and Systems, 141(3), p.469-485
Kandakoglu, A., Celik, M., and Akgun, I., 2009. A
multi-methodological approach for shipping registry
selection in maritime transportation industry.
Mathematical and Computer Modelling, 49(3–4),
p.586-597.
Liou, J. J. H., and Tzeng, G. H., 2010. A
Dominance-based Rough Set Approach to customer
behavior in the airline market. Information Sciences,
180(11), p.2230-2238.
Liu, M., Shao, M., Zhang, W., and Wu, C., 2007.
Reduction method for concept lattices based on rough
set theory and its application. Computers Mathematics
with Applications, 53(9), p.1390-1410.
Léonardi, J., and Baumgartner, M., 2004. CO2 efficiency
in road freight transportation: Status quo, measures
and potential. Transportation Research Part D:
Transport and Environment, 9(6), p.451-464.
Lewis, I., and Newnam, S., 2011. The development of an
intervention to improve the safety of community care
nurses while driving and a qualitative investigation of
its preliminary effects. Safety Science, 49(10),
p.1321-1330.
Pawlak, Z., 1982. Rough Sets. International Journal of
Computer and Information Sciences, 11(5), p. 341-356
Pawlak, Z., 1991. Rough Sets: Theoretical Aspects of
Reasoning about Data. Kluwer Academic Publishers,
Boston.
Pai, P. F., and Chen, T. C., 2009. Rough set theory with
discriminant analysis in analyzing electricity loads.
Expert Systems with Applications, 36(5), p.8799-8806.
Peters, J. F., Suraj, Z., Shan, S., Ramanna, S., Pedrycz, W.,
and Pizzi, N., 2003. Classification of meteorological
volumetric radar data using rough set methods.
Pattern Recognition Letters, 24(6), p.911-920.
Pattaraintakorn, P., and Cercone, N., 2008. Integrating
rough set theory and medical applications. Applied
Mathematics Letters, 21(4), p.400-403.
Phuong, N. H., Phong, L. L., Santiprabhob P. and Baets,
B. De., 2001. Approach to generating rules for expert
systems using rough set theory. Proceedings of IEEE
International Conference on IFSA World Congress
and 20th NAFIPS, Vancouver, BC, Canada, 2,
p.877–882.
Questiera, F., Arnaut-Rollier, I., Walczak B. and Massart,
D. L., 2002. Application of rough set theory to feature
selection for unsupervised clustering. Chemometrics
and Intelligent Laboratory Systems, 63(2), p.155–167.
Sun, C. M., Liu, D. Y., Sun, S. Y., Li, J. F. and Zhang, Z.
H., 2005. Containing order rough set methodology.
Proceedings of 2005 International Conference on
Machine Learning and Cybernetics, Guangzhou,
China, 3, p.1722–1727.
Sikder, I. U., and Munakata, T., 2009. Application of
rough set and decision tree for characterization of
premonitory factors of low seismic activity. Expert
Systems with Applications, 36(1), p.102-110.
Tsumoto, S., 1998. Automated extraction of medical
expert system rules from clinical databases based on
rough set theory. Information Sciences, 112(1–4),
p.67-84.
Tseng, T. L., Huang, C. C., Jiang, F., and Ho, J. C., 2006.
Applying a hybrid data mining approach to prediction
problems: A case of preferred suppliers prediction,
International Journal of Production Research, 44(14),
p.2935-2954.
Tseng, T. L., Huang, C. C., 2007. Rough set-based
approach to feature selection in customer relationship
management. Omega, 35(4), p.365-383.
Tseng, T. L. B., Huang C. C. and Ho, J. C., 2008.
Autonomous Decision Making in Customer
Relationship Management: A Data Mining Approach.
Proceeding of the Industrial Engineering Research
2008 Conference, Vancouver, British Columbia,
Canada.
Tay, F. E. H., and Shen, L., 2002. Economic and financial
prediction using rough sets model. European Journal
of Operational Research, 141(3), p. 641-659.
Thangavel, K. and Pethalakshmi, A., 2009.Dimensionality
reduction based on rough set theory: A review Article,
Applied Soft Computing, 9(1), p.1-12.
Utne, I. B., 2009. Life cycle cost (LCC) as a tool for
improving sustainability in the Norwegian fishing fleet.
Journal of Cleaner Production, 17(3), p.335-344.
Yin, X., Zhou, Z., Li, N. and Chen, S., 2001. An Approach
for Data Filtering Based on Rough Set Theory.
Lecture Notes in Computer Science, 2118, p. 367-374.
Yeh, C. C., Chi, D. J., and Hsu, M. F., 2010. A hybrid
approach of DEA, rough set and support vector
machines for business failure prediction. Expert
Systems with Applications, 37(2), p.1535-1541.
Yao, Y. and Zhao Y., 2009. Discernibility matrix
ARuleInductionwithHierarchicalDecisionAttributes
101

simplification for constructing attribute reducts.
Information Sciences, 179(7), p.867-882.
Yang, M., Khan, F. I., Sadiq, R., and Amyotte, P., 2011. A
rough set-based quality function deployment (QFD)
approach for environmental performance evaluation: a
case of offshore oil and gas operations. Journal of
Cleaner Production, 19(13), p.1513-1526.
Yang, H. H., Liu, T. C., and Lin, Y. T., 2007. Applying
rough sets to prevent customer complaints for IC
packaging foundry. Expert Systems with Applications,
32(1), p.151-156.
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
102
