Are Multi-way Joins Actually Useful?
Michael Henderson and Ramon Lawrence
Department of Computer Science, University of British Columbia Okanagan, Kelowna, BC, Canada
Keywords:
Multi-way Join, Hybrid Hash, Join Ordering, Query Optimization, PostgreSQL.
Abstract:
Multi-way joins improve performance by avoiding extra I/Os from multiple partitioning steps. There are
several multi-way join algorithms proposed, and the research results are encouraging. However, commercial
database systems are not currently using multi-way joins. Practical issues include modifying the optimizer
and execution system to support multi-way operators and ensuring robust and reliable performance. The
contribution of this work is an implementation and experimental evaluation of multi-way joins in PostgreSQL.
We provide algorithms that modify the optimizer to cost multi-way joins and create and execute query plans
that have more than two input operators. Experimental results show that multi-way joins are beneficial for
several queries in a production database system and can be effectively exploited by the optimizer, however
there are implementation issues that must be resolved to guarantee robust performance.
1 INTRODUCTION
There has been recent research on the development
of multi-way join algorithms that are capable of join-
ing more than two relations at a time. Despite the
potential performance benefits, database systems are
not using multi-way joins. The objective of this paper
is to attempt to answer the question: Are multi-way
joins useful in database systems?
The positive argument for multi-way joins is sup-
ported by a significant amount of research literature
that demonstrates performance benefits. Hash teams
(Graefe et al., 1998a) implemented in Microsoft SQL
Server 7.0 and generalized hash teams (Kemper et al.,
1999) improve I/O efficiency compared to binary
plans by avoiding multiple partitioning steps. These
algorithms can be used for joins of relations on the
same join attributes (hash teams) or join relations re-
lated by a chain of functional dependencies/foreign
keys (generalized hash teams). It has been shown by
the SHARP (Bizarro and DeWitt, 2006) query pro-
cessing system that a multi-way operator adapts to es-
timation inaccuracies, has the ability to dynamically
share memory easier than binary plans, and avoids
redundant next() calls in the iterator model. Fur-
ther, streaming multi-way joins such as MJoin (Viglas
et al., 2003) and slice join (Lawrence, 2008) compen-
sate for network delays and blocking. A streaming
multi-way join operator allows tuples to be processed
from any input at any time which simplifies optimiza-
tion issues such as join order selection and handles
changing input arrival rates.
However, there are issues with robustness of
multi-way operators. A multi-way operator still must
select a probe ordering internally which has similar
complexity as join order selection with the additional
goal that it is adaptable to the data characteristics dur-
ing join processing. The one known commercial im-
plementation, hash teams in Microsoft SQL Server
7.0 (Graefe et al., 1998b), was later dropped in SQL
Server 2000 SP1 (Microsoft Corporation, 2001) in
order to improve stability and due to limited perfor-
mance benefits. There are limitations on the types of
joins possible using a multi-way operator. Hash teams
are limited to joins of relations all on the same join
attributes, generalized hash teams support chains of
foreign key joins, and SHARP supports star queries.
Finally, although it has been argued that the changes
to the query optimizer to support multi-way joins are
straightforward, in practice that is not the case. A typ-
ical query optimizer (Moerkotte and Neumann, 2008)
is only capable of exploring binary plans. Without
modifying the plan generator to cost multi-way plans
simultaneously with binary plans, multi-way opera-
tors must be constructed after binary optimization is
complete.
To gain insights on the capability of multi-way
joins in a database system, we implemented three
multi-way join algorithms: hash teams, generalized
hash teams, and SHARP. We have developed vari-
ous implementations of generalized hash teams and
examined their tradeoffs. A new post-optimization
13
Henderson M. and Lawrence R..
Are Multi-way Joins Actually Useful?.
DOI: 10.5220/0004412100130022
In Proceedings of the 15th International Conference on Enterprise Information Systems (ICEIS-2013), pages 13-22
ISBN: 978-989-8565-59-4
Copyright
c
 2013 SCITEPRESS (Science and Technology Publications, Lda.)

method for creating multi-way join plans takes as in-
put an optimized binary query plan and applies trans-
formations and costing to determine if a multi-way
plan is more efficient than the input binary plan.
The experimental test bed is PostgreSQL. Post-
greSQL is an open-source database system that
closely follows conventional practice. PostgreSQL
has an iterator-based execution model, cost-based op-
timizer, and an implementation of hybrid hash join.
Queries with multi-way joins show performance ben-
efits over binary hash joins in many cases. The per-
formance improvements vary by query type and im-
plementation approach. In general, multi-way algo-
rithms are faster as they perform fewer I/Os, but im-
plementations must avoid increasing the CPU time
for probing and join clause evaluation. The post-
optimization method implemented finds a significant
number of the beneficial plans, has insignificant run-
time cost, and requires minimal modifications to the
optimizer.
The contributions of this paper are:
• Implementations of the current state-of-the-art
multi-way join algorithms.
• Experimental analysis of some implementations
of generalized hash teams.
• A post-optimization algorithm for converting an
optimized binary plan into a multi-way execution
plan.
• An experimental evaluation of all algorithms in
the production database system PostgreSQL.
The organization of this paper is as follows. In
Section 2, we briefly overview existing work on
multi-way hash joins. The implementation of gen-
eralized hash teams is described in Section 3. The
post-optimization algorithm for constructing multi-
way plans is described in Section 4. The issues in
implementing the join algorithms in PostgreSQL are
covered in Section 5. Experimental results in Sec-
tion 6 demonstrate benefits but also implementation
challenges of multi-way joins. The paper closes with
conclusions and future work.
2 PREVIOUS WORK
This section contains background information on bi-
nary and multi-way hash join algorithms.
2.1 Binary Hash Joins
A join combines two relations into a single relation.
We refer to the smaller relation as the build relation,
and the larger relation as the probe relation. A hash
join first reads the tuples of the build relation, hashes
them on the join attributes to determine a partition in-
dex, and then writes the tuples to disk based on the
partition index. It then repeats the process for the
probe relation. The partitioning is designed such that
each build partition is now small enough to fit in a
hash table in available memory. This hash table is
then probed with tuples from the matching probe par-
tition. Hybrid hash join (HHJ) (DeWitt et al., 1984) is
a common hash join algorithm implemented in most
database systems. Hybrid hash join selects one build
partition to remain memory-resident before the join
begins. Any available memory beyond what is needed
for partitioning is used to reduce the number of I/O
operations performed. Dynamic hash join (DHJ) (De-
Witt and Naughton, 1995; Kitsuregawa et al., 1989)
can adapt to memory changes by initially keeping all
build partitions in memory and then flushing on de-
mand as memory is required. Hash join optimizations
(Graefe, 1992) include bit vector filtering and role re-
versal.
Skew occurs in data when certain values occur
more frequently than others. Skew can be classified
(Walton et al., 1991) as either partition skew or intrin-
sic data skew. Partition skew is when the partitioning
algorithm constructs partitions of non-equal size (of-
ten due to intrinsic data skew but also due to the hash
function itself). Partition skew can be partially mit-
igated by using many more partitions than required,
as in DHJ (Kitsuregawa et al., 1989; Nakayama et al.,
1988), and by producing histograms on the data when
recursive partitioning is required.
2.2 Multi-way Joins
A multi-way join can join two or more relations at
the same time. The common issues in all multi-way
join implementations are the hash table structure, the
probe ordering, and the join types supported.
The hash table structure must support the ability
to partition the input relations such that only tuples at
the same partition index can join together. Each input
typically has its own hash table and associated parti-
tion file buffers. A multi-way operator that has multi-
ple hash tables can use the memory available to buffer
tuples from any input. Internally, the algorithm must
select a probe ordering. The probe ordering specifies
the order of inputs to probe given a tuple of one in-
put. The probe ordering may differ based on the input
tuple and may adapt as the join progresses.
Not all joins can be efficiently executed using
multi-way hash joins. If all inputs cannot fit in mem-
ory, the only join plans that can be executed using one
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
14

partitioning step are those where the inputs all have
common hash attributes or joins where indirect parti-
tioning is possible. One partitioning step is sufficient
as the cleanup can be performed by loading all parti-
tions at the same index in memory and then probing.
Star joins can be processed using multi-dimensional
partitioning. Multi-dimensional partitioning requires
the build relations be read multiple times during the
cleanup phase, but this still may be more efficient than
the corresponding binary plans. The rest of this sec-
tion provides background on existing multi-way join
implementations.
2.2.1 Hash Teams
Hash teams (Graefe et al., 1998a) used in Microsoft
SQL Server 7.0 perform a multi-way hash join where
the inputs share common hash attributes. A hash
team consists of hash operators and a team manager
that coordinates the memory management for all in-
puts. Performance gains of up to 40% were reported.
The probe ordering is the same as the original binary
plan. The team manager is separate from the regu-
lar plan operators. The operators are binary and are
co-ordinated externally by the team manager.
2.2.2 Generalized Hash Teams
Hash teams were extended to generalized hash teams
(Kemper et al., 1999) that allows tables to be joined
using indirect partitioning. Indirect partitioning par-
titions a relation on an attribute that functionally de-
termines the partitioning attribute. A TPC-H (TPC,
2013) query joining the relations Customer, Orders,
and LineItem can be executed using a generalized
hash team that partitions the first two relations on
custkey and probes with the LineItem relation by us-
ing its orderkey attribute to indirectly determine a par-
tition number using a mapping constructed when par-
titioning Orders. This mapping provides a partition
number given an orderkey.
The major issue with indirect partitioning is that
storing an exact representation of the mapping func-
tion is memory-intensive. In (Kemper et al., 1999),
bitmap approximations are used that consume less
space but introduce the possibility of mapping errors.
These errors do not affect algorithm correctness but
do affect performance. The bitmap approximation
works by associating a bitmap of a chosen size with
each partition. A key to be stored or queried with the
mapping function is hashed based on the bitmap size
to get an index I in the bitmap. The bit at index I is
set to 1 in the bitmap for the partition where the tuple
belongs. Note that due to collisions in the hashing of
the key to the bitmap size, it is possible for a bit at
index I to be set in multiple partition bitmaps which
results in false drops. A false drop is when a tuple
gets put into a partition where it does not belong.
The generalized hash team algorithm does not
have a “hybrid step” where it uses additional mem-
ory to buffer tuples beyond what is required for parti-
tioning. Further, the bitmaps must be relatively large
(multiples of the input relation size) to reduce the
number of false drops. Consequently, even the bitmap
approximation is memory intensive as the number of
partitions increases.
2.2.3 SHARP
SHARP (Bizarro and DeWitt, 2006) is a multi-way
join algorithm for star joins that performs multi-
dimensional partitioning. An example TPC-H star
query involves Part, Orders and LineItem. In multi-
dimensional partitioning, Part and Orders are the
build tables and are partitioned on partkey and or-
derkey respectively. LineItem is the probe relation and
is partitioned simultaneously on (partkey,orderkey)
(in two dimensions). The number of partitions of the
probe table is the product of the number of partitions
in each build input. For example, if Part was par-
titioned into 3 partitions and Orders partitioned into
5 partitions, then LineItem would be partitioned into
5*3=15 partitions.
For a tuple to be generated in the memory phase,
the tuple of LineItem must have both its matching
Part and Orders partitions in memory. Otherwise,
the probe tuple is written to disk. The cleanup pass
involves iterating through all partition combinations.
The algorithm loads on-disk partitions of the probe
relation once and on-disk partitions of the build rela-
tion i a number of times equal to
∏
i−1
j=1
X
j
, where X
i
is the number of partitions for build relation i. Read-
ing build partitions multiple times may still be faster
than materializing intermediate results, and the opera-
tor benefits from memory sharing during partitioning
and the ability to adapt during its execution.
2.3 Other Join Algorithms
There are two other related but distinct areas of re-
search on join algorithms. There is work on paral-
lelizing main-memory joins based on hashing (Blanas
et al., 2011) and sorting (Albutiu et al., 2012). The as-
sumption in these algorithms is that there is sufficient
memory for the join inputs such that the dominate fac-
tor is CPU time rather than I/O time. In this work,
we are examining joins where I/O is still a major fac-
tor. The main-memory and cache-aware optimization
techniques employed in these works could also be ap-
plied to I/O bound joins.
AreMulti-wayJoinsActuallyUseful?
15

Another related area is performing multi-way
joins on Map-Reduce systems such as in (Zhang et al.,
2012; Afrati and Ullman, 2011). Map-Reduce sys-
tems are designed for very large-scale queries over a
commodity cluster. The join algorithms used and how
they apply to multi-way joins are distinct from tradi-
tional relational database systems.
3 IMPLEMENTING
HASH TEAMS
We have implemented several variations of general-
ized hash teams. All implementations support both
direct and indirect partitioning. The different imple-
mentation features can be classified in three areas:
• Partitioning - The standard generalized hash
team algorithm does not have a hybrid step. Our
implementation calculates the expected number
of partitions required and uses a multiple of this
number to partially compensate for skew. Dy-
namic partition flushing allows a “hybrid” com-
ponent to improve performance.
• Materialization - An algorithm may either
use lazy materialization of intermediate results
(Bizarro and DeWitt, 2006; Lawrence, 2008)
where no intermediate tuples are generated or ea-
ger materialization by generating all intermediate
tuples.
• Mapping - The algorithm uses either an exact
mapping or bit mapping for indirect partitioning.
These features are discussed in the following sec-
tions. This discussion only applies to the implemen-
tation of hash teams. The implementation of SHARP
is distinct and follows closely to (Bizarro and DeWitt,
2006) except that dynamic probe orderings and adap-
tive features are not implemented.
3.1 Partitioning
The partitioning algorithm must divide tuples such
that only tuples at the same partition index can join
together. The algorithm must also guarantee that for
each partition index the partitions for the N − 1 build
inputs can be memory resident at the same time dur-
ing cleanup in order to be probed by the probe input.
The minimum number of partitions (with lazy mate-
rialization), P
min
, required is:
P
min
=
∑
N−1
i=1
|R
i
| ∗ size(R
i
)
(M − overhead)
(1)
|R
i
| is the number of tuples of input R
i
, and
size(R
i
) is the average size in bytes of each tuple. M
is the join memory size in bytes and N is the total
number of inputs in the join. Overhead is the over-
head in bytes for mapping functions which consume
memory available for the join (details in Section 3.3).
The partitioning is done in order of increasing size of
the build relations. Determining a partition ordering
for indirect partitioning joins is similar except that a
partial ordering must be respected such that an input
cannot be partitioned before the input that generates
its mapping is partitioned. Consequently, the last re-
lation in the functional dependency chain (which we
refer to as the determinant relation) is always the last
partitioned relation.
Similar to DHJ (DeWitt and Naughton, 1995), the
number of partitions P is a multiple of the minimum
required (currently P = 4 ∗ P
min
). This will partially
compensate for skew and allow the in-memory parti-
tions to be determined dynamically. Additional parti-
tions and dynamic de-staging do not solve all partition
skew issues. Similar to binary joins, recursive parti-
tioning can be applied on a partition where all build
relations cannot fit in memory simultaneously.
3.2 Materialization
There are two approaches to generating output tu-
ples. Eager materialization builds intermediate tu-
ples for each binary join in the operator. When join-
ing the relations Customer, Orders, and LineItem, this
would result in materializing the intermediate rela-
tion Customer-Orders before probing with LineItem.
In general, eager materialization is not a good choice
because of the cost of generating the intermediate re-
lations. Further, partitioning becomes more difficult
as estimating the size of the intermediate relations
may be difficult, and they must fit in memory dur-
ing cleanup. The benefit is that the standard binary
join code can be used unchanged after partitioning is
complete, and every intermediate tuple is only mate-
rialized once.
With lazy materialization (Bizarro and DeWitt,
2006; Lawrence, 2008) pointers to the component tu-
ples are kept and only when all components tuples
are available is a result generated. Lazy materializa-
tion saves the cost of materializing intermediate tu-
ples and requires fewer partitions (and less risk of par-
tition skew) during partitioning. However, this is the
classic time versus space trade-off. Space is saved by
not materializing intermediate relations with a trade
off in time because a given combination of compo-
nent tuples may need to be generated multiple times.
For instance, a given pair of Customer and Orders tu-
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
16

ples with matching custkey is not materialized as in
a binary plan, however it must be rebuilt every time
for the corresponding LineItem tuples. Note that lazy
materialization is ideal for SHARP or one-to-one car-
dinality joins as the join would never materialize in-
termediate tuples more than once.
3.3 Mapping
Indirect partitioning requires the construction and use
of mappers that given an attribute in the relation being
indirectly partitioned return the partition where that
tuple belongs. In addition to the bit mapper proposed
in (Kemper et al., 1999), we implemented a simple
exact mapper. The exact mapper records an integer
hash value (or the join attribute if it is an integer key)
as a lookup value and the data value is the hash key
of the partitioning attribute. This reduces the number
of false drops to only instances of collisions of hash
values. The exact mapper is implemented as a hash
table. If a mapping lookup fails to find an entry, that
implies the mapping was never generated and the tu-
ple requesting the mapping can be discarded. Each
mapping occupies approximately 12 bytes of space (4
for lookup hash value, 4 for data hash value, and 4 for
pointer in hash table structure).
In certain cases, the exact mapper is more space
efficient than an array of bitmaps (one for each par-
tition) when the number of partitions increases. For
one indirect partitioning step, the percentage of false
drops (Kemper et al., 1999) for a bit mapper is
p−1
p
∗
t−1
b
where p is the number of partitions,t is the size in
tuples of the mapping generator relation, and b is the
length of the bitmap. The number of false drops in-
creases with the number of partitions p and is directly
proportional to the ratio of the mapping relation size
to the bitmap size. For a reasonable percentage of
false drops, the bitmap size must be 4 or 8 times the
number of tuples in the mapping relation.
Consider indirectly partitioning LineItem with a
mapping built from Orders.orderkey. Let t = 15 mil-
lion tuples of Orders and p = 8. Assume the bit vector
is 4 times the size of orders, i.e. b = 60 million bits.
Then the percentage of false drops is
7
8
∗
15
60
= 21.9%.
Since we need a bitmap for each partition, the total
mapping cost is p ∗ b = 480 million bits. An exact
mapper storing the hash value of Orders.orderkey for
lookup and a data member that is the hash value of
Orders.custkey would occupy 12 bytes of space (size
of two integers plus a pointer). Based on the previous
example, the cost of this mapper is 960 million bits
with no false drops. For p > 16, the exact mapping
consumes less space than the bitmap approach.
The mapper size limits the use of indirect parti-
tioning as the mapper must fit in memory to be worth-
while. Otherwise, the random I/Os incurred by map-
ping destroy any cost advantageof the multi-way join.
4 CONSTRUCTING
MULTI-WAY PLANS
USING POST-OPTIMIZATION
The post-optimization approach to create multi-way
join plans occurs after an optimized logical query tree
has been produced. During conversion into an exe-
cution plan, hash join nodes are examined to see if
they can be merged into multi-way join nodes with
their children. In the greedy algorithm in Figure 2,
a hash join node is considered for conversion into a
multi-way join node if one or both of its children are
either a binary hash join or a multi-way hash join. A
multi-way join is only created if all of the children of
the given node can be combined into a multi-way join
operator. Only three possibilities must be considered
(see Figure 1):
• Merge with left child hash node - The inputs are
the inputs of the left child and the right input.
• Merge with right child hash node - The inputs are
the inputs of the right child and the left input.
• Merge with both children hash nodes - The inputs
are all the inputs of both children.
Original Binary Plan
UTSR
R
S
U
T
SR
S
R
UT
Merge both children
U
T
Merge right child
Merge left child
Figure 1: Building a Multi-Way Join via Merging.
The method
buildNWayNode takes an array of
logical query tree input nodes and attempts to con-
struct a multi-way hash join execution node. The in-
puts are analyzed to see if they fall into the three query
types supported:
• Direct partitioning join - All inputs must have the
attributes required by the hash function.
• Indirect partitioning join - All inputs must have
the partitioning attributes or have attributes that
functionally determine the partitioning attributes.
AreMulti-wayJoinsActuallyUseful?
17

PlanNode* convertHashNode(HashNode *current)
// Given a HashNode in the logical query tree converts it into a
// binary or multi-way hash join plan (execution) node.
{
Node* left = current→getLeft();
Node* right = current→getRight();
int leftType = left→getType();
int rightType = right→getType();
double binaryCost = current→getCost();
double bestCost = binaryCost;
PlanNode* bestPlan = null;
NWayNode* nway;
if (leftType is binary or nway hash join)
{ // Merge with left child
nway = buildNWayNode(left.getChildren(),right);
if (nway != null)
if (nway→getCost() < bestCost)
{ bestPlan = nway;
bestCost = nway→getCost();
}
}
if (rightType is binary or nway hash join)
{ // Merge with right child
nway = buildNWayNode(left, right.getChildren());
if (nway != null)
if (nway→getCost() < bestCost)
{ bestPlan = nway;
bestCost = nway→getCost();
}
}
if (leftType and rightType are binary or nway hash joins)
{ // Merge with both children
nway = buildNWayNode(left.getChildren(), right.getChildren());
if (nway != null)
if (nway→getCost() < bestCost)
{ bestPlan = nway;
bestCost = nway→getCost();
}
}
if (bestPlan != null)
{ // One of the multi-way plans is better
Construct a multi-way join node for the logical query tree.
Update pointer in parent node to point to new multi-way join
node as we may do merge recursively.
return nway; // Return multi-way join execution node
}
Otherwise convert to binary hash join node as usual
}
Figure 2: Post-Optimization Multi-Way Join Algorithm.
• Star join - One of the inputs must be a relation that
joins with all the other inputs.
The approach to determine if a multi-way join is
possible is to start with a single join clause and iter-
atively add one join clause at a time and evaluate if
the join is still one of the three types supported. It is
possible for a join to be both a direct partitioning and
a star join. In that case, the direct partitioning join is
selected as it is more efficient.
The advantage of the post-optimization approach
is that it requires fewer modifications to the query
optimizer and can be performed in time linear with
the number of hash joins in the plan. The post-
optimization conversion replaces sequences of binary
joins with more efficient multi-way joins for execu-
tion but does not alter the query plan in any other
way. Thus, if the original binary plan is good, the
multi-way should be better if the multi-way operator
executes more efficiently than the sequence of binary
operators.
5 IMPLEMENTING MULTI-WAY
JOINS IN POSTGRESQL
Adding the multi-way join algorithms, generalized
hash teams and SHARP, involved the addition of six
source code files. Each join had a file defining its
hash table structure and operations and a file defining
the operator in iterator form. Generalized hash teams
(GHT) had two mapper implementations: exact map-
per and bit mapper.
In comparison to implementing the join algo-
rithms themselves, a much harder task was modifying
the optimizer and execution system to use them. The
basic issue is both of these systems assume a maxi-
mum of two inputs per operator, hence there are many
changes required to basic data structures to support a
node with more than two inputs. The changes can be
summarized as follows:
• Create a multi-way hash node structure for use in
logical query trees and join optimization planning.
• Create a multi-way execution node that stores the
state necessary for iterator execution.
• Modify all routines associated with the planner
that assume two children nodes including EX-
PLAIN feature, etc.
• Create multi-way hash and join clauses (quals)
from binary clauses.
• Create cost functions for the multi-way joins that
conform to PostgreSQL cost functions which in-
clude both I/O and CPU costs.
• Modify the mapping from logical query trees to
execution plan (specifically for hash join nodes
as given in Figure 2) to support post-optimization
creation of multi-way join plans.
The changes were made as general as possible.
However, there are limitations on what queries can be
successfully executed with multi-way joins.
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
18

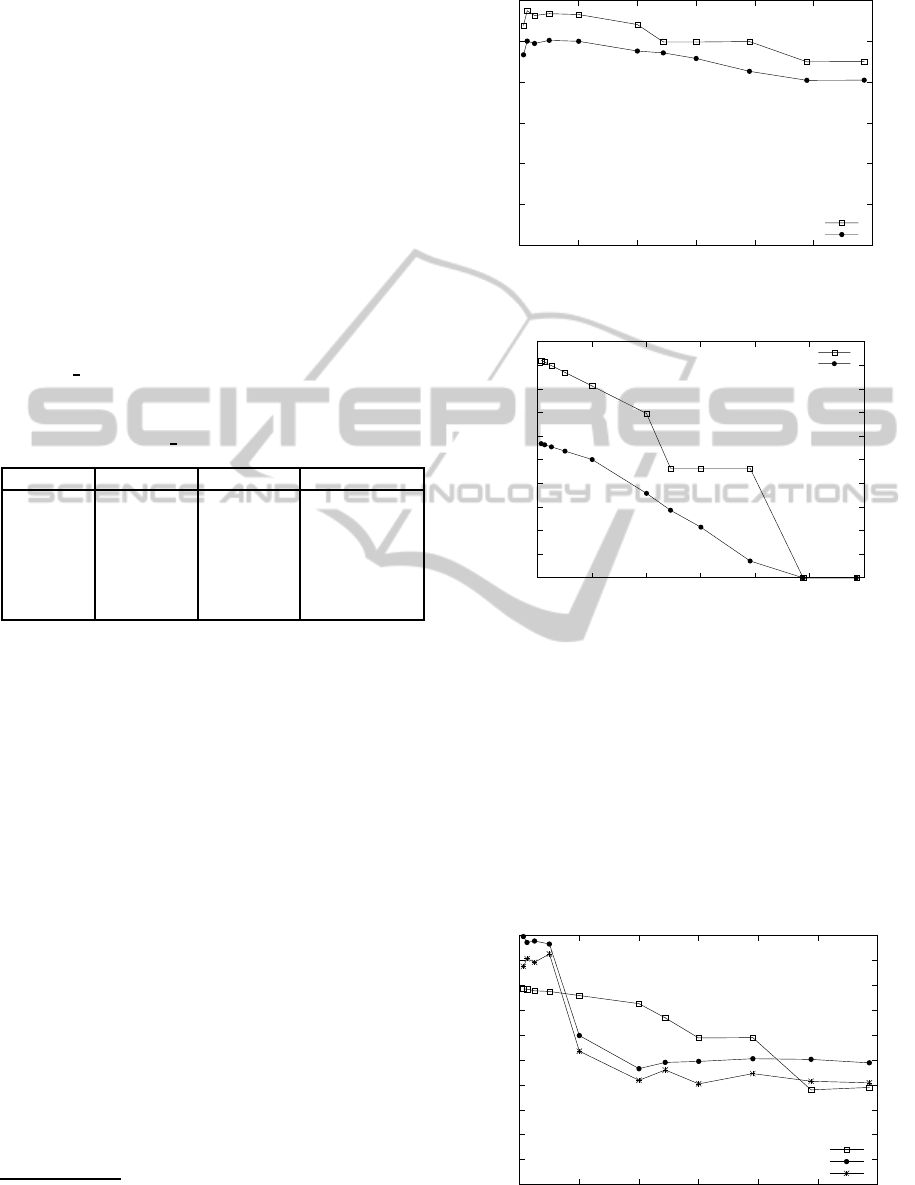
6 EXPERIMENTAL RESULTS
The experiments were executed on a dual proces-
sor AMD Opteron 2350 Quad Core at 2.0 GHz with
32GB of RAM and two 7200 RPM, 1TB hard drives
running 64-bit SUSE Linux. Similar results were
demonstrated when running the experiments on a
Windows platform. PostgreSQL version 8.3.1 was
used, and the source code modified as described.
The data set was TPC-H benchmark (TPC, 2013)
scale factor 10 GB
1
(see Figure 3) generated us-
ing Microsoft’s TPC-H generator (Chaudhuri and
Narasayya, ), which supports generation of skewed
data sets with a Zipfian distribution. The results
are for a skewed data set with z=1. Experiments
tested different join memory sizes configured using
the
work mem parameter. The memory size is given
on a per join basis. Multi-way operators get a multi-
ple of the join memory size. For instance, a three-way
operator gets 2*
work mem for its three inputs.
Relation Tuple Size #Tuples Relation Size
Customer 194 B 1.5 million 284 MB
Supplier 184 B 100,000 18 MB
Part 173 B 2 million 323 MB
Orders 147 B 15 million 2097 MB
PartSupp 182 B 8 million 1392 MB
LineItem 162 B 60 million 9270 MB
Figure 3: TPC-H 10 GB Relation Sizes.
6.1 Direct Partitioning
One experiment was a three-way join of Orders rela-
tions. The join was on the orderkey and produced 15
million results. The results are in Figure 4 (time) and
Figure 5 (IOs).
The results clearly show a benefit for a multi-way
join with about a 60% reduction in I/O bytes for the
join and approximately 12-15% improvement in over-
all time. The multi-way join performs fewer I/Os by
saving one partitioning step. It also saves by not ma-
terializing intermediate tuples in memory and by re-
ducing the number of probes performed. The multi-
way join continues to be faster even for larger mem-
ory sizes and a completely in-memory join.
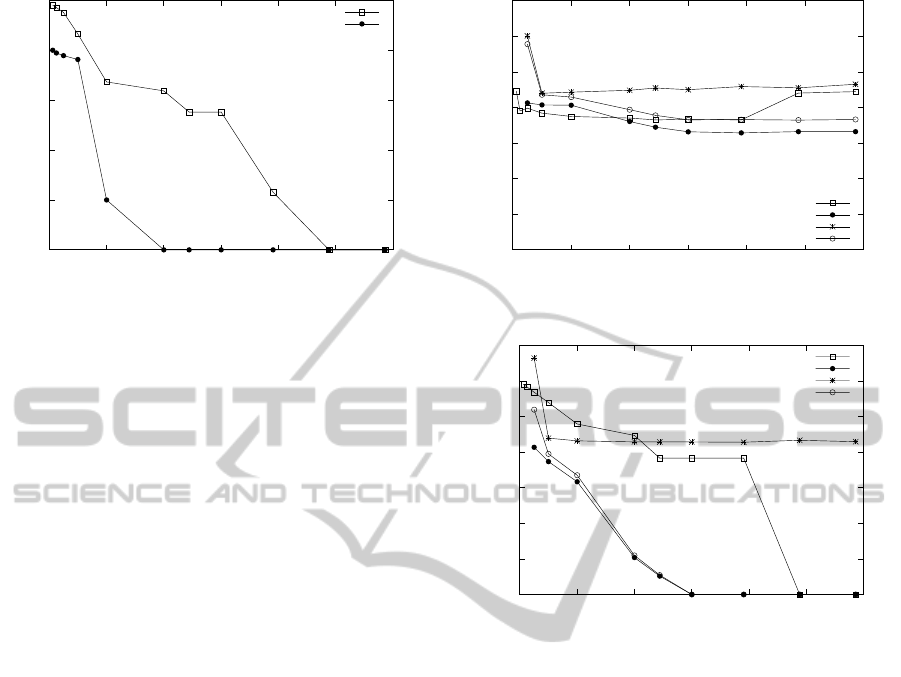
Another direct partitioning join hashes Part, Part-
Supp and LineItem on partkey and joins PartSupp and
LineItem on both partkey and suppkey. The results are
in Figure 6 (time) and Figure 7 (IOs).
Unlike the one-to-one join, this join exhibited dif-
ferent performance based on the implementations.
1
The TPC-H data set scale factor 100 GB was tested on
the hardware but run times of many hours to days made it
impractical for the tests.
0
50
100
150
200
250
300
0 500 1000 1500 2000 2500 3000
Time (sec)
Memory Size (MB)
HHJ
N-way (direct)
Figure 4: Three Way Orders Join (Time).
0
2000
4000
6000
8000
10000
12000
14000
16000
18000
20000
0 500 1000 1500 2000 2500 3000
I/Os (MB)
Memory Size (MB)
HHJ
N-way (direct)
Figure 5: Three Way Orders Join (I/O bytes).
The original implementation (not shown) had the
multi-way join being slower over all memory sizes
by 5-20% even though it had performed significantly
less I/O. The difference turned out to be significantly
more hash and join qualifier (clause) evaluations for
the multi-way operator. Several optimizations were
made to reduce the number of qualifier evaluations
and probes to below that of HHJ. The multi-way join
does not have superior performance over all memory
sizes. The major improvement in I/Os at 500 MB is
due to the multi-way operator sharing memory be-
500
520
540
560
580
600
620
640
660
680
700
0 500 1000 1500 2000 2500 3000
Time (sec)
Memory Size (MB)
HHJ
N-way (direct,lazy)
N-way (direct,eager)
Figure 6: Part-PartSupp-LineItem (Time).
AreMulti-wayJoinsActuallyUseful?
19

0
5000
10000
15000
20000
25000
0 500 1000 1500 2000 2500 3000
I/Os (MB)
Memory Size (MB)
HHJ
N-way (direct)
Figure 7: Part-PartSupp-LineItem (I/O bytes).
tween the inputs as the smaller input Part fits in its
500 MB allocation and can provide an extra 187 MB
to buffer PartSupp tuples.
To test the potential benefit of eager materializa-
tion, we modified the implementation to allow for ma-
terialization of intermediate tuples unconstrained by
memory limitations. Thus, the materialization imple-
mentation is unrealistically good as it could exceed
the space allocated for the join considerably without
paying any extra I/O or memory costs. The result was
only a 2% improvement in time.
The clear impact of probing cost on the results
motivate the benefit of adaptive probe orders which
may improve results. CPU costs are often consid-
ered a secondary factor to I/Os for join algorithms,
although in practice the costs can be quite significant.
6.2 Indirect Partitioning
Indirect partitioning was tested with a join of Cus-
tomer, Orders, and LineItem. We tested the original
bit mapper with no hybrid component, an exact map-
per with a hybrid component, a bit mapper with a hy-
brid component, and HHJ. The bit mapper with no
hybrid component used its entire memory allocation
during partitioning for the bit mapper. The hybrid
bit mapper used 12 bytes * number of tuples in the
Orders relation as its bit map size which is the same
amount of space used by the exact mapper. The re-
sults are in Figure 8 (time) and Figure 9 (IOs).
For this join, the multi-way algorithms had fewer
I/Os but that did not always translate to a time ad-
vantage unless the difference was large. The hy-
brid stage is a major benefit as the join memory in-
creases. HHJ had worse performance on a memory
jump from 2000 MB to 2500 MB despite performing
20GB fewer I/Os! The difference was the optimizer
changed the query plan to join Orders with LineItem
then the result with Customer at 2500 MB where pre-
400
500
600
700
800
900
1000
1100
0 500 1000 1500 2000 2500 3000
Time (sec)
Memory Size (MB)
HHJ
N-way (exact,hybrid)
N-way (bitmap,no hybrid)
N-way (bitmap,hybrid)
Figure 8: Customer-Orders-LineItem (Time).
0
5000
10000
15000
20000
25000
30000
35000
0 500 1000 1500 2000 2500 3000
I/Os (MB)
Memory Size (MB)
HHJ
N-way (exact,hybrid)
N-way (bitmap,no hybrid)
N-way (bitmap,hybrid)
Figure 9: Customer-Orders-LineItem (I/O bytes).
viously Customer and Orders were joined first. This
new ordering produced double the number of probes
and join clause evaluations and ended up being slower
overall.
The major limitation was the mapper size. The
mappers did not produce results for the smaller mem-
ory sizes of 32 MB and 64 MB as the mapper could
not be memory-resident. For 128 MB, the bit map-
per performed significantly more I/Os and had larger
time than the exact mapper due to the number of false
drops. The number of false drops was greatly reduced
as the memory increased. The bit mapper without
a hybrid component continued to read/write all rela-
tions and was never faster than HHJ.
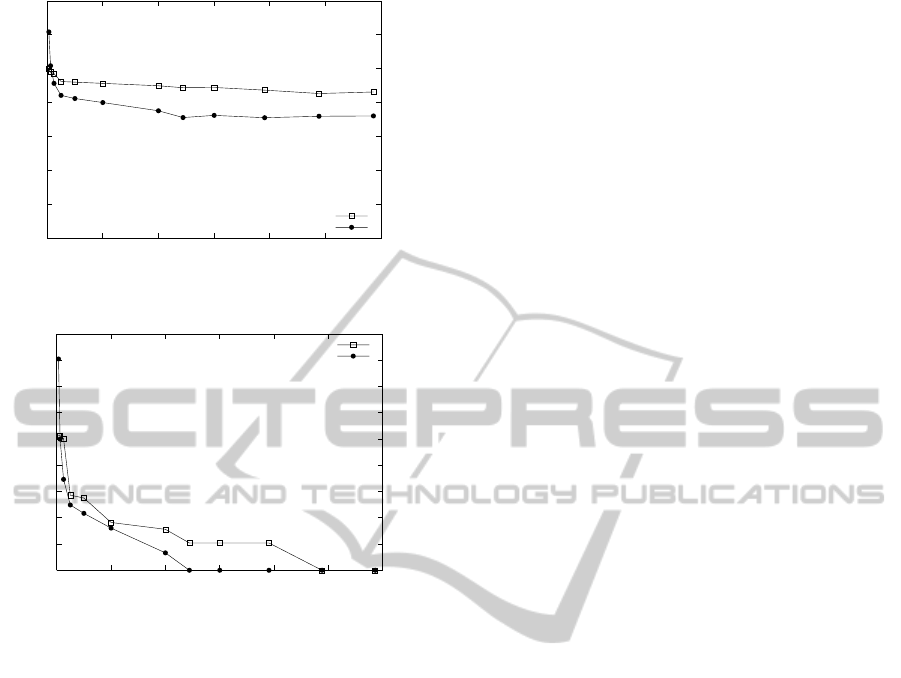
6.3 Multi-Dimensional Partitioning
One of the star join tests combined Part, Orders,
and LineItem. The performance of the SHARP algo-
rithm versus hybrid hash join is in Figures 10 and 11.
SHARP performed 50-100% fewer I/Os in bytes and
was about 5-30% faster. Only at very small memory
sizes did the performance become slower than HHJ,
and it was faster in the full memory case.
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
20

0
200
400
600
800
1000
1200
1400
0 500 1000 1500 2000 2500 3000
Time (sec)
Memory Size (MB)
HHJ
N-way (multi)
Figure 10: Part-Orders-LineItem (time).
0
10000
20000
30000
40000
50000
60000
70000
80000
90000
0 500 1000 1500 2000 2500 3000
I/Os (MB)
Memory Size (MB)
HHJ
N-way (multi)
Figure 11: Part-Orders-LineItem (I/O bytes).
6.4 Results Discussion
Multi-way joins can be added to the optimizer using
post-optimization. Post-optimization has a low bar-
rier to entry and catches many of the opportunities for
exploiting multi-way joins. The cost functions allow
the optimizer to choose between the binary and multi-
way operators.
Implementing efficient, robust, and scalable
multi-way joins is a non-trivial challenge. The ex-
perimental results clearly show that multi-way perfor-
mance depends on the join type. Direct partitioning
joins are efficient and are clearly superior when the
hash attributes uniquely identify tuples in each input.
However in that case, it is also likely that interesting
orders based on sorting may apply (as the relations
may be sorted on the primary/unique attribute) which
would have even better performance. Direct partition-
ing joins where a tuple in one input may match with
many in the other inputs has better performance in
some cases primarily due to sharing memory over all
inputs, but despite numerous optimizations, we have
been unable to demonstrate improved performance
over all memory sizes, especially smaller memory
sizes. Lazy materialization is superior to eager mate-
rialization as it saves both memory and I/Os for mate-
rializing intermediate results and also the time to con-
struct and probe them in intermediate hash tables.
Indirect partitioning has benefits, but the mapping
functions consume both space and CPU time. Indi-
rect partitioning is inapplicable if the mappers can-
not be completely memory-resident during partition-
ing. Indirect partitioning without a hybrid step is not
competitive with binary plans. Note that this does
not contradict the results in (Kemper et al., 1999)
as the join algorithm was not used in conjunction
with the space saving hash aggregation structure pro-
posed. The results clearly show both a benefit and
an issue with direct and indirect partitioning joins.
The number of I/Os performed is less but that does
not always translate into a time advantage. The I/O
cost is often reduced by intelligent operating system
buffering. Overall, indirect partitioning joins are not
as robust as binary joins and the high CPU cost of-
ten outweighs any I/O advantages. Similar to main-
memory optimized joins, optimizing algorithms for
cache-awareness is very beneficial for performance.
A cache-aware multi-way join may have even better
performance.
Multi-dimensional partitioning as implemented in
SHARP is a much more consistent winner. The major
bad case relates to the “curse of dimensionality” when
build inputs are read multiple times and more I/Os are
performed than the corresponding binary plan. This
case is identified by the cost functions and will be
avoided by the optimizer. Like the one-to-one di-
rect partitioning joins, multi-way partitioning is faster
than binary plans for the fully in-memory case. This
speed improvement occurs as it does not material-
ize intermediate results and performs the same (or
fewer) number of probes than binary plans. Further,
star queries are much more common than the types of
queries that would be beneficial for direct or indirect
partitioning. Multi-dimensional partitioning is a ben-
eficial addition to the set of join operators and in its
most basic implementation (without any adaptability)
is fairly straightforward to implement.
7 CONCLUSIONS
The goal of this paper was to determine if multi-way
joins are useful in a database system. The answer is
yes, especially for star queries. Direct and indirect
partitioning multi-way joins improve performance in
some cases, especially for one-to-one joins. The
two major issues are the relatively limited number of
queries affected, and the care that must be taken to
guarantee good performance. Multi-dimensional par-
AreMulti-wayJoinsActuallyUseful?
21

titioning is beneficial for a larger number of queries,
more efficient except for known cases, and more
stable to implement. Multi-dimensional partitioning
joins should be implemented in commercial database
systems.
Future work includes allowing the optimizer to
cost multi-way joins simultaneously with binary plans
and conducting experiments to evaluate multi-way
joins in conjunction with aggregation operators.
REFERENCES
Afrati, F. N. and Ullman, J. D. (2011). Optimizing Mul-
tiway Joins in a Map-Reduce Environment. IEEE
Trans. Knowl. Data Eng., 23(9):1282–1298.
Albutiu, M.-C., Kemper, A., and Neumann, T. (2012).
Massively Parallel Sort-Merge Joins in Main Memory
Multi-Core Database Systems. PVLDB, 5(10):1064–
1075.
Bizarro, P. and DeWitt, D. J. (2006). Adaptive and Ro-
bust Query Processing with SHARP. Technical Re-
port Technical Report 1562, University of Wisconsin.
Blanas, S., Li, Y., and Patel, J. M. (2011). Design and evalu-
ation of main memory hash join algorithms for multi-
core CPUs. In SIGMOD Conference, pages 37–48.
Chaudhuri, S. and Narasayya, V. TPC-D data gen-
eration with skew. Technical report, Microsoft
Research, Available at: ftp.research.microsoft.com/
users/viveknar/tpcdskew.
DeWitt, D., Katz, R., Olken, F., Shapiro, L., Stonebraker,
M., and Wood, D. (1984). Implementation Techniques
for Main Memory Database Systems. In ACM SIG-
MOD, pages 1–8.
DeWitt, D. and Naughton, J. (1995). Dynamic Memory Hy-
brid Hash Join. Technical report, University of Wis-
consin.
Graefe, G. (1992). Five Performance Enhancements for
Hybrid Hash Join. Technical Report CU-CS-606-92,
University of Colorado at Boulder.
Graefe, G., Bunker, R., and Cooper, S. (1998a). Hash Joins
and Hash Teams in Microsoft SQL Server. In VLDB,
pages 86–97.
Graefe, G., Ewel, J., and Galindo-Legaria, C. (Septem-
ber 1998b). Microsoft SQL Server 7.0 Query
Processor at msdn.microsoft.com/en-us/library/
aa226170(SQL.70).aspx. Technical report, Microsoft
Corporation.
Kemper, A., Kossmann, D., and Wiesner, C. (1999). Gener-
alised Hash Teams for Join and Group-by. In VLDB,
pages 30–41.
Kitsuregawa, M., Nakayama, M., and Takagi, M. (1989).
The Effect of Bucket Size Tuning in the Dynamic Hy-
brid GRACE Hash Join Method. In VLDB, pages 257–
266.
Lawrence, R. (2008). Using Slice Join for Efficient Evalu-
ation of Multi-Way Joins. Data and Knowledge Engi-
neering, 67(1):118–139.
Microsoft Corporation (May 2001). Description of Ser-
vice Pack 1 for SQL Server 2000 at http://support.
microsoft.com/kb/889553. Technical report, Microsoft
Corporation.
Moerkotte, G. and Neumann, T. (2008). Dynamic program-
ming strikes back. In ACM SIGMOD, pages 539–552.
Nakayama, M., Kitsuregawa, M., and Takagi, M. (1988).
Hash-partitioned join method using dynamic destag-
ing strategy. In VLDB, pages 468–478.
TPC (2013). TPC-H Benchmark. Technical report, Trans-
action Processing Performance Council.
Viglas, S., Naughton, J., and Burger, J. (2003). Maximiz-
ing the Output Rate of Multi-Way Join Queries over
Streaming Information Sources. In VLDB, pages 285–
296.
Walton, C. B., Dale, A. G., and Jenevein, R. M. (1991).
A Taxonomy and Performance Model of Data Skew
Effects in Parallel Joins. In VLDB, pages 537–548.
Zhang, X., Chen, L., and Wang, M. (2012). Efficient
Multi-way Theta-Join Processing Using MapReduce.
PVLDB, 5(11):1184–1195.
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
22